Genetic Algorithm Visualization and INterataction (GAVIN)

Gregory S. Hornby hornby@cs.brandeis.edu Dynamic & Evolutionary Machine Organization Lab

First I should mention what my thesis is. It is not uncommon for people to implement a GA on a parallel machine. Usually the performance of these parallel implementations are comparable with a simple, sequential GA. Sometimes the parallel GA will achieve super-linear speedup. I am investigating whether imposing a structure on the population can improve the performance of a GA on some classes of functions.

A tool for understanding Genetic/Evolutionary Algorithms

G.A.V.IN. is a research tool I built with some assistance from my friend Paul. It stands for Genetic Algorithm Visualization and INteraction. There are two parts to the program, the genetic algorithm library and the graphics library. I wrote the GA part and Paul wrote most of the graphics part.

For those who are interested there is a chapter and an appendix on GAVIN in my MSc thesis.

I am studying the search properties of parallel genetic algorithms. The two main models I am looking at are the Island Model and the Neighbourhood Model. The first has a number of subpopulations, each containing a number of individuals. Each subpopulation runs like a canonical GA with some communication (exchange of individuals) between subpopulations. The second model has each individual located on some topography (eg a grid) with the restriction that it is only allowed to communicate (reproduce) with its immediate neighbours.

Here are some pictures from a sample run. The first picture shows the population (red cubes) at an early generation, the second picture shows the population near the end of the run.

A Sample Run

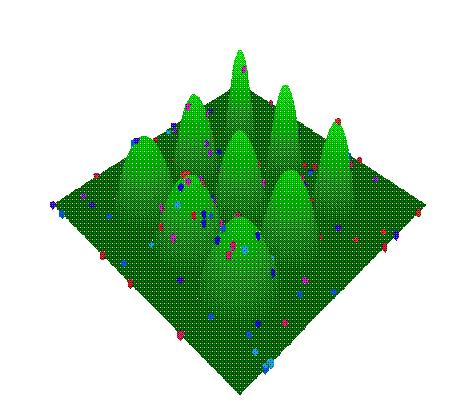The initial population.	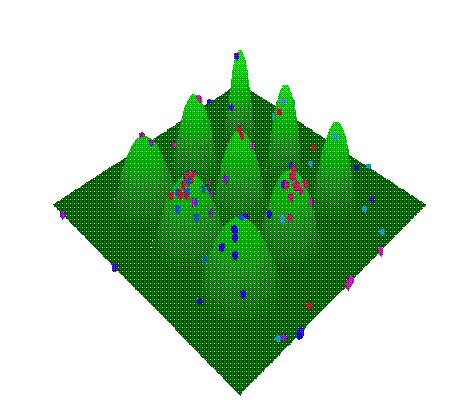The population after 9 generations.
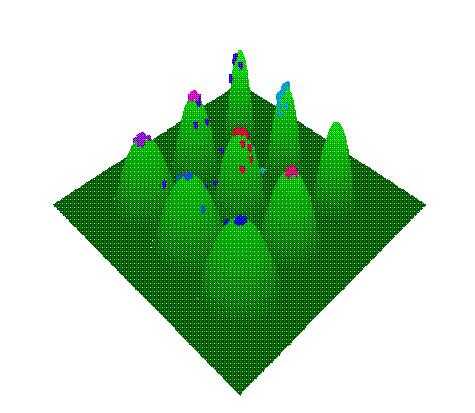The population after 19 generations.	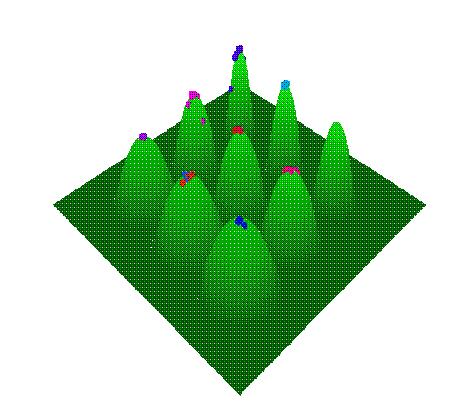The population after 30 generations.

The significance of this finding is that it shows that a population's conver gence properties can be controlled by the structure of the population. One problem that plagues EAs is premature convergence, the conver gence of the population to a sub-optimal part of the fitness landscape. Using multiple sub-populations is a promising direction to go to alleviate this problem.

Findings

When individuals are paired up to produce offspring the offspring are created by applying the recombination operator with two parent individ uals as input and one or two offspring individuals as output. The find ings of studying recombination were that information about the fitness landscape must be incorporated into the operator for better than random search performance to be achieved.

In a 1932 paper, Sewall Wright proposed a theory for why semi-isolated sub-populations search a landscape better than one large population. Ac cording to his theory each sub-population drifts to different parts of the local landscape. Eventually one sub-population moves, by chance, onto a higher local optima. Through migration this more fit sub-population draws the other sub-populations to this part of the landscape and then the process repeats. Semi-isolated sub-populations are a diverse, mobile population. In contrast a single, large population converges to one peak and is hard to move. Results from studying EAs with different popula tion structures have shown that it does cause the EA to search in different ways.

Thanks and Acknowledgements

• Paul Ferry, for writing most of the graphics routines;
• Hong Zhang, for giving me access to the SGI in the Robotics lab;
• and the Graphics Group for letting me use the SGIs in their lab.

Publications