Sorting Networks and the END search algorithm
An oblivious comparison-based algorithm is such that the sequence of
comparisons performed is the same for all inputs of any given size. This kind
of algorithm has received much attention since it admits an implementation
as circuits: comparison-swap can be hard-wired. Such an oblivious
comparison-based algorithm for sorting n values is called an
n-input sorting network (a survey of sorting network research
is in [1]).
There is a convenient graphical representation of sorting networks.
An horizontal line represents each input of the sorting network and
a connection between two lines represents each comparator which
compares the two elements and exchanges them if the one on the upper line is
larger than the one on the lower line.
The input of the sorting network is on the left of the representation.
Elements at the output are sorted and the largest element migrates to the
bottom line.
Performance of a sorting network can be measured in two different ways:
- Its depth which is defined as the number of parallel steps that
it takes to sort any input, given that in one step disjoint comparison-swap
operations can take place simultaneously. Current upper and lower bounds
are presented in the following table.
| Nb inputs |
1 | 2 | 3 | 4 | 5 |
6 | 7 | 8 |
9 | 10 | 11 | 12 | 13 |
14 | 15 | 16 |
| Upper bound |
0 | 1 | 3 | 3 | 5 |
5 | 6 | 6 |
7 | 7 | 8 | 8 | 9 |
9 | 9 | 9 |
| Lower bound |
0 | 1 | 3 | 3 | 5 |
5 | 6 | 6 |
7 | 7 | 7 | 7 | 7 |
7 | 7 | 7 |
- Its length, that is the number of comparison-swap used.
Optimal sorting networks for n <= 8 are known exactly and are
presented in [1] along with the most efficient sorting networks
to date for 9 <= n <= 16. These results are presented in the following
table.
| Nb inputs |
1 | 2 | 3 | 4 | 5 |
6 | 7 | 8 |
9 | 10 | 11 | 12 | 13 |
14 | 15 | 16 |
| Comparators |
0 | 1 | 3 | 5 | 9 |
12 | 16 | 19 |
25 | 29 | 35 | 39 |
|
51 | 56 | 60 |
() Before the END algorithm improved this upper bound,
the best known upper bound for the 13-input sorting network
was 46.
The 16-input sorting network has been the most challenging one.
Knuth [1] recounts its history as follows.
First, in 1962, Bose and Nelson discovered a method for constructing sorting
networks that used 65 comparisons and conjectured that it was best possible.
Two years later, Floyd and Knuth, and independently Batcher, found a new method
and designed a sorting network using 63 comparisons.
Then, a 62-comparator sorting network was found by Shapiro in 1969, soon to
be followed by Green's 60 comparator network, presented below.
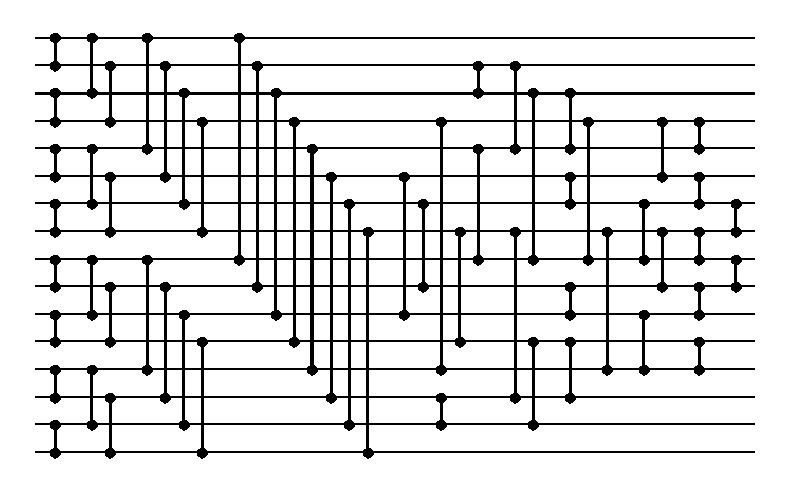
Green's contruction: 60-comparator 10 parallel steps 16-input sorting network.
Until recently, none of the upper bounds presented in [1] has been
improved, neither Green's optimal construction for a 16-input sorting network
has been reproduced!
A famous work after Hillis [2], addressed the problem of finding optimal
sorting networks (regarding the number of comparators) in the case of 16 inputs.
Hillis used a simulated evolution approach and got impressive results, given
the difficulty of the problem.
Moreover, his work addressed some innovative issues for search algorithms, like
the use of co-evolution.
However, he hasn't been able to achieve the best known upper bound and discovered
only a 61-comparator solution, presented below.
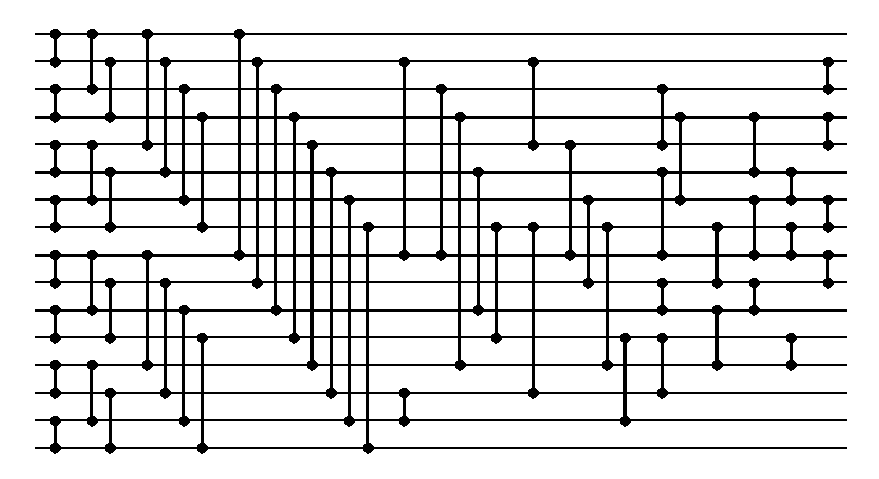
Hillis' construction (co-evolving parasites): 61-comparator 11 parallel steps
16-input sorting network.
Moreover, Hillis introduced an important bias in his search algorithm by
initializing the population with the first 32 comparators of the best known
construction. The search was limited around this local optimum and, thus, the
final solution still used these initial 32 comparators.
The Evolving Non-Determinism (END) search algorithm
The END algorithm can be seen as a massively parallel search algorithm
for which elements of the population interact locally.
Simulated evolution is used as the paradigm that focus the search
in the state space.
This approach provided impressive results, in particular for the sorting
network problem.
Compared to Hillis' work, shorter sorting networks were discovered without
any initial condition.
Even a 25-year old result for the upper bound on the number of comparators
for the 13-input case has been improved by one comparator!
The paper presenting the END algorithm can be downloaded by
clicking here.
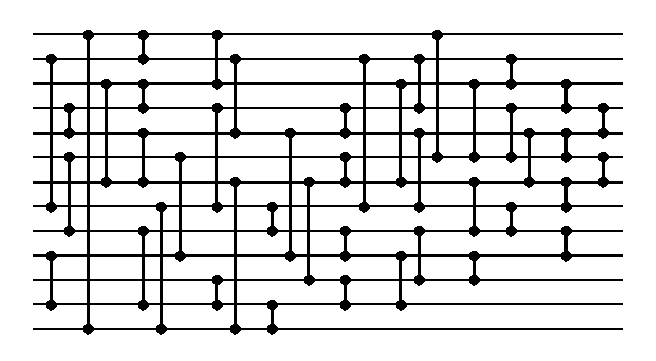
Some of these sorting networks discovered by END are presented below.

END algorithm: 60-comparator 10 parallel steps 16-input sorting network.
END algorithm: 45-comparator 10 parallel steps 13-input sorting network.
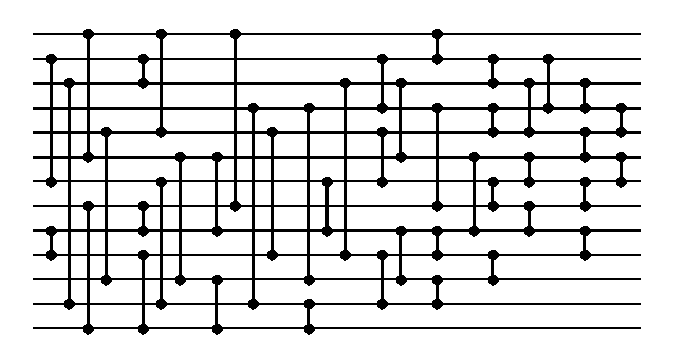
END algorithm: 45-comparator 10 parallel steps 13-input sorting network.
[1] Knuth, D. E. (1973). The Art of Computer Programming, volume 3:
Sorting and Searching. Addison Wesley.
[2] Hillis, W. D. (1992). Co-evolving parasites improve simulated evolution
as an optimization procedure. In Langton, C. et al. (Eds.),
Artificial Life II. Addison Wesley.



