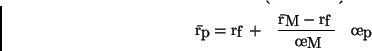

Next: Portfolio Management and Information
Up: CAPM
Previous: Separation Theorem
From the Separation Theorem we can see that in equilibrium, every security must be part of the investor's risky portion of the portfolio. The reason is that if a security isn't in T, no one is investing in it, meaning that its prices will fall, causing the expected returns of it to rise until the resulting tangency portfolio has a nonzero proportion associated with them.
When all the price adjusting stops, the market will have been brought into equilibrium.
- Each investor will want to hold a certain positive amount of each risky security.
- The current market price of each security will be at a level where the number of shares demanded equals the number of shares outstanding.
- The riskfree rate will be at a level where the total amount of money borrowed equals the total amount of money lent.
This gives rise to the following definition of the market portfolio:
Definition 1
The market portfolio is a portfolio consisting of all securities where the proportion invested in each security correspons to its relative market value. The relative market value of a security is simply equal to the aggreagte market value of the security divided by the sum of the aggregate market values of all securities.
In equilibrium the proportions of the tangency portfolio will correspond to the proportions of the market portfolio. This tells us that the market portfolio plays a central role in the CAPM, since the efficient set consists of an investment in the market portfolio, coupled with a desired amount of either riskfree borrowing or lending.
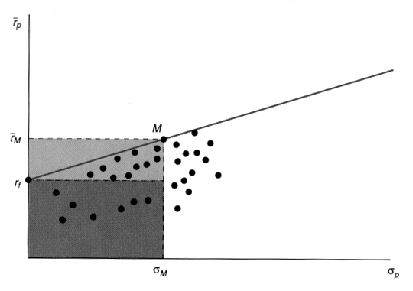
Figure:
The Capital Market Line. M is the market portfolio and rf represents the riskfree rate of return. All portfolios other than those employing the market portfolio and riskfree borrowing or lending would lie below the CML.
 |
The linear efficient set of the CAPM is known as the Capital Market Line, which has the following equation
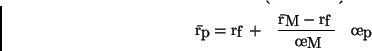 |
(1) |
where
We now know that using the CAPM we can decide whether the market price for a stock is too high or too low by looking at the market portfolio.


Next: Portfolio Management and Information
Up: CAPM
Previous: Separation Theorem
Magnus Bjornsson
1998-05-12