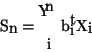Theorem 3
Assume that

are differentiable functions (satisfying certain regularity conditions.) Then
can be an optimal solution for the non-linear programming problem only if there exist
m numbers
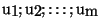
such that all the following KKT conditions are satisfied:
Theorem 4
The log-optimal portfolio
b* for a stock market
X (i.e., the portfolio that maximizes the doubling rate), satisfies the following necessary and sufficient conditions:
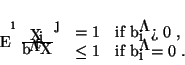 |
(7) |