

Next: The EPR paradox steps
Up: Heads or Tails? Quantum
Previous: ``Post-Cold War'' Cryptographic Scenarios
The BB84 QBC protocol by Bennett and Brassard [1] is quite similar
to the well-known BB84 QKD protocol:
- BB84 Quantum Bit Commitment Protocol2
- 1.
- Commitment Phase
- (a)
- A chooses her bit b and s random bits
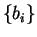 .
Then proceeds to send s particles to B, each one encoding biwith respect to the basis
.
Then proceeds to send s particles to B, each one encoding biwith respect to the basis
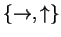 (if b=0)
or
(if b=0)
or
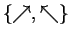 (if b=1)
(if b=1)
- (b)
- B chooses s random bits
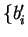 and measures the qubits
received with respect to the basis
and measures the qubits
received with respect to the basis
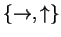 (when
(when
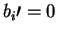 )
or
)
or
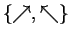 (when
(when
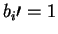 ).
).
- 2.
- Disclosure Phase
- (a)
- A reveals b and
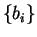 .
B verifies that bwas measured for all i such that
.
B verifies that bwas measured for all i such that
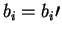 .
.
Table 1 enumerates the probabilities of measuring either 0 or 1
depending on the values of b, bi and
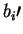 .
.
Here b is hidden in the basis, either horizontal or rotated by 45 degrees.
Alice is sending a mixture of orthogonal states to confuse Bob, who can not
tell whether is receiving mixed
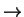 's and
's and  's
or mixed
's
or mixed 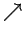 's and
's and 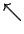 's. It all will make sense,
however, when the list of initial polarizations is sent: he will have measured
50% of the particles with the correct basis, providing a certain measure. If
any of those turns out to be incorrect, he will know that cheating was involved.
's. It all will make sense,
however, when the list of initial polarizations is sent: he will have measured
50% of the particles with the correct basis, providing a certain measure. If
any of those turns out to be incorrect, he will know that cheating was involved.
Before the disclosure takes place, B gains no information at all from
the protocol, as illustrated by table 1. He could try to cheat by
using any arbitrary basis, but whatever measurements he does, the randomness
of 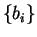 implies that he cannot guess the value of b before
the disclosure phase (table 2).
implies that he cannot guess the value of b before
the disclosure phase (table 2).
Due to the orthogonality of the measurement basis, we know that
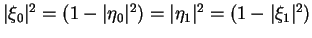 and also
and also
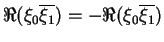 ,
so the probabilities of measuring 0 and 1 when bi=0 are reciprocal
to those obtained when bi=1. All put together, whatever measurement
B does, he gains no information on b without knowing bi3.
,
so the probabilities of measuring 0 and 1 when bi=0 are reciprocal
to those obtained when bi=1. All put together, whatever measurement
B does, he gains no information on b without knowing bi3.
When A reveals the list of 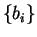 ,
B is able to confirm
that indeed all his measurements gave the right value for the approximately
,
B is able to confirm
that indeed all his measurements gave the right value for the approximately
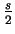 times that bi was equal to
times that bi was equal to
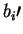 .
.
Also, A cannot cheat, for table 3 suggests that whatever
she sends will have a probability equal to
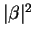 of being caught
if she tries to make believe it was a zero, and of
of being caught
if she tries to make believe it was a zero, and of
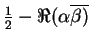 if she tries to make believe it was a one (when it happens to be measured with
the aligned basis). The only way to be certain that B will accept the
protocol is to either make
if she tries to make believe it was a one (when it happens to be measured with
the aligned basis). The only way to be certain that B will accept the
protocol is to either make
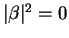 by sending
by sending
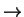 and committing to zero or make
and committing to zero or make
 by sending
by sending 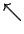 and committing to one.
and committing to one.
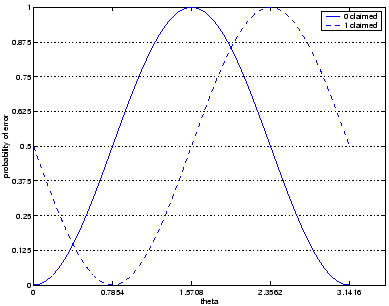
If A would be willing to take risks, she would face a situation as in
figure 2, where we have set
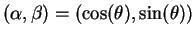 4. With
4. With
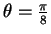 for example, the probability of error is
for example, the probability of error is
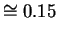 for both measurements, so A would not be caught with
a probability of
for both measurements, so A would not be caught with
a probability of
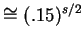 which rapidly approaches zero when
the protocol is done with a sufficiently large number s of iterations.
which rapidly approaches zero when
the protocol is done with a sufficiently large number s of iterations.
Figure 2:
Alice's chances of being caught, per qubit sent.
|
|
This protocol looks as secure as Quantum Key Distribution, at a first glance.
It does have a failure, however, as Bennett and Brassard realized from the beginning.


Next: The EPR paradox steps
Up: Heads or Tails? Quantum
Previous: ``Post-Cold War'' Cryptographic Scenarios
1999-11-04
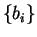 .
Then proceeds to send s particles to B, each one encoding biwith respect to the basis
.
Then proceeds to send s particles to B, each one encoding biwith respect to the basis
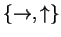 (if b=0)
or
(if b=0)
or
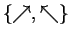 (if b=1)
(if b=1)
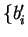 and measures the qubits
received with respect to the basis
and measures the qubits
received with respect to the basis
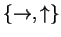 (when
(when
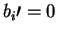 )
or
)
or
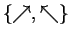 (when
(when
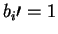 ).
).
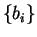 .
B verifies that bwas measured for all i such that
.
B verifies that bwas measured for all i such that
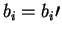 .
.
