

Next: The Quantum Computer bites
Up: Heads or Tails? Quantum
Previous: The EPR paradox steps
A number of papers were published that extended the original BB84 quantum bit
commitment protocol. Brassard and Crepéau suggested in 1991 the following protocol
to fix the problems with BB84 [4]:
- 1.
- Commitment Phase
- (a)
- Alice prepares s random bit strings, each one of length s. The
parity of each bit string should be equal to the committed bit, b. Each
string will be called
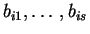 .
.
- (b)
- Alice encodes each bij with a random basis
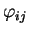 ,
either
,
either
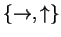 or
or
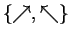 ,
and sends
to Bob. Bob measures each bit with respect to a randomly chosen basis
,
and sends
to Bob. Bob measures each bit with respect to a randomly chosen basis
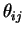 ,
either
,
either
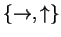 or
or
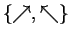 .
The results of these measurements will be called
.
The results of these measurements will be called
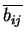 .
.
- 2.
- Disclosure Phase
- (a)
- Alice tells Bob what b was, and also sends all the values for
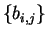 and
and
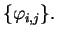
- (b)
- Bob verifies that
- i.
- The parity of all strings
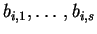 is indeed b
is indeed b - ii.
- Whenever it happened that
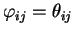 ,
the value bijsupposedly encoded is indeed equal to the observed
,
the value bijsupposedly encoded is indeed equal to the observed
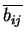 .
.
Brassard and Crépeau here thought that the EPR attack was nearly impossible
in practice, and that they were offering this improved version just for the
sake of completeness.
The rationale is that, unlike the earlier protocol, all bases and bits are random,
b being encoded in the parity. Alice cannot guess what the decoding bases
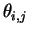 are, so, would she keep an entangled qubit for herself,
measuring it with the wrong basis would yield a 50% probability of error. The
authors claimed that this protocol was immune to the EPR attack but were not
sure about a higher-scale consequence of quantum physics: ``coherent measurements''.
Without explaining much, what they seem to fear is what ultimately would kill
the whole enterprise, namely, that the same kind of phenomenon that enabled
the EPR attack, the composite state of sets of two or more particles, applies
to the composite state of all the particles involved in the protocol.
are, so, would she keep an entangled qubit for herself,
measuring it with the wrong basis would yield a 50% probability of error. The
authors claimed that this protocol was immune to the EPR attack but were not
sure about a higher-scale consequence of quantum physics: ``coherent measurements''.
Without explaining much, what they seem to fear is what ultimately would kill
the whole enterprise, namely, that the same kind of phenomenon that enabled
the EPR attack, the composite state of sets of two or more particles, applies
to the composite state of all the particles involved in the protocol.
For a while, however, this was considered to be a sound protocol and the research
focused on adding error correction to it, because actual physical quantum transmission
channels were beginning to be built and all of them had error probabilities.
In 1993 a paper by Brassard, Crépeau, Jozsa and Langlois appeared, pompously
named ``A Quantum Bit Commitment Scheme Provably Unbreakable by both Parties''
[5] that explained in full detail an extension to BC91 incorporating
error correction.
I won't describe BCJL93 in detail here because the error correction protocol
makes equations difficult to follow. This paper contains a proof of security
([5], theorem 3.7) that turned out to be flawed. Crépeau made this
comment three years later ([8], page 197):
The part of the ``proof'' that goes wrong is the fact that A is committed
to a bit. The paper shows that A is unable to know at the same
time information to unveil the commitment as b=0 and as b=1 and
concludes that A cannot change her mind. The first part of the statement
is correct, but not the conclusion. As a matter of fact, the first part of the
statement is also true of the BB84 protocol and we know that it can be broken!


Next: The Quantum Computer bites
Up: Heads or Tails? Quantum
Previous: The EPR paradox steps
1999-11-04
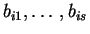 .
.
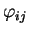 ,
either
,
either
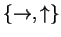 or
or
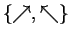 ,
and sends
to Bob. Bob measures each bit with respect to a randomly chosen basis
,
and sends
to Bob. Bob measures each bit with respect to a randomly chosen basis
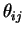 ,
either
,
either
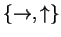 or
or
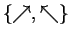 .
The results of these measurements will be called
.
The results of these measurements will be called
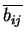 .
.
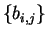 and
and
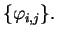
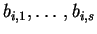 is indeed b
is indeed b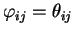 ,
the value bijsupposedly encoded is indeed equal to the observed
,
the value bijsupposedly encoded is indeed equal to the observed
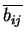 .
.