Next: Aftermath Up: Heads or Tails? Quantum Previous: Brassard, Crépeau, Jozsa, Langlois:

The Quantum Computer bites the Quantum Cryptographer

Three years passed before Lo and Chau, and Mayers discovered the flaws of BCJL93, more or less simultaneously. The advances in quantum computing theory provided them with better formalisms on quantum physics and quantum computations and allowed them to frame the problem with a clearer perspective. Their papers were first published online ([16], [11]) and later appeared together on Physical Review Letters ([17], [12]). To prove that quantum bit commitment is impossible, a general structure or scheme of a QBC protocol is needed, encompassing all possible such protocols. The authors at the time had doubts on the generality of the ones they had used. Lo and Chau's 1998 article [13] and review [7] have definitively settled the issue.⁶

The general idea of a protocol involves three quantum systems, one for Alice, one for Bob, and one for a communications channel. According to quantum physics, the state of each one of these is a unitary⁷ vector on a Hilbert⁸ space, so we must consider state spaces H_A, H_B, and H_Cfor each of this characters. The complete state of all of them put together is a vector in the direct (tensor) product of the three, namely the space $H_{A}\otimes H_{B}\otimes H_{C}$ . Note that in as much as quantum physics encompasses classical physics, this is also a description for any classical (or mixed) protocol. The protocol will require A and B to prepare and manipulate their states, which involves computing and storage. Once again, from the point of view of quantum physics, the most general description of these are quantum computers. The assumption is, then, that A and B have a quantum computer each. With this gadgets they are able to perform manipulations on their state-spaces, namely, to rotate the state by any unitary transformation⁹.

LC98 general Quantum Bit Commitment protocol

1.

Preparation of states.

(a): Alice chooses b. She sets H_A to one of two states specified by the protocol. Call them $\left\vert 0\right\rangle$ and $\left\vert 1\right\rangle$ . Thus Alice sets H_A to $\left\vert A_{initial}\right\rangle$ which is either $\left\vert 0\right\rangle$ or $\left\vert 1\right\rangle$ .
(b): Bob sets the initial states of both the communications channel and his side of the protocol. These initial states will be called $\left\vert C_{initial}\right\rangle$ and $\left\vert B_{initial}\right\rangle$ , respectively. So $H_{B}\otimes H_{C}=H_{BC}$ is set to state $\left\vert B_{initial}\right\rangle \otimes \left\vert C_{initial}\right\rangle$ = $\left\vert BC_{initial}\right\rangle$ .
(c): $\left\vert 0\right\rangle$ , $\left\vert 1\right\rangle$ and $\left\vert BC_{initial}\right\rangle$ are all specified by the protocol and known to both parties.

2.

Commitment.

(a)

Here Alice and Bob execute a commitment protocol. Each one of them, in turn, perform a unitary transformation involving their side and the communications channel. So Alice ``sees'' $H_{A}\otimes H_{C}$ whereas Bob acts on $H_{B}\otimes H_{C}$ . Each of these operations, of course, result in a unitary transformation of the whole state $H_{ABC}=H_{A}\otimes H_{B}\otimes H_{C}$ .
If we label this transformations U_A₁, U_B₁, ... ,U_{A_n}, U_{B_n} we conclude that the final state is¹⁰

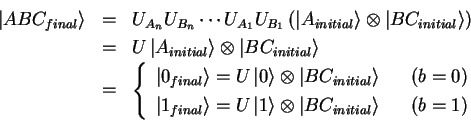
$\begin{displaymath}\begin{array}{rcl} \left\vert ABC_{final}\right\rangle & = & ... ...initial}\right\rangle & & (b=1) \end{array}\right. \end{array}\end{displaymath}$

3.

Disclosure

(a): Alice sends Bob all her quantum particles and Bob takes a measurement on the composite system which convinces him of what the commitment was.

After the commitment phase, the entire system is in one of two states: Either the state originating from an initial b=0, which will be called $\left\vert 0_{final}\right\rangle$ or the one generated from b=1, namely, $\left\vert 1_{final}\right\rangle$ . Since all the protocol is known to both parties, they both know the entire matrix U of the whole computation process, the only difference being that Bignores what the initial state of H_A was.

The key element at this point is that B must get no information whatsoever on what the value of b is. So both states $\left\vert 0_{final}\right\rangle$ and $\left\vert 1_{final}\right\rangle$ must look identical from his point of view. This said in mathematical terms, the trace with respect to H_Aof the observable associated with $\left\vert 0_{final}\right\rangle$ is identical to that of $\left\vert 1_{final}\right\rangle$ . We do this with a tool called Schmidt decomposition[7]: there are bases $\{e_{i}\}$ of H_Aand $\{\phi _{i}\}$ of H_BC , and numbers $\{\alpha _{i}\}$ such that

$\begin{displaymath}\left\vert 0_{final}\right\rangle =\sum \sqrt{\alpha _{i}}\le... ...t e_{i}\right\rangle \otimes \left\vert \phi _{i}\right\rangle \end{displaymath}$

and the trace taken to bring the observable $\left\vert 0_{final}\right\rangle \left\langle 0_{final}\right\vert$ down to H_BC yields¹¹

$\begin{displaymath}Tr_{H_{A}}\left( \left\vert 0_{final}\right\rangle \left\lang... ...\vert \phi _{i}\right\rangle \left\langle \phi _{i}\right\vert \end{displaymath}$

Similarly, there are bases $\{e_{i}\prime \}$ of H_A and $\{\phi _{i}\prime \}$ of H_BC, and scalars $\{\beta _{i}\}$ such that

$\begin{displaymath}\left\vert 1_{final}\right\rangle =\sum \sqrt{\beta _{i}}\lef... ...\right\rangle \otimes \left\vert \phi _{i}\prime \right\rangle \end{displaymath}$

and

$\begin{displaymath}Tr_{H_{A}}\left( \left\vert 1_{final}\right\rangle \left\lang... ...}\prime \right\rangle \left\langle \phi _{i}\prime \right\vert \end{displaymath}$

But since B cannot tell between each other, it must be the case that for all i, $\alpha _{i}=\beta _{i}$ and $\phi _{i}=\phi _{i}\prime$ . The only difference between the states lies inside H_A which means now that A can manipulate it at will! This is the problem that ruins the whole setup. Alice does not need to have access to H_BC in order to cheat. Here's what she should do:

Alice cheats with a quantum computer

1.: Prepare $\left\vert 0\right\rangle$ as if she were committing to the bit 0.
2.: Go over the protocol with B.
3.: When the time comes to open the commitment, if she wishes it to be zero, does nothing. Otherwise uses her quantum computer to apply the basis change operator $C(\{e_{i}\},\{e_{i}\prime \})$ on H_A. Now when B does his measurement, the state is $\left\vert 1_{final}\right\rangle$ and he is convinced that Alice was committed to 1 all along.

Perhaps all this quantum mathematical symbols were not even necessary. Suffice to say that, according to quantum mechanics, and according to Mayers, Lo and Chau, the two requirements for a bit commitment, which are that Bob cannot get early information, and that Alice can't cheat, are mutually exclusive because both ``committed'' states must be identical from Bob's point of view, so if Alice has the means, such as quantum storage and quantum computers, she can modify things up to the last minute.

Next: Aftermath Up: Heads or Tails? Quantum Previous: Brassard, Crépeau, Jozsa, Langlois:

1999-11-04