Emergent behaviors are difficult to quantify: how could we measure ``wandering''
? In this section we examine some behaviors that we were able to define with
simple formulas, allowing us to count their occurrences quickly by using regular
expressions.
|
Two consecutive turns of a Tron player can be either in the same direction (left-left or right-right) or in opposite directions (right-left or left-right). The former are U moves, and the latter S moves. The size of the move is the number of pixels advanced between the two turns. Most of the different behaviors we quantified are formally defined by a regular expression on the sequence of turns thus defined (table 3.4).
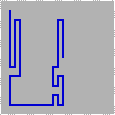1.
Tight Turns A tight turn is defined as two consecutive turns to the
same side, within 6 steps of each other (U<6). The icon depicts a player
doing 8 tight U turns.
2.
Spirals A spiral can be outwards or inwards; it is characterized as making
four turns in the same direction.
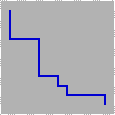3.
Staircase A staircase is defined as 4 consecutive alternating turns.
4.
Zig-zag A player is ``zig-zagging'' when alternating left-left then
right-right turns.
5.
Looping A player ``loops'' around the torus when she goes straight for
more than 150 steps, then makes a quick `S' turn (less than 14 steps) to make
a second pass parallel to the first one (fig. 3.29 left).
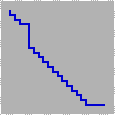6.
Diagonal A diagonal move is a tight staircase, all turns within 15 steps
of each other (fig. 3.30).
7.
Zig-zag filling This behavior is a combination of zig-zag and tight turns;
a succession of 2 opposite tight U turns. It is a useful strategy to fill up
the space tightly. The human player on fig. 3.36 spent most of the
match executing this behavior.
8.
Turns Some players go straight for a long time, others are turning all
the time. This feature could also be called ``nervousness''.
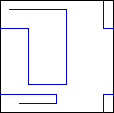9.
Asymmetry Some players prefer to do mostly left turns or right turns; others
have a 50%-50% balance. According to the definition on table 3.3,
an asymmetry equal to one means all turns have been made to the same side, and
a zero asymmetry means an equal number of turns to both sides. The icon depicts
a player making seven right turns but just one left turn (6/8 asymmetry = 0.75).
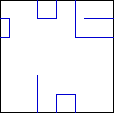10.
Edge Crossing Each time a player crosses the edge of the screen, to reappear
on the opposite side. Agents do this without noticing, since they have no perception
of the arena having edges; they just see a continuous topology. Humans need
to learn to mentally connect the opposite borders of the screen. The icon depicts
a player going across the edge five times.
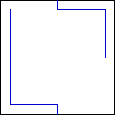11.
Edging Each step a player runs parallel to the edge of the screen within
10 pixels of it (see fig. 3.35).
12.
Spiral in and Out We have observed that one of the ways Tron agents may
use to gain a space and exploit it, is a spiral that goes in first, then out.
This player can spiral in loosely, then go backwards, spiraling out. The pure
spiral behavior often ends in a crash (fig. 3.28) but after spiraling
in, then out, the player is still alive. The agent of fig. 3.36
used this strategy at the upper right corner of the arena. We have defined it
as four consecutive turns to one side (spiral) followed by four turns to the
opposite side (opposite spiral).
The first question we wish to quantify is: Are any of these simple behaviors
being favored or disfavored by evolution? Is our system consistently relying
on any of them? The first group of results, fig. 3.38, shows the
frequency of behaviors along the history of the system. We grouped all games
in bins of 1000, and counted the occurrences of each of the 12 patterns, divided
by the number of steps. So each behavior is quantified as the ``propensity''
of the Tron system to engage in it (except for asymmetry which is a per-turn
ratio, not per-step).
|
|
The behaviors that occur with increased frequency along time are tight turns, zig-zags, filling zig-zags, edge following and spiral-in-out. Decreasing in frequency are spiraling and asymmetry. The others do not show a clear tendency. This confirms some of our intuitions, such as filling spaces and edging being favored by evolution. Spiraling on the other hand, is surprisingly disfavored. We must conclude that spiraling is a bad idea in general, albeit a necessary tool for a behavior that is a specialization of spiral -- spiral-in-then-out, which is favored by evolution.
The next question is, are these behaviors associated with a robot's measured
strength? Do some behaviors occur more or less often in stronger robots? The
associations should not be much different from those defined by time, since
performance is being selected across the time dimension. To observe this, we
have selected all robots whose accumulated games are at least 10000 steps, and
measured their behavioral frequency. On fig. 3.40 we have marked
one point per robot; the x coordinate being the strength, the y
coordinate the behavioral frequency. The result is a cloud of points, quite
disperse in all cases. This means that none of these behaviors implies, by itself,
that an agent is strong or weak. Quite the opposite, for each behavior one can
usually find both good and bad players who perform it either often or rarely.
|
|
The clouds of points do show some accumulation regions though, so we also divided the RS axis in six segments and calculated the mean and its standard error. We confirm with this that, on average, better robots are doing more tight turns, zig-zags, filling zig-zags and spirals in/out but less spirals -- and tend to have symmetrical behaviors and follow the edges of the screen.
![\( (\{U\vert S]\}>150)(S<14) \)](img260.gif){kind=small}
10 and parallel to edge
