Networks of Torque Propagation

  

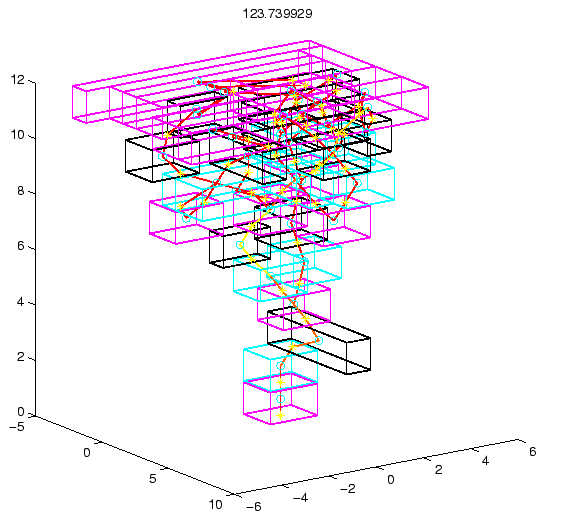
Figure 2.4:3D Lego structure generated by our evolutionary process. The underlying physical model is shown.

Our model for a 2D structure of bricks generates a network, called a Network of Torque Propagation (NTP) consisting of nodes, joints and loads.

• Each node represents a brick and its located at the brick's center of mass (circles in our figures).
• An additional node represents the ground.
• Each pair of locked bricks gives raise to a joint. The joint has an origin node, a destination node, an axis of rotation (located at the center of the area of contact between the bricks) and a maximum torque capacity (depending on the number of knobs involved). Joints are represented by lines in our figures, their axis of rotation by stars.
• Loads represent the forces acting on the network. Each has magnitude, direction, point of application, and entry node. For each brick, a force corresponding to its weight originates at the center of mass, is applied at the corresponding node, and points downwards. External forces may have any direction and their point of application is not necessarily the center of the brick.

Each force, either the weight of one of the bricks or an external load, has to be absorbed by the joints in the structure and transmitted to the ground. The magnitude of the torque exerted by each joint j must lie in the interval [-K_j, K_j], where K_j represents its maximum capacity as deduced from table 2.1.

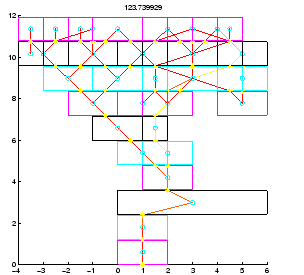
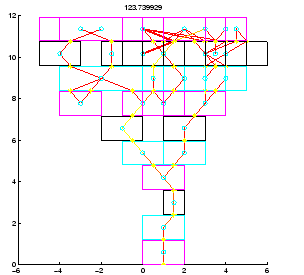
By separating each 3D joint into two orthogonal and independent 2D joints, which receive the x and y components of each force, we can project an entire 3D network model of a brick structure into two orthogonal planes, xz and yz, generating two 2D NTP's that can be solved separately (figs. 2.4 and 2.5). Thus the problem of solving a 3D network is reduced to that of solving 2D networks.

  

Figure 2.5: Projecting the 3D structure of fig. 2.4 to the xz and yz planes, two 2D networks are obtained that can be solved independently.