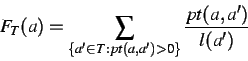Novelty Engine

Evolutionary algorithms create new entities and evaluate their fitness, introducing variations on the existing population through the use of crossover andmutation operators. Such recombinations often yield uninteresting individuals, identical to or worse than their parents. Typically, evaluations are rapid and unfit children are quickly filtered out. However, in our case, this approach would be wasteful since evaluation is obtained from a sparse resource -- precious interactions between agents and humans.

The Tron architecture uses a separate novelty engine as the source of new individuals. This module coevolves a population of 1000 agents by playing them against each other. The best robots are chosen to be incorporated into the main population. Even though self-play does not provide enough information to know which strategies will perform best against people, this method is much better than blind recombination for creating interesting new agents.

The novelty engine is a continuously running generational GA with 50% elitism. Every agent in the population plays against a training set T of t=25robots. Fitness is evaluated, and the bottom half of the population is replaced by random mating with crossover of the best half. The fitness function is defined as follows:

$$F_{T}(a)=\sum _{\{a'\in T:pt(a,a')>0\}}\frac{pt(a,a')}{l(a')}$$ (3.2)

where T is the training set, pt(a, a') = {0 if a loses against a', 0.5 if they tie and 1 if a wins} and l(a') is the number of games lost by a'. Thus we give more points for defeating good players than bad players.

The training set consists of two parts. There are f fixed members which come from the foreground process. The remaining t-f members of the training set are replaced each generation with a fitness sharing criteria. The new training set T' is initialized to the empty set and then new members are added one at a time, choosing the highest according to the following shared fitness function:

$$F_{T,T'}(a)=\sum _{a'\in T}\frac{pt(a,a')}{(1+\sum _{a''\in T}pt(a'',a)}$$ (3.3)

This selection function, adapted from Rosin [118], decreases the relevance of a case that has already been ``covered'', that is, when there is already a player in the training set that beats it.

At the end of a generation, the bottom half of the population is dropped, and so is the (changing) part of the training set. 500 new agents are created by (uniform) random mating (crossover), with a mutation rate of 0.04 (a parent's subexpression has a 4% chance of being replaced by a random new expression instead).