Given a single still image, we have considered the task of generating a plausible video from that image. Our target application is natural background with content such as trees, water, sky, clouds, etc. upon which foreground material may be superimposed. Potential applications range from low cost digital animation for movies and games, to video compression, to data augmentation for machine learning. We combine recently developed machine learning teachings for flows (e.g. A. Holynski et al. [2021] "Animating pictures with eulerian motion fields") with our previous work for oscillations for a multi-modal image animator which can handle constant flows and oscillations simultaneously. In our training pipeline, input images are directed to one of two generators (labeled G1 and G2) based on the nature of the motion contained in the corresponding video. In our inference pipeline, a still image is passed into each of our two motion predictors (predicted constant flow is then integrated over time). In our dataset generation pipeline, optical flow images (upper right) are generated by passing adjacent pairs of input frames into a pre-trained model. Below are three sample still images for which the resulting video looks plausible (click on one to play the corresponding video, and click again for full size).


We have developed a technique for low bitrate two-layer sprite encoding and decoding of videos with semantically salient foregrounds and dynamic background motion, such as an outdoor sports game. By representing the background motion using static descriptors, our technique improves visual quality in the video background while preserving the fidelity of semantically important foreground regions, and it can target lower bitrates than may be appropriate for codecs such as AVC and HEVC. In our two level video encoder pipeline, using machine learning foreground regions are separated and compressed using a standard codec with image persistence.
Masks are spatially downsampled and compressed with a standard codec. Background regions are filtered and reduced to a static sprite, complex valued modes of horizontal and vertical motion, and frame-wide global motion parameters. Here are sample frames from three versions of a 1 minute 48 seconds 1080p video, 59.94 fps, a total of 5868 frames; the top video was encoded with AVC at original quality (397,928,297 bytes, 0.26 bpp, approximately 29 Mbit/s), the middle is the same frame encoded by AVC at low quality settings (3,438,857 bytes, 0.0023 bpp, approximately 255 Kbit/s), and the bottom is the same frame encoded with our method (3,436,422 bytes or .0023 bpp, approximately 255 Kbit/s). The right two columns show closeups of the visual quality achieved. Note that AVC was used here for comparison because our HEVC tool could not be set to rates this low.

Here is a still frame from a soccer video (left), the video compressed by HEVC (middle), and our method (right); click and click again to enlarge.

Here is a frame taken from the same static soccer video (left) and the corresponding foreground mask generated by Mask R-CNN (right).

Here are three sample frames from our compressed simulated camera pan video of the same soccer game. On the left is shown the position of the frame on the warped background sprite, and on the right is our decoded frame.

A description of this work has been submitted for publication; here is a reference to a poster summary:
- S. Garber, R. Marcus, A. DiLillo, and J. A. Storer [2020]. "Low Rate Compression of Video with Dynamic Backgrounds", IEEE Data Compression Conference (DCC) 2020.
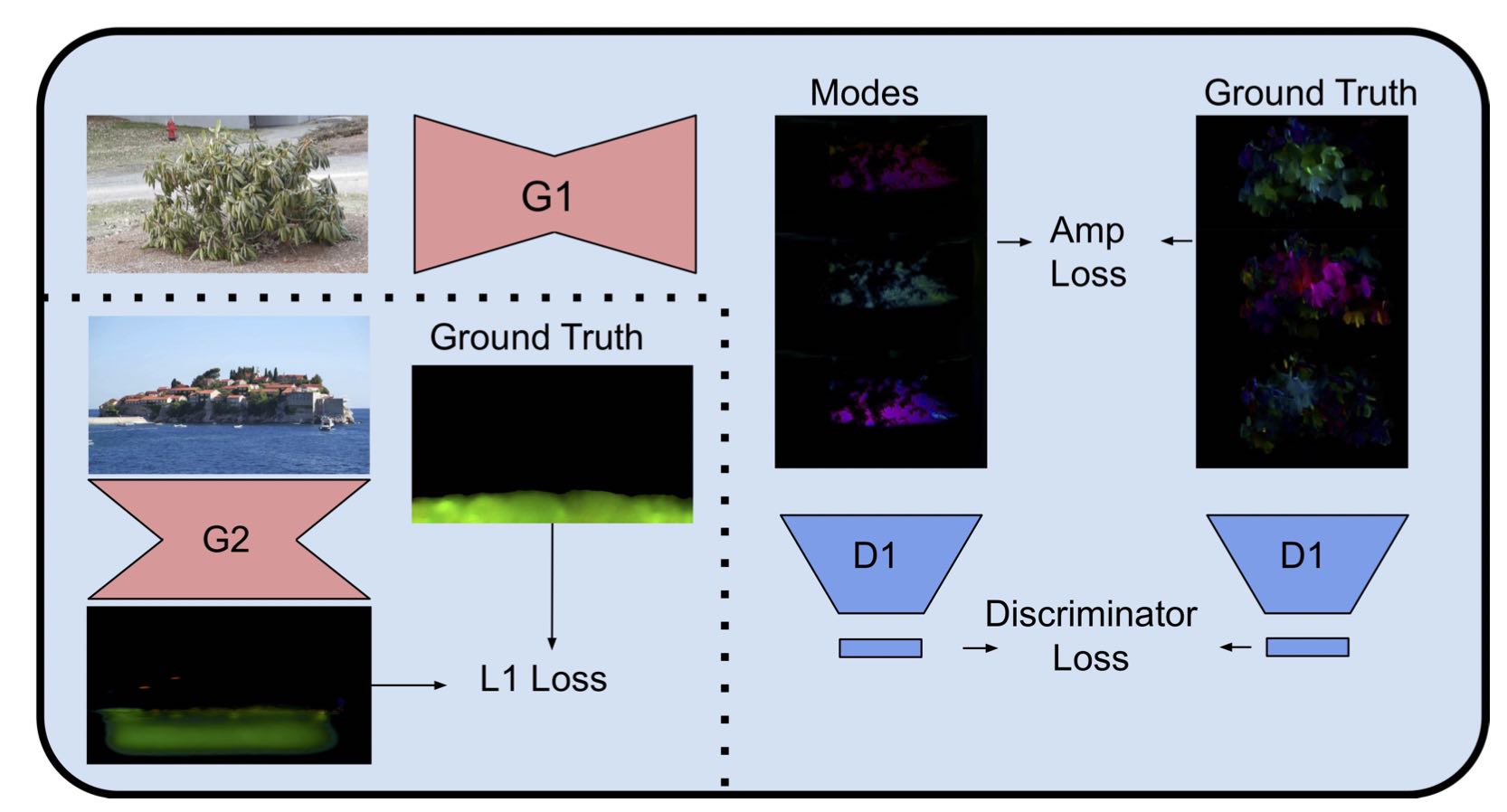
We have extended the idea of sprite coding to videos containing a wide variety of naturally occurring background motion, which could potentially be incorporated into existing and future video standards. The existing MPEG-4 part 2 standard, now almost 20 years old, provides the ability to store objects in separate layers, and includes a sprite mode where the background layer is generated by cropping a still image based on frame-wide global motion parameters, but videos containing more general background motion cannot be effectively encoded with sprite mode. We have developed a perceptually motivated lossy compression algorithm, where oscillatory background motion can be compactly encoded. Our model achieves a low bit rate by referencing a time-invariant representation of the optical flow with only a few added parameters per frame. At very low bit rates, our technique can provide dynamic backgrounds at a visual quality that may not be achievable by traditional methods which are known to produce unacceptable blocking and ringing artifacts. In the figure below, (left) Sample still frames taken from decompressed video as encoded in camera (click to see full size); (middle) complex valued mode of horizontal motions; (right) vertical motions, taken from a still frame of filtered motions in the time domain. To represent complex numbers using color, complex valued images are decoded as though they were in HSV format, with phase mapped to hue and amplitude mapped to value.
Here is a depiction of our video encoding pipeline. On the left modal parameters are estimated from a short video clip, and on the right; motion vectors are filtered and projected onto the modal basis to generate global motion parameters.
The figure below compares snapshots from video clips.
Figure 5: Left column: Sample frames from the original MP4 videos as encoded by the camera. Middle Left column: Expanded view of the box portion shown in the left column taken from AVC encodings. Middle Right Column: Expanded view of the box portion shown in the left column taken from HEVC encodings. Right column: Expanded view of the box portion shown in the left column taken from our decoded videos. Numbers below each frame represent file size (left) and PSNR compared with the original video as compressed in camera (right).PSNR numbers are an average over the video frames of the luminance channel as computed by ffmpeg.
Here is a reference to a paper presents this work:
- A. Prakash, N. Moran, S. Garber, A. DiLillo, and J. A Storer [2019]. "Compact Representations of Dynamic Video Background Using Motion Sprites", IEEE Data Compression Conference (DCC) 2019.
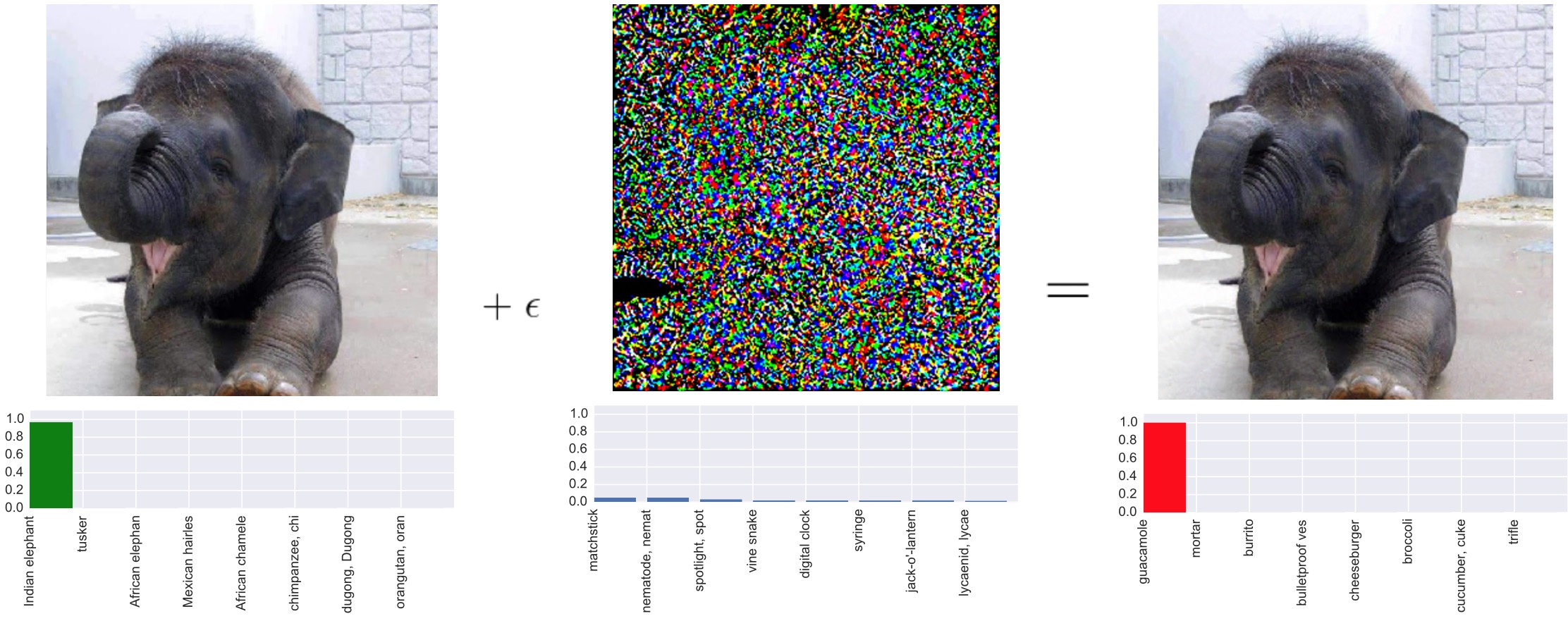
As deep neural networks (DNNs) have been integrated into many commercial systems, methods have been developed to attack images that are subjects of classification or object recognition by such systems. An attacker can carefully manipulate pixel values with imperceptible perturbations to cause a model to misclassify images. In fact, the misclassification can be targeted to cause a modelN to miss-classify an image to a particular chosen class. The figure below shows on the left the original image, in the center adversarial noise, and on the right an image produced by the adversary that looks to the eye the same as the original but gets misclassified by a state-of-the-art classifier. The left image is classified as elephant, whereas the right image is classified as guacamole.
We present an algorithm to process an image so that classification accuracy is significantly preserved in the presence of such adversarial manipulations. Image classifiers tend to be robust to natural noise, and adversarial attacks tend to be insensitive to object location. We leverage model robustness to defend against adversarial perturbations by forcing the image to match natural image statistics. With only a modest increase in encoding time our method produces images with high visual quality while greatly reducing the potency of state-of-the-art attacks. For the case of jpeg compressed images, a version of our method produces a new protected JPEG image that can be decoded by any off-the-shelf JPEG decoder.
For further information and references see:
- A. Prakash, N. Moran, S. Garber, A. DiLillo, and J. A Storer [2018]. "Deflecting Adversarial Attacks with Pixel Deflection", CVPR.
- A. Prakash, N. Moran, S. Garber, A. DiLillo, and J. A Storer [2018]. "Protecting JPEG Images Against Adversarial Attacks", IEEE Data Compression Conference, 139-148.
It has long been considered a significant problem to improve the visual quality of lossy image and video compression. Recent advances in computing power together with the availability of large training data sets has increased interest in the application of deep learning CNNs to address image recognition and image processing tasks. We have employed a powerful CNN tailored to the specific task of semantic image understanding to achieve higher visual quality in lossy compression. A modest increase in encoding complexity allows a standard off-the-shelf JPEG decoder to be used for decoding. While JPEG encoding may be optimized for generic images, the process is ultimately unaware of the specific content of the image to be compressed. Our technique makes JPEG content-aware by designing and training a model to identify multiple semantic regions in a given image. With the same compression ratio and same PSNR, our algorithm can provide better quality in areas of interest in an image. For example, the figure below compares close-up views of a salient object in a standard JPEG and our new content-aware method:

Unlike object detection techniques, our model does not require labeling of object positions and is able to identify objects in a single pass. Our a new CNN architecture directed specifically to image compression, generates a map that highlights semantically-salient regions so that they can be encoded at higher quality as compared to background regions. For example, the figure below shows a comparison of our model (MS-ROI) with CAM and human fixation; our model identifies the face of the boy on the right, as well the hands of both children:

By adding a complete set of features for every class, and then taking a threshold over the sum of all feature activations, we generate a map that highlights semantically-salient regions so that they can be encoded at a better quality compared to background regions. In experiments with the Kodak PhotoCD dataset and the MIT Saliency Benchmark dataset, our algorithm achieves higher visual quality for the same compressed size (and same PSNR). For example, the figure below shows a sample of five of these images, along with the corresponding heat maps generated by our algorithm; the first four show typical results which strongly capture the salient content of the images, while the fifth is a rare case of partial failure, in which the heat map does not fully capture all salient regions.

Our variable compression improves upon visual quality without sacrificing compression ratio. Encoding requires a single inference over the pre-trained model, the cost of which is reasonable when performed using a GPU card, along with a standard JPEG encoder. The cost of decoding, which employs a standard, off-the-shelf JPEG decoder remains unchanged. We believe it will be possible to incorporate our approach into other lossy compression methods such as jpeg 2000 and vector quantization, a subject of future work.
For further information and references see:
- A. Prakash, N. Moran, S. Garber, A. DiLillo, and J. A Storer [2017]. "Semantic Perceptual Image Compression using Deep Convolution Networks", IEEE Data Compression Conference, 250-259.
- A. Prakash and J. A. Storer [2016]. "Highway Networks for Visual Question Answering", VQA Workshop, CVPR 2016.
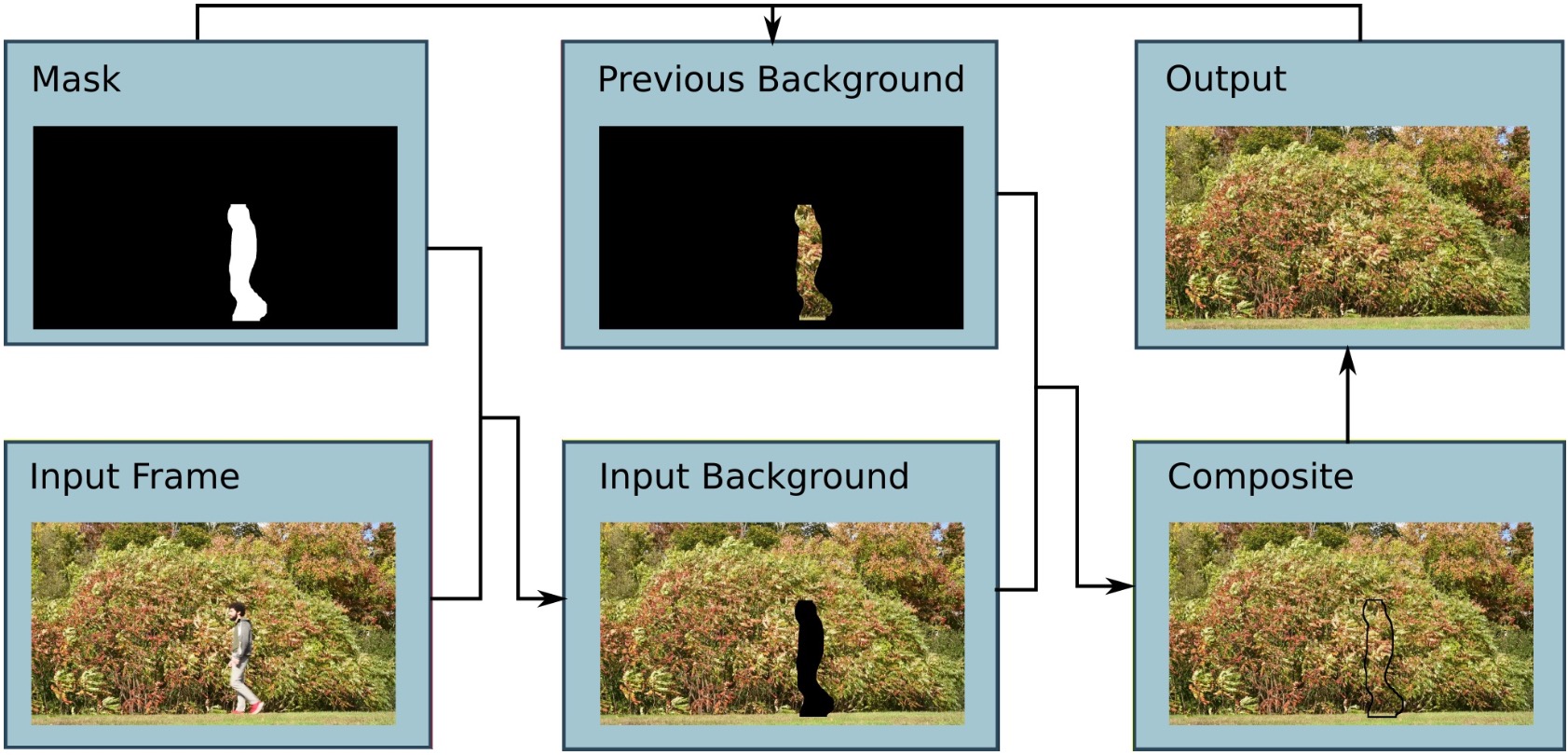
We are interested in automatic techniques for creating a video summary of a chalkboard lecture with the speaker removed, and for generating a set of slides containing all of what was written but without the lecturer present. Our system works by continuously subtracting the speaker from the video feed using a region based correlation feature. From this new version of the video that no longer contains the speaker the final presentation slides are extracted.
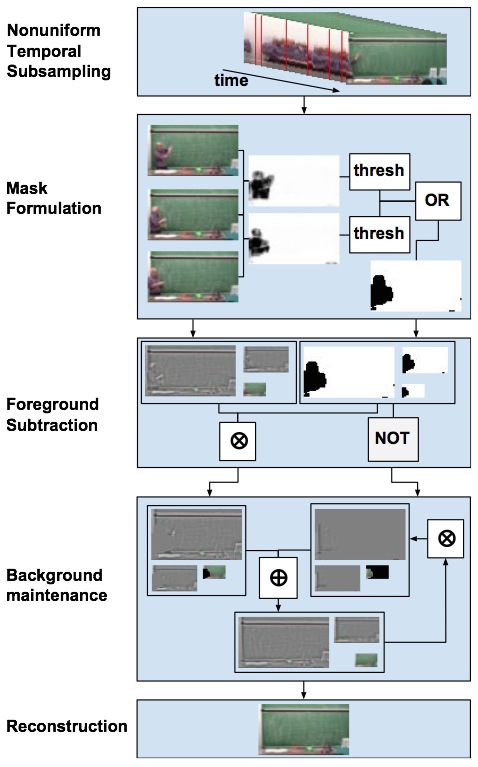
As shown in the figure on the left below, in the sampling stage, we take a nonuniform sampling from the input feed based on absolute frame difference. Next, in the foreground subtraction stage, we calculate the localized correlation coefficient computed over a sliding window, and apply a threshold to the results to obtain a foreground mask. Once the mask is obtained we use it to update coefficients of a background image pyramid. This pyramid is then reconstructed and added to the output stream. The bottom level of this pyramid, containing high frequency edge components over the whole frame, is weighted using a Gaussian window and then the L1 norm is taken over the weighted frame for further processing in the key frame detection stage.
 |
 |
We have tested our system on blackboard and whiteboard videos gathered from YouTube. The output of the foreground subtraction stage reliably contained all content written on the board during the lecture with minimal ghost artifacts. The final slideshows generated by the peak-finding stage contained the desired slides. For example, the figure on the right above shows at the top one of the original frames of a 50 minute video of a professor lecturing on a blackboard, and below that 7 summary slides constructed by our system which contain all of the content written on the blackboard with the lecturer removed. Note the cloudy areas of the board in slides 5 and 6 are due to natural sunlight that came in during the lecture, and are not an artifact of our process. In addition to these 7 slides the system also produced three redundant slides. Although it is easy to flip through the final slides and discard the redundant ones, we are currently working on an automatic method.
For further information and references see:
- S. Garber, L. Milekic, A. Prakash, N. Moran, A. Di Lillo, and J. A. Storer [2017]. "A Two Tier Approach To Blackboard Video Lecture Summary", IMVIP - Irish Machine Vision and Image Processing Conference, Maynooth University, Ireland, pages 68-75; see http://eprints.maynoothuniversity.ie/8841/1/IMVIP2017_Proceedings.pdf.
- S. Garber, L. Milekic, A. Prakash, N. Moran, A. DiLillo, and J. A. Storer [2017]. "Visual Lecture Summary Using Intensity Correlation Coefficient", FIE - Frontiers in Education Conference, Indianapolis, IN.
We have addressed the problem of retrieving the silhouettes of objects from a database of shapes with a translation and rotation invariant feature extractor successfully used by the same authors to classify textures. We retrieve silhouettes by using a "soft" classification based on the Euclidean distance. Experiments show significant gains in retrieval accuracy over previous work when applied to the MPEG7 CE-Shape 1 database. An interesting aspect of this approach is the use of a unique descriptor for both texture and shape recognition.

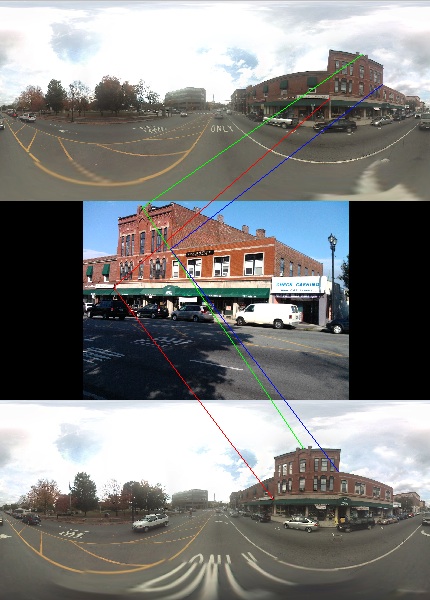
We are interested to applying object recognition algorithms to location and assistance algorithms. We have developed tools that can be used within a larger system referred to as a passive assistant. The system receives information from a mobile device, as well as information from an image database such as Google Street View, and employs image processing to provide useful information about a local urban environment to a user who is visually impaired. The first stage acquires and computes accurate location information, the second stage performs texture and color analysis of a scene, and the third stage provides specific object recognition and navigation information. These second and third stages rely on compression-based tools (dimensionality reduction, vector quantization, and coding) that are enhanced by knowledge of (approximate) location of objects. In a preprocessing phase (that is done only once at image acquisition time) a set of key points with associate feature vectors is calculated for each relevant database image, and then a small set of corresponding points in two overlapping database images (e.g., successive images in Google Street View) are identified. The intersection of the two lines of sight from the acquisition coordinates to a pair of corresponding key points provides their coordinates. Appropriate ranking and weighted averaging of matching pairs can be used to refine accuracy and confidence. The preprocessing step creates geo-located key points along with their associated feature vectors. When a user image has at least three points that can be matched with these database key points, a resection procedure like that used in land surveying can be employed: that is, from the apparent angles between these three points, as seen by the user, and the (already computed) locations of the points, we compute the location of the user. In the figure below, the top and bottom images are two images from the Google Street View database, and the middle image is the user image. Feedback between this computation and revised estimates of position based on object recognition allows for a precise location of the user that can be the basis for user assistance (e.g., at doorways and intersections).
For further information and references see:
-
A. DiLillo, A. Daptardar, G. Motta, K. Thomas, and J. A. Storer [2012].
"Compression-Based Tools for Navigation with and Image Database",
Algorithms 5, 1-17.
- A. DiLillo, A. Daptardar, G. Motta, K. Thomas, and J. A. Storer [2012]. "Applications of Compression to Content Based Image Retrieval and Object Recognition", Proceedings International Conference On Data Compression, Communication, and Processing (CPP 2011), Palinuro, Italy, 179 - 189.
- A. DiLillo, G. Motta, and J. A. Storer [2010]. "A Rotation And Scale Invariant Descriptor For Shape Recognition", Proceedings International Conference On Image Processing (ICIP), Hong Kong, MA-L9:1, 257-260.
- A. DiLillo, G. Motta, K. Thomas, and J. A. Storer [2010]. "Shape Recognition, With Applications To A Passive Assistant", Proceedings PETRA - PErvasive Technologies Related to Assistive Environments, Samos, Greece, June 23-25; also in ACM International Conference Proceedings Series.
- A. Di Lillo, G. Motta, and J. A. Storer [2010]. "Shape Recognition Using Vector Quantization", Proceedings Data Compression Conference, IEEE Computer Society Press, 484-493.
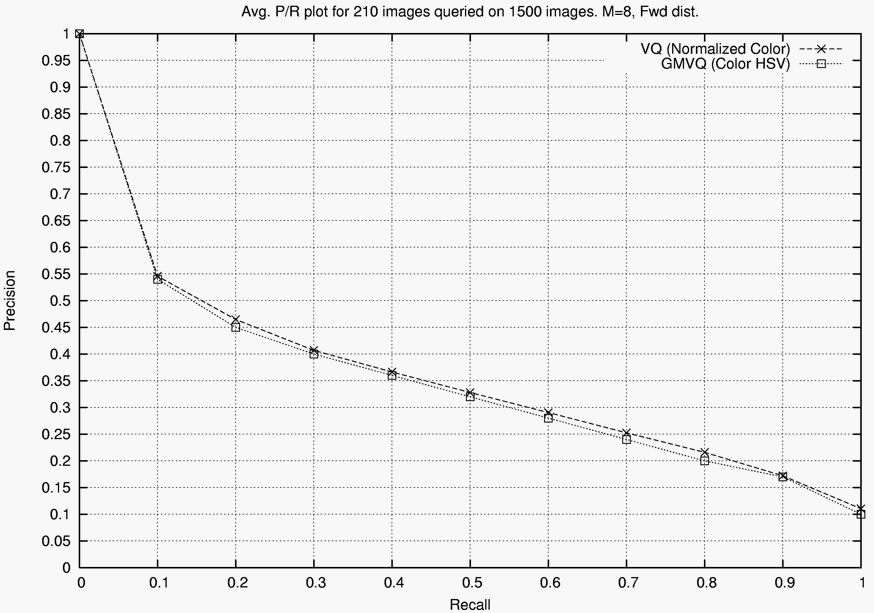
We have investigated a low complexity approach for content-based image retrieval (CBIR) using vector quantization (VQ). The hope is that encoding an image with a codebook of a similar image will yield a better representation than when a codebook of a dissimilar image is used. Our most simple method tags each image with a thumbnail and a small VQ codebook of only 8 entries, where each entry is a 6 element color feature vector. If we think of a web crawler where the image database is being dynamically updated, the preprocessing can be thought of as a tagging of images as they are gathered. We use a simple mean squared error computation for the distance function for retrieval. To test our method, we have used for our database a subset of the COREL collection consisting of 1,500 JPEG images, 100 in each of 15 classes; three typical images from each class are shown below. These images are already relatively small, but still larger than is needed for a thumbnail. To create the database thumbnails, the system retains the central region (256 x 256 for these images) and scales it to 128 x 128 for each image (although it is possible to use smaller thumbnails, this size has allowed us to make direct comparisons with previous work).

The graph shown below compares the precision-recall tradeoff of our simple VQ algorithm to that of a more complex method based on GMVQ from the previous literature. Using the same code, with the appropriate places modified (distance function, etc.), VQ retrieval used on the average 1/3 of the time of GMVQ (that is the total time to perform a retrieval of each of the 1,500 images on the entire 1,500 image set was more than three times greater for GMVQ than VQ), while achieving the same or slightly better performance.
We have also considered extending our basic VQ approach presented in the previous section by adding positional information to each feature vector. That is, the mean XY coordinates of all blocks associated with a particular codebook entry are added to that entry (so the dimension of codebook entries is increased from 6 to 8). The figure below shows some database images with the code vector positions marked on the image. The color within each black bordered box represents the color of the code vector.

In general, the addition of XY coordinate features gives an overall modest improvement in retrieval quality. However, the real benefit of adding XY to the feature vector comes as "insurance" on classes with highly contrasting regions. For example, the first figure below shows the first 10 images retrieved for one of the dinosaur images with color only and the second figure below shows the first 10 for color + XY.
Without XY features:

With XY features:

We have performed some additional experiments to incorporate positional information implicitly. The system computes similarity between corresponding image regions, where separate VQ codebooks trained on color feature vectors are associated with each region. To compare a query image with a database image, the total similarity score is the sum of the scores for each region, where the score for a region is the MSE when the query image features for that region are encoded using a database image's VQ codebook for that region. The size of each region codebook is varied by query and region by setting the query threshold. This parameter will determine how many codewords to use when encoding a query. Since the database codebook size needs to be varied based on the query image statistics, we use tree-structured codebooks (TSVQ) for the database images. After partitioning the image into regions, we train relatively large TSVQ codebooks by successively splitting nodes with the largest distortion until we arrive at the desired number of leaf codewords. That is, before codebooks of a given database image are used to encode the regions of the query image (to test similarity with that database image), each codebook is pruned to the same size as the codebook for that region associated with the query image. The figure below shows two images from the database and the number of codebook entries for each region using a threshold of 1,500.
 |
 |
For further information and references see:
-
A. H. Daptardar and J. A. Storer [2008].
"VQ Based Image Retrieval Using Color and Position Features",
Proceedings Data Compression Conference,
IEEE Computer Society Press,
432-441.
-
A. H. Daptardar and J. A. Storer [2006].
"Reduced Complexity Content-Based Image Retrieval using Vector Quantization",
Proceedings Data Compression Conference,
IEEE Computer Society Press, 342-351.
- A. H. Daptardar and J. A. Storer [2005]. "Content-Based Image Retrieval Via Vector Quantization", In Advances in Visual Computing - Springer Lecture Notes in Computer Science 3804/2005 (ISBN 3-540-30750-8), 502-509; also appeared in International Symposium on Visual Computing, December 5-7, 2005.
Click here for 2008 Dcc paper experiments.
We have developed a prototype texture analysis algorithm that achieves state of the art performance. While there is no agreement on a formal definition of texture, it is commonly accepted that textures are naturally extracted and recognized as such by the human visual system. Furthermore, human experiments have shown that the visual cortex contains orientation and scale band-pass filters for vision analysis. The vast majority of the methods proposed in the literature are translation invariant, but assume that textures are presented or acquired at the same orientation and scale. For many types of image acquisition, this assumption is unrealistic. Scale is often determined by metadata (e.g., camera settings recorded in a standard JPEG / EXIF file), but there can be little control over information about rotation. Rotation invariance can be key to practical texture analysis. Furthermore, human experiments have shown that images subject to rotation (and other affine transforms such as scaling and translation) are still perceived as the same image. It is also widely believed that the visual system extracts relevant features in the frequency domain, independently of their orientation. The basic steps of our feature extractor are shown in the figure below. The features for an image pixel are collected from a square window around the pixel. This window is weighed by a 2-dimensional Hamming window before applying a bi-dimensional Fourier transform, after which the magnitude of the coefficients is further transformed into polar coordinates. Taking the magnitude of the Fourier coefficients provides translational invariance. The representation in the polar coordinates of the Fourier coefficients provides already an excellent characterization of the textural features. Preliminary results on the supervised segmentation of a standard database show that this method matches the performance of the state-of-the-art. Rotating the input image by an angle also rotates the transformed Fourier coefficient by the same angle, so when the magnitude of the Fourier transform is mapped to polar coordinates, a rotation becomes a translation along the angle axis. The application of a second Fourier transform along the angle axis is sufficient to extract a set of features that are rotationally invariant.

Capturing textural features requires a large window and results in feature vectors having many components. If a multi-scale method is being used, the number of components will grow linearly with the number of resolutions used. Besides the obvious issues of time and space complexity, the components of these vectors are often highly correlated and/or not useful to discriminate among textures. To reduce the dimension of the feature vectors we have employed Principal Component Analysis (PCA). PCA performs an orthonormal transformation on the feature space that retains only significant eigenvectors of the whole dataset, called principal components. The feature space is transformed and information is compacted into the smallest number of dimensions by discarding redundant features. PCA reduces the number of dimensions without considering their usefulness to the classification. Feature vectors so constructed are classified using vector quantization. A simple post-processing filter inspired by the Kuwahara filter divides a square neighborhood of each pixel into four overlapping quadrants, each containing the central pixel. The histogram of the indices and the entropy of the values is computed in each quadrant, and replaces the central index with the highest-frequency index belonging to the quadrant with the smallest entropy. We have compared the performance of our texture analysis algorithm for both classification and image segmentation problems to the work of others. For classification on texture databases used by others, we have achieved 99% overall accuracy, including rotations of 5, 10, 15, 30, 45, 60, 75, and 90 degrees. We have also performed experiments on compositions of texture images from these databases. For example, consider the two texture problems shown below. The one on the left is composed of the first 8 images of the Outex_TC_00010 set of 24 textures (arranged in row major order) and the one on the right is composed of every third image of this set (arranged in row major order). Rather than trying to rotate these two problems at different angles, we made 6 different classifiers, each trained on the 8 textures rotated at a particular angle (5, 10, 15, 30, 45, 60, 75, and 90 degrees), and then applied these 6 classifiers to the non-rotated problems. The performance for each of these angles (percentage of pixels correctly classified) given in the table below the figure; these figures represent a significant improvement over the state of the art represented by the work of previous authors mentioned above.
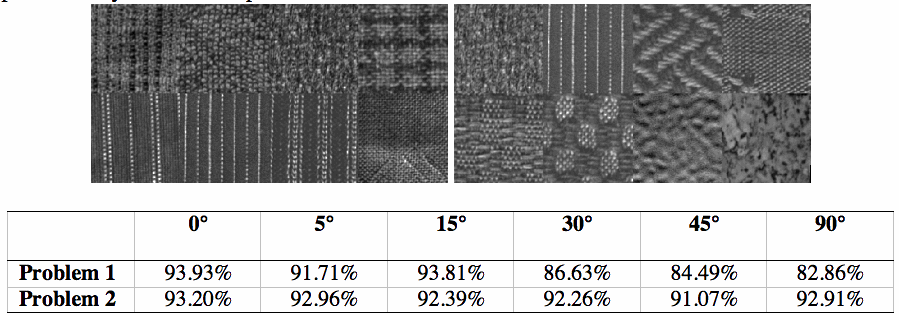
For another example, the figure below shows on the left one of the more complex image problems from the database, in the middle the perfect partitioning (random colors are used) and on the right the partitioning achieved by our algorithm at 0 degrees of rotation. Here the percentage of correctly classified pixels is 82%, less than what is typical in the example above, but quite reasonable considering the extent of boundary areas in this problem.

For further information and references see:
-
A. DiLillo, G. Motta, and J. A. Storer [2008].
"Multiresolution Rotation-Invariant Texture Classification
Using Feature Extraction in the Frequency Domain and Vector Quantization",
Proceedings Data Compression Conference,
IEEE Computer Society Press,
452-461.
-
A. DiLillo, G. Motta, and J. A. Storer [2007].
"Texture Classification Based on Discriminative Feature Extracted in the Frequency Domain",
Proceedings IEEE International Conference on Image Processing (ICIP),
II.53-II.56.
-
A. DiLillo, G. Motta, and J. A. Storer [2007].
"Supervised Segmentation Based on Texture Signature Extracted in the Frequency Domain",
Third Iberian Conference on Pattern Recognition and Image Analysis (IbPRIA).
- A. DiLillo, G. Motta, and J. A> Storer [2007]. "Texture Classification Using VQ with Feature Extraction Based on Transforms Motivated by the Human Visual System", Proceedings Data Compression Conference, IEEE Computer Society Press, 392.
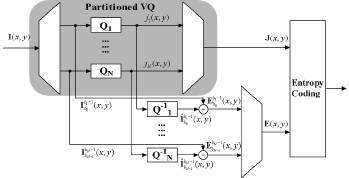
Remote sensing technology has shifted from panchromatic data (a wide range of wavelengths merged into a single response), through multispectral (a few possibly overlapping bands in the visible and infrared range with spectral width of 100 200nm each), to hyperspectral imagers and ultraspectral sounders, with hundreds or thousands of bands. In addition, the availability of airborne and spaceborne sensors has increased considerably, followed by the widespread availability of remote sensed data in different research environments, including defense, academic, and commercial. In hyperspectral photography, each pixel records the spectrum (intensity at different wavelengths) of the light reflected by a specified area, with the spectrum decomposed into many adjacent narrow bands. Data compression plays a key role in the original transmission of imagery to a central location, in the archiving of data sets, and in the distribution of data to users.
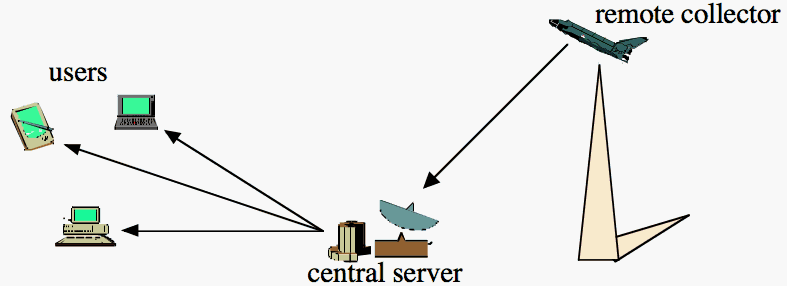
We have considered a number of approaches to hyperspectral image compression, including the ones where vector quantization is applied independently to each pixel in a way that preserves uniform quality across all vector components. That is, high dimensional source vectors are partitioned into a number of subvectors of (possibly) different length and then each subvector is individually encoded with an appropriate codebook and distortion measure. Then an entropy coder that may exploit spatial correlations is employed for both the VQ indices and residual. This scheme allows efficient lossless, near lossless, or lossy compression of high dimensional data sources such as hyperspectral imagery in which each vector component is allowed to have different alphabet and distribution. A key advantage of our approach is the use of independent small VQ codebooks that allow fast encoding and decoding. Motivated by the need of maintaining uniform quality across all vector components, especially for applications needing target identification, our experiments have used the Percentage Maximum Absolute Error (PMAE) as the distortion measure.
For further information and references see:
-
G. Motta, F. Rizzo, and J. A. Storer [2006], editors.
Hyperspectral Data Compression,
Springer
(hard cover, 425 pages).
- F. Rizzo, G. Motta, and J. A. Storer [2005]. "Compression of Hyper/Ultra-Spectral Data", Proceedings of SPIE, Optics and Photonics, Satellite Data Compression, Communication and Archiving, Vol. 5889, pp. 588908-1--588908-10.
-
F. Rizzo, B. Carpentieri, G. Motta, and J. A. Storer [2005].
"Low Complexity Lossless Compression of Hyperspectral Imagery via Linear Prediction",
IEEE Signal Processing Letters 12:2, 138-141.
-
F. Rizzo, B. Carpentieri, G. Motta, and J. A. Storer [2004].
"Compression of Hyperspectral Imagery",
Proceedings International Conference on E-Business and Telecommunications (ICETE),
Sebutal, Portugal, 2004;
an extended version is a chapter in the book E-Business and Telecommunication Networks,
Edited by J. Ascenso, L. Vasiu, C. Belo, and M. Saramago, Kluwer / Springer (2005).
-
F. Rizzo, B. Carpentieri, G. Motta, and J. A. Storer [2004].
"Real-Time Software Compression and Classification of Hyperspectral Images",
11th SPIE International Symposium on Remote Sensing Europe,
Maspalomas,
Gran Canaria,
Spain, Sept. 13-17, 5573-17.
-
F. Rizzo, B. Carpentieri, G. Motta, and J. A. Storer [2004].
"Lossless Compression of Hyperspectral Imagery: A Real Time Approach",
11th SPIE International Symposium on Remote Sensing Europe,
Maspalomas,
Gran Canaria,
Spain,
Sept. 13-17, 2004, 5573-25.
-
G. Motta, F. Rizzo, J. A. Storer, and B. Carpentieri [2004].
"High Performance Compression of Hyperspectral Imagery
with Reduced Search Complexity in the Compressed Domain",
Proceedings Data Compression Conference, IEEE Computer Society Press,
479-488.
-
G. Motta, F. Rizzo, and J. A. Storer [2003].
"Partitioned Vector Quantization: Application to Lossless
Compression of Hyperspectral Images",
Proceedings International Conference on Acoustics, Speech, and Signal Processing (ICASSP);
presented at
IEEE International Conference on Multimedia and Expo (ICME2003).
- G. Motta, F. Rizzo, and J. A. Storer [2003]. "Compression of Hyperspectral Imagery", Proceedings Data Compression Conference, IEEE Computer Society Press, 333-342.
Identifying similar strings is a problem that arises in many applications. Internet search algorithms and database retrieval algorithms, including tasks in bioinformatics, can employ effective string similarity testing to process queries. The completion of the human genome as well as that for other species has produced large strings in which researchers are looking for structure. Differencing algorithms used by software updates and backup systems can be improved with string similarity algorithms. The traditional edit-distance problem is to find the minimum number of insert-character and delete-character (and sometimes change character) operations required to transform a string S (the source string) to become a string T (the target string); that is, starting with S, repeatedly perform operations until we have T, and do so using a minimum number of operations. However, there are many other natural operations that can be used to transform S to become T, including copies, moves, deletes, and reversals of blocks of characters. However the problem complexity is greater (NP-hard in many cases) and efficient approximation algorithms are needed. If the copy operation is allowed, then efficient approximation algorithms that employ data compression techniques can be employed, with applications to differential file compression. In fact, in many practical applications, differential file compression can be performed in-place with performance comparable to the best methods that work with unrestricted memory. In-place differential file compression has the advantage that the sender need not make any assumptions about the resources available to the receiver, or in the case of file back-up systems that work in the background, fewer resources must be claimed. That is, even if other operations are allowed as well, the copy operation is sufficiently powerful, that it alone can achieve efficient approximation. We have considered just the move operation (or the move operation in combination with the insert-character and delete-character operations), just delete operations (possibly with insert-character operations - which is not NP-hard), or combinations of move and delete operations (and possibly insert-character operations). One way to model the move operation is to view strings as linked lists (one character per vertex) and allow the insert and delete operations to be applied to both vertices and links. Although one would not likely represent strings this way in practice, it points out a fundamental difference between these operations and the copy operation; that is, move and delete operations can be done in O(1) time on linked lists whereas copy operations cannot. For many applications, the rearrangement implied by move operations (possibly together with delete and insert-character operations) may better reflect string similarity than the ability to compress the string with respect to another, as is in some sense implied by the copy operation. Because optimal differential compression and generalized edit distance is in general NP-hard, in past work we have studied approximation algorithms and their efficient implementation. Shapira and Storer [2002] consider approximation algorithms for generalized edit distance where block-moves are allowed. Shapira and Storer [2003] present the IPSW algorithm for in-place differential file compression (no more than MAX(m,n) + O(1) space is used where m is the size of S and n is the size of T). IPSW uses a sliding window method to decompress T by initializing the window to S, and restricting its maximum size to max(|S|,|T|); except for the beginning, copies cannot reach all the way back to the start of S, and while decoding in-place, the no longer accessible portion of S is overwritten from left to right.

IPSW is fast and the compression achieved compares well with other existing methods, including those that are not in-place. IPSW is most effective when there is a reasonable degree of alignment between S and T. That is, large matches between S and T occur in approximately the same relative order. Such alignment is typical for many applications, such as subsequent backups of the same data, where when new data is inserted, and other data is deleted, the remaining data often comprises aligned common substrings. We have also considered methods with good performance in-place even for those (rare) cases where S and T are not sufficiently well aligned. This could happen, for example, when for some reason large blocks of the file have been moved around to form a new version of the file. An extreme case is when the first and second halves of S have been exchanged to form T (S = uv and T = vu); to decompress T the IPSW algorithm overwrites u as it copies v, and then the ability to represent v with a single copy is lost. Rather than modify IPSW, a very fast and practical method that suffices for many and perhaps most practical inputs, is a preprocessing stage for IPSW that moves substrings within S to better align S with T. Compressed files can be preceded with an initial bit indicating whether preprocessing has occurred. The encoder can compress T with IPSW and compare that to compressing T with respect to S not in place (so at all times all substrings of S are available to be copied). If the difference is significant, this initial bit can be set, alignment preprocessing performed, and a list of moves prepended the normal IPSW encoding. The decoder can perform the moves (in-place) and then proceed in-place with normal IPSW decoding. For move pre-processing, we distinguish employ two different kinds of rearrangements of the blocks. Moves rearrange the blocks so that they occur in S and T at the same order. "Jigglings" move the junk blocks of S backwards in the file, so that, as a side affect, the matched blocks are moved forwards. Move Preprocessing Algorithm:
Step 1: Find Non Overlapping Common Substrings (NOCS) from longest to shortest down to length of a constant K.Under reasonable assumptions, all of the preprocessing steps 1 through 4 can be done in linear time.
Step 2: Compute the minimum number of rearrangements (moves and jigglings) in S so that the blocks are left copies within S and T.
Step 3: Generate S' according to step 2.
Step 4: Compute IPSW(S',T).
For further information and references see:
- D. Shapira and J. A. Storer [2011]. "Edit Distance With Block Deletions", Algorithms 4, 40-60.
-
D. Shapira and J. A. Storer [2007].
Edit Distance with Move Operations",
Journal of Discrete Algorithms 5:2,
380-392.
-
D. Shapira and J. A. Storer [2005].
"In-Place Differential File Compression",
Computer Journal 48:6,
677-691.
-
D. Shapira and J. A. Storer [2004].
"In-Place Differential File Compression of Non-Aligned Files
With Applications to File Distribution and Backups",
Proceedings Data Compression Conference (DCC),
IEEE Computer Society Press, 82-91.
-
D. Shapira and J. A. Storer [2003].
"In-Place Differential File Compression",
Proceedings Data Compression Conference (DCC),
IEEE Computer Society Press,
263-272.
-
M. Meyerovich, D. Shapira, and J. A. Storer [2003].
"Finding Non-Overlapping Common Substrings in Linear Time",
Proceedings Symposium on String Processing and Information Retrieval (SPIRE),
369-377.
- D. Shapira and J. A. Storer [2002]. "Generalized Edit Distance with Move Operations", Thirteenth Annual Symposium on Combinatorial Pattern Matching (CPM), 85-98.
- F. Mignosi, A. Restivo, M. Sciortino, and J. A. Storer [2000]. "On Sequence Assembly", Technical Report, Computer Science Department, Brandeis University.
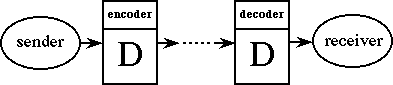
There has been much past work concerning the detection and correction of errors on a communication line. However, with on-line data compression where a sender and receiver are in lock-step maintaining constantly changing identical local memories, a single error on the communication channel or storage medium could cause the dictionaries of the encoder and decoder to differ, which in the worst case could corrupt all data to follow. That is, since decoding is only guaranteed to be correct when the dictionary remains the same as the one used to encode the data, there is no way to bound the effects of a single error in the worst case (and, in fact, the expected case is very bad because a single error can corrupt the mapping between codewords and dictionary entries). With data storage devices or one-way communication channels, where the decoder cannot send messages to the encoder, the problem becomes even more critical. In addition, with many existing communication systems where the full bandwidth of the channel is consumed, even if a two-way channel is available to let the encoder know that an error has occurred, re-transmission of data can often be tantamount to losing new data that could have been transmitted during the time used to re-transmit the old data. Re-transmission can also introduce further error propagation problems. Even if error detection and correction methods are available that make the probability of an error getting through sufficiently low, error propagation prevention may be all that is needed for non-critical applications such as web browsing, email processing, etc. We have developed the k-error protocol, a technique for protecting a dynamic dictionary method from error propagation as the result of any k errors on the communication channel or compressed file. In addition theoretical results show that at no asymptotic loss of compression, high probability protection against error propagation resulting from a sustained error rate is also a benefit of the protocol. Experiments show that this approach is highly effective in practice with a low overhead. For LZ2-based methods that "blow up" as a result of a single error, with the protocol in place, high error rates can be sustained without error propagation (the only corrupted bytes decoded are those that are part of the string represented by a pointer that was corrupted).
For further information and references see:
-
J. A. Storer [2000].
"Error Resilient Dictionary Based Compression",
Proceedings of the IEEE 88:11,
1713-1721.
-
J. A. Storer and J. H. Reif [1997].
"Low-Cost Prevention of Error-Propagation for Data Compression
with Dynamic Dictionaries",
Proceedings1997 IEEE Data Compression Conference,
171-180.
- J. A. Storer and J. H. Reif [1997]. "Error Resilient Optimal Data Compression", SIAM Journal of Computing 26:3, 934-939.
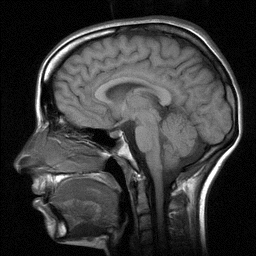
We are studying adaptive vector quantization where the codebook is learned as the image is processed in a single pass (i.e., the codebook contains a changing set of variable-size vectors). Experiments with a variety of data types (gray scale and color magazine photos, medical images, space images, finger prints, handwriting, etc.) show that with no prior knowledge of the data and no training, for a given fidelity this approach compares favorably with traditional VQ that employs codebooks that have been trained on the type of data being compressed (it typically at least equals and often greatly exceeds the amount of compression achieved by the JPEG standard). We have developed efficient parallel algorithms and architectures as well as fast sequential implementations using KD-trees. Key advantages of this approach are that it is adaptive (no advance knowledge of the data or training is required), the tradeoff between the fidelity and the amount of compression can be continuously varied (and automatically controlled), precise guarantees on the amount of distortion on any small area of the image (e.g., 4x4 array of pixels) can be provided, and decoding is extremely fast because it involves primarily table lookup like traditional VQ (encoding is on the same order of complexity as for traditional VQ). The figure below shows an image of a brain on the left and a "map" of the decompressed image on the right (each rectangle has been colored with a random solid color).
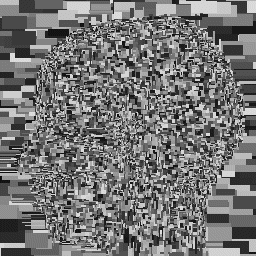
For further information and references see:
-
F. Rizzo, J. A. Storer, and B. Carpentieri [2001].
"LZ-Based Image Compression",
Information Sciences 135,,
107-122.
-
F. Rizzo and J. A. Storer [2001].
"Overlap in Adaptive Vector Quantization",
Proceedings Data Compression Conference,
IEEE Computer Society Press,
401-410.
-
G. Motta, F. Rizzo, and J. A. Storer [2000].
"Image Compression",
Encyclopedia of Computer Science,
Nature Publishing Group, London, 836-840.
-
F. Rizzo, J. A. Storer, and B. Carpentieri [1999].
"Improving Single-Pass Adaptive VQ",
IEEE International Conference on Acoustics, Speech, and Signal Processing,
IMDSP2.10;
also see the article by the same authors:
"Experiments with Single-Pass Adaptive Vector Quantization",
Proceedings IEEE Data Compression Conference,
546.
-
C. Constantinescu and J. A. Storer [1994].
"On-Line Adaptive Vector Quantization with Variable Size Codebook Entries",
Information Processing and Management 30:6,
745-758.
-
C. Constantinescu and J. A. Storer [1994b].
"Improved Techniques for Single-Pass Vector Quantization",
Proceedings IEEE (June),
933-939.
-
J. Lin and J. A. Storer [1994].
"Design and Performance of Tree-Structured Vector Quantizers",
Information
Processing and Management 30:6,
851-862.
Lin).
-
M. Cohn, E. Lin, and J. A. Storer [1992].
"Optimal Pruning for Tree-Structured Vector Quantization",
Information Processing and Management 28:6,
723-733.
-
J. Lin and J. A. Storer [1992].
"Improving Search for Tree-Structured Vector Quantization",
Proceedings IEEE Data Compression Conference,
339-348.
-
J. Lin and J. A. Storer [1991].
"Resolution Constrained Tree Structured Vector Quantization for Image Compression",
Proceedings IEEE Symposium on Information Theory,
Budapest, Hungary.
- J. A. Storer [1990]. "Lossy On-Line Dynamic Data Compression", Combinatorics, Compression, Security and Transmission, Springer-Verlag, 348-357.
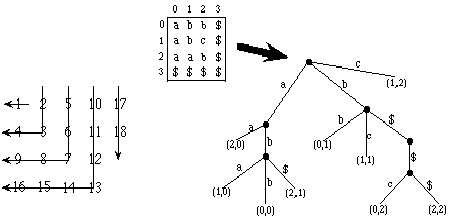
Lossless image compression, particularly bi-level image compression (where pixels are 0 or 1) has often employed techniques quite separate from those used for text compression or lossy image compression; most standards today employ modeling followed by coding (e.g., the JBIG standard, the IBM Q-coder, CCITT Group 4). Constantinescu and Storer [1994] present a lossy image compression scheme that can be viewed as a generalization of lossless dynamic dictionary compression ("LZ2" type methods) to two dimensions with approximate matching; Constantinescu and Storer [1995] have experimented with this approach for lossless image compression with great success. In this research we have generalized "LZ1" type methods (that employ displacement/length pointers to the previously seen text) to lossless image bi-level compression. We make use of a generalization of the suffix trie data structure for two dimensions that was introduced by Giancarlo [1995]. In a two dimensional suffix trie, the suffix at a position (i,j) in the two dimensional input array is just the portion of the array going to the right and down from that position. We list the characters of a suffix in the order depicted on the left in the figure below. Similar to the standard convention used in the one dimensional case, we pad the right and bottom sides of the array with a special character $ as a notation convenience. On the right in the figure below is an example of a 3x3 array (padded to a 4x4 array with $'s) and its corresponding 2D suffix trie. We have generalized the LZ1 approach to two dimensions and confirmed that, like the 1-dimensional case, the complexity of the general problem is NP-complete. Motivated by this fact and that 2D suffix tries can only give information about square shaped matches, we have considered the performance of greedy parsing with square matches, and have introduced a modified parsing strategy that searches for rectangular matches based on the best square match. We have also introduced multi-shape 2D suffix tries; they are more space consuming but have the ability to store information about arbitrary rectangular shaped matches at any position.
For further information and references see:
-
G. Motta, J. A. Storer, and B. Carpentieri [2000].
"Lossless Image Coding via Adaptive Linear Prediction and Classification",
Proceedings of the IEEE 88:11,
1790-1796.
-
J. A. Storer and H. Helfgott [1997].
"Lossless Image Compression by Block Matching",
The Computer Journal 40:2/3, 137-145.
-
J. A. Storer and H. Helfgott [1997].
"Generalized Node Splitting and Bi-Level Image Compression",
Proceedings IEEE Data Compression Conference, 443.
-
J. A. Storer [1996].
"Lossless Image Compression using Generalized LZ1-Type Methods",
Proceedings IEEE Data Compression Conference,
290-299.
-
C. Constantinescu and J. A. Storer [1995].
"Application of Single-Pass Adaptive VQ to BiLevel Images",
Proceedings IEEE Data Compression Conference,
423.
- See also the paper mentioned earlier that surveys this approach as well as lossy approaches: F. Rizzo, J. A. Storer, and B. Carpentieri [2001]. "LZ-Based Image Compression", Information Sciences.
Digitized video can require over 1 billion bits per second in uncompressed form. We have developed adaptive algorithms for block displacement estimation, which when combined with individual frame compression and lossless post-processing can yield high compression while maintaining acceptable fidelity. Our approach is to adaptively grow and shrink variable size and shaped collections of blocks, called "superblocks". We also consider how parallel mesh architectures can be employed for high speed real time encoding. The first figure below shows the first and last frame of a movie clip and the second figure a "map" (each superblock has been colored with a random color) of how it was partitioned into regions (with a course fidelity setting); the hatched blocks are areas where due to motion in the image, portions of superblocks are splitting off. We have also used image classification algorithms that work off-line on a sub-sampling of the frames to provide information to enhance our on-line algorithm. In addition, we have considered the optimization of codings of this type.

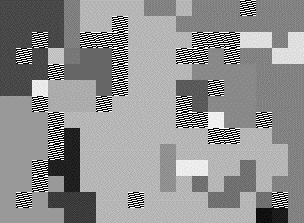
For further information and references see:
-
G. Motta and J. A. Storer [2000].
"An Optimal Frame Skipping Algorithm for H263+ Video Encoding",
Proceedings 11th Annual International Conference on Signal Processing
Applications and Technology,
Dallas, TX.
-
G. Motta and J. A. Storer [2000].
"Improving Scene Cut Quality for Real-Time Video Decoding",
Proceedings IEEE Data Compression Conference,
470-479.
-
B. Carpentieri and J. A. Storer [1996].
"A Video Coder Based on Split-Merge Displacement Estimation",
Journal of Visual Communication and Visual Representation 7:2,
137-143.
-
B. Carpentieri and J. A. Storer [1996].
"Classification of Objects in a Video Sequence",
Proceedings SPIE Symposium on Electronic Imaging,
San Jose, CA.
-
B. Carpentieri and J. A. Storer [1994].
"Split-Merge Video Displacement Estimation",
Proceedings of the IEEE (June),
940-947.
- B. Carpentieri and J. A. Storer [1994]. "Optimal Inter-Frame Alignment for Video Compression", International Journal of Foundations of Computer Science 5:2, 65-177.
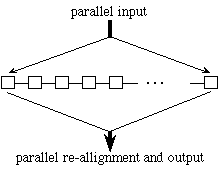
Although adaptive dictionary compression via textual substitution is P-complete (DeAgostino [1994], there are many interesting and practical issues that can be addressed. We have investigated poly-log algorithms for the static-dictionary case. In addition, we have developed fast algorithms for what is perhaps the most practical model of massively parallel computation imaginable: a linear array of processors where each processor is connected only to its left and right neighbors, together with a parallel I/O facility (see the figure below). In other words if one views the PRAM model as having two types of complexity, the inter processor communication and the input-output mechanism, one can view this architecture as having virtually eliminated the complexity of inter-processor communication. Parallel I/O is inherent in any sub-linear algorithm (and makes this model much more powerful than the systolic arrays used for our research on real-time compression).
For further information and references see:
-
D. Belinskaya, S. DeAgostino, and J. A. Storer [1995].
"Near Optimal Compression with Respect to a Static Dictionary on a Practical
Massively Parallel Architecture",
Proceedings IEEE Data Compression Conference,
72-181.
- S. DeAgostino and J. A. Storer [1992]. "Parallel Algorithms for Optimal Compression Using Dictionaries with the Prefix Property", Proceedings IEEE Data Compression Conference, 152-61.
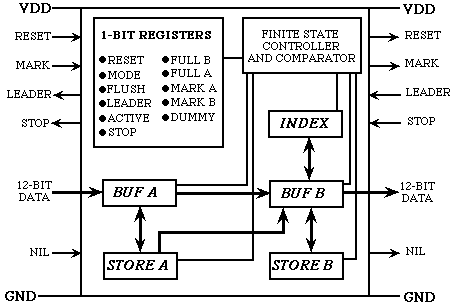
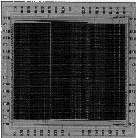
We have studied algorithms for data compression for a systolic pipe; that is, a linear array of processors, each connected only to its left and right neighbors. A real-life example of a systolic pipe is an automobile assembly line that may produce a new car every few minutes even though each car is in the assembly line for a day. Although each station in the automobile assembly line performs a different task, the stations are at least conceptually identical, if we view them all as taking as input a partially built car, performing an elementary operation (such as welding), and then outputting a partially completed car to the next station. From the point of view of practical VLSI implementation, a systolic pipe is very desirable - all processors are identical, connections between adjacent processors are short, the structure can be laid out in linear area, power and ground can be routed without crossing wires, and the layout strategy can be independent of the number of chips used (a larger pipe can be obtained by placing as many processors as possible on a chip and then, using the same layout strategy, placing as many chips as possible on a board). In addition, it is typical for processors to be extremely simple (e.g., a few registers, a comparator, and some finite-state logic). For a variety of textual substitution methods, and have designed and fabricated massively parallel systolic hardware for high bandwidth real-time adaptive dictionary compression. The first figure below shows the layout of an individual processor and the second shows on the left a prototype chip containing 128 processors and on the right 30 chips on a VME board (30 instead of 32 are needed for a 4K dictionary because 256 virtual entries correspond to the raw byte values). The design is inherently fast because all processors compute simultaneously; a clock cycle needs to only be long enough for a individual processor to receive 12 bits and make a 24-bit comparison (there is no global memory or communication). With year 2000 technology, 4K processors can be placed on a single chip that forms a 4K array that can compress or decompress at over a billion bits per second with only an 8-bit data path.

For further information and references see:
-
J. A. Storer and J. H. Reif [1992].
"A Parallel Architecture for High Speed Data Compression",
Journal of Parallel and Distributed Computing 13 ,
222-227.
-
D. M. Royals, T. Markas, N. Kanopoulos, J. A. Storer and J. H. Reif [1993].
"On the Design and Implementation of a Lossless Data Compression
and Decompression Chip",
IEEE Journal of Solid-State Circuits (September) ,
948-953.
-
J. A. Storer [1992].
"Massively Parallel Systolic Algorithms for Real-Time Dictionary-Based Text
Compression",
Image and Text Compression,
Kluwer Academic Press,
159-178.
-
J. A. Storer, J. H. Reif, and T. Markas [1990].
"A Massively Parallel VLSI Design for Data Compression
using a Compact Dynamic Dictionary",
Proceedings IEEE VLSI Signal Processing Conference, San Diego, CA,
329-338.
-
J. Storer and J. H. Reif [1990].
"A Parallel Architecture for High Speed Data Compression",
Third Symposium on the Frontiers of Massively Parallel Computation,
College Park, Maryland, IEEE Press,
238-243.
- M. Gonzalez and J. A. Storer [1985]. "Parallel Algorithms for Data Compression", Journal of the ACM 32:2, 344-373.
Textual substitution methods parse a string into phrases and replace those phrases with pointers to copies, called targets of the pointers, that are stored in a dictionary. The encoded string is a sequence of pointers (some of which may represent single characters). Static methods are when the dictionary is known in advance. By contrast, with dynamic or adaptive methods, the dictionary may be constantly changing as the data is processed (these methods are often called "LZ2" methods due to the work of Ziv and Lempel [1978], and are somewhat different from sliding window methods, which are often called "LZ1" methods due to the work of Lempel and Ziv [1977]). Ziv and Lempel [1978] investigated the encoding power of a finite state one-way head machine with an unrestricted decoder and showed for each individual sequence an asymptotically attainable lower bound on the achievable compression ratio. Furthermore, they achieved this lower bound with an encoder/decoder pair where both are finite state one-way head machines (the LZ2 algorithm), proving that imposing this condition only on the encoder does not lead to better compression. Sheinwald, Lempel and Ziv [1995] show that the same asymptotically attainable lower bound holds when the encoder is unrestricted and the decoder is a finite state one-way head machine, proving that imposing this condition only on the decoder does not lead to better compression either. Hence, off-line encoding for on-line decoding is not more powerful with respect to asymptotic results for infinite strings from an information source (under some information-theoretic assumptions). We are interested in the power of off-line decoding for on-line decoding in the finite case. This models situations such as distribution of data on CD-ROM where much time can be spent encoding but decoding must be fast and simple. We have introduced the notion of on-line decodable optimal parsing based on the parsing defined by the LZ2 algorithm and have shown that optimal off-line encoding is NP-complete for both the original LZ2 technique and for some widely used practical implementations (e.g., first-character learning and next-character learning). We have also shown that approximation algorithms for these problems cannot be realized on-line.
For further information and references see:
-
Chih-Yu Tang and J. A. Storer [2009].
"Network Aware Compression Based Rate Control for Printing Systems",
Proceedings 10th International Symposium on Pervasive Systems (ISPAN 2009),
Kaohsiung, Taiwan,
123-128 (coauthored with Chih-Yu Tang).
-
J. H. Reif and J. A. Storer [2001].
"Optimal Encoding of Non-Stationary Sources",
Information Sciences 135,
87-105.
-
S. DeAgostino and J. A. Storer [1996].
"On-Line versus Off-Line Computation in Dynamic Text Compression",
Information Processing Letters 59,
169-174.
-
J. A. Storer [1991].
"The Worst-Case Performance of Adaptive Huffman Codes",
Proceedings IEEE Symposium on Information Theory,
Budapest, Hungary.
-
J. A. Storer [1985].
"Textual Substitution Techniques for Data Compression",
Combinatorial Algorithms on Words,
Springer-Verlag,
111-129.
-
J. A. Storer and T. G. Szymanski [1982].
"Data Compression Via Textual Substitution",
Journal of the ACM 29:4,
928-951.
- J. A. Storer [1983]. "An Abstract Theory of Data Compression", Theoretical Computer Science 24, 221-237.






































