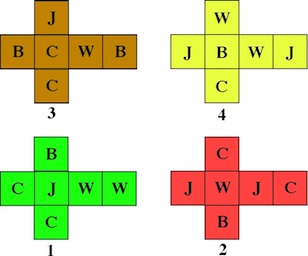
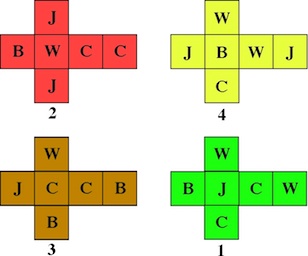
Based on a puzzle produced in 1899; this version made by J. A. Storer, 2011.
(plastic box 1.5" x 2.5" x 3.3", instruction card,
and four 1+3/16" painted wood blocks with vinyl stickers)

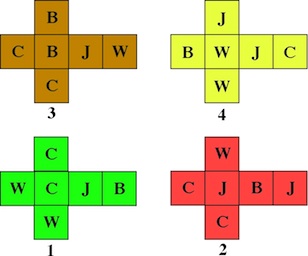
Arrange the cubes in a 2x2 array so that all four letters appear on the top and bottom faces, all four letters appear on the left and right sides, and all four letters appear on the front and back sides. The letters are based on the names of two Boer generals, Joubert and Cronje, and two British generals, Buller and Warren, from an 1899 production of this puzzle.

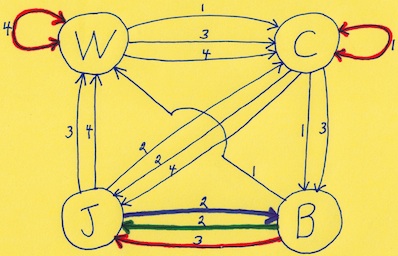
We begin with a different puzzle; here the graph constructed as for Instant Insanity; we use letters to label faces and number the cubes 1 = green, 2 = red, 3 = brown, and 4 = yellow:


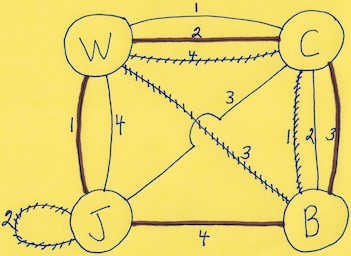
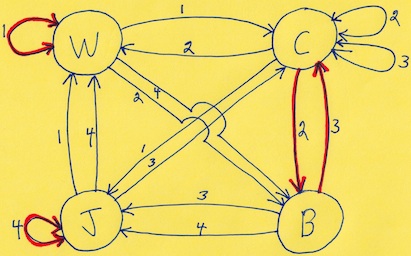
The two cycles, labeled by the thick edges and the hashed edges, give the following instant insanity like solution to arranging the cubes in a 1x4 array so that all for sides show the 4 letters; note that unlike the solution for instant insanity, one of the Hamilton cycles is actually a set of two cycles, a self loop and a cycle of three vertices:

cycle set 1: (J - 1 - W - 2 - C - 3 - B - 4 - J) cycle set 2: (J - 2 - J) (C - 1 - B - 3 - W - 4 - C)

Solution idea: Unlike instant insanity, the graph of the preceding page does not give us a complete solution, because we cannot use disjoint cycle sets to simultaneously set both the top / bottom faces and the sides. Instead, we use each cycle set for a way to set the top / bottom faces that may lead to one or more complete solutions, by searching a new graph that describes the ways that cubes can be in a 2x2 array without changing the top / bottom faces. These secondary graphs are constructed below by going around the sides of each cube in a clockwise direction, where when we go from face X to face Y, we place a directed edge (an edge with an arrow) from vertex X to vertex Y (a total of 16 edges). We now look for cycle sets, but with the rule that the direction of arrows must reverse when going from one cube to an adjacent cube, or stay the same when skipping a corner (that uses a self-loop) and going to the opposite corner.

Solutions based on cycle set 1: Cubes 1 (green) and 4 (yellow) form self-loops; if they are adjacent then the red and green edges can be used to cycle between cubes 2 and 3, and if they are diagonally opposite, then the red and blue edges can be used to cycle between cubes 2 and 3. In both cases, and alternate solution can be formed by exchanging cubes 1 and 4:
Solutions based on cycle set 2: We find a solution based on self-loops for cubes 1 and 4 when they are diagonally opposite (and an alternate solution exchanges cubes 1 and 4):

Further Reading
Boer Wars Wikipedia Page, from: http://en.wikipedia.org/wiki/Boer_war