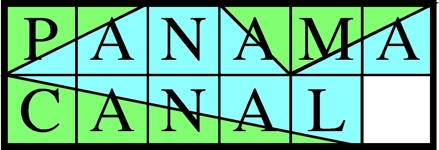
Panama Canal Puzzle




Copyright S. S. A. Co., 1915.
(1.75"x4.75"x7/16" cardboard box and 12 wood pieces with paper glued to top;
directions are on the inside of the box lid)
Starting with the P and C exchanged, slide the pieces to put them back.
A parity argument
(like that for the
Fifteen
puzzle)
might lead one to think that a solution is not possible.
However,
the second and fourth squares of PANAMA can be exchanged without significantly changing the look of the picture formed by the pieces
(if one ignores the background graphics, then shorter solutions are possible - see next page).
Panama Canal Solution
Panama Canal:
Here is a 32 move solution,
where 1, 2, 3, 4, 5 represent the five A's, and X, Y represent the two N's.
If a piece can push other pieces, then this solution can be converted to 21 moves by combining steps
1/2, 8/9/10, 12/13/14, 16/17, 21/22, 28/29/30/31/32.
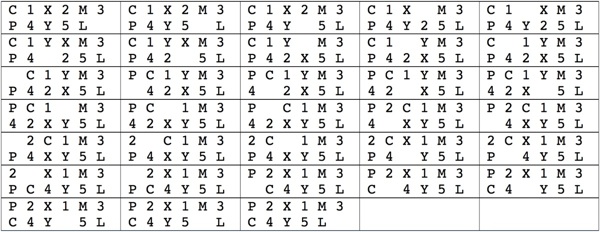
Panama Canal NB:
For the simpler problem with no background,
here is a 26 move solution.
If a piece can push other pieces,
then this solution can be converted to 17 moves by combining steps
1/2/3/4, 8/9, 15/16, 22/23/24/25/26.
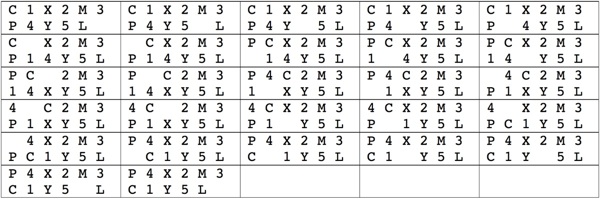
Panama Canal H:
For the even simpler problem with no background and "CANAL" can be right justified,
Hordern's book
gives a 23 move solution and
Baxter's Page
lets one search for a 21 move solution.
If a piece can push other pieces,
then this solution can be converted to 16 moves by combining steps
1/2/3/4, 8/9, 15/16.
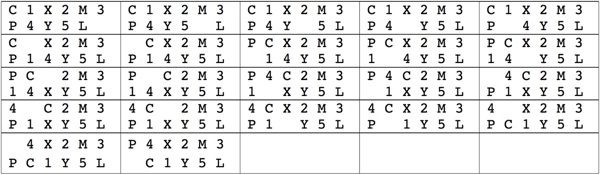
Another Version Of The Panama Canal Puzzle

Designed and made by J. A. Storer 2007.
(3"x 7" x 1.4" wood box, 11 wood pieces, and a black wood keeper piece)
Panama Canal S:
In this version,
the second and sixth squares of PANAMA can be exchanged without changing the picture.
Here is a 48 move solution.
If a piece can push other pieces,
then this solution cab be converted to 36 moves by combining steps
6/7, 11/12, 16/17/18, 20/21/22, 24/25, 29/30, 36/37/38/39, 43/44.
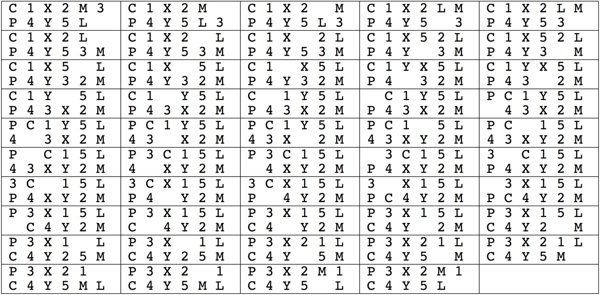
This version does a reasonable job of "exercising" the pieces.
Since half of the possible positions are duplicates due to the two A's with the same background,
there are 12! / 2 = 239,500,800 distinct positions.
To find a solution, a computer program performing a simple breadth-first search visited 102,714,408 positions
(43 percent).
In contrast, the program visited 3,611,235 positions
(1.5 percent)
to solve the standard version,
and for the NB and H versions, where the five A's are interchangeable and the two N's are interchangeable,
giving 12! / 5! / 2 = 3,991,680 distinct positions, to find a solution it visited 120,542 positions (3 percent)
and 42,602 positions
(1 percent)
respectively.
Related Puzzles
The 2-unit high shape has been used in similar puzzles.
The 1923
Hartman patent
shows the same puzzle but with the numbers 1 to 11 on the pieces
(and the goal is to rearrange them so each column sums to 11).
The puzzle below,
purchased in 2008,
has a 2 by 7 array of pieces and an extra position
(similar to the
Sixteen
puzzle):

Further Reading
Baxter's Page,
from: http://www.johnrausch.com/SlidingBlockPuzzles/classic.htm
Hartman Patent,
from: www.uspto.gov - patent no. 1,464,424










