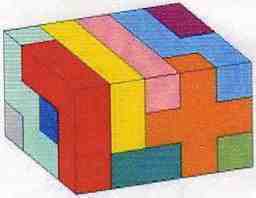
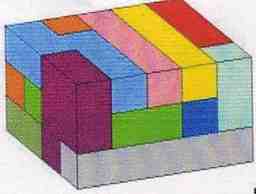
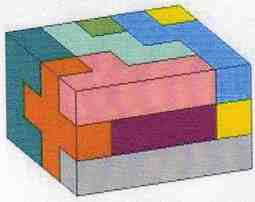
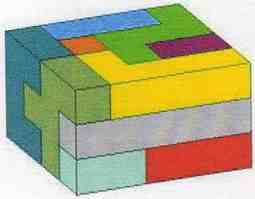
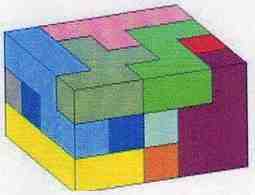
Pentominoes

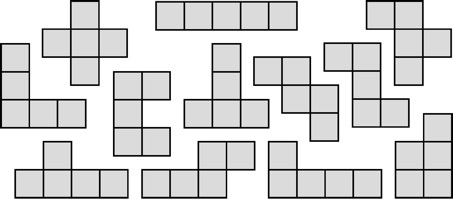
a.k.a. Polyominoes
Old puzzle, this one made by Yasumi, 1995.
(wood, box and 12 pieces based on 0.75" inch cubes)
The 12 distinct shapes formed from 5 connected squares are the pentominoes
(called polyominoes by Solomon W. Golomb, Charles Scribner's Sons, NY, 1965):
Total area is 60, and sizes 6 x 10, 5 x 12, 4 x 15, and 3 x 20 can be formed.
There are known to be 2,339 distinct ways to form a 6 x 10 rectangle,
excluding rotations and reflections.
In contrast, there are 1,010 solutions for 5x12,
368 solutions for 4x15,
and 3 x 20 has a unique solution except for rotating a central portion by 180 degrees.
A piece is landlocked if it does not touch one of the borders of the rectangle.
Eric Harshbarger has determined that there are no 6x10 rectangle solutions with 5 or more landlocked pieces,
but there can be solutions with 0, 1, 2, 3, or 4 landlocked pieces
(e.g., there are 207 solutions of the 6x10 rectangle with four landlocked pieces,
1,111 with three, 864 with 2, 155 with one, and only a couple with zero).
R. M. Robinson of the University of California at Berkeley proposed the "triplication problem":
Given a pentomino, use 9 of the other pentominoes to construct a scale model,
3 times as wide and 3 times as high as the given piece (all 12 are possible).
Pentominoes are traditionally flat pieces that can be arranged to form 2-dimensional patterns.
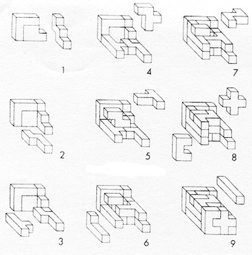
However, if the pieces are made to be 1-unit thick, then fun 3-dimensional patterns can also be made,
including a 3 x 4 x 5 solid, and stairs that are 6 wide by 4 deep by 4 high.
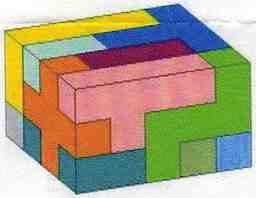
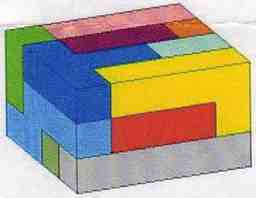
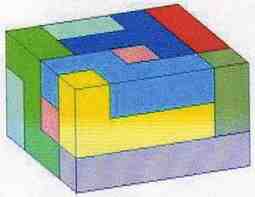
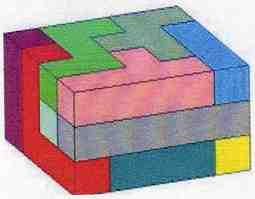
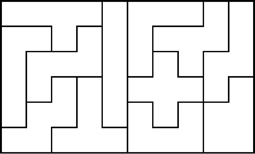
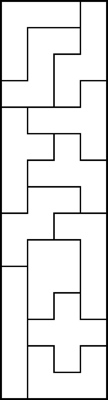
Some Other Pentominoes 6x10 Solutions
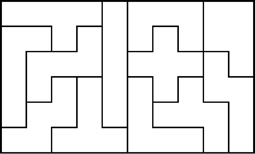
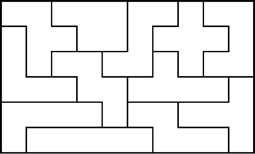
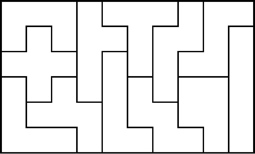
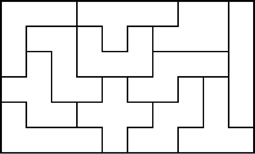
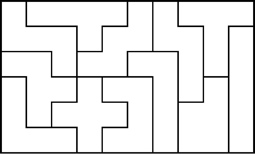
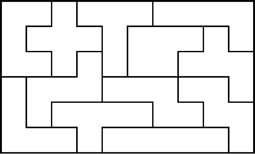
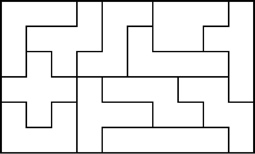
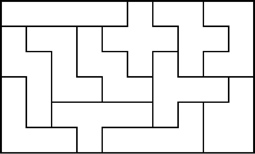
Example Pentomino Solutions That Are Not 6x10
(The shaded area of the 3x20 solution may be rotated by 180 degrees.)
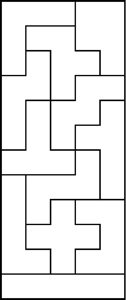

Some Pentomino 3x4x5 Solutions
From the directions sold with the Yasumi version:
From the directions sold with the Interlocking Puzzles version:
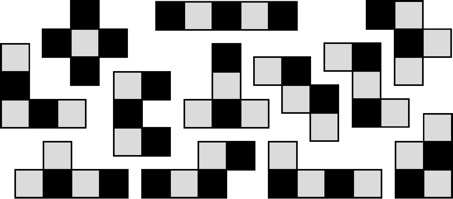
Pentomino Checkerbox:


Made By B. Cutler, 1989.
(3.25"x4"x2.375" plastic box and 12 two-color wood pieces with 3/4" cubes)
Can be used like any other pentominoes set.
In addition, it is made from light and dark woods so that it can be solved in a 3x4x5 box where colors have a checkerboard pattern on all sides.
Here is the diagram of the pieces from the directions that came with the puzzle:
Sold with this puzzle was printout of a number of solutions.
Here is the one suggested;
the pieces have the names 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C,
and this figure shows the three planes of the checkerbox:
ABB5C A666C A636C
BB555 A7778 3333C
B9958 A9778 9944C
11111 22228 44428
Pentomino Rectangular Shapes With Holes
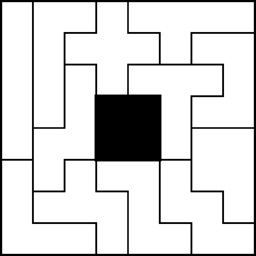
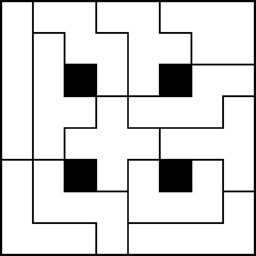
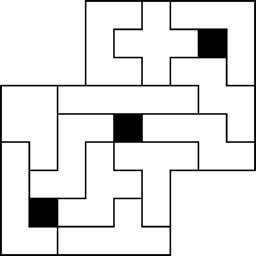
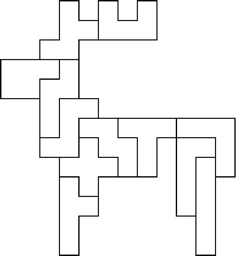
Other Fun Pentominoes Shapes
From the directions sold with the Yasumi version:
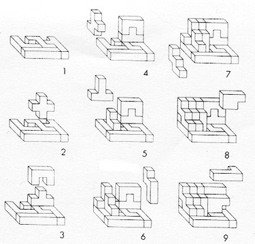
Shown on Nivasch's Page:
Further Reading
Harshbarger's Page,
from: http://www.ericharshbarger.org/pentominoes
Mathworld Page,
from: http://mathworld.wolfram.com/Pentomino.html
CIMT Page,
from: http://www.cimt.plymouth.ac.uk/resources/puzzles/pentoes/pentoint.htm
Gerard's Page,
from: http://www.xs4all.nl/~gp/pentomino.html
Huttlin's Page,
from: http://members.aol.com/huttlin/pentominoes.html
Nivasch's Page,
from: http://yucs.org/~gnivasch/pentomino
Mark's Page,
from: http://mathsevangelist.wordpress.com/2012/08/24/packing-pentominoes
Jankok's Page,
from: http://homepages.cwi.nl/~jankok/etc/Polyomino.html
info Page,
from: http://www.theory.csc.uvic.ca/~cos/inf/misc/PentInfo.html
Gottfriedville Page,
from: http://www.gottfriedville.net/puzzles/colorgame/solutions.htm
Belgium Pentominoe page,
from: http://home.scarlet.be/~demeod/indexe.html
Puzzle Will Be Played page,
from: http://www.asahi-net.or.jp/~rh5k-isn/Puzzle
Fletcher's Page,
from: http://www.andrews.edu/~calkins/math/pentos.htm
Wikipedia Page,
from: http://en.wikipedia.org/wiki/Pentomino
Negahban Design Patent,
from: www.uspto.gov - patent no. 385,311
Further reading about some related puzzles:
Lester Patent,
from: www.uspto.gov - patent no. 1,290,761
Wadsworth Patent,
from: www.uspto.gov - patent no. 3,964,749
Sarkar Patent,
from: www.uspto.gov - patent no. 5,544,882