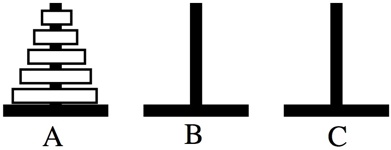
a.k.a. Pyramid Piling Puzzle, Brahma Puzzle
Very old design, this puzzle purchased from Bits And Pieces 2007.
(wood stand and seven wood discs, 2.3" by 5.3" base by 3.5" high)

On Post A there are n rings of different sizes, in the order of the largest ring on the bottom to the smallest one on top. Posts B and C are empty. The object is to move the n rings from Post A to Post B by successively moving a ring from one post to another post that is empty or has a larger diameter ring on top.



Solution: Since any of the rings 1 through n-1 can be placed on top of ring n, all n rings can be moved by invoking the recursive procedure TOWER:

procedure TOWER(n,x,y,z)

if n>0 then begin

TOWER(n-1,x,z,y)
write "Move ring n from x to y."
TOWER(n-1,z,y,x)
end

end

TOWER(n,x,y,z) makes 2ⁿ-1 moves; e.g, TOWER(3,A,B,C) takes 7 steps:


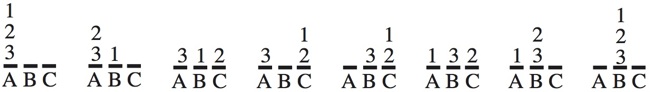
"Unwinding" the recursion of TOWER, yields the following simple iterative algorithm that moves the discs on post in the clockwise direction:

if n is odd then d := clockwise else d := counterclockwise
repeat

Move the smallest ring one post in direction d.
Make the only legal move that does not involve the smallest ring.
until all rings are on the same post

Pyramid Piling Puzzle, Well-Maid Wood Products, Suffield, CT, unknown age.
(cardboard box 3.7" x 5" x 3/4", wood base and pieces, directions, infor. sheet;
the discs were lost at some point and replaced)

Rainbow Puzzle, unknown age.
(2.5" diameter by 1.6" wood box with three 3/16" diameter 2" long wood pegs,
and 8 wood discs, from 11/16" diameter to 1+15/16" diameter;
to play, turn box over and put pegs into the holes in the bottom)


Further Reading
Excerpt from J. A. Storer's book.
Wikipedia Page, from: http://en.wikipedia.org/wiki/Towers_of_hanoi
Wolfram Mathworld Page, from: http://mathworld.wolfram.com/TowerofHanoi.html
Claus Page, from: http://www.cs.wm.edu/~pkstoc/toh.html
Ajtai Patent, from: www.uspto.gov - patent no. 5,992,851