Who's The Boss


Siebenstein - Spiele 2011, Germany.
(wood and plastic, 3.7" x 3.7" x 5/8")
The puzzle works by using your fingers through the four large square holes in the plastic top.
The top is nice for storage and transportation,
but makes it hard to manipulate pieces;
it can easily be temporarily removed for play by undoing the four corner screws
(loosened with a screwdriver in the slots on the back side).
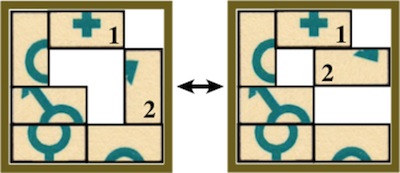
Pieces can be rotated from certain positions.
For example,
from photo 1,
the middle piece alone can be rotated counterclockwise (photo 3) or both can (photo 4):







Three Problems
Problem 1:
Put the female symbols together and leave the other pieces neatly at the bottom:
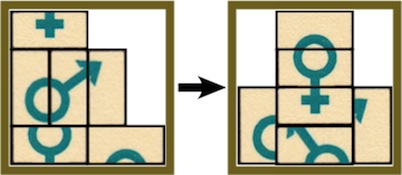
Problem 2:
Put the female symbols together and leave the other pieces in the positions as shown on the directions, in their original orientations:
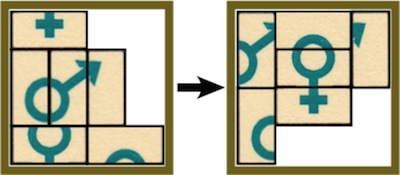
Problem 3:
Put the female symbols together and leave the other pieces in the positions and orientations as shown on the directions:
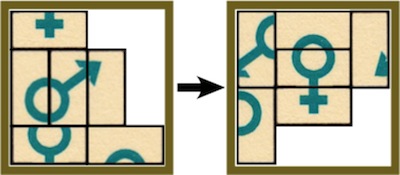
Counting Rotation Moves
For solutions to be presented we charge for rotations as follows:
Type 1:
Any of the 4 variations where block 1 on the left could be positioned 2 units to the left
or block 1 on the right could be positioned 2 units down,
count as 1 move:
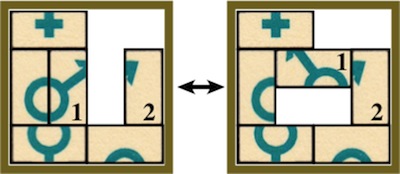
Type 2:
Counts as 2 moves:
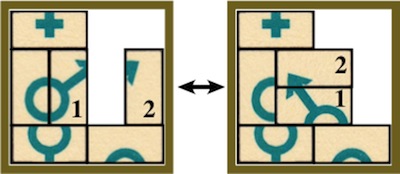
Type 3:
Counts as 1 move:
A Solution to Problem 1
Here is a 23 rectilinear
(29 straight-line)
moves solution that uses only one rotation
(a type 1 rotation at step 2):
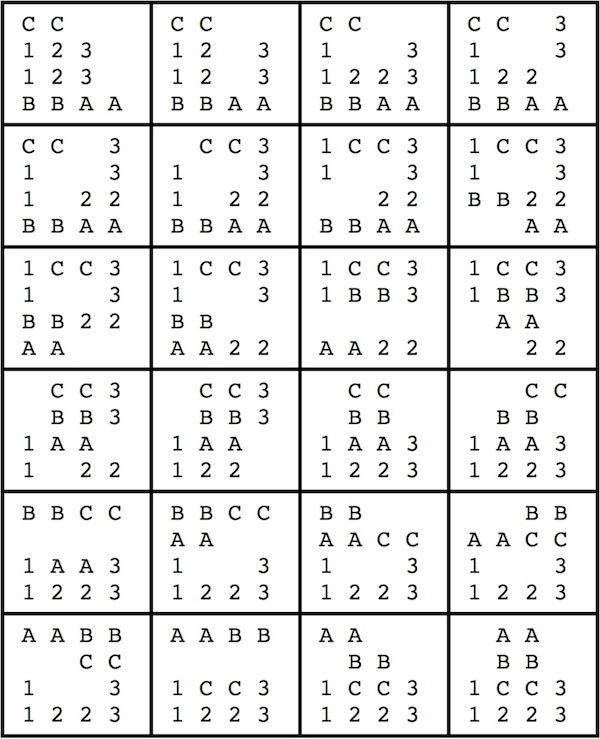
A Solution to Problem 2
Here is a 31 rectilinear
(39 straight-line)
moves solution that uses only two rotations
(a type 1 rotation at step 2 and step 21):
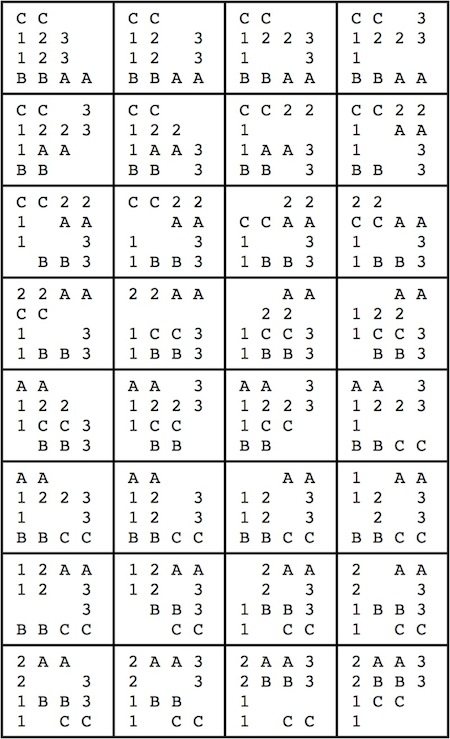
A Solution To Problem 3
Here is a 55 rectilinear
(62 straight-line)
moves solution that uses 5 rotations;
Type 1 at step 47,
Type 2 at steps 2&3 (the two steps represent the cost of 2 for this double rotation),
and Type 3 at steps 11, 20, 43).
This solution does not allow rotation steps to be combine with other steps;
otherwise,
by combining the double rotation steps 2&3 with step 4,
and combining the rotation step 47 with step 48,
this solution translates to 53 rectilinear moves.