

Next: Brassard, Crépeau, Jozsa, Langlois:
Up: Heads or Tails? Quantum
Previous: Quantum Bit Commitment
The famous EPR (Einstein-Podolsky-Rosen) paradox describes a rather counterintuitive
quality of quantum physics: the quantum state space of a set of several particles
is the direct product of their individual spaces, and not the direct sum as
one would expect. As a consequence, if A and B have separate particles
a and b, which happen to be in an entangled state, then
A may be able to gain information on B's measurement of
b by measuring a.
It is possible for A to exploit this in order to cheat. Here's A's
cheating scheme:
- EPR cheating scheme for BB84
- 1.
- Commitment Phase
- A fabricates s pairs of entangled qubits
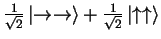 and sends one particle in the pair to B while keeping the other.
and sends one particle in the pair to B while keeping the other.
- 2.
- Disclosure Phase
- A measures her own qubits with respect to basis
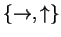 if she wants to disclose a zero and
if she wants to disclose a zero and
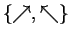 if she wants
to disclose a one. She sends the ``disclosed'' bit along with the results
if she wants
to disclose a one. She sends the ``disclosed'' bit along with the results
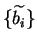 of her measurements.
of her measurements.
A measurement collapses the state of a quantum system into the subspace that
is compatible with the value obtained. A exploits the fact that the state
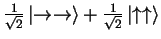 =
=
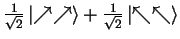 is fully entangled with respect to both bases.
is fully entangled with respect to both bases.
When Alice measures her qubit with respect to the horizontal basis, she gets
either a zero or a one with 50% chance. However, this projects the entire state
space of the entangled pair to either
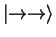 or
or
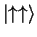 (since the
(since the
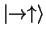 and
and
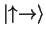 components are zero from
the start), which means that Bob will obtain the same result5. This is exactly the EPR paradox (table 4).
components are zero from
the start), which means that Bob will obtain the same result5. This is exactly the EPR paradox (table 4).
With this procedure Alice makes sure that whenever
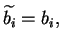 Bob used the same basis to do his measurement, so he will get an identical result.
And in the opposite case, as the angle between state and basis is
Bob used the same basis to do his measurement, so he will get an identical result.
And in the opposite case, as the angle between state and basis is
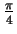 ,
he obtains a 50%-50% distribution as expected.
,
he obtains a 50%-50% distribution as expected.


Next: Brassard, Crépeau, Jozsa, Langlois:
Up: Heads or Tails? Quantum
Previous: Quantum Bit Commitment
1999-11-04
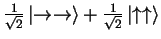 and sends one particle in the pair to B while keeping the other.
and sends one particle in the pair to B while keeping the other.
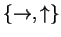 if she wants to disclose a zero and
if she wants to disclose a zero and
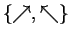 if she wants
to disclose a one. She sends the ``disclosed'' bit along with the results
if she wants
to disclose a one. She sends the ``disclosed'' bit along with the results
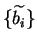 of her measurements.
of her measurements.