Burrs

Pieces are formed by removing unit cubes from rectilinear solid pieces.
A burr is notchable if it can be made with just straight cuts.
Some burrs have a "key" piece that slides out.
More complex ones have a number of internal voids (called holes),
where removing the first piece may require sliding several pieces.
An assembly of a burr is a solved shape.
An assembly is a solution if it can be achieved by starting with the pieces apart and making legal moves.
The level of a solution is the minimum number of moves required to remove the first piece
(or separate the puzzle into two parts).
The level of a burr is the lowest level of its solutions.
Note that to compute level, we use
Cutler's
definition,
where the movement of several pieces together,
or the consecutive movement of pieces in the same direction,
counts as a single "move".
Burr level can be expressed with more than one number;
e.g., 3.7.2 means 3 moves to remove the first piece,
7 moves to remove the second piece,
and 2 moves to remove the third piece.
Standard Six Piece Burrs
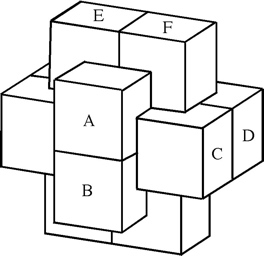
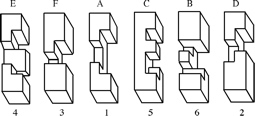
The most well known burr is the standard 6 piece burr,
with 2 x 2 x 6 unit pieces
(or sometimes 2 x 2 x 8).
For example, the figure above shows
Coffin's Improved Burr,
which requires 3 moves to remove the first piece
(letters show how pieces fit, numbers indicate an order in which they can be disassembled).
The number of holes in a standard 6-piece burr:
- Volume of six solid pieces = 6 x 24 = 144 (or 192 for 2x2x8 pieces).
- Volume of a solid burr = 24+24+16+16+12+12 = 104 (or 152 for 2x2x8 pieces).
- Volume difference = 40.
- Holes = (total number of unit cubes removed from the six pieces) - 40.
Standard 6-piece burr records, from the computer work of Bill Cutler:
- Highest level for unique solution with 3 holes = 7.
- Highest level for unique solution with 4 holes = 8.
- Highest level for unique solution with 5 holes = 9.
- Highest level with a unique solution (uses 7 holes) = 10.
- There are no standard 6-piece burrs of level 11.
- Highest possible level (its the only one, but has non-unique solution) = 12.
- Highest level for unique notchable (has 7 holes) = 5.
- Highest level for notchable with non-unique solution = 10.
Example Variations of 6-Piece Burrs
• Fractional or rotation moves.
• Non-rectangular cuts.
• Solutions with exposed holes.
• Ball bearing(s) inside that may have to move during solving.
• Additional moves to remove the second piece require more moves than the first.
Other Types of Burrs:
Non-standard 6-piece burrs have six pieces but don't adhere to standard construction rules.
Burrs in the theme of the standard 6-piece burrs but with more pieces can be difficult,
especially when combined with non-standard constructions.
Burrs with as few as 3 pieces can also be quite difficult
(e.g., the Cuter Level 8
GigaBurr).
Three piece "knots" fit together in a simple but non-obvious way.
Some three piece burrs require unusual twists or diagonal motions.
Burr History
The basic idea of a burr is quite old.
The 1893
Hoffman book
presents a wood knot as "Cross Keys" and a 6-piece burr as "The Nut".
The
Slocum and Botermans New Book of Puzzles,
on page 52 discusses the
Spears Puzzle knots manufactured in Bavaria in 1910 and marketed in England;
it is also mentioned that six piece burrs appeared in Bestelmeier's 1803 Toy Catalog.
The 1929
Johnson and Smith Catalog,
on pages 254-255,
shows a 6-piece burr,
a two burr stick,
and related wood puzzles.
The
Puzzlers' Tribute book,
on page 260 cites a 6-piece burr called the
Devil's Hoof
and a 24-piece burr
called the
Large Devil's Hoof
in a Catel's catalogue of 1785,
and credits David Singmaster's example of a 6-piece burr in a 1733 Spanish book by Pablo Minguet E. Irol;
also, on page 262 it credits the Mikado Puzzle as shown in the 1915 C. J. Felsman Catalogue:

Classic Burrs
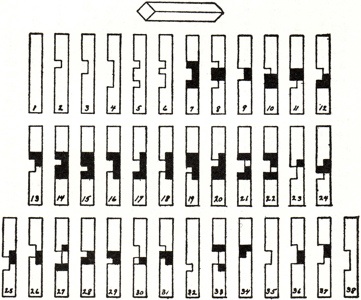
The 1942 Filipiak book has a substantial discussion of burr puzzles;
here are figures it shows of a 3-piece wooden knot,
a 6-piece burr,
and a 6-piece burr set:
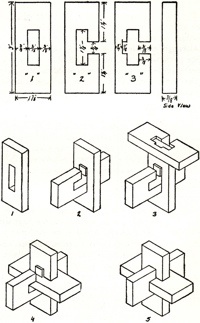
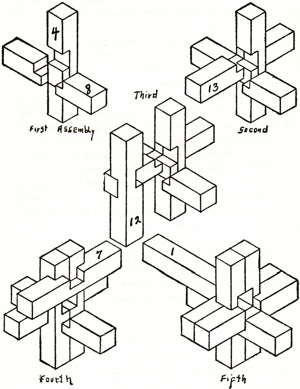
Burr Patents
There have been many burr patents; for example,
here are the figures from the 1890 Altekruse and 1917 Brown patents:
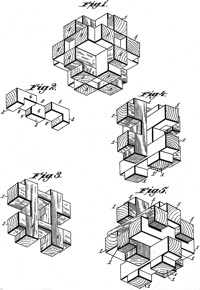
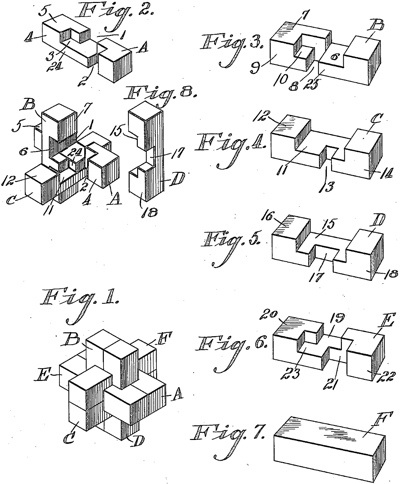
Examples of Burr Patents
Chandler Patent,
from: www.uspto.gov - patent no. 393,816
Altekruse Patent,
from: www.uspto.gov - patent no. 430,502
Porter Patent,
from: www.uspto.gov - patent no. 524,212
Nelson Patent,
from: www.uspto.gov - patent no. 588,705
Ford Patent,
from: www.uspto.gov - patent no. 779,121
Curtis Patent,
from: www.uspto.gov - patent no. 781,050
Erickson Patent,
from: www.uspto.gov - patent no. 985,253
Banic Patent,
from: www.uspto.gov - patent no. 1,099,159
Brown Patent,
from: www.uspto.gov - patent no. 1,225,760
Keiser Patent,
from: www.uspto.gov - patent no. 1,261,242
Senyk Patent,
from: www.uspto.gov - patent no. 1,350,039
Schenk Patent,
from: www.uspto.gov - patent no. 1,455,009
Kramariuk Patent,
from: www.uspto.gov - patent no. 1,542,148
Turner Patent,
from: www.uspto.gov - patent no. 2,836,421
Pidgeon Patent,
from: www.uspto.gov - patent no. 4,148,489
Derouin Patent,
from: www.uspto.gov - patent no. 4,880,238
Dykstra Patent,
from: www.uspto.gov - patent no. 5,040,797
Further Reading
Rob's Puzzle Page,
from: http://home.comcast.net/~stegmann/interlocking.htm
Cutler's Holey 6PB Booklet,
from: http://home.comcast.net/~billcutler/docs/H6PB/index.html
Cutler's Computer Analysis,
from: http://home.comcast.net/~billcutler/docs/CA6PB/index.html
IBM Burr Page
(edited),
from: http://www.research.ibm.com/BurrPuzzles
Curfs' Page,
from: http://home.tiscali.nl/~bcurfs/homepage/burrs/burrs-e.htm
Math Games Page,
from: http://www.maa.org/editorial/mathgames/mathgames_08_02_04.html
Wikipedia Burr Page,
from: http://en.wikipedia.org/wiki/Burr_puzzle
Mathematische Basteleien Page,
from: http://www.mathematische-basteleien.de/devilsknot.htm
Mr. Puzzle Page,
from: http://www.mrpuzzle.com.au/category129_1.htm
Source Forge Page,
from: http://burrtools.sourceforge.net/gui-doc/BurrDesignTools.html









