Chinese Rings

a.k.a. a.k.a. Cardan's Rings, Baguenaudier
Very old design, this one owned by J. A. Storer's grandfather, circa 1900?
(2.4 by 8.5 by 1.75 inches high wood box with key and 6.5 inch long puzzle)
Each ring is attached to a post and,
except for the rightmost ring (the one farthest from the handle),
each goes around the post to its right (and under the ring to its right).
Rings that are not on the skewer can pass sideways through the skewer.
Initially,
the skewer goes through all the rings.
The goal is to remove the skewer from the rings (and then put it back).
Solution:
Observe that the only two ways to move a ring are to put the rightmost ring on or off the skewer,
or,
a ring can be put on or off the skewer if and only if the ring to the immediate right is on but all other rings to the right are off.
This leads to a simple iterative solution in a similar spirit to the
Towers Of Hanoi puzzle;
we use the phrase "complement a ring" to mean take it off if it is on or put it on if it is off:
Take the rings off:
Start with all rings ON.
repeat
Make the only legal move that is not complementing the rightmost ring.
Complement the rightmost ring.
until all rings are OFF
Put the rings on:
Start with all rings OFF.
repeat
Complement the rightmost ring.
Make the only legal move that is not complementing the rightmost ring.
until all rings are ON
The Relationship of Chinese Rings To Gray Codes
Gray codes of n bits are a binary counting system where only one bit changes from the representation
for an integer i to the representation of i+1,
0 &le i &le 2 n - 1.
Let B(i,n) denote the standard binary representation of i using n bits,
G(i,n) the Gray code of n bits,
XOR the exclusive or operation,
and ShiftRight the operation of shifting the bits of a code one position to the right
(discarding the rightmost bit and setting the leftmost bit to 0).
Although Gray codes are not in general unique, a standard form is one where:
G(i,n) = B(i,n) XOR ShiftRight(B(i,n))
Here is the correspondence for n=4;
all 4 bit binary sequences are shown,
but we only need entries 0 through 10:
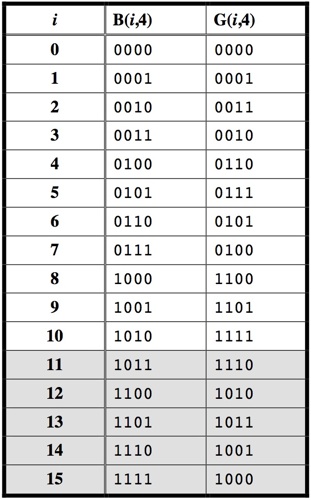
Observe that when going from one row to the next,
every other time it is the rightmost bit that changes,
and for the other times a bit changes where the bit to its right is 1 and all bits to the right of that are 0.
Hence,
if we let 0 denote a ring off and 1 denote a ring on,
then one can see that the Gray code sequence corresponds to our solution for the Chinese rings;
that is,
for the case of 4 rings, taking them off corresponds to moving from row 10 to row 0 in the above table,
and putting them on corresponds to moving from row 0 to row 10.
Number of Moves To Solve The Chinese Rings
The number of moves to put the rings on or off is the same, so let's count the number of moves to take them off.
We can express our iterative solution recursively as follows:
Represent the rings as an array R[1] .. R[n]
where R[1] corresponds to the leftmost ring,
and R[i] is 0 if the corresponding ring is off and 1 if it is on.
Let FLIP(i) denote complementing R[1] through R[i],
then set all positions to 1 and call FLIP(n):
procedure FLIP(i)
if i=1 then Complement R[1].
else if i=2 then Complement R[1] and R[2].
else do
FLIP(i-2)
Complement R[i].
FLIP(i-2)
FLIP(i-1)
end
The number of moves M(n) for FLIP(n) is given by the recurrence relation:
M(n) = M(n-1) + 2M(n-2) + 1
Two simple proofs by induction, one for when n is even and one for when n is odd,
can now be used to show that the solution is:
(2n+1-2)/3 if n if n is even
(2n+1-1)/3 if n if n is odd
The first few values of M(n) are:
1, 2, 5, 10, 21, 42, 85, 170, 341, 682. ...
For the puzzle pictured here, which has seven rings, the solution is 85 moves.
Note:
Sometimes people count the moving of the two rightmost rings as one move, in which case it can be shown that the number of moves is reduced to:
2n-1-1 if n is even
2n-1 if n is odd
And now the first few solution values become:
1, 1, 4, 7, 16, 31, 64, 127, 256, 511, ...
Further Reading
Wikipedia Baguenaudier History Page,
from: http://en.wikipedia.org/wiki/Baguenaudier
Jaap's Page,
from: http://www.jaapsch.net/puzzles/spinout.htm
IES Page,
from: http://www.daviddarling.info/encyclopedia/C/Chinese_rings.html
Jim Loy's Page,
from: http://www.jimloy.com/puzz/chinese.htm
JCKLueng Page,
from: http://staff.ccss.edu.hk/jckleung/ninering/solu_eng.html
Jill Britton's Page,
from: http://britton.disted.camosun.bc.ca/patience/patience.htm
Devil's Halo Page,
from: http://www.puzzlemuseum.com/month/picm05/200501d-halo.htm
Wikipedia Gray Codes Page,
from: http://en.wikipedia.org/wiki/Gray_code
Answers.com Gray Codes Page,
from: http://www.answers.com/topic/gray-code?cat=technology
Wolfram Mathworld Gray Codes Page,
from: http://mathworld.wolfram.com/GrayCode.html
Joyner and McShea Gray Codes Page,
from: http://eng.usna.navy.mil/~wdj/gray.htm
Conrad's Gray Codes Page,
from: http://www.yagni.com/graycode
Everything Gray Codes Page,
from: http://everything2.com/node/114662
PC In Control Gray Codes Page,
from: http://www.pc-control.co.uk/gray_code.htm
Kamruzzaman Gray Codes Page,
from: http://acm.uva.es/p/v104/10455.html
Doran Gray Codes Page,
from: http://members.tripod.com/~rvk/index-2.html
Whealton Gray Codes Page,
from: http://www.washingtonart.net/whealton/gray.html
Sluss Patent,
from: www.uspto.gov - patent no. 3,784,206
Guindon Patent,
from: www.uspto.gov - patent no. 6,508,467

