Trap

Designed by Minoru Abe 1986, this one made by J. A. Storer 2008.
(cardboard sleeve, cherry tray 4" x 5" x 5/8", 12 metal 1/4" thick pieces
with plexi-glass keeper;
left half is aluminum and right half is brass)
There are four 1x2 rectangles,
two 1x1 squares, and six 5/8x5/8 little squares labeled
1, 2, P, A, R, T;
each little square is larger than 1/2 unit on a side
(so that two little squares cannot pass each other in 1 unit wide opening).
The rectangles have receptacles into which a little square can
(fit but not a 1x1 square).
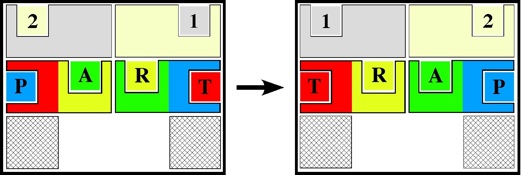
The goal is to start with it reading
2 1 P A R T
and slide the pieces to make it read
1 2 T R A P,
where the rectangles end up in the same positions as they started
(piece coloring is decorative to emphasize the solved state).

Hordern's book
gives a solution of 177 rectilinear moves
(196 straight-line moves), where a rectangle moving with little squares in its recepticle(s) counts as one move.
Baxter's Minoru Abe Gallery
indicates a solution of 174 rectilinear moves
(which he has credited to
Jim Henderson),
which can be achieved by a slight modification to Hordern's solution.
Those who enjoy this puzzle should also try the
Tricky
puzzle.
Further Reading
Baxter's Abe Gallery,
from: http://www.johnrausch.com/SlidingBlockPuzzles/gallery.htm
A Commercial Version Of Trap

Purchased 2012.
(wood tray and pieces in cardboard box, 5.4" x 6.375" x 7/8")
Hordern's Trap Solution Idea
Hordern first determines the positions that allow one to exchange a pair of little squares,
and finds that there are six possible exchanges that can be performed
(there are six positions each for performing the 1<->P and 2<->T exchanges,
whereas the other four each have a unique position in which they can be performed):
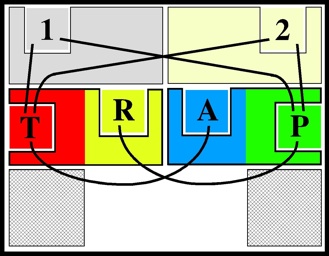
Solving amounts to planning a sequence of exchanges.
Hordern finds that
nine exchanges
are needed,
and gives a basic argument that 7 exchanges suffice to get A and R to their correct positions,
where some ways of doing this need only two additional exchanges to fully solve the puzzle.
He then finds that it takes between 7 and 27 moves to go between any one exchange position and another,
notes that there are several orderings for nine exchanges that use a total of 179 moves,
and presents this 177 move solution:

Partial Capture Moves:
A little square can move
(when there is room to move)
by placing a finger on it and sliding it.
This is also true of rectangle.
However,
if it is desired that a rectangle move so as to carry along with it the little square(s) it contains,
it may be necessary to place a finger on a little square so that pushing it
also results in pushing the entire assembly without a little square being left behind.
Allowing such
partial capture moves
can save a move.
Hordern's Trap Solution Basic Steps
Below are the start and end positions and each of the nine positions that Hordern's solution visits to exchange a pair of little squares.
The larger pieces are labeled
M, N, V, W, X, Y.
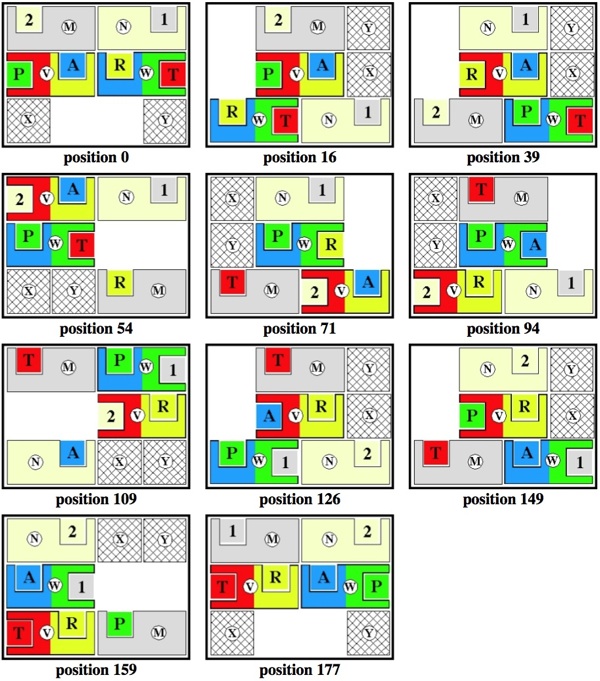
The Complete 177 Move Hordern Trap Solution
We use a more verbose notation than
Hordern's book.
The first letter is the piece to be moved and the second letter is the direction;
all moves are a distance of 1 unit unless followed by a 2 (to specify two units).
Two consecutive moves of the same piece are listed together as a single rectilinear move.
The little squares are denoted 1, 2, T, R, A, P,
the two top rectangles by M and N,
the two middle rectangles by V and W,
and the two bottom large squares by X and Y.
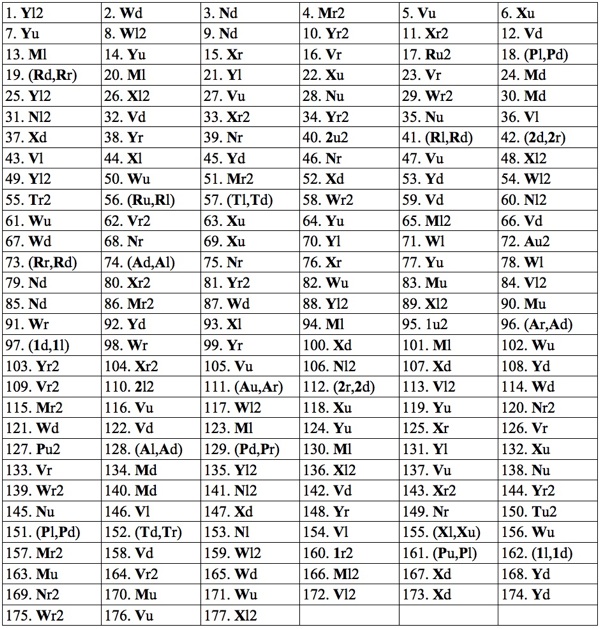
(177 rectilinear moves, 196 straight-line moves)
Reducing Hordern's Solution by Two Moves
A two move reduction can be achieved by changing what happens at position 54
to accomplish the effect of the four moves 55 through 58 in three moves
(left below)
and also at
(now)
position 108 to accomplish the effect of the four moves 109 through 112 in three moves
(right below):
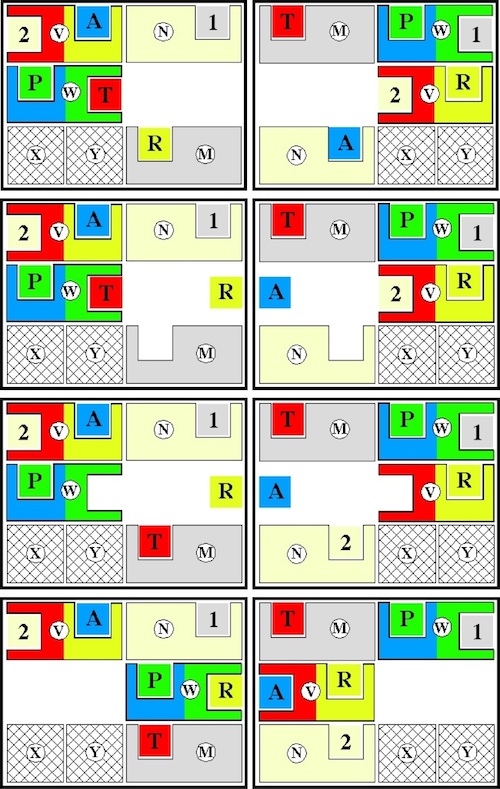
Reducing Hordern's Solution by Three Moves
An additional move can be saved by using a partial capture move for exchange 9.
As shown here, partial capture moves can also be used for exchanges 3 and 6
(but are not necessary for those exchanges,
which can instead be done in the same number of moves by employing a capture move that slides over a small square).
Below are the start, end, and each of the nine positions where an exchange occurs.
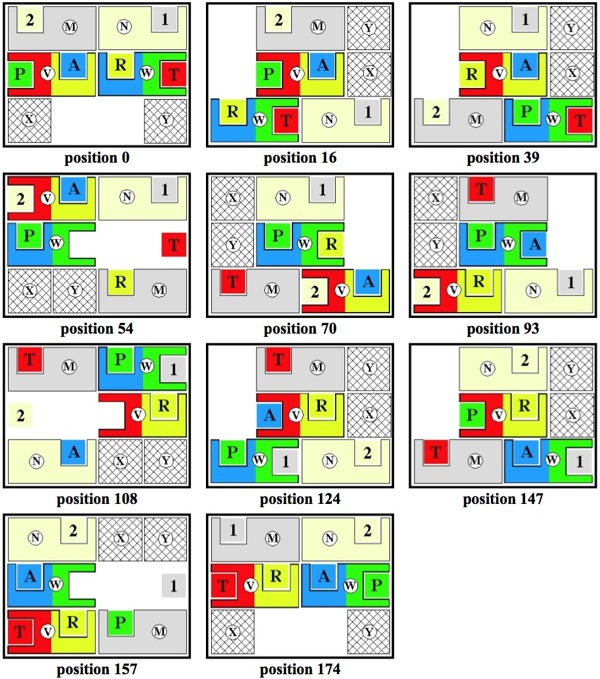
The Complete 174 Move Modified Hordern Trap Solution
For a
174 rectilinear moves
solution,
we again use a more verbose notation than Hordern's book.
The first letter is the piece to be moved and the second the direction;
all moves are a distance 1 unless followed by 2
(moves of a little square by a non-integral distance less than 2 count 1 unit).
Two consecutive moves of the same piece are listed together as a single rectilinear move.
The little squares are denoted 1, 2, T, R, A, P,
the two top rectangles by M and N,
the two middle rectangles by V and W,
and the two bottom large squares by X and Y.
In addition / means do not move that letter;
e.g., Wl2/T
means move W left two units but without dragging the T with it.
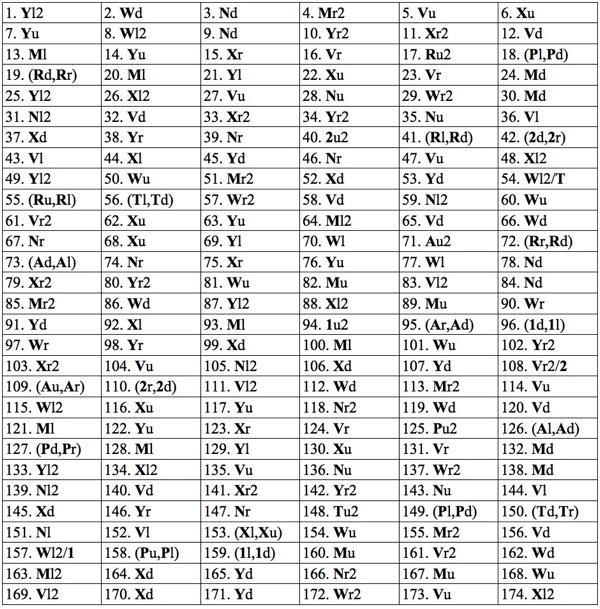
(174 rectilinear moves, 193 straight-line moves)
The Trap 174 Move Solution Vs. 175 Move Solution
Define a
partial capture move
as one where the capture piece slides away from a captured piece and leaves it behind,
and a
catch capture move
as one where the capture piece slides over a piece at the end of its move to capture that piece.
Computer simulation of Hordern's solution computed a solution of
175 rectilinear moves
that uses only catch capture moves for exchanges and no partial capture moves.
That solution can be reduced by one move to
174 rectilinear moves
by using a partial capture move for the final exchange.
In the output shown below for exchange 9 of the 175 move solution,
move 157 can use a partial capture move to leave piece 1 behind,
and move 158 can be eliminated
(position 159 now has piece 1 at the middle right, and move 60 can move piece 1 into piece M):













