Designed by Minoru Abe 2008,
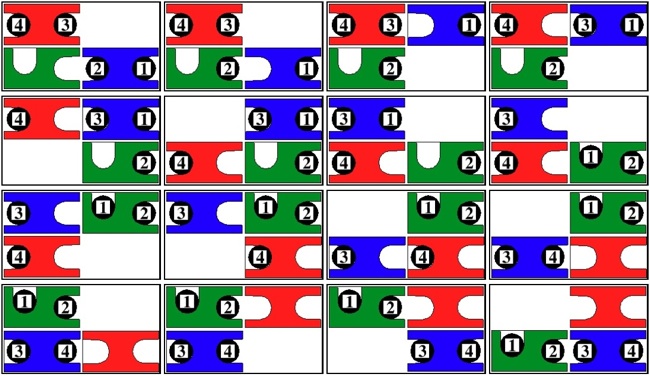
left made by J. A. Storer 2009, right purchased in Japan 2010.
(left: Cherry tray with 1/2 inch thick Walnut and aluminum pieces, 4.5" x 7.5" x 1",
right: wood tray, 7 wood pieces, and a wood keeper, 3.3" x 4.7" x 3/4")

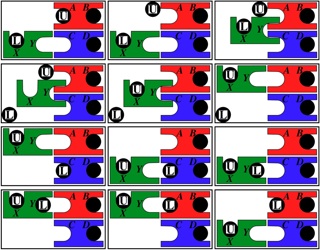
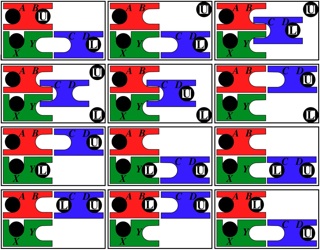
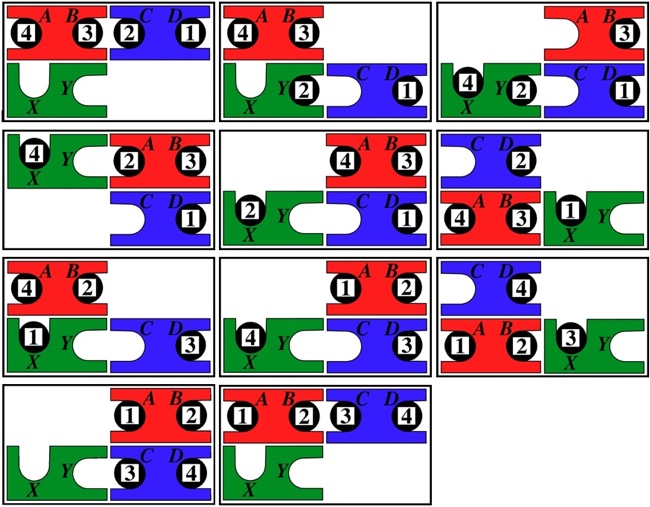
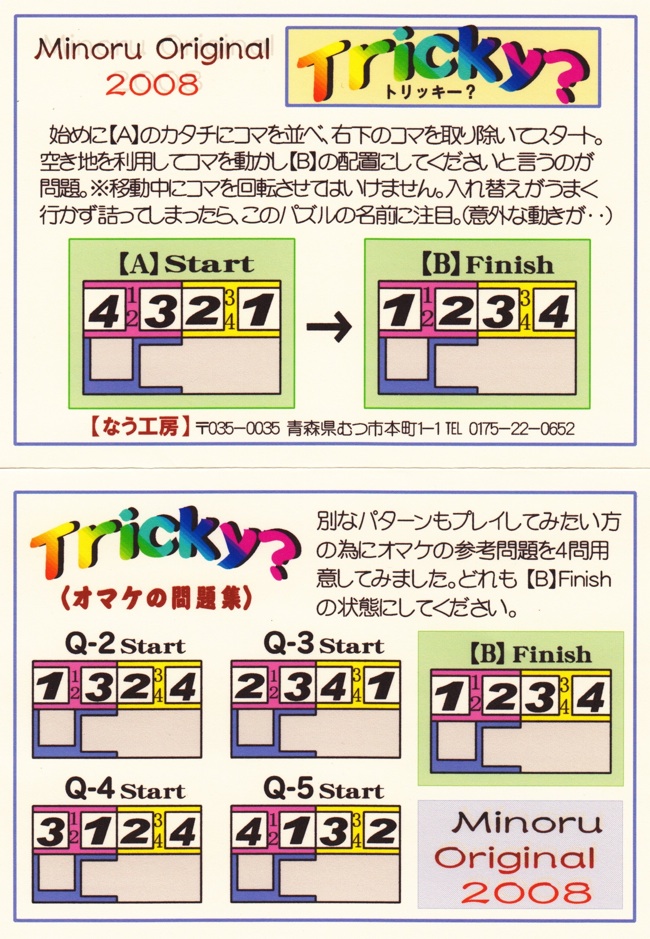
A smaller puzzle in the theme of Trap, where here both exchanges and transfers are possible. The Abe puzzle instructions present five problems for arranging the numbers so they read 1-2-3-4 from left to right, the first of which is starting with them in the order 4-3-2-1 as shown on the right above (the other four are to start with 1-3-2-4, 2-3-4-1, 3-1-2-4, or 4-1-3-2). All five problems require that the blocks end up in their original positions (next page). It is a good warm up exercise to first ignore this requirement and solve the easier problem to read 1-2-3-4 on the bottom; starting with the position on the right above, here is a way to do that in 16 moves, using only transfer operations:

Call operations that move discs when the blocks are positioned in three of the four quadrants as "standard operations". Here is a map of the possible standard operations, where a line goes between two places if a transfer can be made and a line has double arrows if an exchange is also possible, where an s next to the line indicates that the exchange is possible for the version made by J. A. Storer shown on the previous page (the "disc version") but not in the Abe version (which instead of discs has little squares of a slightly larger relative size):



Rearranging to 1-2-3-4 is not possible using only the standard operations (there is no way to get 3 out of the way to clear a path for 2). Key are trick operations where, when positions C and Y are empty, an upper and lower disc can exchange places by circulating around a block:

Left Trick

Right Trick

Here are basic solution steps (red, blue, and green denote a move of the blocks that start in the upper left, upper right, and lower left respectively):

1.   blue, 2 -> Y (transfer - 1 move)
2.   red, 4 -> X (transfer - 1 move)
3.   green, 2 -> A (transfer - 1 move)
4.   green, 2 <=> 4 (left trick - 5 moves)
5.   red, blue, green, red, blue, 2 <-> 1 (standard exchange - 3 moves)
6.   blue, red, green, blue, 2 <=> 3 (right trick - 8 moves)
7.   red, 1 <=> 4 (left trick - 5 moves)
8.   red, blue, green, red, blue, 3 <-> 4 (standard exchange - 3 moves)
9.   blue, red, green, blue, red, 3 => C (partial left trick - 7 moves)
10.   red, blue

The following two pages show how to implement a left trick with 5 moves, a partial left trick with 7 moves, and a right trick with 8 moves, for a total of 60 moves (or 56 moves for the disc version if the two left tricks are replaced with a standard exchange of 3 moves).

A sequence of 11 rectilinear moves can be used for a left and right trick in an approximately symmetric fashion; they are the same for the Abe and disc versions, except that for the disc version the central block (green for a left trick or blue for a right trick) is vertically centered at step 2, whereas in the Abe version, it is all the way in and shifted down as much as possible):

Left Trick

Right Trick

N. Baxter has observed that the number of moves for both tricks can be reduced. The left trick is 5 moves by not circulating disc L and employing a move that drags the green block by pushing disc U, and the right trick is 8 moves by a highly non-rectilinear move of the blue block that detaches from disc L and captures disc U:

Left Trick: 1. U comes out of the red block. 2. Green goes to the trick position. 3. L goes up to the upper left corner. 4. U goes into the green block     and pushes it to the lower left. 5. L goes into the red block.

Right Trick: 1. Disc U goes straight to the right. 2. Blue block moves away from disc L,     captures disc U, and ends in the upper right. 3. Disc L goes into the green block. 4. Blue block moves down. 5. Disc L moves into the blue block. 6. Blue block moves up. 7. Disc L moves into the red block. 8. Blue block moves down.

Although a left trick is possible in the disc version, it is not needed because a standard exchange between positions A and X can be used instead. This additional exchange reduces the number of moves in a solution but does not make achieving 1-2-3-4 significantly easier (since once the right trick is discovered, so will the left trick); in fact, it may make the puzzle a bit harder because initially one may be more likely to think a solution with standard moves is possible.

Returning to the straightforward 11 steps for a left trick, observe that after move 7, disc L is in position C, and with one more move disc U can return to A for the net effect of moving disc L from X to C in 8 moves; we can optimize this to work in 7 moves:

1. Disc 1 comes out.
2. Green block goes to the trick position.
3. Disc 3 moves to the lower left corner.
4. Disc 1 goes into the green block.
5. Green block goes to the upper left.
6. Disc three goes into the blue block.
7. Disc 1 pushes the green block down and then moves into the red block.

Note: The very next move after the partial left trick is to move the red left, so another way to implement step 7 of the partial left trick in this situation is: in move 5 of the partial left trick, do not move the green block all the way up, so now move 7 can move the green block down, leaving disc 1 behind, to be captured by the red block.

Here is the start position and the position after each of the basic steps:

A shorter solution, that works for both the Abe and disc versions, can be achieved by using a different sequence (transfer, transfer, left trick, right trick, exchange, right trick, left trick, transfer) and optimizing local movements. Here are selected positions of this 49 rectilinear (69 straight-line) moves solution; it allows the capability for a piece to leave a captured piece behind during a move, and also to catch one during a move and continue on with it (if this capability is forbidden, then moves 3 and 48 can each be replaced by two moves, for a 51 moves solution).

For the disc version, the solution of the previous page is 46 moves (61 straight-line moves) by saving a move in the sequence at step 14 and saving two more moves in the sequence at step 39. For example, at Step 14, the disc version's ability to directly exchange discs at position A and X, allows us to keep disc 1 with the green block because there will be enough clearance to move it up past disc 2 into the red block.

Here is an equivalent 46 moves solution to that for the disc version on the preceding page; it uses squares of a size smaller than the Abe version (to allow the same clearences as for the discs):