Real world example

Let's now consider how this portfolio algorithm would perform on two real stocks. We'll consider a 22-year period (ending in 1985) of the stock of Iroquois Brands Ltd. and Kin Ark Corp., which were highly volatile during that time period as can be seen in figure .

  

Figure: Performance of Iroquois Brands Ltd. and Kin Ark Corp. stock during the time period from 1963 to 1985.

If an investor would have had access to this information in 1963 he could have earned approx. 791% profit by buying and holding the best stock (Iroquois) which has an ending rate of 8.915 (see figure ).

 

Table: Constant rebalanced portfolio performance of the The Iroquois Brands Ltd. vs. Kin Ark Corp. for different portfolio strategies.

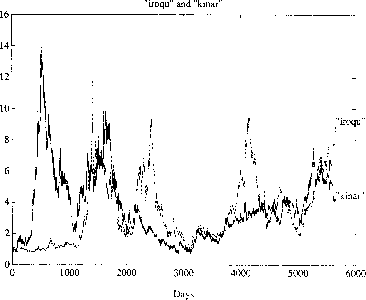
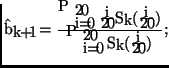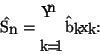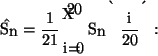b		Sn(b)			b		Sn(b)
1.00		8.9151			0.45		68.0915
0.95		13.7712			0.40		60.7981
0.90		20.2276			0.35		51.6645
0.85		28.2560			0.30		41.7831
0.80		37.5429			0.25		32.1593
0.75		47.4513			0.20		23.5559
0.70		57.0581			0.15		16.4196
0.65		65.2793			0.10		10.8910
0.60		71.0652			0.05		6.8737
0.55		73.6190			0.00		4.1276
0.50		72.5766

 

If we look at the performance of some constant rebalanced portfolios for that period (see table ), we notice that the best rebalanced portfolio is b^* = (.55,.45), which gives us wealth increase of S_n^* = 73.619. This is the target wealth, which we strive to get as close to as possible. To use the universal portfolio algorithm, described in the previous section, we must for quantize all integrals giving us the following equations:

$$S_n^* = \max_{i=0,1,\ldots, 20} S_n(i/20),$$ (26)

$$\hat{b}_{k+1} = \frac{\sum_{i=0}^{20}\frac{i}{20}S_k(\frac{i}{20})}{\sum_{i=0}^{20}S_k(\frac{i}{20})},$$ (27)

and wealth

$$\hat{S}_n = \prod_{k=1}^n \hat{b}_k x_k.$$ (28)

It can be verified that $\hat{S}_n$ can be expressed in the equivalent form

$$\hat{S}_n = \frac{1}{21} \sum_{i=0}^{20} S_n \left( \frac{i}{20} \right).$$ (29)

  

Figure: Performance of the universal portfolio compared to the performance of stocks in The Iroquois Brand Ltd. and Kin Ark Corp.

Using this we can get a universal wealth of $\hat{S}_n = 38.6727$ as can be seen in figure . Even though the universal portfolio gives less wealth then S_n^* it still gives much greater wealth than what an investor could get, when given information n days into the future. Although these results are encouraging, the universal portfolio barely outperforms stocks with a lockstep performance, e.g. the stocks in Coca Cola and IBM.