

Next: Quantum Bit Commitment
Up: Heads or Tails? Quantum
Previous: Quantum Computing
The classical application of cryptography occurs on war or espionage scenarios,
Alice-Eve-Bob, where A needs to send secret information to B over
channels that may be insecure. Other cryptographic problems are sometimes referred
to as ``post-cold-war'', or ``peaceful''. Remote coin tossing is one. Another
example is that of two would-be business partners who wish to know whether or
not their combined capitals are enough for a certain joint venture, without
revealing their individual amounts to each other.
Cryptography research is concerned with finding fundamental operations and protocols
which can be used as building blocks for the more elaborate problems. ``Trap-door''
or ``one-way'' functions for example, which are bijective functions easy to
compute in one direction, but infeasible in the other, allow for the description
of various protocols without dealing with the details of which particular function
one would prefer to use.
Bit commitment (BC) is one such basic protocol which can be used as a foundation
for all the so-called post war cryptography:
- 1.
- Commitment Phase: Alice chooses one bit b, zero or one, in a way that
guarantees to Bob that she has made her decision already and it is not subject
to change. She will probably give Bob some proof of commitment.
- 2.
- Disclosure Phase: Later in time, Alice tells Bob what b was. Bob is satisfied
that this is the same value that b had at the end of phase 1.
A useful analogy for bit commitment is that of a safe box and a key: Alice writes
down her bit in a piece of paper and puts it in a safe box, which she locks.
She gives Bob the box but not the key. For the disclosure stage, Alice gives
Bob the key so he can open the box and verify what the bit was. Since he has
been holding the box all the time, he can be sure that the paper has not changed.
Also, Alice kept the key, so she is sure that Bob was not able to peek inside.
With today's cryptography one would do this using a trap-door function, as in
the following example:
- 1.
- Commitment Phase:
- (a)
- A chooses two large primes, p and q, and reveals n=pqalong with a public k such that
(k,(p-1)(q-1))=1.
- (b)
- A chooses her bit b and a random integer 0<z<n such that
z
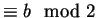 .
.
- (c)
- A broadcasts
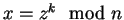 .
.
- 2.
- Disclosure Phase
- (a)
- A reveals b and z
- (b)
- B observes that z
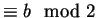 and computes
and computes
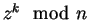 to verify that it equals x.
to verify that it equals x.
Commitments like this are at the heart of many everyday games and business applications.
In an international bid for example, contractors send in their quotations with
the prices they would charge to do some public works enterprise, such as a bridge.
All bids are kept in closed envelopes and open at the same time. The contractor
with the lower price is the one hired for the task. This high-profile protocols
are threatened by espionage, corruption and the like, and the sealed envelopes
are not always that much sealed nor the information they contained is that much
of a constant.
It is easy to define a remote coin tossing protocol if one has a BC protocol
ready:
- Remote Coin Tossing based upon Bit Commitment
- 1.
- Alice chooses a random bit b and commits to it.
- 2.
- Once Bob received a proof of commitment, he chooses a random bit b' himself
and announces it to Alice
- 3.
- b is now disclosed. If b=b' then Bob wins the coin toss, otherwise
Alice wins.
The original Bennett and Brassard protocol for Quantum Bit Commitment (QBC)
was presented as a coin tossing protocol, but can be easily rephrased into the
better known form of bit commitment discussed below.
Yao [20] has shown that a secure QBC can be used to implement a secure
Oblivious Transfer which in turn is a foundation for the more general
problem of Secure Two-party Computation [10], also known
as Discreet Decision Making. Here two parties A and B wish
to compute the value of a function f(x,y) for x known by A
and y known by B, without revealing more information to B(resp. A) than what he can already deduct by knowing
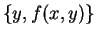 (resp
(resp
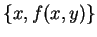 ). The joint capital problem mentioned above is one
of this kind.
). The joint capital problem mentioned above is one
of this kind.


Next: Quantum Bit Commitment
Up: Heads or Tails? Quantum
Previous: Quantum Computing
1999-11-04
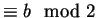 .
.
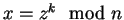 .
.
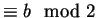 and computes
and computes
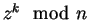 to verify that it equals x.
to verify that it equals x.