Pablo Funes
A certain extraordinarily complicated looking set...
Roger Penrose, The Emperor's New Mind
Complex suggests the unavoidable result of a necessary combining and does not imply a fault or failure <a complex recipe>. Complicated applies to what offers great difficulty in understanding, solving, or explaining <complicated legal procedures>.
Merrian-Webster's Collegiate Dictionary
Complexity is a frequent word in present days' scientific literature, in different fields and with diverse meanings, sometimes appearing as precise concepts and others as vague ideas. We ourselves are part of a multi-disciplinary scientific effort called Center for Complex Systems.
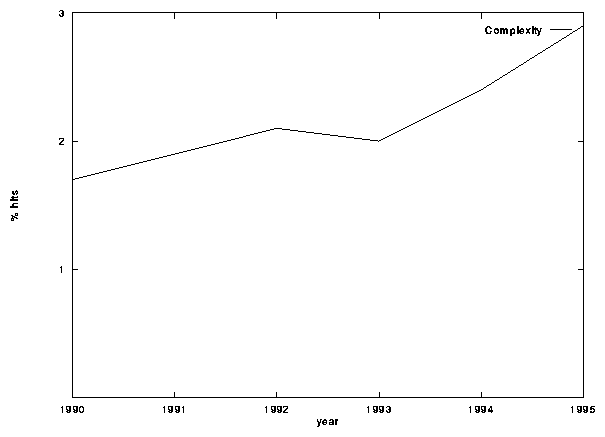
It was our preconception that the term, as happens often with scientific names that spread rapidly from one discipline to others (like chaos in the last decade), would be settling down as its useful niches in different disciplines were found. A naive experiment (fig. 1) suggests that this is not the case, as the appearance of the keyword complexity in scientific literature might have been raising in over the last six years.

The notion of Kolmogorov Complexity studied in our course ([C-T], chapter 7) is very interesting, as it defines a mathematical measurement to how complex a given number or string are, relative to an abstract production system such as a Turing machine.
The cover of our course textbook, Elements of Information Theory ([C-T]), depicts a computer generated image of a small segment of the Mandelbrot set. The explanation on the back cover says "The information content of the fractal on the cover is essentially zero". This comment contradicts our intuitions: The picture looks very complex, as Penrose so vividly expresses it. It is true that the phrase exaggerates as there is more in the picture than just the underlying mathematical formula M= C\{z: |(z+(z+(z+(...+(z+z2)2...)2)2)2)2| > 2}. The corners of the square in the book's cover have been carefully selected because they contain an interesting image.
As a non self-similar fractal, like the border of the Mandelbrot set, endlessly reveals new detail when the resolution is increased, images generated from it can be of any desired Kolmogorov complexity. Two numbers are required to fix a square in the complex plane. As there are rational numbers of any desired complexity, specifying two to fix a square in the Mandelbrot set such as the book's cover can be as complex as desired.
There is another interesting dimension to this problem of
describing small parts of the Mandelbrot set. When the resolution of
an image of the border 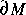 of the set
is increased (i.e., the size of the chosen neighborhood is reduced)
more iterations of the loop are necessary. For every
of the set
is increased (i.e., the size of the chosen neighborhood is reduced)
more iterations of the loop are necessary. For every 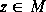 and n there is a δ>0
such that all complex numbers w inside a δ-neighborhood of z remain undecided after n iterations of the loop. As a result, rendering a small part of
and n there is a δ>0
such that all complex numbers w inside a δ-neighborhood of z remain undecided after n iterations of the loop. As a result, rendering a small part of 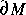 into a picture is an increasingly hard task. This kind of computational complexity is also not considered by Kolmogorov and Chaitin's measure. Our intuitive notion of complexity would acknowledge that these features make M a complex object. Not surprisingly it has received so much attention. On the other hand, objects that are totally random, which have maximum Kolmogorov complexity, are uninteresting. A television set displaying only static noise is not very interesting: It's simple noise, after all. There are ongoing research efforts devoted to find a mathematical definition of complexity that captures these intuitive properties. As we shall see, the task has resulted complex indeed, and no final conclusion has been reached.
into a picture is an increasingly hard task. This kind of computational complexity is also not considered by Kolmogorov and Chaitin's measure. Our intuitive notion of complexity would acknowledge that these features make M a complex object. Not surprisingly it has received so much attention. On the other hand, objects that are totally random, which have maximum Kolmogorov complexity, are uninteresting. A television set displaying only static noise is not very interesting: It's simple noise, after all. There are ongoing research efforts devoted to find a mathematical definition of complexity that captures these intuitive properties. As we shall see, the task has resulted complex indeed, and no final conclusion has been reached.
Science in our century has found, in several different forms, theoretical and practical limits to the capabilities of understanding the laws that rule physical reality and using them for predicting and controlling natural phenomena.
Chaos in dynamical systems is one of such limiting concepts. These systems of differential equations are typically sensitive either to initial conditions or to the measurement of the parameters of the system (instability). Fractal attractor sets are a characteristic of chaotic systems. These observations do not mean that such systems are completely beyond understanding or predictability. More often, they are complex in a similar sense to what has been discussed above about complex mathematical objects.
In this paper we will follow mainly the work of german physicist Peter Grassberger in two papers, [GR1] and [GR2], where he addresses the problem of finding a general useful complexity measure for objects expressed as strings of numbers or binary digits. Grassberger, as others, suggests using the words randomness or information contents to the property measured by Kolmogorov's definition and reserving "complexity" for something that has to be in between plain uniformity and total randomness.
When studying natural phenomena, we are interested in certain measurable quantities that we want to predict or control. A gas filling a recipient, for instance, is composed of millions of molecules, each one of them behaving accordingly to its own parameters. The dynamical system arising from that description would have a differential equation for each one of them, perhaps some 1020 degrees of freedom. We might be interested however in observables arising from their average behavior, such as temperature, volume and pressure. A small set of equations relates these numbers and allows us to predict the behavior of the whole gas disregarding the effects of an underlying structure that we just call random and is beyond the scope of what we are trying to study.
Some systems, however, do not have this nice property. The behavior, for example, of gases in the atmosphere of the earth is difficult to predict, because the future evolution of the "interesting" variables is influenced by the lower levels. This event can be described as information flowing from irrelevant to relevant degrees of freedom of the system. Randomness arises now as an inherent property of these systems, as our relevant features are being influenced by factors that lie beyond the scope of what is observable and we describe as random factors.
A similar thing happens to chaotic systems that are sensitive to initial conditions. Here it is not the extra degrees of freedom that difficult prediction, but the precision with which the variables can be measured. As immeasurable variations on these variables will have a noticeable effect on the future behavior, randomness appears again in the form information flowing from insignificant to significant digits on the parameters of the system.
The existence of random or unobservable components in a physical phenomenon, an universal condition, does not mean that all of them are complicated, as we have seen in the previous examples. We most conclude that complexity is a subjective property. If the observer is satisfied with a simple model with sufficient accuracy, there is no complexity involved.
Complexity will have to be defined now as being not just an intrinsic characteristic of the physical world but a relationship between a system and an interested observer. Kolmogorov complexity defines a measure for an arbitrary string of bits, a complexity of a mathematical object per se. But a phenomenon will only be complex when the model that describes its behavior to a certain interested observer shows certain complex properties.
Coding the description of a system as a string of characters or binary digits is the first step that these researchers take to study complexity issues on complex systems. Either a sequence of discrete variables is observed over time, or a formal, dynamical system is translated into a hopefully equivalent symbolic coding ([GR1], page 490).
We are left with a common language, that of strings of symbols over a finite alphabet, that can be examined with available theoretical tools: Theory of computation, Shannon's information theory, Kolmogorov complexity, etc. Some lines of research (see [BCSS]) might suggest that other approaches, are based in continuous instead of discrete models, are possible.
On the rest of this discussion we will assume that such a symbolic coding is available. The observed entity is a string (x1,...,xn,...) of symbols. In general we are interested in observing measures that can be observed as complexity rates, that is, limits of the form
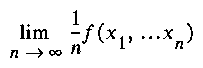 (1)
(1)
Space and time complexity of algorithms
The theory of computation has brought Computational Complexity Theory (see [H-U]). This theory classifies algorithms by their time and space requirements. A certain Turing Machine has space complexity S if for every input word of length n it scans at most S(n) cells of storage. Similarly, if a Turing machine makes at most T(n) moves for every input word of length n, T(n) is its time complexity. The time and space complexity of languages is defined by that of the Turing machines that interpret them.
Complexity is thus a measure of the rate at which an algorithm requires to consume a computational resource (time, space). The complexity of a given problem is defined as the minimum amount of resource needed to compute the solution. For a family of problems with parameter n we can observe the rate of growth of the complexity to n. A family of problems is "NP-hard" when the time required to compute the solution increases exponentially with n whereas the solution itself is growing only polinomially.
But the pure computational difficulty does not satisfy our intuitive notion of complexity. Now we will want to use the opposite argument: "Your fractal may take a long time to compute, but there's not much more there than a very simple mathematical formula".
Kolmogorov introduced this concept in the sixties [KO]. Although Cover and Thomas use the name `Kolmogorov Complexity', other authors prefer a different name. Gell-Mann [GM] calls it simply `Algorithmic Information Content' (AIC). The reason is not only that also Chaitin [CH] and Solomonoff discovered the concept independently, but the conflicting word `Complexity'. Chaitin himself seems more comfortable with `randomness' [CH2].
We have already seen that it is desirable to separate the concepts of randomness and complexity. AIC is however the most powerful concept behind all this further discussion. What researchers like Gell-Mann and Grassberger seem to be trying to do is to fix AIC to grasp a more accurate measure of complexity.
One additional problem with AIC is its uncomputability. The fact that no program can be known in advance to halt at some point makes it impossible to know the AIC of a given string.
Gell-Mann introduces the concept of crude complexity: "The length of the shortest message that will describe a system ... employing language, knowledge, and understanding that both parties share" ([GM], page 34).
This concept should retain the concept behind Kolmogorov Complexity by extracting the idea from the mathematical formulation. But perhaps its interest lies in the fact that the subjective relation between information and users that underlies the notion of complexity is immediately noticeable.
Ziv-Lempel is an algorithm to compress sequences of binary digits. It is known to be optimal in the sense that at least for ergodic, stationary processes ([C-L], Theorem 12.10.2) the compression rate obtained
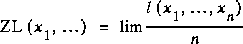 (2)
(2)
approaches the entropy rate of the source. As Ziv-Lempel does not require the set of probabilities to be known in advance, it can be used as an easily computable algorithm for calculating a complexity measure of a string.
Ziv-Lempel and AIC are not equivalent. The Kolmogorov complexity of a stochastic process can be proved to approach its entropy ([C-T], Theorem 7.3.1) but the true probabilities can never be inferred from a sequence of events. Grassberger ([GR1], p. 499) comments that for example the string of digits of ¶ is not random and its Kolmogorov complexity rate is zero. But an algorithm such as Ziv-Lempel, as well as any statistical criterion, will assign maximal entropy to the string.
This notion was introduced by C. Bennet [BE]. The logical depth of a string is defined as the complexity (as defined in theory of computation) of the shortest program that produces it.
Instead of the time taken by the fastest algorithm, as time complexity of a problem would be defined by theory of computation, first the shortest program has to be found and later its time calculated. The principle of Occam's razor ([C-T], page 161) justifies this notion: If a given sequence is found in nature, it is most likely to have been produced by the simplest program, and for practical purposes we can just assume that that is the case.
A random string of length n cannot be compressed: Its AIC will grow linearly with n, and so its logical depth approaches a finite limit as n goes to infinity. On the other hand, Grassberger points out, an apparently random string of bits generated by a cellular automata requires 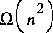 computational effort to be produced. Its AIC is constant because the program generating the automata is short, so this type of object has the property of being logically deep.
computational effort to be produced. Its AIC is constant because the program generating the automata is short, so this type of object has the property of being logically deep.
Considering time, however, leas us to, question the validity of the principle of the Occam's razor as just formulated ([C-T], page 161, [GR1], page 499).
Assuming that we observe a certain string, is it reasonable to assume that it was produced by the simplest program? If the simplest program is too slow, this is not the case. A longer program, perhaps with a tiny probability relative to the first one, but much faster, might be responsible.
As time has to be considered, let us think of a "mother nature" producing random programs as a Poisson process. Every second, either a new bit will be added to a program in preparation, or the accumulated sequence will be deployed as a new program that immediately begins running. After t seconds since the creation of the earth, the probability for a certain program of length k to appear would be about 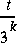 . If the program takes time T to run, the probability of that program having printed n consecutive correct output digits is
. If the program takes time T to run, the probability of that program having printed n consecutive correct output digits is
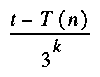 (3)
(3)
Grassberger suggests that "life emerged spontaneously, i.e. with a `program' assembled randomly which had to be very short. But it has taken some 109 years to work with this program until life has assumed its present forms." Our argument suggests that perhaps a shorter program is already running (in Mars) that will produce life pretty soon now.
Let us define the size of a computer program as the length of the instructions plus the length of the storage it uses. The size in computer memory of a running program. Given an infinite string (x1,...), for a small n the smallest program that produces the first n bits of the string will have some n digits. When n becomes large, however, the smallest program will have approximately hn+c bits, where h is the entropy of the sequence and c the "proper program length", or sophistication, as defined by Koppel and Atlan in [K-A].
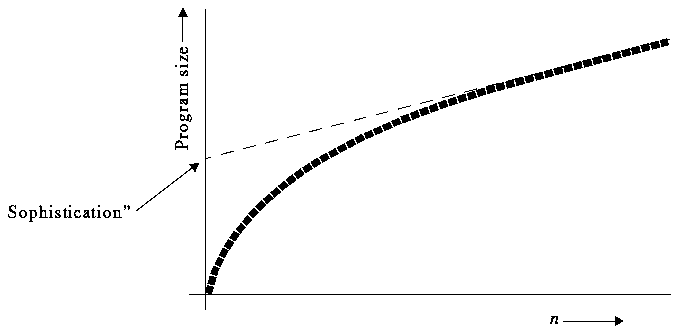
What makes this measure interesting is the fact ([GR1]) that it quantifies the importance of rules or correlations in the sequence. But he immediately points out that, for most interesting problems, the rate growth is truly hn + klogn, meaning that sophistication is infinite.
Let us now consider the sequence (x1,...) as the result of a stochastic process X=(X1,...). The sequence can be compressed up to its entropy rate ([C-T], page 63)
following the idea of logical depth, Grassberger suggests measuring the complexity (in the sense of the theory of computation) of the decompression algorithm, per symbol to be decompressed. The average amount of information about the past which has to be stored at any time in order to make an optimal forecast corresponds to this notion and is called Forecasting Complexity, FC. The name comes from the fact that an optimal decompression needs a perfect calculation of the probabilities for the next symbol, given the previous sequence ([GR1], page 505).
All this information about the past is necessary in the computation of the next symbol of the compressed string. This means that FC is a lower bound to logical depth. The shortest program will need at least FC time to compute, because it will need to explore a minimum of FC stored information.
Grassberger proposes the use of a measure of complexity as the relative memory required to calculate the probability distribution of for the next symbol of a sequence. Consider a stationary process as in the previous example.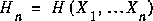 is convex, meaning that ([GR2], p. 29)
is convex, meaning that ([GR2], p. 29)
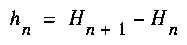 (5)
(5)
is monotonically decreasing. hn represents the additional information for a single new symbol, using the information about n previous symbols. It is clear from (3) that 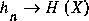 . The positive difference
. The positive difference
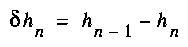 (6)
(6)
measures the amount by which the uncertainty of xn+1 decreases if x1 gets known, in addition to x2,...,xn. Grassberger's Effective measure complexity can now be defined as
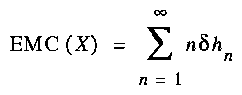 (7)
(7)
This number represents the "average usable part of the information about the past which has to be remembered at any time if one wants to be able to reconstruct the sequence X from its shortest encoding".
Its importance lies, in that it is a lower bound for the forecasting complexity, FC, as a decoding algorithm will require a storage size of at least EMC(X) bits to work out.
The use of probabilities often implies that a measure like FC will be infinite: A probability is a real number, an infinite string of digits, so infinite time is needed to calculate them. Grassberger thus favors EMC as an interesting way of assigning a formal meaning to the word complexity.
In the extreme cases, EMC behaves correctly. When the conditional entropy 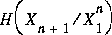 is zero for some n we have a uniform, predictable process and the EMC will be small, since
is zero for some n we have a uniform, predictable process and the EMC will be small, since 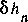 is zero. In the opposite case, when (X1,...) are iid ([C-T], page 63) we have
is zero. In the opposite case, when (X1,...) are iid ([C-T], page 63) we have 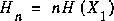 and again get
and again get 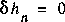 . Long-term correlations are thus the main characteristic of EMC-complex sequences.
. Long-term correlations are thus the main characteristic of EMC-complex sequences.
A main drawback of EMC is that the essential idea of Kolmogorov's complexity, that of eliminating the dependance from an external probabilistic distribution, has been resigned in order to preserve finitude in important cases and computability. Without the aid of Shannon's entropy theory, the best that Grassberger has found are the unsatisfactory concepts of logical depth and sophistication.
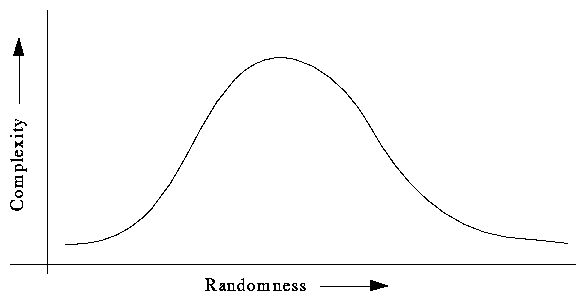
Gell-Mann's definition of Effective Complexity takes a different approach. Effective complexity is just Kolmogorov Complexity ([GM], page 56; [G-L], page 12) but measured not on an observed phenomena but through a subjective interpretation of interest to the observer, that is, a model. A model is an algorithm for specifying a probability distribution over the observed data. If the interpretation is simple, either because the phenomenon is easy to predict, or, on the other extreme, no regularities are found and it is described just as a sequence of independent random events, the complexity of the model is small. The effective complexity will be high when the AIC of the description of the probability distribution, is so. ([GM], pages 59 and 104 illustrates with graphs similar to fig. 2)
But this definition, if simple, is relative to the efficiency of the model. It is not that a better prediction is not desirable or necessary, so effective means that it is the practical complexity of the phenomenon. We will effectively carry an umbrella tomorrow just in case -because no good prediction of the probability of raining is available- but that does not mean that a better model can be found to predict the weather.
The concept of total information adds the second layer to Gell-Mann's treatment of the problem. A model filters the information and stores its regularities, but leaves its behavior as unpredictable, random, to a certain extent. The total information or augmented entropy is defined as the sum of the complexity of the model plus the (Kolmogorov) complexity -or just Shannon entropy- of the remaining irregularities ([G-L], page 13).
This concept can be used to compare the success of different models. A small model will have a large entropy, another model might reduce entropy but introduce a more complex description. A theoretical `best' model will minimize total information, representing the ideal balance between a complex description and unpredictability. Getting wet one day might be a reasonable trade-off for having the hands free on a hundred sunny days. This idea is close to the notion of sophistication, where the size of the program is added to the size of the data and an minimum is to be found.
Complexity has proved to be an elusive concept. Different researchers in different fields are bringing new philosophical and theoretical tools to deal with complex phenomena in complex systems.
Kolmogorov complexity, simultaneously discovered by three independent scientists, brought a powerful theoretical tool to compare different strings of information under a new point of view. Different independent researchers have also attempted to expand the concept to grasp a delicate intermediate point: Complexity is, should be, neither order nor chaos, but something else.
We have examined mainly the ideas of Peter Grassberger and Murray Gell-Mann. The first does a painful effort to approach a computable, satisfactory, formal notion of complexity, and gets close to his objective with the concept of Effective Measure Complexity. He is the first, however, to point out the problems: EMC is defined only on stochastic processes, and -unlike FC- is measuring an elusive "useful information" instead of the desired computational complexity. When attempts are made to improve EMC, big problems show up: Uncomputability, infinite measures that prevent comparison, etc.
On the other hand, Gell-Mann proposes a Total Information measure that is simple and extends some interesting aspects of the insights that Kolmogorov complexity has into the way we study scientific discovery and theories. Gell-Mann's concepts, however, are more philosophical, as he does not attempt to obtain methods for the estimation of the minimal total information nor to study particular cases to see if they are finite or infinite. Efforts in this direction might run into the same difficulties that Grassberger has.
Effective complexity and total information emphasize the subjective nature of complexity as a relationship between natural phenomena and an interested observer. Complexity is more in the way that phenomena are observed (i.e., the model used) than in complicate elaborations made after the model has been imposed.
Gell-Mann's theory might be better if observed under its own light: He puts the central ideas in a couple of simple concepts, leaving the rest as `random'; Grassberger reduces this randomness only slightly but pays with the introduction of notions that are difficult to understand.
Perhaps in this line we could still defend Kolmogorov complexity as the deep insight into the properties of binary strings, the simple idea with practical and philosophical consequences. But it is true that from all these incomplete theories a new resolution could arise that would be again simple, and profound.