Jim Storer


Burrs - 23
Knot Shaped Three Piece Burrs
Wood Knot - 29
Grooved Three Piece Board Burr - 30
Cross Keys (a.k.a. Three Piece Puzzle) - 31
Knotted Cube - 32
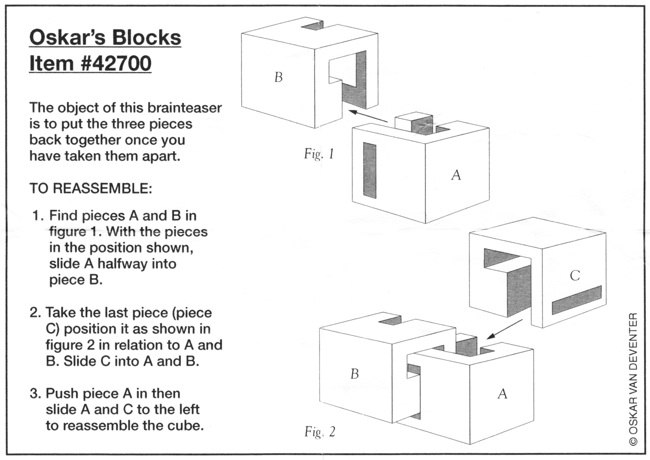
Oskar's Blocks - 33
Shaekel Knot - 34
Cheers - 35
Standard Shaped Three Piece Burrs With A Single Trick
Segerblom Knot - 36
Slideways Burr - 37
Sonneveld Three Piece Burr - 38
Triple Play - 39
Standard Shaped Three Piece Burrs
Just The Three - 40
Just 3 - 41
3 Piece Burr Yamaosa - 42
Three Open Windows - 43
GigaBurr & GigaBurr II - 44
Cubie Burr & Cubie Burr #2 - 45
Burrs With Four Pieces
JA6PB - Just Another 6-Piece Burr - 46
Accordion - 47
Burrs With Five Pieces
Disguised Burr - 48
Switch Board Burr - 49
Rift - 50
La Taupe - 51
Octo Burr - 52
Standard Six Piece Burrs
Simple 6-Piece Burr - 53
The Puzzle (a.k.a. Double Cross) - 55
Mikado Block Puzzle - 57
Yamato Block Puzzle - 59
Devil's Knot - 60
Misfit Puzzle - 61
Coffin's Improved Burr - 63
Bill's Baffling Burr - 64
L5 Notchable - 65
Computer's Choice 3-Hole - 66
Computer's Choice 4-Hole - 67
Eight Is Enough - 68
Compter's Choice 5-Hole - 70
The Piston Puzzle - 71
Computer's Choice Unique-10 - 72
L46AA Notchable - 73
Mega Six - 74
Love's Dozen - 75
139 Burr - 76
Non-Standard Six Piece Burrs
Twelve Points To Insanity - 77
Dragon Fly - 78
Butterfly - 79
Explode-A-Burr - 80
Programmer's Nightmare - 81
Holey Astigmatism - 82
NOS No. 7 - Seizaine - 83
U-Nam-It Burr - 84
Bill's Ball Bearing Burr - 85
Blind Burr - 86
Luxemburr - 87
Brass Monkey 2 - 88
Around The Bend - 89
Frantix - 90
Dovetail Burr - 91
Lock Nut - 92
Three Pieces Puzzle - 93
Tri Again - 94
Zauberflote - 95
Zig-Zag Knot - 96
Amulet - 97
Combined Burr - 98
Knotted Burr - 99
Six Piece Plate Burrs
Chen's Six Board Burr - 100
Chocolate Dip Burr - 101
Gordian Knot - 102
Bent Board Burr #2 - 103
Burrs With More Than Six Pieces
Japanese Shape Burrs (a.k.a. Kumiki Puzzles) - 104
Drueke Burrs - Bill's and Marian's Puzzles - 106
Missing Notch - 107
Uranus - 108
Gaia - 109
Elena's Burr - 110
Miyako Wooden Puzzle - 111
The Aeroplane Block Puzzle - 112
Sydney Harburr Bridge - 113
Bill's Ball Buster - 114
Hectix (a.k.a. Hexsticks, Notched Hexagonal Sticks) - 115
Locked Blocks - 117
Block Puzzle Senior - 118
Satellite Burr - 119
H Burr - 120
Sears Tower - 122
Wausau '81 - 123
Wausau '82 - 124
Wausau 83 - 125
Wausau 84 - 126
Burry Joint - 127
Lassen Risti - 128
Old Oak Of England - 129
Lattice - 130
Quadlock1 - 131
The Pacco Puzzle - 132
Q.E.D. - 133
Miyako 21-Piece - 134
Binary Burr - 135
Visible Burr - 136
SM24 Burr - 140
Multi Burrs
Fusion Burr - 149
Four Burr Stick - 150
Four Burrs - 152
Lost Day (a.k.a Eight Burrs) - 153
Berserk BurrCirc - 154
Framed Burrs
Oskar's Cube - 156
Two Piece Oddity - 157
Pair Dance - 158
Three Sticks Trapped - 159
Three Trapped Sages - 160
Pandora's Box (a.k.a. Internal Combustion) - 161
Spacemine - 164
Locked Sticks - 165
Two Halves Cage - 166
Constrained Burrs - 167
Burr Sets
Simple 6-Piece 6-Solutions Burr Set - 168
Burr Set JCC - 169
CCH Level 1 Key Piece Burr Set - 170
Interlocking Puzzles Burr Set - 172
Interlocking Puzzles Burr Set #2 - 177
Cube Assembly - 180
Pieces Made from Unit Size Cubes
Soma Cube - 181
Half Hour - 182
IP Five Piece Cube - 183
Coffin Quartet - 184
Four X - 185
Bedlam Cube - 186
Century Cube - 187
Pieces Made from Rectilinear Non-Cubic Shapes
Patio Block - 189
Patio Block MPA - 190
Splitting Headache - 192
Pieces Based on Polyhedral Dissections
Quadro Cube - 193
Diagonal Cube - 194
Slideways - 195
Apparently Impossible Cube - 196
Pieces With Interlocking Connections
Cubes And Pegs - 197
Cubes And Pegs Version B - 198
L-Bert Hall - 199
Five Minute Puzzle - 200
Corner Block - 201
Pieces Of Eight - 202
Groovy Cubes - 204
Twenty Cube - 205
Rik's Kiddy Wrapping - 206
Play2CubePart2 - 207
Liberal Cube - 208
Manipulation of Connected Cubes
Folding Cubes - 209
Hinged Cubes - 210
Kev's Cubes (a.k.a. Snake Cubes, Serpent Cubes, Cubra Cubes) - 212
Cubra Cubes - 214
Misc Cube Assemblies
Helix Cube - 215
Packing (including 2D Shapes) - 216
Checkerboard Puzzles
Checkerboard (a.k.a. All Square Novelty Puzzle, Check-A-Board, ...) - 217
Sectional Checkerboard Puzzle - 218
Chequers (a.k.a. Famous Bug House Puzzle) - 223
The Bug House Puzzle - 225
Famous Baffling Checkerboard Puzzle - 226
XceL Checkerboard Puzzle No. 1 - 227
XceL Checkerboard Puzzle No. 2 - 228
Gyro Checker Board Jig Saw Puzzle - 229
Draught Board Puzzle (a.k.a. Krazee Checkerboard Puzzle, Zebas Puzzle,...) - 230
Adams Idiot's Delight Checkerboard Puzzle - 233
Japanese 19 Piece Checkerboard Puzzle - 234
Richter Tangram and the Other 36 Anchor Stone Puzzles
Anchor Puzzle Tangram (a.k.a Caricature, Cut-Up Square ... Richter No. 8) - 235
The Nine (a.k.a. All Nine, Richter No. 1) - 245
Lightning Conductor (a.k.a. Richter No. 2) - 247
Egg Of Columbus (a.k.a. Columbus' Egg, Columbian Puzzle, Richter No. 3) - 251
Patience Prover (a.k.a. Richter No. 4) - 254
Trouble Killer (a.k.a. Richter No. 5) - 257
Heart Puzzle (a.k.a. Richter No. 6) - 261
Kobold (a.k.a. Richter No. 7) - 267
Circular Puzzle (a.k.a. Richter No. 9) - 269
Cross Puzzle (a.k.a. Richter No. 10) - 272
Not Too Hasty (a.k.a. Richter No. 11) - 276
Pythagoras (a.k.a. Richter No. 12) - 279
Tormentor (a.k.a. Richter No. 13) - 285
BeQuiet (a.k.a. Richter No. 14 /3) - 290
Sphinx (a.k.a. Lott's Stone Puzzle, Richter No. 15 / 16) - 293
Magic Egg (a.k.a. Miracle Egg, Richter Anchor Stone Puzzle No. 16 / 17) - 297
Wrath Breaker (a.k.a. Richter No. 17) - 299
Richter Anchor Stone Puzzle No. 23 - 303
Richter Anchor Stone Puzzle No. 26 - 304
Richter Anchor Stone Puzzle No. 27 - 305
Richter Anchor Stone Puzzle No. 28 - 306
Richter Anchor Stone Puzzle No. 29 - 307
Richter Anchor Stone Puzzle No. 30 - 308
Richter Anchor Stone Puzzle No. 31 - 309
Richter Anchor Stone Puzzle No. 35 - 313
Richter Anchor Stone Puzzle No. 36 - 314
Richter Summary - 315
Some Other Richter Puzzles and Games
Richter Piccolo Nr. T1 (a.k.a. Richter Picco Nr. T1) - 323
Richter Hamleys - 324
Richter Trench and Zoo Puzzles (a.k.a. Schutzengraben, Zoologischer-Garten) - 325
Richter Star Puzzle - 328
Richter Puzzle Mosaic No. 3 - 331
Richter Meteor 1 - 332
Richter Meteor 6 - 333
Other Tangram-Like Puzzles
The Classic Tangram (a.k.a. Richter Anchor Puzzle) - 334
Daddling - 335
Pythagoras - 336
Voodoo - 337
HiHo - 338
Sherlock Holmes - 339
Scrambled Egg - 341
121 Puzzles - 342
ELZZUP - 343
PIC-TUR-ETT - 348
King Tut's Puzzle - 350
HIQU - 351
Shape By Shape - 352
Other 2D Puzzles With Polygonal Shapes
Four F's (a.k.a. F Puzzle) - 353
Four Piece Square (a.k.a. Magic Square) - 354
Double Square (a.k.a Square Me, Five Block Puzzle, Madagascar Madness) - 355
Red Circle Puzzle - 358
Missing T (a.k.a. T Puzzle, Magic T, Cut-Up T, Pa's T Puzzle, etc.) - 359
What's Your Score - 362
FPuzzle (theF) - 363
H Puzzle - 364
Pie Without E - 365
Make A Square - 366
Major War Problem - 367
Other 2D Packing Puzzles
Checking In - 368
Decoy Puzzle - 369
Batee Baseball - 370
Blockade - 371
Four T Puzzle - 372
Pencil Puzzle - 373
Pearl In The Shell - 374
Czech Farms - 375
Seven - 376
Pentominoes
Pentominoes (a.k.a Polyominoes) - 377
Twin Box Pentominoes - 385
3D Box Filling
Block Head (a.k.a. Sneaky Squares, Stark Raving Cubes, Square Fit, KUBI) - 386
Three Piece Block Head (a.k.a. The Third Degree) - 387
Coffin's 271A - 388
Log Stacker - 389
Dice Packing Box - 390
Chaotic Cube - 391
Pack It In - 394
Cube Root Blocks - 395
Parcel Post - 396
Bermuda Hexagon - 397
Matching - 398
2D Matching
Rubik's Tangle 3x3 (a.k.a Rubik's Mini Tangle) - 399
Rubik's Tangle 3x3 Double Sided - 400
Rubik's Tangle 5x5 - 401
Cluzzelei - 402
Crazy Puzzles - 403
McDonald Land Guzzle - 404
Infants Hospital - The Magic Line - 406
Krazee Links (a.k.a Endless Chain) - 407
Lost Rope - 408
Drive Ya Nuts - 409
Circus Seven (a.k.a. Mind Exerciser) - 410
Circus Puzzler (a.k.a. Color Matcher) - 411
Color Match - 412
Thinkominos - 413
Match The Colors - 414
Triazzle - 415
Bee - 416
Invisible - 417
Snake Pit - 418
Frog Pond - 419
Tool Trouble - 420
Transposer 6 & Bonbons - 421
Transposer Kaboozle - 422
Tantrix Discovery - 423
Tantrix Extreme - 424
Great Gears - 426
Spectra - 427
Instant Insanity Family
Instant Insanity (a.k.a Katzenjammer, Great Tantalizer, Face-4, ...) - 429
The Grand Army Puzzle - 442
The Allies Flag Puzzle (a.k.a. The Allied Flags Puzzle) - 443
The Allies Flags Puzzle - 444
Tantalizing Ten - 445
Cuss - 446
Iribako - 447
Drives You Crazy - 448
Boer War Puzzle - 449
Other 3D Matching
Bolygok - 451
Double Disaster - 452
Mental Blocks - 453
Disney Cubes - 454
Make A Dice (a.k.a. Spots Puzzle) - 455
Twice Dice - 456
Loony Tunes Blocks - 457
Smarts Pyramid - 458
Smarts PyramidJr - 459
The Rock - 460
Einstein Cube - 461
Rubik Triamid - 462
Other 3D Shape Assembly - 463
Convex Polyhedral Shapes
Two Piece Pyramid (a.k.a. Magic Pyramid) - 464
Three Piece Tetrahedron - 465
Four Piece Pyramid, Version 1 - 466
Four Piece Pyramid, Version 2 - 467
Four Piece Tetrahedron - 468
Truncated Tetrahedron - 469
Five Piece Tetrahedron - 470
Truncated Octahedra - 471
Truncated Cubes - 472
Garnet - 473
Y-Knot - 474
More Complex Polyhedral Shapes
Three Cubes Puzzle - 475
Three Piece Block - 476
Three Boxy - 477
Three Bunnies - 478
118-X - 479
Three Pairs - 480
Augmented Four Corners - 481
Turnabout - 482
Triumph - 483
Fusion Confusion - 484
Rosebud - 485
Twelve Piece Separation - 486
Crystal Pyramid - 489
3D Jigsaw Puzzles
Four Piece Jigsaw Puzzle - 490
Four Piece Jigsaw Cube - 491
Wonder Puzzle Block - 492
3x3 Chinese Zigzag - 493
3x4 Chinese Zigzag - 494
Wonders Of The World Cube Puzzle - 495
Jigsaw Dog - 496
Misc. Shape Assembly
Oskar's Matchboxes - 497
Pin-Hole Puzzle (a.k.a Pegged Puzzle) - 498
Wood Star - 499
Saturn Ring - 500
Rubik's Snake - 501
Yin And Yang - 502
Wooden-Do-It (a.k.a. Construction Cigar, Cigar Puzzle) - 503
Gumball Keychains - 508
Hartley's Humpty Dumpty - 509
Almost Impossible Heart - 510
Rubik's Cube Etc. - 511
Rubik's Cube - The Two That Started It All
Rubik's 2x2x2 Pocket Cube - 512
Rubik's 3x3x3 Cube - 523
More Rubik's Type Cubes
Rubik1x2x2 - 539
Rubik 1x2x3 - 540
Rubik 1x2x5 - 541
Rubik 1x2x9 - 542
Rubik 1x2x13 (a.k.a. Unlucky Twist) - 543
Rubik 1x3x3 Floppy Cube - 544
Rubik1x3x3 Floppy Mirror Cube (a.k.a. Magic Floppy Cube) - 545
Rubik1x3x3 Scramble Cube - 546
Rubik 2x2x2 Bandaged - 547
Rubik 2x2x2 Double Bandaged - 548
Rubik 2x2x2 Nested (a.k.a. Rubik 2x2x2 Super Square) - 549
Rubik 2x2x2 Cubes Fused - 550
Rubik 2x2x3 Tower Cube (a.k.a. Slim Tower, Franken Tower) - 551
Rubik 2x2x4 Tower - 552
Rubik 2x2x4 Nested (a.k.a. Rubik 2x2x4 Super Square) - 553
Rubik 2x2x23 (a.k.a. Overlap Cube) - 554
Rubik 2x3x3 Domino - 555
Rubik2x3x3 Layered - 556
Rubik 2x3x4 - 557
Rubik 2x4x4 (a.k.a. WitEden 2x4x4) - 558
Rubik's Color Blocks - 559
Rubik 3x3x3 Mirror Cube (a.k.a. Mirror Block, Yong Jun Cube) - 560
Rubik3x3x3 Fisher Cube (a.k.a. Square King) - 561
Rubik 3x3x3 Void Cube (a.k.a. Holey Cube) - 562
Rubik 3x3x3 Edges Only (a.k.a. Cornerless Void Cub) - 564
Rubik 3x3x3 Fourth Dimension - 565
Rubik 3x3x3 Scotland - 566
Rubik 3x3x3 Layered - 567
Rubik's 3x3x3 Perpetual Calendar - 568
Rubik 3x3x3 Bandaged (a.k.a. Bicube) - 569
Rubik 3x3x3 Patched (a.k.a. Fused Cube) - 570
Rubik 3x3x3 Brick (a.k.a Brick Cube) - 571
Rubik 3x3x3 Latch Cube - 572
Rubik 3x3x3 Constrained (a.k.a. TomZ / Tom's Constrained Cube) - 573
Rubik 3x3x3 Treasure Box - 574
Rubik 3x3x4 - 575
Rubik 3x3x5 - 576
Rubik 3x3x5 X - 577
Rubik 3x3x5 Cross - 578
Rubik 3x3x9 - 579
Rubik 3x3x9RoadBlock - 580
Rubik 3x4x5 - 581
Rubik 4x4x4 - 582
Rubik 4x4x4 Patched - 590
Rubik 4x4x4 Brick - 591
Rubik 4x4x5 - 592
Rubik 4x4x6 (a.k.a. TomZ 4x4x6 Cuboid) - 593
Rubik 5x5x5 - 594
Rubik 6x6x6 (a.k.a. V-Cube 6x6x6) - 597
Rubik 7x7x7 (a.k.a. V-Cube 7x7x7) - 598
Large Rubik Cubes - 599
Huge Rubik Cubes - 600
Camouflage Cubes / Evil Cuboids
Camouflage Cube 3x3x3 - 601
Camouflage Cube 3x4x4 - 602
Evil Cuboid 2x3x4 - 603
Evil Cuboid 3x3x3 - 604
Evil Cuboid 3x4x5 - 605
Crazy Cubes
Crazy Cube 2x3x3 - 606
Crazy Cube 3x3x3 - 607
Crazy Cube 3x3x7 (a.k.a. WitEden Super Magic Cube) - 608
Crazy Cube 4x4x4 - 609
Crazy Cube 4x4x4 Two - 610
Other Rectangular Shapes
Mixup Cube - 611
Ghost Cube - 612
Pocket Cube - 613
Axel Cube - 614
Skewb - 615
Holey Skewb (a.k.a. Void Skewb) - 617
Pitcher Insanity Cube - 618
Golden Cube - 619
Six Spots - 620
Dino Cube (a.k.a. Dinosaur Cube) - 621
Blue Magic (a.k.a. Black Flower Cube, Star Cube, Rex Cube) - 622
Mosaic Cube - 623
Square 1 (a.k.a. Super Cubix, Cube 21) - 624
Helicopter Cube - 632
Curvy Copter - 633
Geared Shapes
Geared 1x1x4 - 634
Geared 2x2x2 (a.k.a. David Gear Cube) - 635
Geared Mixup - 636
Gear Cube - 637
Gear Barrel - 638
Gear Cube Extreme - 639
Timur Gear Skewb - 640
Gear Shift - 641
Gear Pyraminx - 642
Gear Pyraminx2 (a.k.a. Gear Mastermorphix) - 643
Gear Minx - 644
Gear Change - 645
Gear Octahedron (a.k.a. Timur Gear Corner Turning Octahedron) - 646
Gear Ball - 647
Pyrmid and Diamond Shapes
Pyraminx - 648
Master Pyraminx - 653
Pyraminx Duo - 654
Pyraminx Diamond - 655
Jing's Pyraminx (a.k.a. Rounded Halpern-Meier Pyramid) - 656
Crazy Pyraminx (a.k.a. Crazy Tetrahedron Plus) - 657
Tetraminx - 658
Professor Pyraminx - 659
Vulcano - 660
Megaminx (a.k.a. Supernova) - 661
Holey Megaminx - 662
Crazy Megaminx - 663
Kilominx (a.k.a. Flowerminx) - 664
Master Kilominx - 665
Gigaminx - 666
Teraminx - 667
Pyraminx Crystal - 668
Helicopter Dodecahedron - 669
Skewb Diamond - 670
Super Skewb Diamond (a.k.a. Diamond Octahedron) - 671
Skewb Ultimate - 672
Skewb Kite - 673
Skewb Fourteen - 674
Pyrastar - 675
Pyramorphix (a.k.a Figurenmatch, Distortion Demon Square) - 676
Starburst (a.k.a. Star of David, Sterns Puzzle) - 677
Mastermorphix (a.k.a. Master Pyramorphinx) - 678
Dinomorphix - 679
Pillow Cube (a.k.a. Cushion Cube) - 680
Enhanced Pillow Cube (a.k.a. Polish Cushion) - 681
Confused Pillow Cube - 682
Hungarian Diamond - 683
Rhombi Diamond (a.k.a. Diamond Style Puzzler) - 684
Octahedron (a.k.a. Magic Octahedron) - 686
Full Octahedron - 687
Flowered Jewel (a.k.a Jewel Puzzler, Christopher's Magic Jewel, ...) - 688
Disc Shapes
Rubik's Cheese - 689
Rubik UFO - 690
UFO Cheese - 691
Rubik Cheese Cake - 692
Puck Puzzle (a.k.a Hockey Puck Puzzle) - 693
Saturn - 694
Hungarian UFO (a.k.a. Varia Disk) - 695
Tricky Disky (a.k.a. Tricky Disk, Mind Trapper) - 696
Smart Alex (a.k.a Alpa-2-Go) - 697
Netblock UFO / Sando Ring (a.k.a. King Ring) - 698
Octo (a.k.a. Meeting Colors, Disco Puzzle) - 699
Gerdig UFO - 700
Brain Ball - 701
Ball Shapes
Rubik 2x2x2 K-Ball - 702
Rubik 3x3x3 Ball - 703
Rubik 3x3x3 Apple - 704
Master Ball (a.k.a. Duo Master, Geo Master) - 705
Skewb Puzzle Ball (a.k.a Creative Puzzle Ball) - 708
Impossiball - 710
Dogic - 711
Misc Shapes
Rubik House (a.k.a. Eight Planets Bermuda Cube) - 712
Time Machine - 713
Rubik Barrel - 714
Cuboctahedron - 715
Rainbow Cube - 716
Rainbow Nautilus - 717
Pentahedron - 718
Pentahedron 5 Layer - 719
Crazy Pentahedron - 720
Dino Star - 722
Alexander's Star - 723
Platypus - 724
Skewb Egg (a.k.a. Golden Egg, Silver Egg, etc.) - 725
Brain Twist - 726
Roundy - 727
Other 3D Manipulation - 728
Panel Puzzles
Rubik Mini Magic Panels (a.k.a Rubik Magic Junior) - 729
Rubik's Magic Panels - 734
Rubik Magic Panels Create The Cube - 742
Rubik's Master Magic Panels - 744
Rubik Magic Cross Panels - 746
Rubik Super Magic Panels - 747
Towers Of Moving Balls Or Tiles
Whip-It Towers (a.k.a. Genius Puzzle) - 749
Varikon Towers - 750
Whip-It Ball - 752
Babylon Towers - 753
Calendar Bank - 754
Thai Tower (a.k.a. Clever Toys Tower) - 755
Numbers Barrel - 756
Missing Link - 757
Reduced Missing Link - 759
Extended Missing Link - 760
Doubled Missing Link - 761
Mini Missing Link - 763
Other Puzzles With Moving Balls or Tiles
Magic Rainbow Ball - 764
Hungarian Globe (a.k.a. Equator Ball, Magic Sphere, IQ Ball) - 765
Bolaris - 767
Magic Sphere - 768
Touchdown - 769
Twister (a.k.a. Wooden Screwball, Clever Toys Natural) - 770
Atomic Chaos (a.k.a. Kaos) - 771
Entrapment - 772
Pakovalec (a.k.a. Stupid Cylinder) - 773
Ten Billion Barrel (a.k.a. Billion Barrel, Tumbler Puzzle) - 774
Russian Revolver (a.k.a. Russian UFO, Soviet UFO, Russian Flower, Festival Flower) - 775
Back Spin (a.k.a. Loophole) - 777
Sliding Piece Can Puzzle - 778
Sliding Piece Can Puzzle - 779
Brain Racker - 780
The Orb (a.k.a. Orb-It, l'ORBS) - 781
Rubik's Shells - 782
Astrolabacus - 783
Movement of Pieces by Tilting or Pushing
Varikon Box 2x2x2 - 784
Varikon Box 3x3x3 - 785
Inversion - 786
Peter's Black Hole / Vadasz Cage (a.k.a. Inside Out, Magic Jack, IQ Cube) - 788
Mad Marbles - 789
Dice Box - 790
Clark's Cube - 791
Pionir Box (a.k.a. Pionir Cube) - 792
Rubik Dice - 793
Movement of Discs and Rings
Towers Of Hanoi (a.k.a. Pyramid Piling Puzzle, Rainbow Puzzle, Brahma Puzzle) - 794
Chinese Rings (a.k.a. Cardan's Rings, Baguenaudier) - 797
Spinout - 801
Hexadecimal Puzzle - 802
WanderRings - 806
Panex - 808
Manipulation Of Positioned Balls, Levers, Buttons, Etc.
Cmetrick - 809
Cmetrick Too (Hard) - 810
Planets - 811
SaturnLD - 812
Orbik - 815
Rolling Cubes - 816
Cross Teaser - 817
Rubik's Clock - 818
Cerebral Rings Puzzler - 820
Simultaneous Maze - 821
Misc.
Wisdom Ball (a.k.a. Mind Twister) - 822
SpongeBob PuzzlePants (a.k.a. SpongeBob Cube) - 823
Flip Side - 824
Kabalabda - 825
Rubik's Rabbits (a.k.a. Rubik's Hat) - 826
Enigma - 827
Brain Puzzler - 828
Sliding Pieces and Other 2D Manipulation - 829
Square Pieces
Fifteen Puzzle (4x4 squares, 15 tiles) - 830
RO-LET (4x4 squares, 15 tiles) - 879
Unocando (4x4 squares, 15 tiles) - 880
Missionary Puzzle (4x4 squares, 16 tiles) - 881
Sixteen Puzzle (4x4 + 1 squares, 16 tiles, a.k.a. Flintstones, Escher) - 882
Moving Day (2x3 squares, 5 tiles, a.k.a. 5-Block Puzzle, Lodging House Difficulty) - 883
Eight Puzzle (2x4 squares, 7 tiles, a.k.a Super Solitaire) - 884
Nine Puzzle (3x3 squares, 8 tiles, a.k.a. Superman, Tweety, Simpsons, etc.) - 885
Mystic (3x3 squares, 7 tiles) - 890
Magic Square 3x3 (3x3 squares, 9 tiles) - 891
Great Fifty Puzzle (4x4 squares, 16 tiles, a.k.a Magic Square 4x4) - 892
Panama Canal Puzzle (2x6 squares, 11 tiles) - 893
Bull's-Eye (3x4 squares, 11 tiles, a.k.a. Bullseye, Target, Zot) - 897
Good Luck (4x3 squares, 11 tiles) - 903
Ditho (3x5 squares, 14 tiles) - 904
Twenty (3x7 squares, 20 tiles - 907
Double Trouble Puzzle (5x5 squares, 24 tiles) - 908
Twenty Seven (4x7 squares, 27 tiles) - 909
Scrabble Pocket Puzzle (4x7 squares, 27 tiles) - 911
Cornell Crossword Puzzle (4x7 squares, 28 tiles) - 912
Thirty One (4x8 squares, 31 tiles, a.k.a. Jumble, TWIDL) - 913
Frog (4x8 squares, 31 tiles) - 914
Maps (4x8 squares, 31 tiles) - 915
SKOR (4x8 squares, 31 tiles) - 916
ScribeO (4x8 tiles, 31 tiles) - 917
Octopix (4x8 squares, 31 tiles) - 918
Forty Nine (7x7 squares, 48 tiles - 919
LINGO (4x14 squares, 55 tiles) - 920
Square Pieces With Obstacles
Grandpa's Car (a.k.a. Slide-Blocked Sliding Block) - 924
Time Puzzle - 925
Work Or Golf (a.k.a. Motor Garage Puzzle, Parka Car, Sputnik, E Peg Puzzle) - 928
Honor And Glory (a.k.a. Black And White) - 931
One Fish Another Fish - 933
Russian Rows - 934
Nite and Day(s) (a.k.a. Ride or Walk) - 935
Ride or Walk (a.k.a. Nite and Days) - 936
1234 Puzzle (a.k.a. Nite and Days, Ride or Walk) - 937
Fish or Dive - 938
Work or Golf Abridged - 939
1x2 Pieces and (in most cases) 1x1 pieces
Get My Goat (a.k.a. Kapture The Kron Prinz, Boogie Man, Center Point, ...) - 940
Line Up The Quinties - 946
Johnson City Puzzle - 948
Four Suits 2 - 950
Puzzle Contrast - 951
Sliding Arrow Through The Bottle Puzzle - 952
Slidem WWII Puzzles - 953
Monarch - 957
Sliding Chess Mate 36 - 958
Straight Arrow - 959
Dad's Puzzler Family - 4x5 Trays and Multiple Shapes Rectangular Pieces
Dad's Puzzler (a.k.a. Moving Puzzle, Tit-Bits Teaser 1, Pennant Puzzle, ...) - 960
Dads Puzzler - Humdinger Version - 996
Dad's Puzzler - Exchange Version / Infants' Hospital - 1003
Quzzle And Quzzle Killer - 1010
Nine Block - 1014
Red Donkey, with Simple TJ, Century, Super Century (a.k.a. L'Ane Rouge, ...) - 1017
Traffic Jam / Let Me Through - 1027
Century Puzzles - 1032
Grand Master With Little House - 1038
Ushi And Ushi-Flipped - 1041
Hole In One With Royal Out and King Out - 1044
Fence The Cow - 1047
Dad's Puzzle Family Set With Fujiwara 15/22/25 and Super Compo - 1049
Dad's Puzzler Family With Obstacles and Non-Rectangular Pieces
D209 - 1054
Super Dries - 1055
Beyond Dad's Puzzler Family
Sunbeams Rainbow Puzzle - 1056
Infants Hospital Puzzle (a.k.a. Infants Progress Puzzle) - 1057
Trans-Atlantic (a.k.a. Ten Block Puzzle, Traffic Cop Tangle) - 1059
Happy Couple (with Ten Block and The Hughes Puzzle) - 1061
Flying Puzzle (a.k.a. Starry Puzzler, Tit-Bits Teaser No. 2, Ching Foo, ...) - 1067
Technocracy - 1077
George Washington Puzzle - 1078
Presidential Puzzle - 1081
Tit Bits Teaser No. 5 - 1083
Century Of Progress (a.k.a. South Pole Expedition) - 1088
Sliding Block Puzzle (a.k.a. Fifteen Block Puzzle, 1-2-3 Puzzle, ...) - 1090
Slide A While & Model Garage - 1095
Tokyo Parking / Rush Hour - 1100
Moota-Kun - 1104
Pink and Blue - 1106
Adam & Eve (a.k.a. Comic Scramble Game) - 1109
RunAway II - 1111
Neo Pink And Blue - 1113
Further Beyond Dad's Puzzler Family - Non-Rectangular Shapes
Ma's Puzzle (a.k.a. Spirit of '76, Wooden Puzzle, Rectangle Puzzle) - 1117
Dad's and Ma's Stumbling Blocks (a.k.a. Dad's Puzzler + Ma's Puzzle) - 1124
Mini Ma - 1125
Traffic Jam Puzzle (a.k.a. Tit-Bits Teaser No. 4) - 1126
Naoyuki Iwase 2012 - 1133
Naoyuki Iwase 2014 - 1135
Triple Tango - 1137
Clouds And Sheep - 1138
Slider (a.k.a. Hole In One) - 1139
Heart-In - 1140
Soap - 1141
Block Ten (a.k.a. Apple) - 1142
Climb 15 - 1148
Stumbling Block - 1154
I Want You - 1156
Neo Black And White - 1158
Just Six Pieces - 1163
Solo - 1164
Angel And Satan - 1165
Kuroko And Dairu - 1166
Windmill - 1167
Two Sliding Squares - 1170
Sliding Pieces Non-Standard Movement - Multiple Layers
Fence the Sheep - 1171
Two Butterflies - 1175
Moon and Star - 1176
Get My Sheep - 1183
Two Eggs - 1185
Sliding Cross - 1195
Football Match - 1204
Sliding Pieces Non-Standard Movement - Rotations and Turntables
Egg (a.k.a. Dinosaur Egg, Dragon's Egg) - 1207
Enjoy Life - 1213
Dustin Puzzle - 1222
Easy - 1225
Easy 1989 - 1227
Sliding Pieces Non-Standard Movement - Capture Movement
Sliding Eight 2 (Sliding Eight II) - 1229
Shimokita - 1231
H-Slider - 1239
My Towers of Hanoi - 1241
Sliding Three - 1248
Sliding Three Square - 1254
Neo Slide-9 - 1259
RunAway - 1261
Easy Trap - 1263
Trap - 1266
Tricky - 1275
Dog and Cat - 1283
My Dog - 1286
Two Dogs - 1288
Stacking Cups - 1291
Train Puzzle - 1294
Sliding Pieces Non-Standard Movement - Miscellaneous
African Mask - 1295
Who's The Boss - 1303
Fusion - 1309
Movement of Buttons, Balls, Numbers, etc.
New Fifteen Puzzle - 1310
Perplexity Puzzles (Perplexity, Automobile, This is Jonah, Panama Canal) - 1311
One To Ten - 1312
Good Luck Railroad Puzzle Game - 1313
Rotos - 1314
Puzzler Novice / Challenge / Avenger (a.k.a. Turnstile, Twinspin, ...) - 1315
Rotascope (a.k.a. Taquinoscope) - 1316
Rashkey - 1318
Hungarian Rings - 1319
Hungarian Rings Triple - 1320
Hungarian Rings Quad - 1321
Hungarian Olympic Rings - 1322
One Circle Two Circles - 1323
Billiards - 1324
Billiards 9-Ball - 1325
Flower - 1326
Trio - 1327
Trio 2 - 1328
Butterfly - 1329
Subway Shuffle - 1330
Movement of Tokens
Eight Peg Puzzle - 1336
TeeZ / Brain Buster - 1337
Peg Puzzle - 1338
Hopper (a.k.a. Downsize) - 1339
Mechanically Assisted Sliding Pieces
Top Spin / No. Crunch - 1341
Turnstyle (a.k.a. Tom's Turnstile) - 1342
Line Art - 1347
Colour Match - 1348
Magic Cross (a.k.a. Zauberkreuz) - 1349
Rubik's XV (a.k.a. Rubik's Fifteen) - 1350
Tsukuda's Square (a.k.a. It, 4x4 Four By Four Puzzle) - 1351
Uriblock (a.k.a. Mix Box) - 1352
Trillion - 1353
Port To Port And Triple Cross - 1355
Switch Back - 1359
SwissMad - 1360
Modern Times - 1361
Mad Triad Challenge (Twisting Tri-Side Puzzle) - 1362
Mad Triad Handy (Twisting Tri-Side Puzzle) - 1363
La Cerradura Doble - 1364
Elemental Neon - 1365
Fluorine - 1367
SF PP STAR 29 - 1368
String and Wire Puzzles - 1369
Move or Remove a Ring
Horse Shoes - 1370
Ball And Ring (a.k.a. Ball And Chain) - 1371
Moving Rings (a.k.a. Moving Beads, Tiger Cross, Wizzard Wedding Ring) - 1372
Wits End - 1373
Single Loop Wit's End - 1375
Loop Trap - 1376
Parallel Dimension - 1377
Disengage Two Pieces
Nails - 1378
Wire U's - 1379
Wire P's - 1380
Wire Heart - 1381
Cast Loop - 1382
Cast Ring - 1383
Vortex - 1384
Simple Knot 47091 - 1385
EZ Atom 47092 - 1386
Lucky Clover - 1387
Misc.
Rod and Loop - 1388
Hide The Knots - 1389
Beer Bottle Puzzle - 1390
Other Puzzles - 1391
Mechanicl Challenges
TakitaparT (a.k.a Take It Apart) - 1392
Double Puzzle - 1393
Rook Puzzle - 1394
Bolt And Ball - 1395
Spark Plug Puzzle (a.k.a. Bougie, Get Charged) - 1396
Cage Puzzle - 1397
Nut Case - 1398
Drive The USA - 1399
Screwball - 1400
Dexterity Puzzles
Abercrombie & Fitch Dexterity Puzzles - 1401
A Ward In The Infant's Hospital (a.k.a. The Little Patients Puzzle) - 1402
ElsieCow - 1403
Reiss Style 393 - 1404
Crazy Maze - 1405
Metro - 1406
Perplexus - 1407
Puzzle Boxes
Parrot Box - 1408
Spin Box - 1409
Coffin's Double Play X-48 - 1410
Stickman Grandfather Clock - 1411
Stickman Oak Wood Slide Box - 1417
Stickman Fulcrum Box - 1423
Pirate's Wallet Box (a.k.a. Stickman No. 27) - 1424
Stickman Burr Tile Box - 1433
CruciBox - 1440
Misc
Jigsaw Heart - 1442
Infants Hospital Jigsaw Puzzle - 1443
Magic Chalice - 1444
What's Your Age - 1445
The Amazing Dr. Nim - 1446
Games - 1456
Goblet - 1457
Quixo - 1460
Quarto - 1461
Othello - 1462
Nine Mens Morris (a.k.a. Mill, Muhle, Merelles / Merilles, Mulino) - 1463
Tablut - 1465
Senet - 1467
Nannon (a.k.a. Nano Backgammon) - 1471
Make Numbers - 1472
Books - 1473
Hoffmann Related Books
Hoffmann's Puzzles Old and New (1893) - 1474
Hordern's Edition Of The Hoffmann Book (1993) - 1480
Het Puzzle-Boek (1900) - 1482
Hoffmann Posthumous Books (1925) - 1483
Hoffmann's Best Math Book (2007) - 1484
Hoffmann Patience Games Book (1892) - 1485
Hoffmann's Magic Trilogy Books (1920) - 1486
Hoffmann Study Book (1977) - 1487
Other Books from Before 1960
Robert Merry's Books Of Puzzles 1-3 (1866) - 1488
Excursions Into Puzzledom (1879) - 1490
Everybody's Puzzle Book (1890) - 1491
Richter Company U.S. Brochure (early 1900's) - 1492
New Book Of 200 Puzzles (1908) - 1499
Dudeney Books (1920's) - 1500
Dudeney Posthumous Books - 1501
Sam Loyd's Cyclopedia Of Puzzles (1914) - 1502
Sam Loyd and His Puzzles (1928) - 1503
Wyatt's 1928 and 1946 Books - 1504
Johnson Smith Catalog (reprinted from 1929) - 1505
Hirschberg Book (1930) - 1506
I-X-L Puzzle Book (1938) - 1507
Filipiak Book (1942) - 1508
Everythings A Puzzle (1953) - 1509
Books 1960 - 1999
Bell's History of Board Games (1960) - 1510
Murray's History of Board Games (1978) - 1511
Delft And Botermans Book (1978) - 1512
Winning Ways Books (1982) - 1513
Hordern's Sliding Puzzle Book (1986) - 1514
Slocum and Botermans Books (1986) - 1515
Cutler's 6-Piece Burr Books (1986) - 1516
The Mathematics Of Games (1989) - 1517
Coffin's Book On Polyhedral Dissections (1990) - 1518
Coffin's Puzzle Craft Books (1992) - 1519
The Puzzle Archade (1996) - 1520
Gabarchuk's Sliding Block Puzzle Book (1996) - 1521
Frederickson's Dissections Book (1997) - 1522
G4G Tributes To Martin Gardner (1999) - 1523
Books 2000 - 2020
The Follette Puzzle Design Book (2001) - 1524
Frederickson Books (2002, 2006, 2017) - 1525
The Tangram Book (2003) - 1526
Haubrich's Checkerboard Puzzles (2005) - 1527
The Fifteen Book (2006) - 1528
A Visual History of The S.S. Adams Co. (2006) - 1529
The Self and Lensch Puzzle Design Book (2006) - 1530
Boardman's Puzzle Projects Book (2007) - 1531
The Cube Book (2009) - 1532
Hess Mathlete Book (2009) - 1533
Diaconis and Graham Book (2012) - 1534
Stickman Book (2012) - 1535
The Anchor Puzzle Book (2012) - 1537
Coffin's AP-ART Book (2014) - 1539
Books after 2020 - save a tree and go paperless!

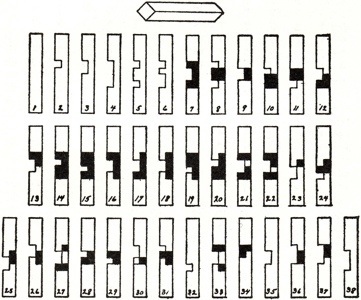
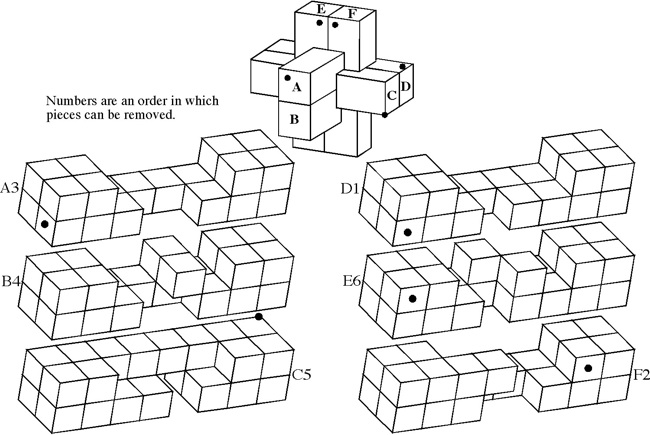
Pieces are formed by removing unit cubes from rectilinear solid pieces. A burr is notchable if it can be made with just straight cuts. Some burrs have a "key" piece that slides out. More complex ones have a number of internal voids (called holes), where removing the first piece may require sliding several pieces. An assembly of a burr is a solved shape. An assembly is a solution if it can be achieved by starting with the pieces apart and making legal moves. The level of a solution is the minimum number of moves required to remove the first piece (or separate the puzzle into two parts). The level of a burr is the lowest level of its solutions. Note that to compute level, we use Cutler's definition, where the movement of several pieces together, or the consecutive movement of pieces in the same direction, counts as a single "move". Burr level can be expressed with more than one number; e.g., 3.7.2 means 3 moves to remove the first piece, 7 moves to remove the second piece, and 2 moves to remove the third piece.
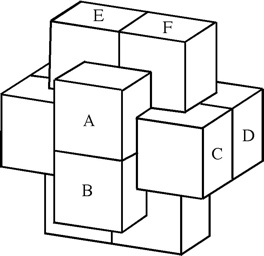
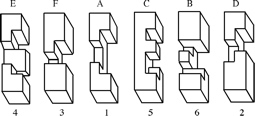
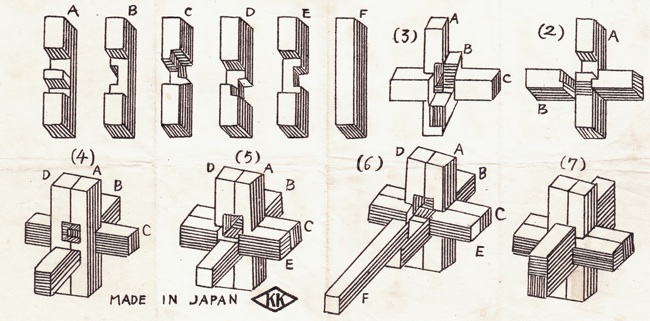
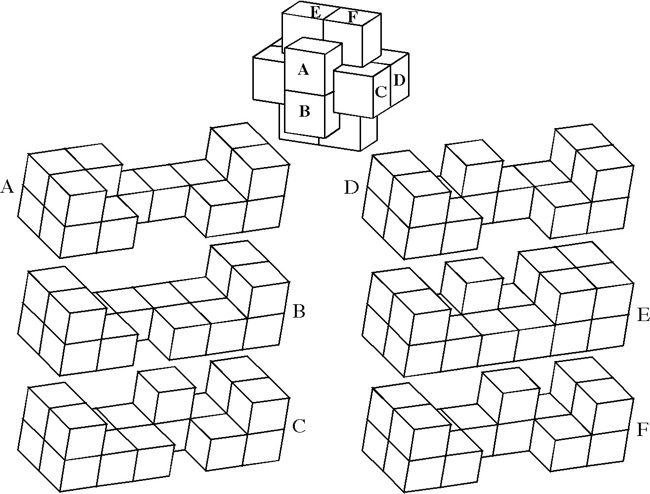
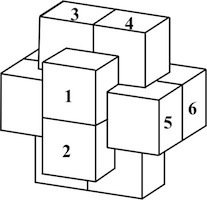
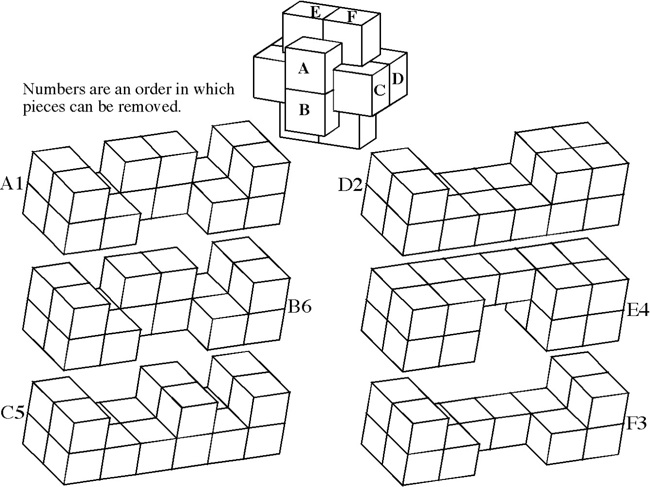
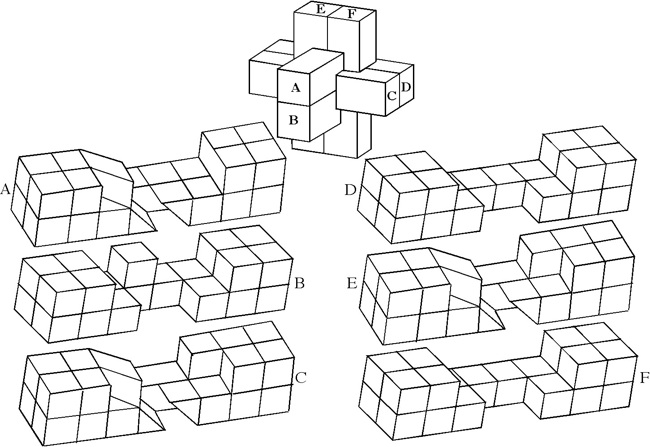
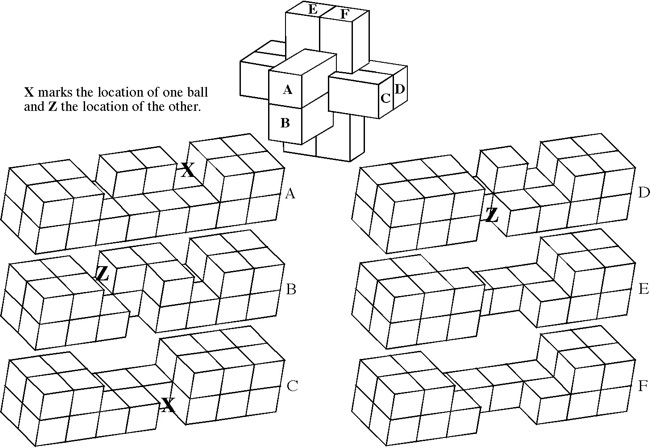
The most well known burr is the standard 6 piece burr, with 2 x 2 x 6 unit pieces (or sometimes 2 x 2 x 8). For example, the figure above shows Coffin's Improved Burr, which requires 3 moves to remove the first piece (letters show how pieces fit, numbers indicate an order in which they can be disassembled).
The number of holes in a standard 6-piece burr:Standard 6-piece burr records, from the computer work of Bill Cutler:
- Volume of six solid pieces = 6 x 24 = 144 (or 192 for 2x2x8 pieces).
- Volume of a solid burr = 24+24+16+16+12+12 = 104 (or 152 for 2x2x8 pieces).
- Volume difference = 40.
- Holes = (total number of unit cubes removed from the six pieces) - 40.
- Highest level for unique solution with 3 holes = 7.
- Highest level for unique solution with 4 holes = 8.
- Highest level for unique solution with 5 holes = 9.
- Highest level with a unique solution (uses 7 holes) = 10.
- There are no standard 6-piece burrs of level 11.
- Highest possible level (its the only one, but has non-unique solution) = 12.
- Highest level for unique notchable (has 7 holes) = 5.
- Highest level for notchable with non-unique solution = 10.
• Fractional or rotation moves.
• Non-rectangular cuts.
• Solutions with exposed holes.
• Ball bearing(s) inside that may have to move during solving.
• Additional moves to remove the second piece require more moves than the first.
Non-standard 6-piece burrs have six pieces but don't adhere to standard construction rules. Burrs in the theme of the standard 6-piece burrs but with more pieces can be difficult, especially when combined with non-standard constructions. Burrs with as few as 3 pieces can also be quite difficult (e.g., the Cuter Level 8 GigaBurr). Three piece "knots" fit together in a simple but non-obvious way. Some three piece burrs require unusual twists or diagonal motions.
The basic idea of a burr is quite old. The 1893 Hoffman book presents a wood knot as "Cross Keys" and a 6-piece burr as "The Nut". The Slocum and Botermans New Book of Puzzles, on page 52 discusses the Spears Puzzle knots manufactured in Bavaria in 1910 and marketed in England; it is also mentioned that six piece burrs appeared in Bestelmeier's 1803 Toy Catalog. The 1929 Johnson and Smith Catalog, on pages 254-255, shows a 6-piece burr, a two burr stick, and related wood puzzles. The Puzzlers' Tribute book, on page 260 cites a 6-piece burr called the Devil's Hoof and a 24-piece burr called the Large Devil's Hoof in a Catel's catalogue of 1785, and credits David Singmaster's example of a 6-piece burr in a 1733 Spanish book by Pablo Minguet E. Irol; also, on page 262 it credits the Mikado Puzzle as shown in the 1915 C. J. Felsman Catalogue:

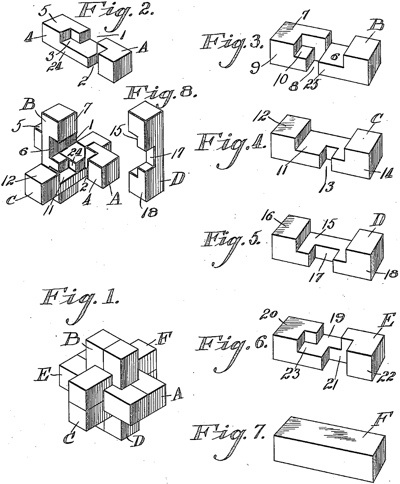
The 1942 Filipiak book has a substantial discussion of burr puzzles; here are figures it shows of a 3-piece wooden knot, a 6-piece burr, and a 6-piece burr set:
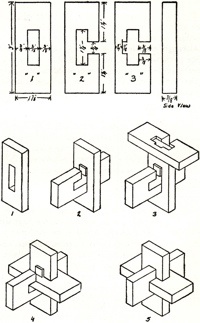
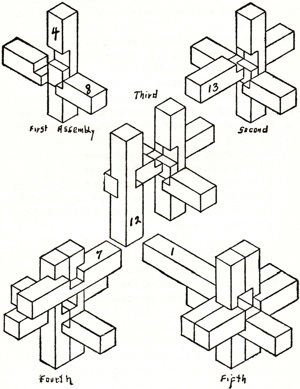
There have been many burr patents; for example, here are the figures from the 1890 Altekruse and 1917 Brown patents:
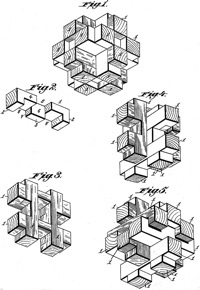
Chandler Patent, from: www.uspto.gov - patent no. 393,816
Altekruse Patent, from: www.uspto.gov - patent no. 430,502
Porter Patent, from: www.uspto.gov - patent no. 524,212
Nelson Patent, from: www.uspto.gov - patent no. 588,705
Ford Patent, from: www.uspto.gov - patent no. 779,121
Curtis Patent, from: www.uspto.gov - patent no. 781,050
Erickson Patent, from: www.uspto.gov - patent no. 985,253
Banic Patent, from: www.uspto.gov - patent no. 1,099,159
Brown Patent, from: www.uspto.gov - patent no. 1,225,760
Keiser Patent, from: www.uspto.gov - patent no. 1,261,242
Senyk Patent, from: www.uspto.gov - patent no. 1,350,039
Schenk Patent, from: www.uspto.gov - patent no. 1,455,009
Kramariuk Patent, from: www.uspto.gov - patent no. 1,542,148
Turner Patent, from: www.uspto.gov - patent no. 2,836,421
Pidgeon Patent, from: www.uspto.gov - patent no. 4,148,489
Derouin Patent, from: www.uspto.gov - patent no. 4,880,238
Dykstra Patent, from: www.uspto.gov - patent no. 5,040,797
Rob's Puzzle Page, from: http://home.comcast.net/~stegmann/interlocking.htm
Cutler's Holey 6PB Booklet, from: http://home.comcast.net/~billcutler/docs/H6PB/index.html
Cutler's Computer Analysis, from: http://home.comcast.net/~billcutler/docs/CA6PB/index.html
IBM Burr Page (edited), from: http://www.research.ibm.com/BurrPuzzles
Curfs' Page, from: http://home.tiscali.nl/~bcurfs/homepage/burrs/burrs-e.htm
Math Games Page, from: http://www.maa.org/editorial/mathgames/mathgames_08_02_04.html
Wikipedia Burr Page, from: http://en.wikipedia.org/wiki/Burr_puzzle
Mathematische Basteleien Page, from: http://www.mathematische-basteleien.de/devilsknot.htm
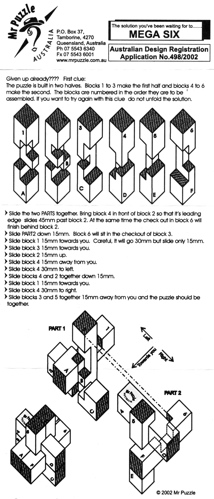
Mr. Puzzle Page, from: http://www.mrpuzzle.com.au/category129_1.htm
Source Forge Page, from: http://burrtools.sourceforge.net/gui-doc/BurrDesignTools.html

Interlocking Puzzles,
circa 2000.
(3 wood pieces, 2.75")
Daniel C. Alsmeyer 2006,
Sabriday Puzzles.
(3 wood pieces, 3")
"Triple Cross",
Puzzles & BT 2006.
(3 wood pieces, 3.2")
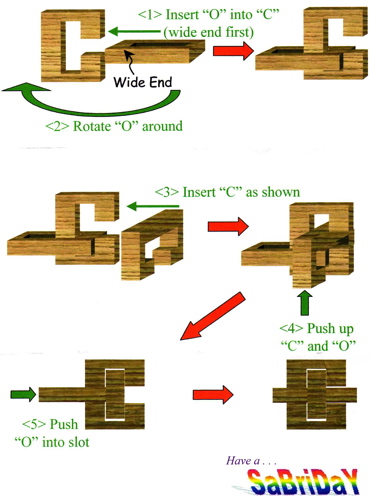
Three examples of the wood knot that was patented by M. P. Rao in 1980. Here are the directions that were sold with the Sabriday version:
Further reading:
Rao Patent, from: www.uspto.gov - patent no. 4,198,053


Designed by Kouki Kusumi, Made by Eric Fuller 2022.
(Zebrawood, Wenge, and Maple, each piece 3" x 1.75" x 1/2")
Three identical pieces make a more difficult puzzle than a traditional Wood Knot. Each piece has a groove on its long edge and a pin on the inside. The pins slide nicely in the grooves and it is natural to assume that the solved puzzle has all three pins in a groove. The key to solving is that only 2 of the three pins end up in a groove, where the third pin ends up in a piece gap.
Begin with the pieces in their solution orientation as shown in the first photo below (the left piece pin is at the bottom, the middle piece pin is at the back, and the right piece pin is at the right). Then sliding the pieces together comes naturally:







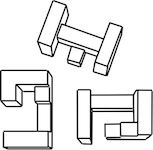
a.k.a. Three Piece Puzzle
Purchesed from Puzzles and Brain teasers Ebay Store 2006.
(three wood pieces, 3.75 inches;
described on pages 106 and 139 of the 1983 Hoffmann book)

Designed and made by Interlocking Puzzles, circa 2000.
(walnut, paduk, and hard maple, 3 inches square)
Unlike the common three piece wood knot, there are no identical pieces:


Designed by Oskar Van Deventer, purchased from Bits And Pieces, 2008.
(metal, 1.4 inches)
Here are photographs of the three pieces being disassembled:




Here is the solution sheet that was sold with the puzzle:

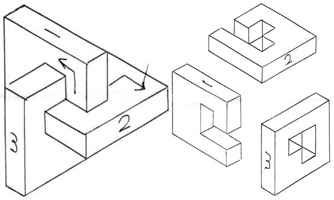
Designed by Oskar van Deventer 1983.
Made by Tom Lensch.
Sold by Cubic Dissection 2005.
(three wood pieces and solution figures, 3 inches)

Designed by Ronald Kint-Bruynseels, made by Eric Fuller 2006, Level 8.
(wood, 3 inches)
Here are the 8 assembly steps:










Designed by Wilhelm Segerblom in the late 1800's.
(three wood pieces, 2.25 inches)
The IBM Burr page cites the April 1899 issue of Scientific American as publishing this puzzle. Three identical pieces each have outer dimensions 2 by 2 by 6 units. Each has all of the center 2 by 2 by 2 portion removed except for a 1 by 1 by 2 rod that is beveled at 45 degrees (a total of 7 units of wood has been removed from each piece). To assemble, all three pieces have to be slid together simultaneously (an outside surface of the rod slides perpendicular to one piece while the beveled surface slides over the corner of another). It is not possible to put two pieces together and then slide the third one in. The figure below shows the three identical pieces in the orientation to be put together.

Further reading:
IBM Burr Page, from: http://www.research.ibm.com/BurrPuzzles/


Designed by R. Stanton, made by E. Fuller 2008.
(Curly Maple, 3 inches)
Three identical piece slide together simultaneously to make a 3-dimensional cross.
Assembly: Hold one piece vertically and determine how a second piece fits (there are only a few possibilities; look for the one where two faces sit nicely together), then carefully slide it out and put that piece down on the table without disturbing its orientation, then do the same for the third piece. Now that you have determined the orientation of the three pieces, hold them in their orientations so that they are just on the verge of engaging, line everything up, and then just squeeze the three together.
Disassembly: Randomly jiggle and push on the pieces until you can get it to come apart just a bit. You can keep doing this until the puzzle comes apart, but as it comes apart a bit you should be able to find the right way to hold on to and push two of the pieces so that the puzzle slides apart, and you can just push and pull to make it expand and contract, where the third piece is being controlled by the movement of the other two that you are holding.
Here are two views of the puzzle in a partially expanded state:



Designed by Dic Sonneveld, made by Tom Lensch, circa 1990.
(Walnut, 2.25 inches)
Three identical pieces come apart in simultaneous motion:



Designed by Jim Gooch,
made by Eric Fuller,
purchased from www.cubicdissection.com.
(three wood pieces, 2.9 inches)
At first this appears to be a three piece burr made with excess play in the fit. However, the extra play is just enough so that these three identical pieces come apart with a non-rectilinear movement.


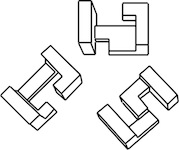
Designed by J. Krijnen, made by E. Fuller 2008, unique level 7.
(Quilted Sapelle, 3 inches)
Here are steps ito dissassemble:








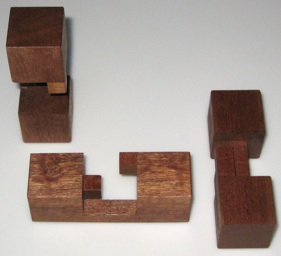


Designed by Noah Prettyman, made by Eric Fuller 2018, level 8.
(Zebrawood, 3 inches square)
The pieces are precisely made, while the puzzle overall is very loose (where in only in some positions can it be stood up without a piece sliding down). Here is what the puzzle maker said:"Just Three is from the brilliant mind of young prodigy Noah Prettyman. The level 8.4 solution is quite tricky for an interlocking burr with only three pieces. Beautifully crafted from milled zebrawood and maple, this puzzle looks great when solved! Construction is very precise, with a bit of room left for humidity expansion as it's very dry in the workshop this time of year."Here are six positions in an assembly; note that for the final photo, the left-to-right piece has been offset slightly so that it does not (by gravity) slide down a unit distance:








Designed by O. Yamamoto, made E. Fuller 2008, unique level 4 with a twist.
(Walnut, 3 inches)
Here are steps ito dissassemble (there are two photos for the second step, which is a twist):







Designed by T. Jolly, made by E. Fuller and sold by Cubic Dissection 2008, level 6.
(Bloodwood, Wenge, Holly, 3 inches)
When assembled, one can look through the center holes in any of the three directions. Here are photographs of the six steps to disassemble, where step 2 is a twist:








Designed by Bill Cutler 1999, made by Jerry McFarland, level 8.
(left: GigaBurr -Walnut, 2.2 inches; right: GigaBurr II - Cherry, 2.2 inches)
The 250 billion puzzles of this type were enumerated with a computer by Bill Cutler. The highest level (moves to remove the first piece) was 8, of which there were 80 different puzzles, where only 3 had only 9 internal voids. Two of these are the GigaBurr and GigaBurr II, and the third is a symmetric version of the GigaBurr II. To solve, two pieces can go together only one way, and then visualize the third piece in its final position to determine how to get it in and out. Here are photos of solving (the third sequence shows the symmetric GigaBurr-2 made by someone else):














Designed and made by Bill Cutler and Jerry McFarland 2001, level 6.
(left: Poplar / Walnut, 2.2 inches;
right: Cherry / Walnut / Wenge, 2.2 inches)
The basic design of the 3-piece GigaBurr and GigaBurr-2 was expanded to a 5x5x5 cube by gluing on edge and corner pieces. Cutler's computer search yielded three basic level 6 puzzles, of which these are two.

Designed by Bill Cutler.
(Walnut, 3.5 inches)
Four irregular shaped pieces and two ball bearings, which when assembled, look like a 6-piece burr. Falls apart easily.

Designed by William Hu, made by Eric Fuller, 2014.
(4 pieces, White Oak, Chakte Viga, 2" x 2" x 3")
This is what the puzzler maker says about the puzzle:"This seemingly simple puzzle uses a very interesting and difficult type of rotation. Ultra tricky and not like anything I've tried before. Level nine and fun...watch out, this one will have you pulling your hair out! Construction was tricky...the solid side spine and endgrain key pieces were fun to make, but very labor intensive. Fit is excellent; may be difficult to solve in highly humid environments due to the very close tolerances involved."At first it looks like there is no way for it to come apart. If we number the pieces 1, 2, 3, 4 going from left to right, the trick to dissassembly is to tilt piece three and rotate piece two 90 degrees (clockwise as you look through the puzzle from left to right). The puzzle generally has a nice loose fit, but it is a tight fit at the point of the rotation.









Designed by Emil Askerli, made by Eric Fuller 2016.
(5 pieces, Cherry & Walnut, 2+5/8 inches square)
In the photo above, the dark piece is not a single piece; the front portion is attached to the top right and the back portion is attached to the top left. Here is what the puzzle maker said:"I had already chosen the puzzles for the next update when Emil posted the Disguised and Camouflaged burr designs. I immediately contacted him for permission and squeezed them into the schedule because I thought the idea was so unique. Take a regular six piece burr but chop a piece or two in half and secure them. BOOM, now you have a traditional looking six piece burr puzzle that behaves very differently than usual. I used contrasting woods to give a visual hint of the unusual nature of these two. Disguised Burr has a level 7.2.2 solution. Construction of this puzzle is our usuall burr quality (outstanding!) with milled pieces and a precise yet accommodating fit."

Designed by Jim Gooch, made by Eric Fuller, level 9.
(Pau Amerillo / Wenge / Bocote, 3 inches)
The pieces consist of a "block", two identical "rods" in symmetric orientations, and two identical "plates" in symmetric orientations. Orientate the puzzle as shown on the left below (the right rod will drop down as shown if the puzzle is not too tight), exchange the plates by passing them through each other, then the right plate (which was the left plate) can be twisted (in two ways) and removed (or without twisting it can be slid out together with the right rod).



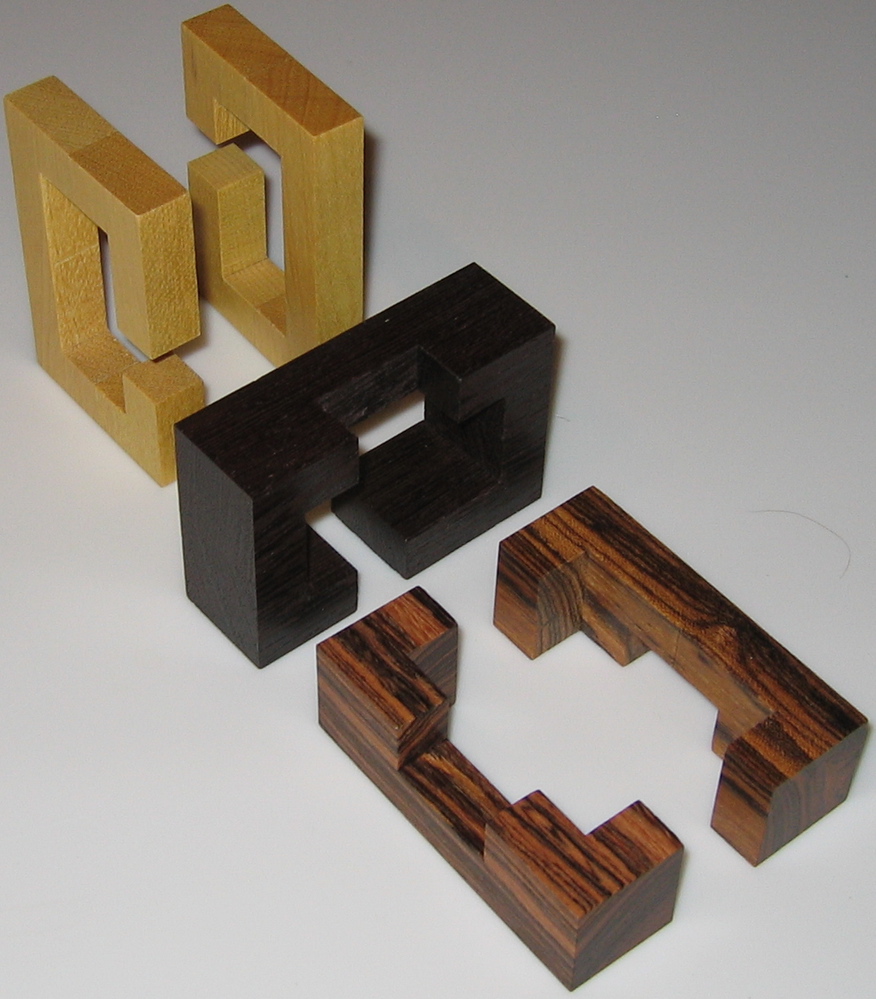

Designed by Tim Alkema, made by Eric Fuller 2017.
(5 pieces, Granadillo & Ash, 2+9/16 inches square)
Here is what the puzzle maker said:"Rift is such a simple design it's elegant. Three burr pieces and a two piece cage that dances around the assembly. The moves are so unconventional that the level 8 solution is tougher than you would expect. Disassembly has a trick to it as well. This is an excellent puzzle, I'm glad I made it, and I'm looking forward to its big brother "Schism" in the next update. Construction of this puzzle is excellent. Fit is dead on."Starting with the puzzle as pictured above, for the first four moves can be (1) the left center pushed out to the left, (2) the top center pushed up, (3) the right center pushed in to go out the back, and (4) the front top left corner of the puzzle pulled out, and then three more moves as shown below leave the puzzle apart (for a total of 8 moves after lifting the final piece off):




Designed by Alfons Eyckmans, made by Eric Fuller 2016.
(5 pieces, Wenge & Zebrawood, 2+5/8" x 2+5/8" x 1.75" inches)
Three standard burr shaped pieces fit into a box formed by the two Wenge (dark) pieces. Here is what the puzzle maker said:"La Taupe is a fairly simple puzzle with a level 9 solution but I found the shape and concept so interesting that I had to try making it. I'm glad I did, the solution is fun and more confusing than you might imagine with a mere five pieces. The contrast between the Wenge and Zebrawood is beautiful. This guy is a little gem! Construction of this puzzle is outstanding, with shouldered board construction and solid milled burr pieces. Fit is excellent."

Designed byStewart Coffin, purchased from Cubic Dissection circa 2006.
(five wood pieces, 3.5 inches)
The 5 pieces give the appearence of four sets of two. The solution is not unique.


Old design, level 1, no holes, notchable.
(six wood pieces, 3 inches)
The basic idea of level 1 with a key piece is described on pages 106 and 139-140 of the 1983 Hoffmann book. This one is even simpler. Pieces 1, 2, and 3 are identical, pieces 4 and 5 are identical, and piece 6 is a simple solid "key" piece that comes out first.
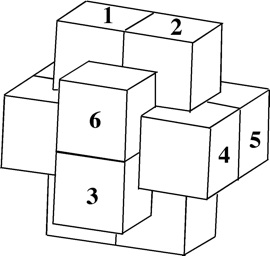
1. 2. 3. 4. 5. 6.
Assembly:1. Place pieces 1 and 2 together to form an empty rectangle shape.
2. Lay piece 3 in the bottom of the empty rectangle.
3. Place pieces 4 and 5 on either side.
4. Slide in piece 6.

Made in Indonesia 2004.
(wood, 3 inches)
Made in Indonesia 2004.
(wood, 3.2 inches)
Purchased in the 1970's.
(plastic, 2.5 inches)


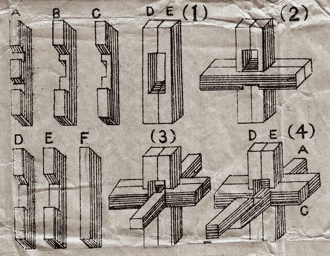
a.k.a. Double Cross
Made in Japan, circa 1930?, level 1, no holes.
(six wood pieces, each 5/16 inches square by 2.4 inches long)
Another example of a Simple 6-piece Burr. Also in the theme of pages 106 and 139-140 of the 1983 Hoffmann book, but also simpler. Two identical pieces form an empty rectangle, a double notched piece goes in the bottom, two identical pieces go on each side, and the key piece slides in:







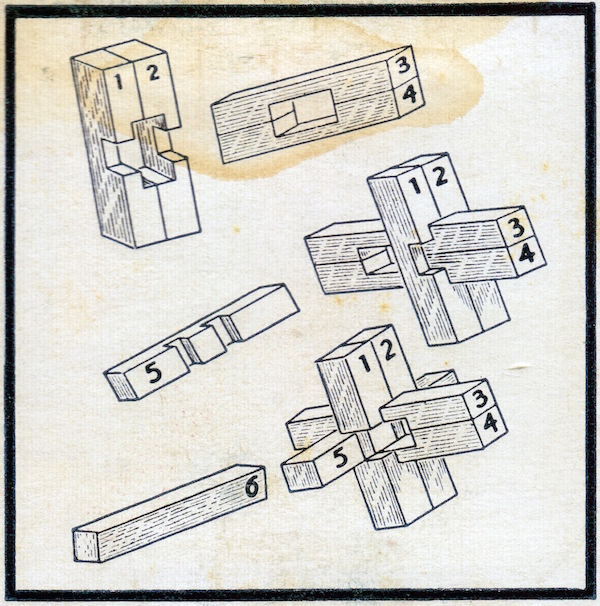



Old design, level 1, no holes, notchable., circa 1960s-1980s??
(six aluminum pieces in a cardboard box, 2+3/8" x 2+3/8" x 1/2";
directions on the back of the box are shown above)


"Made by U.N. Co. N. Y.", circa 1920?, level 1, no holes, notchable, 2x2x8 pieces.
(cardboard box, 3.2 by 2.2 by 5/8 inches, and six 1/2" x 1/2" x 2" wood pieces)
Along wth the Yamato Block Puzzle, this puzzle is discussed on page 262 of the Puzzlers' Tribute Book in a chapter by Jerry Slocum and Rik van Grol on antique Japanese export puzzles. They show a picture from the 1915 C. J. Felsman Catalog of a Mikado puzzle saying "A problem of problems ...", and note that the sililar language here, "The puzzle of puzzles ...", is further evidence that although it says NY, it may in fact be a Japanese import. Here is what is on the cover and the inside of the cover:



"Made by U.N. Co. N. Y.", circa 1920?, level 1, no holes, notchable, 2x2x8 pieces.
(cardboard box, 3.2 by 2.2 by 5/8 inches, and six 1/2" x 1/2" x 2" wood pieces)
Along wth the Mikado Block Puzzle, this puzzle is discussed on page 262 of the Puzzlers' Tribute Book in a chapter by Jerry Slocum and Rik van Grol on antique Japanese export puzzles. Here is the solution sheet that came with it and a photo of another one of these puzzles where someone has labeled the pieces:



Made in Germany, level 1, circa 1940's?
(six wood rods, 3/8" square by 2+3/8" long, with solution sheet, in cardboard box)

"Pheno-Caffein Co.,Worchester, MA, circa 1910.
(wood, 2.1 inches)
The Pheno-Caffein Co. also made the Sectional Checkerboard Puzzle, and like that puzzle, one could obtain a solution:


Designed by Stewart Coffin level 3, 3 holes.
(six wood pieces, 3.5 inches)
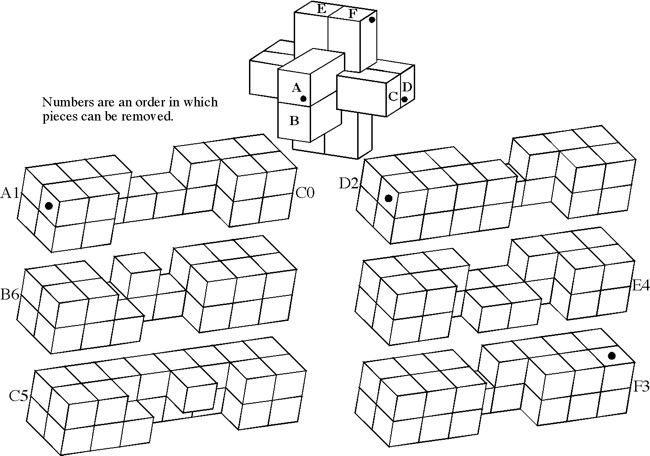

Designed and made by Bill Cutler 1984, unique level 5, 7 holes.
(Red Oak, 3 inches; 24 assemblies with a unique solution)

Discovered (by computer) and made by B. Cutler 1987, unique level 5, 7 holes.
(Mahogany, 3 inches)

Discovered (by computer) and made by B. Cutler 1988, unique level 7, 3 holes.
(Cherry, 3 inches)

Discovered (by computer) and made by B. Cutler 1988, unique level 8, 4 holes.
(Maple, 3 inches)
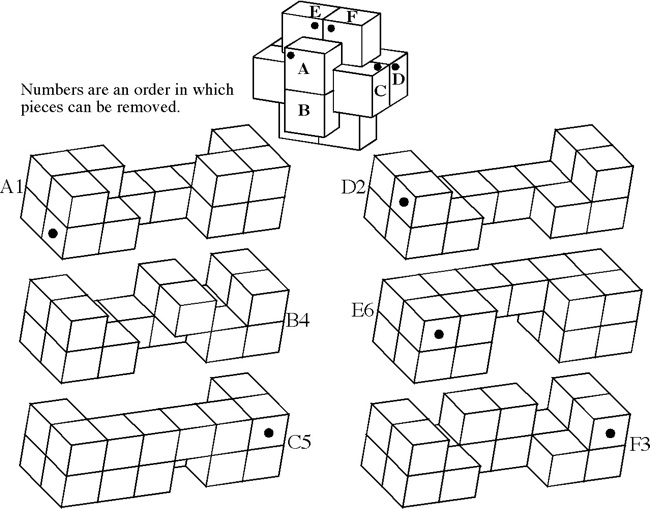

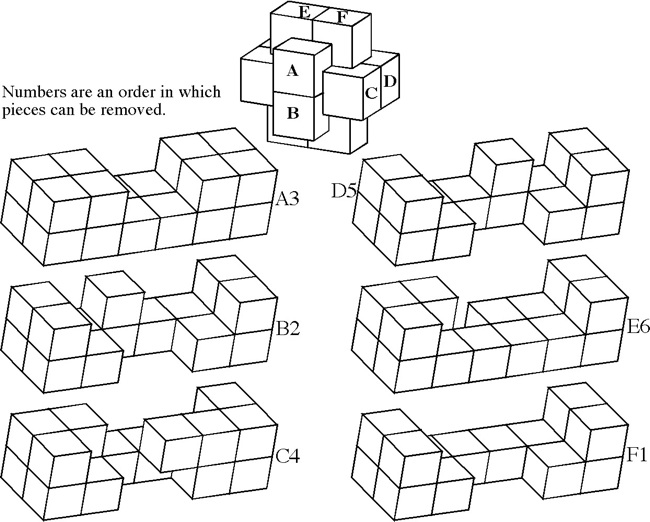
Designed by B. Cutler, made J. McFarland 2009, unique level 8, 7 holes.
(Maple / Walnut / Cherry, 2.8 inches)
Here are the first six steps:






Now the leftmost piece can be lifted up and out:


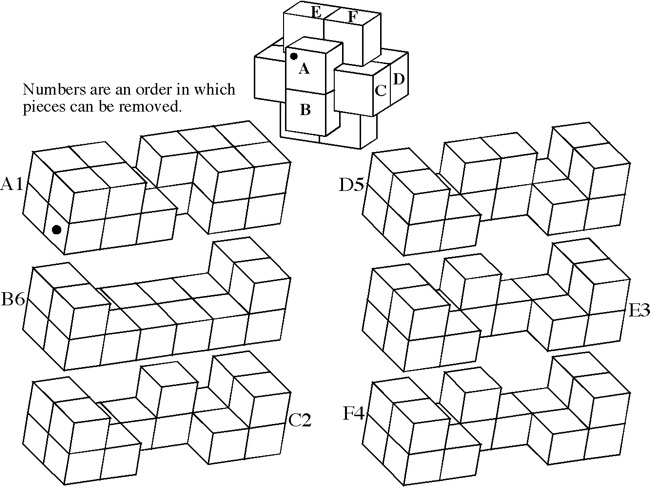
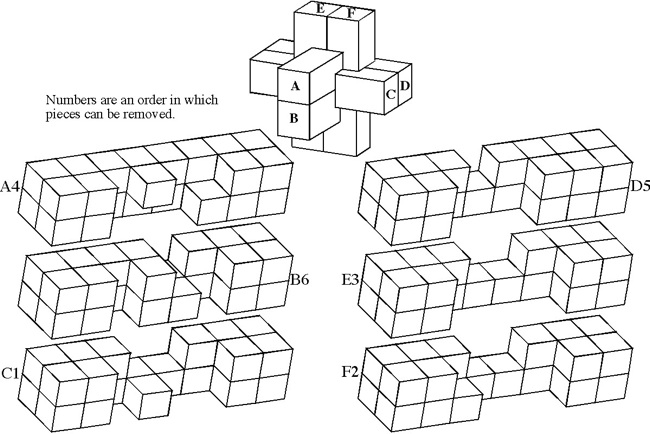
Discovered (by computer) and made by B. Cutler 1988, unique level 9, 5 holes.
(Walnut, 3.5 inches)
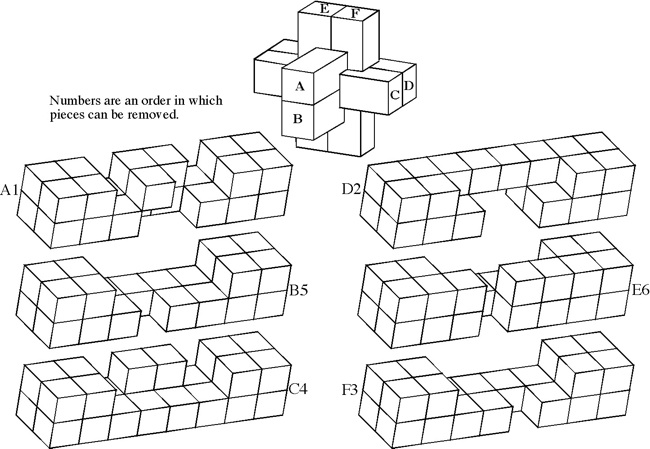

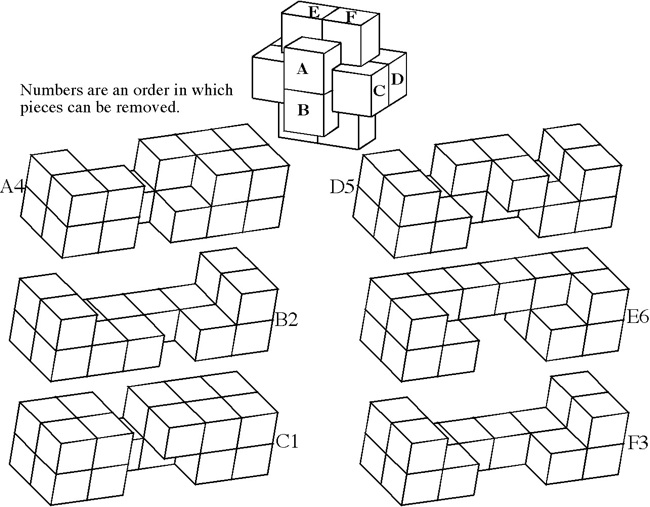
Designed by P. Marineau, made by J. McFarland 1986, unique level 9, 7 holes.
(Walnut, 3 inches)
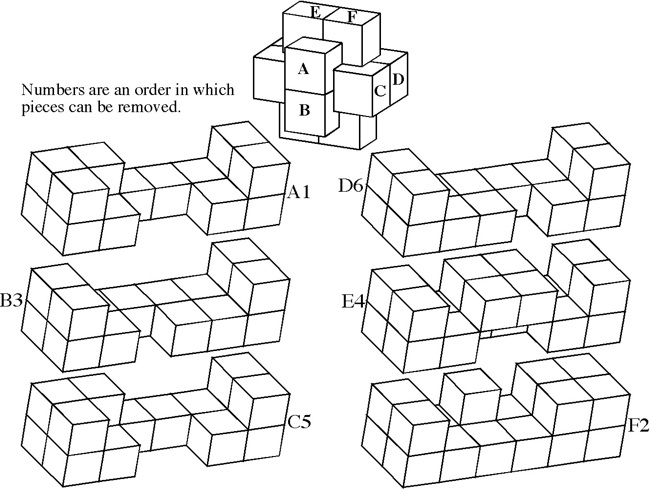

Designed by Bill Cutler 1990, unique level 10, 7 holes.
(Mahogany, 3.5 inches)
One of 18 similar unique level 10 burrs discovered by Bill Cutler with a computer program. It can be disassembled by moving (1) C /E forward 1 unit, (2) F up 2 units, (3) A back one unit, (4) D /F right 1 unit, (5) F down 2 units, (6) F forward 1 init, (7) D left 1 unit, (8) A/E back one unit, (9) B/C/F right one unit, (10) B down one unit. Note that some would consider this 11 moves since for "move" 8, both A and E can move back without dragging the other. To assemble, rather than inserting B into the pieces appropriately oriented, it may be easier to orientate things with CD facing up, and hold A/D/E (appropriately positioned) in your left hand and B/C/F (appropriately positioned) in your right hand to perform steps 10 and 9.
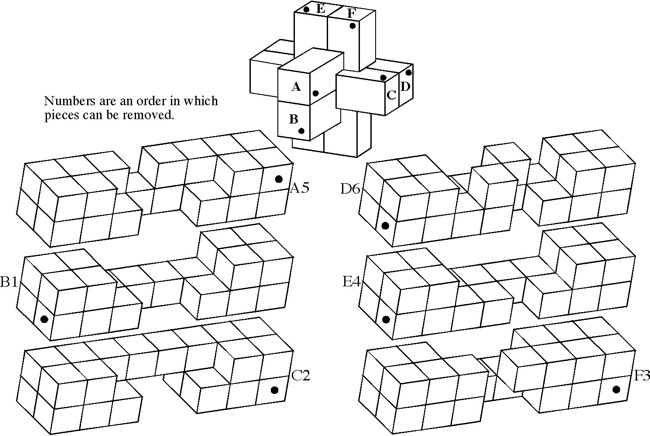

Discovered (by computer) and made by B. Cutler 1987, level 10, 9 holes, notchable.
(Maple, 3.6 inches)
Non-unique with solutions below level 10, but made to be unique level 10 by drawing diagonal lines on the pieces that must form a loop around the puzzle when solved.

Designed by Brian Young, made by Mr. Puzzle Australia, level 10, 8 holes.
(4.7 inches)
Unique Level 10 solution. One more hole than Computer's Choice Unique-10, with 20 assemblies instead of 7. Here is the solution that was sold with it:


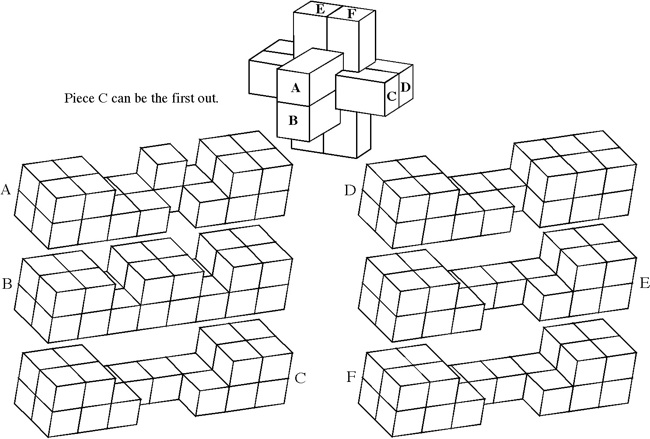
Designed by Bruce Love 1987, made by Bill Cutler, level 12, 9 holes.
(Maple, 3 inches)
According to Bruno Curfs' page, Love's dozen has 89 solutions ranging from Level 3 to one of the solutions being level 12; this puzzle made by Bill Cutler has a big D drawn on a pair of the ends that forces the level 12 solution.
Further Reading
Curfs' Page, from: http://home.tiscali.nl/~bcurfs/homepage/burrs/burrs-e.htm

Designed and made by Bill Cutler; can't be disassembled.
(Red Oak, 4.5 inches)
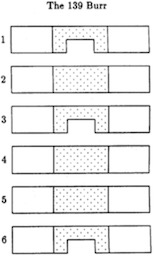
From his computer analysis, Cutler determined that 139 was the largest number of states that a standard 6 piece burr could have without having a solution, and then he chose the simplist of these for this puzzle. So this burr is made to the dimensions of a normal 6-piece burr, has lots of movement, but can't be disassembled (it was made by gluing two portions of a piece together during assembly). Here is his diagram of the pieces:

Purchased from Mr. Puzzle Australia 2006, level 1, no holes.
(six wood pieces, 3.5 inches)
Mr. Puzzle Australia credits this puzzle as being sold as early as 1875, and as having been sold under a number of names, including the Cluster, the Gem Cut Puzzle, the Chestnut Burr, and the Snowflake. When assembled it looks like a standard version of the Simple Six Piece Burr (where pieces have a diamond cross section). However, it actually is composed of six identical pieces where two assemblies of three slide together.


Made in Japan circa 1930?, level 1.
(cardboard box and 6 wood pieces, 3.75 inches;
box cover similar to other vintage Japanese exports like the Yamato Puzzle)

Made in Japan circa 1930?, level 1.
(cardboard box and 6 wood pieces, 3 inches;
box cover similar to other vintage Japanese exports like the Yamato Puzzle)
Here is the solution sheet that came with it:

Designed by Bill Cutler 1965, purchased circa 2000, level 1.
(six wood pieces, 3.5 inches)
Six identical pieces with some angled internal cuts that slide apart simultaneously.

Discovered (with a computer) and made by Bill Cutler 1989, level 5, 7 holes.
(Maple, 3.5 inches)
A programmer's nightmare because disassembly requires a twist. Move F up 1/2 unit, rotate A 90 degrees, move A up (pulling F with it by 1/2 unit), move D up, slide D out. Note that although the 1/2 move is needed theoretically, there is enough play in the puzzle that F can initially be moved up a full unit (this does not change the level since A has to be moved up in any case). This puzzle is hard for a person too, because according to Cutler's computer analysis, there are 102 assemblies (ways these pieces can exist in space in the solved shape) with only this one solution (the only way that is achievable starting with the pieces apart).

Designed and Made by Bill Cutler 1994, level 7, 4 holes, notchable.
(Cherry, 2.25 inches)
Bill Cutler credits Stewart Coffin with the idea of making burrs with slanted pieces in a way that restricts the number of possible assemblies. Cutler then found a non-unique level 7 burr from his computer analysis which became unique when made with slanted pieces. Slide F forward, slide E left (pulling D with it), slide E forward, push D right, slide F back, slide F right, remove A:


Designed by Gregory Benedetti, made by Eric Fuller 2017.
(6 pieces, Ambrosia Maple, 3 inches square)
Many angled cuts for an unusual assembly. Here is what the puzzle maker said:"With the invention of the NOS (New Old School) puzzle series, Gregory took the six piece burr format and turned it on its head. The only thing more noteworthy than the uniqueness of the series was how difficult they are to make. When he originally send me the plans, I turned him down because it just looked like a nightmare to manufacture. I changed my mind after handling a couple 3d printed prototypes. These look like traditional six piece burrs but are nothing like them. The angled internal geometry allows for some outrageous movements. They are very confusing and wonderfully different. This is the final three designs to complete the set. Construction was very challenging, requiring the creation of several new jigs and techniques. "Seizaine" is the seventh and final of the NOS designs and has the highest level. A full sixteen moves; Greg says he used "Love's Dozen" as the base but all I see is crazy angles and some woodworking challenges that were VERY difficult. Fit is very good, a little loose to account for dry conditions during the period in which it was made. This puzzle is delivered assembled."

Designed by Bill Cutler.
(Walnut, 3 inches)
Slide F back and then remove the three pieces A, C , E simultaneously by expanding them out to the upper left:

Designed by Bill Cutler1986, spin + level 3.
(Red Oak with two steel ball bearings, 3.5 inches)
Spin the puzzle in the orientation shown (around the axis defined by E and F) to position the balls, and then the two halves A,C,F and B,D,E can slide apart with three moves:


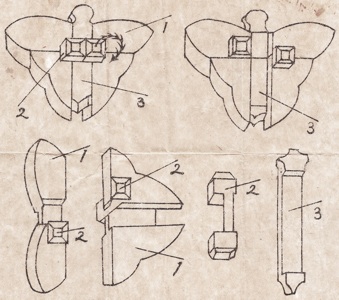
Designed by Gregory Benedetti, made by Maurice Vicourouz 2012.
(Purple Heart, 3.25 inches)
Pieces are a small cube trapped in the center, three identical "simple pieces", and three identical "complex" pieces. Assembly is relatively easy, where the three complex pieces and the cube are put compactly together as shown on the left in the figure below (rubber bands keep them together for the photo) and then the three simple pieces slide simultaneously over the exposed corner:

Disassembly requires simultaneous motion to move the three complex pieces together into the "key position" shown on the left below. One first has to identify which three are the complex pieces and then carefully jiggle and push to get all three to push in flush. In the middle is this position lit up from the back (where the serial number of the lower in-out piece can be seen), and on the right is shown the top three pieces coming apart simultaneously. The puzzle's name comes from the fact that when you don't know what is inside this puzzle, disassembly may be achieved by accident when randomly shaking and pulling on the puzzle.




Designed by Matti Linola, made by Eric Fuller 2010.
(Yellowheart and Wenge, 3 inches)
Once one sees how to solve the three piece burr formed by the light colored pieces, the dark pieces don't change the puzzle very much, but the construction and fit is terrific.
To solve:Here are photos of the assembly progressing:
- Take out the dark pieces, to first solve the 3-piece burr.
- Start with the simple U shaped piece and see that because each piece has to slide over one of the other two, there is only one way the other two can go, and then assemble the three pieces.
- Now look down each end, and it can be seen that there is only one way the dark pieces could possibly fit.
- Then take apart the three light pieces, insert the dark pieces, and push everything back together, moving the dark pieces in and out as needed.








Designed by Steve Nicholls and Ali Morris, purchases 2019.
(7 brass cylinders, where two go together to make a total of 6 cylinders, each 2.75" long)
A combination of a trick take-apart puzzle and a 6-piece burr. Looks like a 6-piece burr when assembled, but it is actually 7 pieces where half of the key piece unscrews (not a burr move). The other half of the key piece is held in by a pin so it does not fall out and is not the first piece to be removed (not a standard burr feature). Here are photos of the puzzle being assembled:








Designed by Frans de Vreugd 2005, purchased from Mr. Puzzle Australia.
level 5, 3 hole, notchable, six 2x2x6 pieces with end caps.
(Queensland Silver Ash with Queensland Blackbean ends, 3.125")
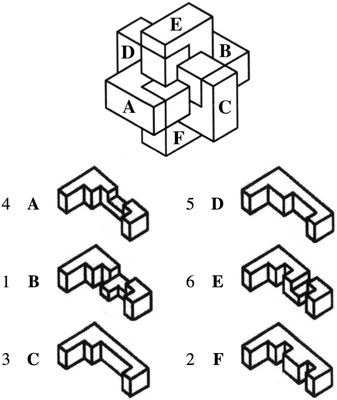
A variation of the standard 6 piece burr where end caps have been added to the pieces; highest level for this type of burr with notchable pieces. Here is a diagram of the puzzle and the pieces (numbers are the order they can be removed):



Designed by Stewart Coffin (puzzle no. 9), made and sold by Interlocking Puzzles 2000.
(wood, 6 identical pieces and 6 corresponding identical pieces, 2.6 inches)
A variation of the 1890 Altekruse burr with pins and holes for some of the notches; shown on page 79 of the Coffin Book. Below are photos of one way for inserting pieces 3 through 11; piece 12 is then added to complete the two halves as shown above, which then slide together.











Designed by Frans de Vreugd, purchased from Bits and Pieces 2007, level 6.
(wood, 3.75 inches)
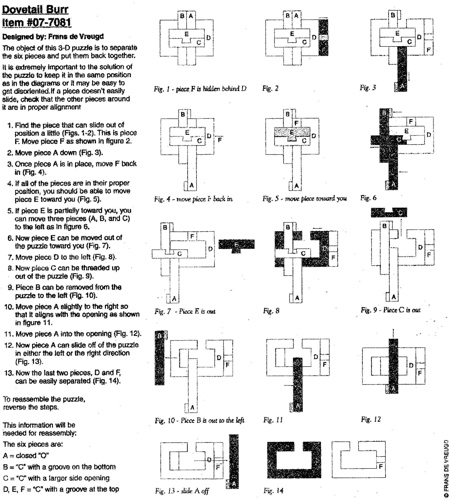


Designed by Stewart Coffin (design number 105)
Sold in 2006 by Cubic Dissection (www.cubicdissection.com)
(left Bocote / right Cocobola, both 3.25 inches)
Can be solved in two ways using the same pieces; the left above is solved using coordinate motion (all pieces moving together at the same time), and the right above is solved by halving two halves that slide together. The hardest part is trying to visualize what it should look like together once it is apart. Here is what the two solutions look like when starting to come apart:



a.k.a. Triple Play
Purchased from Bits and Pieces 2007.
(wood, 3 inches)
Looks like three pieces but is actually a level 1 non-standard 6 piece burr (six pieces (three light wood and three dark wood pieces). Here is the solution that came with the puzzle:


Designed by F. Potts, made by E. Fuller 2008, purchased from Cubic Dissection.
(Walnut and Maple, 3 inches)
Six pieces with magnetic tips assemble to look like a three piece burr (e.g., Just The Three). The pieces are all identical; here are photos of different views of them:

Here are photos of pulling apart the whole assembly and an assembly of four:


The solution is almost as much of a dexterity puzzle as a logic puzzle, where there is only one way to put two together that will lead to a solution, then it is easy to spread them apart and put in the next two, then harder to spread apart the four to get in the fifth, and then after pushing everything back together, a bit tricky with only two hands to get in the sixth piece. Here is a photo of the assembly of four with the two remaining pieces still to be put in:


Designed by Gregory Benedetti, made by Eric Fuller 2011.
(Acrylic, Yellowheart, 2.25 inches)
Here is what the puzzle maker said about this puzzle in the sale listing:"Reminiscent of Padaung Rings, this nifty little pocket puzzle is a lot of fun to solve. With a level 14.4.2 it's tricky but not impossible ... once you get the correct alignment and piece selection, it flows fairly quickly."


Copyright ThinkFun 2010.
(plastic, 2.75 inches square)
Comes with a solution booklet that has 37 steps to disassemble reading forward and 37 steps to assemble by flipping over the booklet and reading in the other direction.
Further Reading
Booklet pages.


Designed by Adin Townsend, made by Eric Fuller, 2017.
(Wenge, Canarywood, Granadillo, Maple, 4" x 4" x 2")
Here is what the puzzle maker said:"Amulet is a tricky and interesting variation on the standard six piece burr. To quote Allard's blog post about it: "He’s fiddled around with a standard six-piece burr and added a few constraining voxels around the middle and shorted one of the axes… adding those voxels makes all the difference it turns out – without them there’d be 144 solutions, with them the solution is unique… and quite tricky!" Construction of this puzzle is excellent, with a nice fit that will tolerate a fair amount of movement."



Designed by Noah Prettyman, made by Eric Fuller, 2018.
(6 pieces, Ash and Wenge, 2.24 inches square)
Two standard looking 6-piece burr pieces, two plate burr pieces, and two irregular pieces, one of which is the first to come out, as shown on the upper right above. Here is what the puzzle maker said:"Combined Burr is just a crazy puzzle that I had to make. Six pieces come together to form the familiar burr shape. Two standard stick pieces, two board pieces and two very unusual "I'm not sure what's going on here" pieces. With a whopping level 4.18 solution, this one will keep you guessing during assembly and disassembly. Crafted with Wenge and Ash, this burr is precise and well made. Shoulder joints along the length of the board burr pieces allow for the color contrast necessary without compromising strength."


Designed by Noah Prettyman, made by Eric Fuller 2017.
(6 pieces, Black Limba, 3 inches square)
Six irregular pieces form a shape like a plate burr. Here is what the puzzle maker said: Here is what the puzzle maker said:Noah Prettyman designed this wonderful new burr puzzle with the intention to recreate the standard six piece burr shape using puzzle cube type pieces. A very unique idea, and a successful one given the unique level 6.3 solution. Knotted burr is a lot of fun to solve and is quite difficult despite its reasonable seeming number of moves. I'm looking forward to whatever he comes up with next!



Designed by Chi-Ren Chen, made by Eric Fuller 2012, unique level 2.
(Walnut, Ash, American Mahogany, 3")

Designed (with a computer) by Bill Cutler and Frans de Vreugd 2001, level 13
(Hard Maple and Jatoba, 2.25 inches)
Two 1x4x6 pieces in each dimension. Making top dark wood and the bottom light wood makes the level 13 solution unique. The number of "holes" (internal voids) is 13 because the volume of assembled shape if it was solid is 104, and adding up the volume of the six pieces gives 91. Here are sheets that came with the puzzle (copyright by and courtesy of Bill Cutler).


Purchased from ThinkFun 2006.
(plastic, 6 pieces, 2.75 inches)
Made by D. Alsmeyer 2007, Sabriday Puzzles.
(6 different woods, 3.5 inches)
The booklet that comes with the retail plastic puzzle shows 65 steps to completely take the puzzle apart. McFarren's Page shows a solution that removes the first piece in 28 steps, and completely takes the puzzle apart in 35 steps.
Further reading:
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/gordian.htm
Sabriday's wood description (Mahogany, Maple, Cherry, Purpleheart, Walnut, Paduk).


Designed and made by Franz de Vreud 2003, unique level 16.
(Maple and Granadillo, 2.9 inches assembled)






These were made in Japan and owned by J. A. Storer in the 1960's. The Cleverwood Page credits these simple types of burrs to Tsunetaro Yamanaka (born 1874) and his descendants; here is a diagram of a cube from the 1942 Filipiak book, and an inexpensive circa 2000 plastic ball:

Further Reading
Cleverwood Page, from: http://www.cleverwood.com/kumiki.htm


Wm. F. Drueke & Sons, Grand Rapids, MI, circa 1940's?
(wood pieces in cardboard box, 2+5/8" x 2+5/8" x 2+5/16" high)
Examples of some classic relatively simple burrs that have been made by many over the years (e.g., see the Japanese Shape Burrs). Historical acounts indicate that Bill and Marian were Drueke family names.
Further Reading
Drueke Family History, from: www.peterspioneers.com/WRSD.htm
Drueke Directory, from: www.peterspioneers.com/WRSDdir.htm
C. Bloom Grand Rapids Press Article, from: www.peterspioneers.com/WFD.htm
Cribbage Board Article, from: http://www.cribbageboardsonline.com/article2005b.pdf

Designed by Stewart Coffin, Made by Eric Fuller 2012.
(7 pieces, Canarywood, a 13/16" cube and 6 pieces 3" long by 13/16" square)
Six burr pieces assemble with coordinated motion into a standard 6-piece burr shape with the cube trapped in the middle. t is a non-standard 6-piece burr design with the 7th cube piece added by the puzzle maker to stabilize the puzzle. I found the maniputlation of these pieces not as pleasant as I expected and gave up (for now). Here is the description quoted from the puzzle maker's page:"This puzzle was Jarry Slocum's exchange puzzle at IPP18. I was recently visiting a puzzle friend and saw it on the shelves. Spent some time working with it and finally solved it... HAD to make it. Since John Rausch did such a nice job writing up a description on his site, I think I'll plagarize from it directly:"Four of the six pieces have diagonal notches on both sides of the large, simple notch. Two pieces have them on only one side. Normally, a six-piece burr consisting only of pieces with a single, large, simple notch could not be assembled. With the diagonal notches described, it becomes a coordinate motion puzzle - a difficult one! Number 129a in Stewart's numbering system. He made 100 in 1998."I have modified the design a little bit based on Nick Baxters advice - instead of two pieces having only one notch, one piece does (leaving the other five with double notches). After some experimentation I felt that this configuration was the trickiest, and really made the solver grasp the concept behind the puzzle. Finaly, this puzzle is by nature very loose when solved. It's just a function of the notch location. I hate loose puzzles, so I included a 7th piece, which is an internal cube with magnets. This doesn't really add to the assembly, but it keeps the puzzle nicely together once solved. Happily it also makes the puzzle much more difficult to disassemble!"

Designed by Junichi Yananose, made by Eric Fuller.
(7 wood pieces, 3 inches)
Looks at first like a standard 6-piece burr. However, one of the apparent pieces is really two pieces (the one marked with a red dot in the above photo). Here is what the puzzle maker said:"At first glimpse this puzzle looks like another 6 piece burr iteration. However, disassembly will show that it holds a surprise! One of the pieces has been split, creating a very unique 7 piece burr with quite a tricky solution. Internal voids make this a level 6 burr and also create many unassemblable solutions that will frustrate the solver. This is a difficult puzzle to solve."



Designed by Yavuz Demirhan, made by Eric Fuller 2018.
(Paduak frame, 2 Wenge pieces, 2 Holly pieces, and two Acrylic pieces,
7 pieces total, 1+3/8" x 1+3/8" x 1+1/8" inches)
A tiny puzzle that came in a little pink bag. Here is what the puzzle maker said:"As soon as I saw the Gaia design I knew I wanted to make it. The structure is very unique, incorporating stick pieces and board pieces with a constraining cage. The unique level 11.2 solution is not as difficult as you would think, making this a fairly approachable puzzle. When solved the acrylic nicely sets off the three wood combination. Fit is very precise, and the cage features rabbited joinery for strength. Stick pieces are milled from solid wood."


Designed by Aleksandr Leontev, made by Eric Fuller 2016.
(8 pieces, Wenge, Zebra, Quartersawn White Oak, 2+9/16 inches square)
Looks like 12 pieces with four in each direction, but actually there are four standard burr shape pieces and four T-shaped pieces that join two rods together. Here is what the puzzle maker said:"Elena's burr is an interesting variation with a lot of tricky movement. The level 13.7 solution will keep you very very busy. Disassembly alone is a feat, with lots of dead ends. Reassembly without directions is extremely difficult. Elena's burr is an elegant design, and the ability to come up with a unique solution at such high levels with such simple pieces is an achievement. I really enjoyed making and playing with this one! Construction of this puzzle is superlative. Fit is dead-on and the pieces slide with the perfect amount of friction. I really like how this one turned out....it's possibly the best of the update."

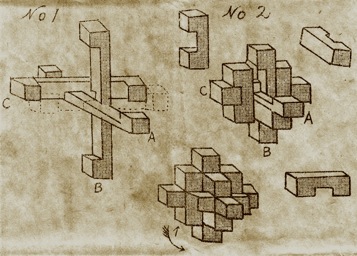
Made in Japan, circa 1930?, level 1, no holes.
(cardboard box, 2.6" x 2.1" x 7/16", 9 wood pieces, and solution sheet;
box cover similar to other vintage Japanese exports like the Yamato Puzzle;
this puzzle was also made in a 22-piece version)
Here are photos of basic solution steps:









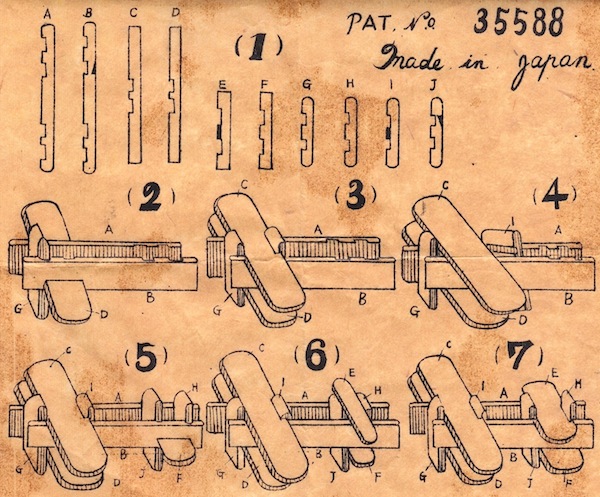
"Patent number 35588, Made In Japan", circa 1920's?
(10 wood pieces in a 3.75" x 2.4" x 1/2" cardboard box)
Easy to see how it goes together, but a bit of a dexerity puzzle to put the final piece in; two of the rectangle pieces have bevels to make that work (on on the inside middle and one on both edges).

Designed by P. McDermott, made by B. Young and P. McDermott,
purchased from Mr. Puzzle Australia in 2007, level 6.
(wood, 10 pieces, 3.25 by 6.25 by 2.5 inches)
Here are the directions and solution that were sold wih the puzzle:




Designed by Bill Cutler.
(wood, 3.5 inches, 11 pieces and 5 ball bearings)
Eleven pieces in a 2-4-5 configuration. Takes 5 balls (it came with 4 inside and you are asked to put the 5th in). Two are in a notch near the top of 11. The other three can be in a portion of the bottom part of piece 11 when it is pushed up, but in order to get 11 in place, they must be shaken out into other places that lock up the other pieces. Number the ends as follows:
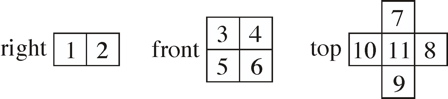
Disassembly:1. Jiggle the balls if necessary and move 11 up. 2. Two balls are always in a notch near the top of 11; jiggle the other three so that they are in a cavity at the bottom of 11. 3. Slide 8 up (1 and 2 get dragged with it). 4. The balls will now all fall out. 5. Slide 5 out. 6. Slide 11 out. 7. Slide 3 and 10 out. 8. Remove 7 and 9. 9. Remove 4. 10. Remove 6. 11. 1, 2, and 8 now come apart.Assembly:1. Assemble the puzzle without the balls by reversing the disassembly. 2. Slide 11 and 8 up (8 gets 1 and 2 dragged with it). 3. Put the two balls in the top and then slide a pencil through the puzzle to keep them from coming out. Then turn the puzzle over and put the other three balls in. 4. Slide 8 down (dragging 1 and 2 with it) as you carefully remove your pencil. 5. Shake the three balls so they leave the bottom of 11; then slide 11 down.



a.k.a. Hexsticks, Notched Hexagonal Sticks
Patented by S. Coffin 1973, made by 3M 1970,
also discovered independently by B. Cutler.
(12 plastic pieces, 3.5 inches)
Three solutions for assembling the twelve notched sticks are described on pages 116-118 of Coffin's book. The package is shown above; it has the directions on the bottom (also shown above) and inside is a hexagonal shaped solution booklet. Below are two panels from each side (other three are shown on the next page):


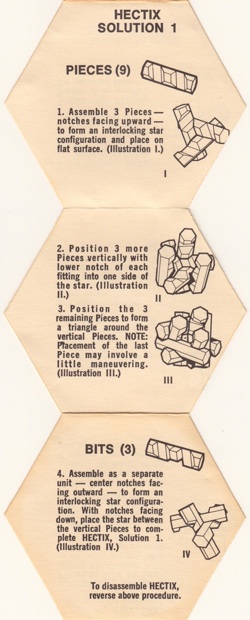
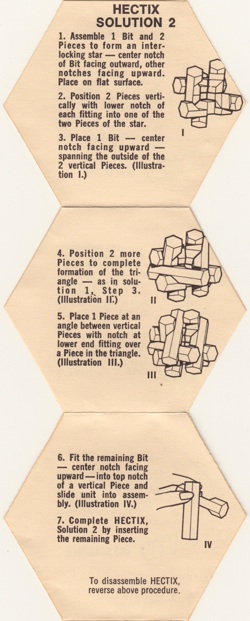
Further Reading
Coffin Patent, from: www.uspto.gov - patent no. 3,721,448
Cutler's Hectix Page, from: http://home.comcast.net/~billcutler/stock/hectix.html
Cutler's Hectix Revisited Page, from: http://home.comcast.net/~billcutler/stock/revisited.html

S.S. Adams Co., 1961.
(12 plastic pieces, each 1.5 by 3/8 by 3/8 inches)



S.S. Adams Co., 1961.
(12 plastic pieces, each 1.5 by 3/8 by 3/8 inches)


Purchased from Bits and Pieces 2007.
(10 wood pieces with solution sheet, 4.5 inches;
shown as "The Mystery" on pages 107-108, 141-142 of the 1893 Hoffmann book)

Copyright 1991-2007 Junichi Yananose, purchased in Japan 2010.
(aluminum, 12 pieces, 3.5 inches square)
Here is the box and the text on the front and back:



The puzzle slides apart in two halves and a free piece:


Designed by Bill Cutler and made by Jerry McFarland 2003.
(Walnut, 12 pieces, 2 by 2 by 8 inches)
Here is the sheet that came with the puzzle (copyright by and courtesy of Bill Cutler):

Designed by Bill Cutler 1981.
(Maple / Walnut / Cherry, 3.7 inches, 12 pieces)

Designed by Bill Cutler 1982.
(Maple / Walnut / Cherry, 4 inches, 13 pieces)


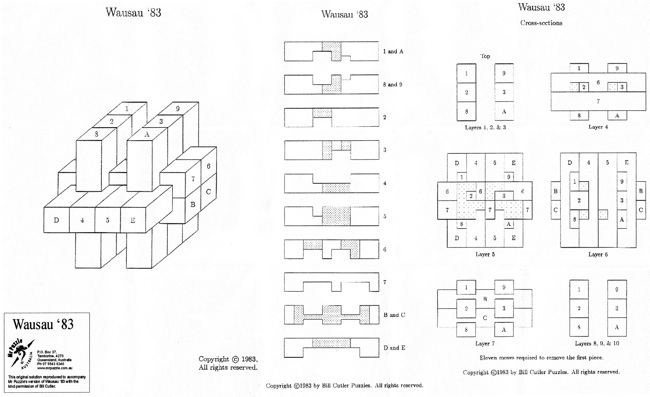
Designed by B. Cutler in 1983, made by Mr. Puzzle Australia 2008, level 11.
(Queensland Silver Ash / Queensland Blackbean / Mackay Cedar, 14 pieces, 4";
sold with directions and solution shown above)

Designed by B. Cutler 1984, made by E. Fuller 2008.
(Maple / Walnut / Mahogany, 15 pieces, 4 inches)

Designed by Bill Cutler and made by Jerry McFarland 2000.
(wood, 3 inches, 13 pieces + 2 pins)
Looks like the Wausau '82 puzzle, but different inside; here are excerpts from the puzzle sheet (copyright by and courtesy of Bill Cutler):
- Position the puzzle on a table so the group of three are vertical and the group of six with the dot is facing you, with the dot on the right (upsidedown from the figure).
- Give the puzzle a hard spin clockwise to move the pins into their holes.
- Simultaneously, the center rod of the three goes up, the rod with the dot comes out toward you, and the rod to its left goes back away from you. You will see the pins in the ends of the rod with the dot and the one next to it (take them out so you don't lose them).
- Now the puzzle comes apart.

Designer unknown, made by Eric Fuller.
(Purpleheart / Maple / Lacewood, 13 pieces, 2.25 by 3 by 3.75 inches)
Here is what Eric Fuller says:"This 13 piece interlocking burr puzzle was published in the magazine Soumen Kuvalehti number 11 in 1926. There are 2 possible solutions, both very similar. Despite its not being a high level puzzle, the solution is surprisingly tricky, probably because of its unusual shape. Ishino Keiichiro posted it on his site and Matti Linkola discovered the magazine."


Level 1, circa early 1900's??
(4" wood box with directions and 18 wood pieces, 3.6 inches assembled;
right vertical piece in photo above is solid key piece.)

Designed by Bill Cutler 1975.
(Maple / Walnut / Cherry, 3.6 inches, 18 pieces)

Designed 1992 and made by Jerry McFarland, purchased from cubicdissection.com 2008.
(Walnut, Mahogany, Maple, 19 pieces, 3.5" by 2.6" high, 7/8 inch square sticks)
Disassembly involves manipulating the central 4 pieces like opening a lock.
Here is the diagram of the pieces from the solution sold with the puzzle and photos of removing three pieces:


Further Reading
Solution that was sold with the puzzle.

"Made in Japan K.K.", circa 1920's?
(20 wood pieces, 4 inches;
box cover similar to other vintage Japanese exports like the Yamato Puzzle)
Two pairs of identical 4" pieces, four identical 2.5" pieces, eight identical 1.3" pieces, and four identical 1.3 inch solid pieces assemble to a somewhat two-dimensional snowfake arrangement; here is a photo of the box and the solution sheet:



Purchased from Pentangle Puzzles 2007.
(wood, 7.5 inches, 20 pieces)
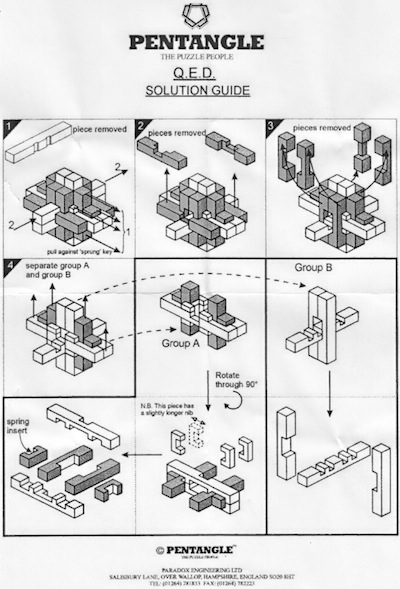

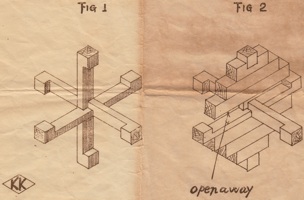
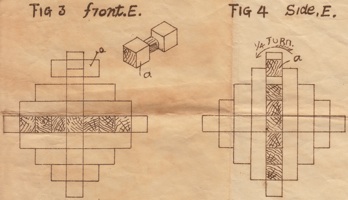
Made in Japan, circa 1930?, level 1, no holes.
(cardboard box, 4.1" x 3.4" x 1/2", 21 wood pieces, and solution sheet;
this puzzle was also made in a 9-Piece Version)

Designed by Bill Cutler and made by Jerry McFarland 2003, level 85.
(Cherry / Walnut, 21 Pieces, 3 by 3 by 3.6 inches)
The Binary Burr functions like the Chinese Rings puzzle:

There are six "ring" pieces that must be manipulated in order to remove the "bar" piece; the remaining 14 pieces don't move and form the "cage' that constrains the movements. It basically takes two moves for each move of the corresponding Chinese Rings puzzle.

Designed by Bill Cutler 1978, made by J. McFarland 2012.
(24 Maple, Walnut, and Cherry 3/4" rods, 5.25" square assembled)

Designed by Bill Cutler 1978, made by J. McFarland 2012.
(24 Maple, Walnut, and Cherry3/4" rods, 4+3/8" square assembled)

PDesigned by L. Kleinwaks, made by Eric Fuller 2013.
(Walnut, Cherry, Maple, 2.25" x 2.25" x 4")

Purchased from Interlocking Puzzles 2000.
(wood, 2.5 by 2.5 by 9.8 inches)
Four standard 6-piece burrs that share one dimension. Pieces 4, 8, and 10 are identical, pieces 1, 5, and 15 are identical, pieces 12 and 16 are identical, pieces 11 and 14 are identical, and pieces 9 and 13 are identical:
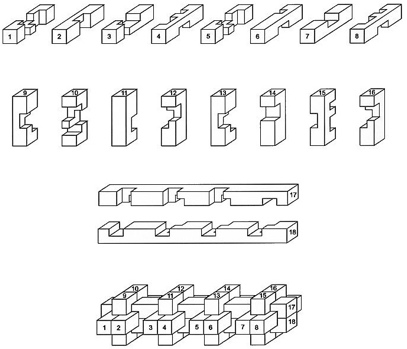

Designed by Wayne Daniel 1982, made by Interlocking Puzzles.
(wood, 4.8 inches)
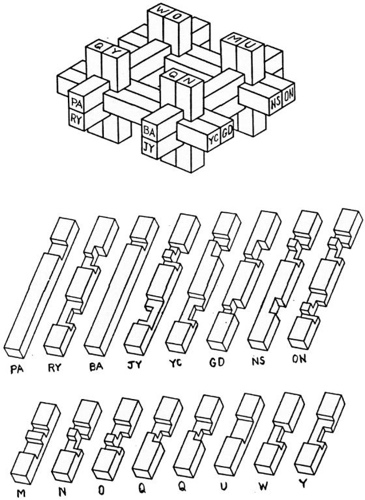

a.k.a. Eight Burrs
Designed by David Bruce, made by Interlocking Puzzles 2000.
(wood, 24 pieces, 4.8 inches)
The basic idea is to combine two eight piece assemblies and then add eight "outer" pieces. Here are diagrams of the pieces from the solution that came with the puzzle:
Assembly A pieces:
Assembly B pieces:
Outer pieces pieces:

Further Reading
Lost Day solution that was sold with the puzzle (pdf 9 pages).

Purchased from Interlocking puzzles 2002.
(13 ply Baltic Birch rings 7.2", Australian Jarrah rods 2.25", 18 pieces)
Four 6-piece burrs connected in one dimension by a pair of rings. Requires multiple counter rotations of the rings to disassemble or assemble. Interlocking Puzzles said:
"The eight radial pieces have slightly angled notches and can be sorted into four right handed and four left handed pieces. The eight axial pieces have normal notches. The four unique higher level burrs are distinctly different. The lengths of the burr rods are greater than 6 units. If these were four stand alone burrs they would require five, four, or three moves to get the first piece out. One of them would also require three moves to get the second piece out. It is a fun challenge to assemble each individual burr onto the rings and then remove it before facing the larger challenge of the whole puzzle."


Purchased circa 2000.
(plastic, 2.25 inch cube with 3D cross)
Similar idea to the Two Piece Oddity, with a frame and a 3D cross like piece that has to be removed.

Designed by Tom Jolly, made by Eric Fuller circa 2000.
(T'Zalam, 3 inches)
A frame and a 3D cross like piece that has to be removed.

Designed by Osanori Yamamoto, made by E. Fuller 2013, Level 14.
(Jatoba and Purpleheart, 2.25" x 1.5" x 1.8")
To disassemble, exchange the two trapped pieces, maneuver a bit, and then the two can be manipulated out of the cage; here are some selected positions:






Designed by Stephane Chromine, made by Eric Fuller, 2011.
(Walnut and Yellowheart, 3" x 2.25" x 1.5")
The top two pieces are identical. Different assemblies are possible depending on how the top two pieces are rotated. In their easiest positions, the bottom piece can be removed in 8 moves. However, in one configuration, 12 moves are required to remove the bottom piece (given a reasonable way of counting rotations). Below are 9 of the positions for disassembly starting with the top piece rotated as the puzzle was shipped. Although the middle piece starts in its correct rotation for the final steps of disassembly, after pulling out and tilting down the bottom piece, the middle piece is rotated and drops down to allow the top piece to be rotated, and then the middle piece can be pushed up and rotated back so that the top two pieces are together and up to allow the bottom piece to be removed. Note that it now takes only 8 steps to put the puzzle back together by leaving the top two pieces in their existing rotations.











Designed by Ramos & Abad, made by Pelikan 2006, level 13.
(wood, 2.4 inches)



a.k.a. Internal Combustion
Designed by Tado Muroi early 1990's.
(left: "Pandora's Box", Mr. Puzzle Australia, Queensland Blackbean, 3.5x3.5x2.25";
right: "Internal Combustion", Bits and Pieces, Aluminum, 2.25" x 2.25" x 1.5";
described in Boardman's book)
Four burr pieces (two of which are identical) in a frame. Below is a 9-step assembly (6 steps to remove the first piece) based on the piece orientations shown on the right above (except in the photo above the left two have been flipped upside-down for better viewing):
1.2.
2.

4.5.
6.

7.8.
9.

A 12-step assembly where the piece labeled 3 is reversed from the 9-step assembly shown on the preceding page:

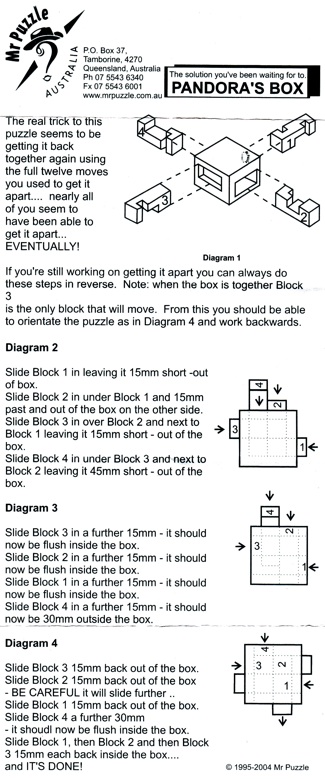
A 15-step assembly (see also the Boardman book):
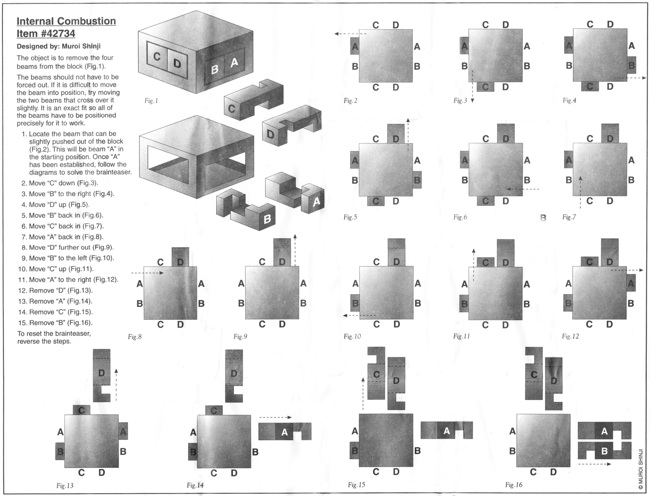










Designed by Yavuz Demirhan, made by Eric Fuller 2013.
(Sapele and Imbuya, 2.25" square, level 4)

Purchased from Bits And Pieces, 2008.
(wood, 3.4 inches square assembled by 7/8 inches thick, with solution sheet)

Designed by Gregory Benedetti, made by Eric Fuller 2012.
(Sapele and Wenge, two halves of the cage and 6 pieces, 2+5/8" square)



Designed by Logan Kleinwaks, made by Eric Fuller 2013.
(right, "Bookend Burr", Holly, Walnut, Ash, 2.5"x2.25"x2.75", level 10;
(middle, "Clamped Burr", Holly, Walnut, Ash, 2.25"x 3"x2.6", level 15;
right, "Cornered Burr", Walnut, Cherry, Ash, 2+5/8" square, level 14)
Beautifully made with high levels for rectlinear moves solutions. Shorter solutions may be possible with non-rectilear moves. For example, to remove a piece from the Cornered Burr with just three moves and some additional twisting, start by sliding the top piece to the right (if it looks like on the left below, re-orient the puzzle so it looks like the right photo below), then slide the front piece left, then up, and now, although it is easier by first sliding the bottom piece to the right, it can be twisted out without any further movement of other pieces.







Sold by Interlocking puzzles 2000.
(wood, 2.5 inches)
The only set of 6 notchable pieces that can be assembled into 6 different level 1, no-hole, standard six piece burrs. Here is the solution that was sold with the puzzle:



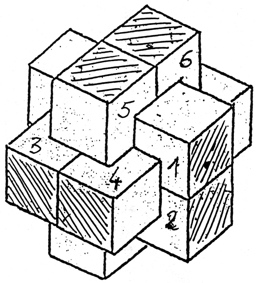
Designed and made by Jean-Claude Constantin, purchased used 2006.
(13 pieces, set is 6.25" x 3.25 x 2.5 inches, each piece is 3/4 x 3/4 x 3 inches)
A set of 13 pieces to make 40 different notchable 6 pice burrs; the same set of 6 is sometimes used for several different problems (pieces in different positions). Each piece is 2 by 2 by 8 units.
JCC's 40 Problems:
1. ADFIKL
2. ADFIKL
3. ABDKLM
4. ABDKLM
5. ABDKLM
6. ACDKLM
7. ACDKLM
8. ACDKLM09. ADGHKL
10. ADEJKL
11. AFGIKL
12. AFIJKL
13. AEGIKM
14. AFHJLM
15. ADHIKM
16. ADEFLM17. ACGKLM
18. ACGKLM
19. ACJKLM
20. ACJKLM
21. ABGKLM
22. ABGKLM
23. ABJKLM
24. ABJKLM25. ADEIKM
26. ADEIKM
27. ADFHLM
28. ADFHLM
29. AGHIKM
30. AGHIKM
31. AEFJLM
32. AEFJLM33. BCFIKL
34. BCFIKL
35. BEFHIM
36. BEFHIM
37. BEFHIM
38. BEFHIM
39. BEFHIM
40. BEFHIM
JCC's Solution Hints:
1. AK-LI-FD
2. AL-KF-DI
3. AM-IK-BD
4. AL-MK-BD
5. AK-ML-DB
6. AD-MC-KL
7. AD-KC-ML
8. AD-LC-KM09. AL-KH-GD
10. AK-LE-DJ
11. AK-GF-LI
12. AL-JI-FK
13. AK-GE-MI
14. AL-JH-FM
15. AD-IH-KM
16. AD-FE-ML17. AL-KC-GM
18. AM-KC-GL
19. AK-LC-MJ
20. AM-LC-KJ
21. AK-MG-BL
22. AK-LG-BM
23. AL-MJ-KB
24. AL-KJ-MB25. AK-ME-DI
26. AM-KE-DI
27. AL-MH-FD
28. AM-LH-FD
29. AM-IH-KG
30. AK-IH-MG
31. AM-FE-JM
32. AL-FE-JL33. BI-LC-FK
34. FB-CK-LI
35. BE-HF-MI
36. BH-EI-FM
37. FH-EM-BI
38. EI-MH-FB
39. EH-FM-BI
40. EH-MI-FB

Purchased from Creative Craft House 2007.
(wood box 3.4" x 9.25" x 4.1" with 27 wood pieces, each 3.1" long by 3/4" square)
This set has 27 2x2x6 unit standard 6-piece burr pieces numbered from 0 to 26, where piece 0 is the solid piece. A total of 69 different level 1 standard 6-piece burrs can be selected, where all use piece 0 as a key piece, and the other 5 pieces are specified with a tic-tac-toe notation:
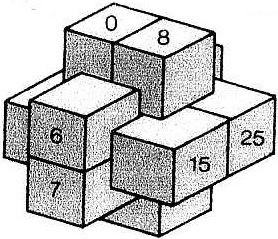


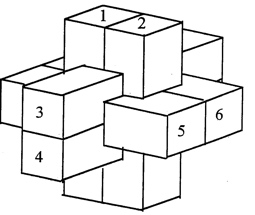
Made by Interlocking Puzzles 2000.
(7 x 6 x 3.4 inch Jarrah box with 42 Chechen pieces, each 3/4 x 3/4 x 2.4 inches)
25 distinct notchable 2 x 2 x 6.5 unit pieces, indexed from A to Y, a total of 42 pieces including duplicates, which can be used to assemble the 314 different level 1 six piece burrs that have no holes. The set comes with five puzzle cards and five solution clue cards that list the pieces in order from 1 to 6 according to where they belong in the diagram above. This set does not contain all possible notchable pieces; just has the pieces necessary (and enough copies) to make all 6-piece notchable burrs with no holes. Also, some higher level burrs can be constructed with this set; for example, L5 Notchable is OODXNL and Holey Astigmatism is TYLLUM. Note that because the pieces are more than 6 units long, there are some higher level burrs that don't quite work, but would if the pieces were exactly 6 units long.
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Puzzle number 305 is {D,G,N,O,P,Q}. The solution hint 305 lists the order {O, Q, P, D, G, N). Looking at the burr figure we can make the correspondence:With this correspondence, one can see from the figure where each piece goes in the solved puzzle (but not which way to flip or rotate it), and this can make it a fun, but still not too easy, to solve the puzzle. The trick for this one is to first see how the pieces must fit together when solved, and then realize that the only way to put it together is to put three together into one half, three together in the other half, and then slide the three halves together:
1 = O
2 = Q3 = P
4 = D5 = G
6 = N





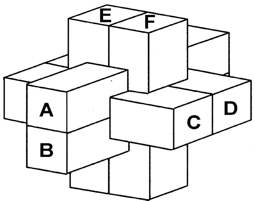
Made by Interlocking Puzzles 2000.
(6.6 x 5.75 x 3.2 inch wood box with 42 wood pieces, each 3/4 x 3/4 x 2.25 inches)
35 distinct notchable 2 x 2 x 6 unit pieces, indexed with numbers in the range 0 to 56 (as shown above), a total of 42 pieces including duplicates, which can be used to assemble most of the level 5 standard 6-piece burrs. Uses David Winkler's numbering. Four puzzle and clue cards that list the pieces in order from A to F according to the diagram above.
00
01
02
03
04
05
06
07
08
09
10
19
20
21
22
23
24
25
26
28
29
30
32
33
34
35
38
39
40
44
45
46
49
53
56

Assembling a cube shape from pieces is so common it merits its own category. Most of these puzzles leave you with a bag of pieces when unassembled, but a few, such as Hinged Cubes and Kev's Cubes are manipulation puzzles where you can pick it up, play with it, and put it down unsolved to continue later.

Copyright 1966 Piet Hein,
produced in Denmark by Skj0de of Skjern for Parker brothers, No. 1050.
(4" box with wood pieces, metal base, and instruction booklet, 3.1" assembled)
Six of the 7 pieces are formed from 4 unit size cubes and the last piece isformed from 3 unit size cubes; the goal is to assemble them into a 3x3x3 cube. This is a relatively easy puzzle with many solutions. John Rausch credits the invention of this puzzle to Piet Hein in 1936.
Further reading:
Stewart Coffin's book, from: http://www.johnrausch.com/PuzzlingWorld/chap03a.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/soma/soma.htm
Lagoon Solution, from: http://www.give-me-a-clue.com
Johnson 1988 Patent, from: www.uspto.gov - patent no. 4,784,392
Johnson 1989 Patent, from: www.uspto.gov - patent no. 4,844,466


Designed by Stuart Coffin circa 1975, made by Cubic Dissection 2002.
(6 pieces, bocote, 2.25 inches square assembled)
Here is what Coffin says in The Puzzling World of Polyhedral Dissections:
"The six-piece version of the 3 x 3 x 3 cube will be considered first. For aesthetic reasons, one might prefer that all the pieces be the same size, but this is impossible, so the nearest approximation is to use three four-block pieces and three five-block pieces. It is also desirable that all pieces be non-symmetrical but this is likewise impossible so two of the four-block pieces will have an axis of symmetry. All pieces will of course be dissimilar. Of the several thousand such combinations possible the author tried several that proved to have either multiple solutions or no solution, until finally finding one with a unique solution."
Here is the solution hint that was sold with the puzzle:



Designed and made by Interlocking Puzzles circa 2001.
(5 pieces, 3 inches square assembled)
A similar theme, but not the same set of pieces as the 5 piece version of the 3x3x3 cube suggested by Stewart Coffin in Figure 55 of The Puzzling World of Polyhedral Dissections.


Designed by Stuart Coffin (circa 1975), Made by Interlocking Puzzles (circa 2001)
(4 pieces, 3 inches square assembled)
The photo on the right above shows the four pieces in their relative orientation for assembly. Here is what Coffin says in The Puzzling World of Polyhedral Dissections:
"With puzzles of this type, there are an optimum number of pieces; and as you tinker with them, you soon gain an intuitive sense of what that number is. There is no way that a four-piece version can be very difficult, although the one shown in Fig. 51 does have the intriguing property of being serially interlocking, meaning that it can be assembled in one order only. Is a five-piece serially interlocking version possible?"


Made by AussieStuff Puzzles, purchased from Mr. Puzzle Australia, 2006.
(13 pieces, wood, 6 inches)
Thirteen pieces, each designed from unit cubes, are assembled into a 4x4x4 cube; can also be assembled into a 4 x 16 rectangle. Here is the solution that was sold with the puzzle:

Purchased from UK3, 2006.
Here is a photo of the other three sides:


Purchased from Creative Craft House 2007.
(wood, 3.1 inches)
Named because the designer's wife commented that it would take a century to solve; here are the first few steps of dissassembly:






Designed by Stewart Coffin circa 1975, made by Interlocking Puzzles 2001.
(8 pieces, maple and bloodwood, 2 inches square assembled)
The wood used to make this puzzle gives a clue to the solution with symmetric color shown above; the photos below show three basic steps to this solution:



It is not unique, here are two views of another solution:


Stewart Coffin, in his book The Puzzling World of Polyhedral Dissections, describes the derivation of this puzzle as starting with all possible pairs of joined 1x2x2 blocks (where the resulting 10 pieces can be assembled into a 4x4x5 solid in 25 different ways) and then eliminate the two rectangular pieces (the 1x2x4 piece and the 2x2x2 piece) to see if the remaining 8 pieces can be assembled into a cube. He then goes on to say that they cannot be so assembled, but that one can be eliminated and one duplicated to make a set that can. He also notes "an interesting pattern of symmetry" in the solution.
The 1986 patent of Guenther describes puzzles where pieces are formed from pairs of rectangular solids.
Further reading:
Guenther Patent, from: www.uspto.gov - patent no. 4,534,563


"Just a Little Packing Problem #1",
made by Mr. Puzzle Australia, purchased 2006;
basic idea by Stewart Coffin circa 1975.
(8 pieces, Tasmanian Oak, 2 inches square assembled)
Like the Stewart Coffin Patio Block, puzzle, but with a slightly different set of pieces. The three photos below show basic solution steps:





Designed by Bill Cutler 1991, made by Cutler / McFarland / Peterson.
(wood, 2.5 inches)
Pieces formed from black and white unit cubes and half unit cubes (starred above) must be assembled to a 3x3x3 cube with a checkerboard pattern on all sides. The solution is unique and does not follow the checkerboard pattern in the hidden center.

Designed by V. Genel, sold by Puzzleman.com, circa 2000?
(Zebrawood and Walnut, 2+5/8 inches)
Four beautifully cut pieces come apart in pairs:



Designed by S. Coffin 1971, made by T. Lensch 2008.
(Marblewood and Brazilian Blackwood, 2.2 inches;
sold with a piece diagram piece diagram and an assembly diagram)
Described in Coffin's book, six identical pieces are augmented to make 6 different non-symmetric pieces, where two groups of three slide together diagonally:




Designed by Lee Krasnow, Pacific Puzzle Works, published August 29, 2018.
(Printed on a Monoprice Mini V1 3D printer, from Thingiverse thing 2975065, 2019,
PLA plastic, 1+7/8" square)
Three identical pieces slide together in a simultaneous symmetric motion to form a cube. Below on the left shows the other three faces of the assembled cube and on the right the pieces.


Further Reading
Slideways Thingiverse Page, from: http://www.thingiverse.com/thing:2975065
Slideways Metal, from: http://www.etsy.com/listing/617915791/slideways-cube?ref=shop_home_active_16


Design and Copyright by Hirokazu Iwasawa, 2003.
Left: 3D print design by Richard Gain, thingiverse no. 23279, 2012, 1.5" square.
Right: Crafted from walnut by Alex Storer, 2022, 2+5/8" square.
The puzzle can be assembled with a simultaneous motion in two dimensions on the surface of a table. Observe that there are two identical pieces and two identical mirror images of them. Arrange one of the pairs back to back. Then, holding the the other pair back to back and upside down, place them perpendicular to the other pair. The slide all four together together with a symmetric simultaneous motion.
Here are the steps of assembling a printed plastic puzzle listed as simply "Apparently Impossible Cube" at https://www.thingiverse.com/thing:23279; this one fabricated on a Monoprice V2 printer in 2021, PLA plastic, scale 120%, infill 22%, resolution 0.175mm:




Here are the steps of assembling the walnut puzzle (made by constructing a jig for making table saw cuts with a flat top blade):






Basic idea by Stewart Coffin, made by J. Storer 1989.
(purple heart with light wood dowels, 3 inches)
Stewart Coffin proposed this class of puzzle to make a 2x2x2 cube from 8 unit cubes, where each has three mutually perpendicular holes, and a total of 12 dowels are inserted into 12 of the 24 holes. He observed that the holes have one of two "reflexive forms", and that puzzles could be made by having all pieces of one form or having 4 with one and 4 with the other. The cubes of this puzzle all have the left form; the photos show basic solution steps:







Basic idea by Stewart Coffin, made by J. Storer 1989.
(top: purple heart with dowels, 3 inches;
bottom: rosewood with dowels, 2.25 inches)
Like the Cubes and Pegs puzzle, except here 4 pieces have one form and 4 the other (the pattern of pegs in the soluton to this puzzle is different from Coffin's Book Fig. 193):




Designed by Ronald Kint-Bruynseels, made by Eric Fuller 2007.
(walnut box and 9 cocobolo pieces with pegs, 2.5 inches)
Nine identical 3-unit L-shaped pieces with pegs added to assemble in a unique solution to a 3x3x3 cube. Here are basic solution steps:





Patented by Andy Turner, made by Eric Fuller 2010.
(Oak box 2.75" square by 2.1" high, Bubinga puzzle 2.2" square)
Don't read any further; have some fun first. This puzzle is quite hard until one sees the trick, and then it is almost impossible to forget how to solve it.
The two 1x2 pieces have double holes at one end that naturally entices one to use them, but in fact these two faces butt against each other in the unique solution (no pegs going between them), and then the puzzle solves easily. Here are four photos in sequence of assembly:






Designed Stewart Coffin, made byInterlocking Puzzles 2000.
(7 pieces, bloodwood and aluminum, 3 inches)
There are a total of 7 pieces; 2 pieces formed from 5 unit cubes with holes and rods, 4 pieces formed from 4 unit cubes with holes and rods, and one 3 unit long rod. They must be assembled into a 3x3x3 cube (there is a unit void in the center). Stewart Coffin proposed this class of puzzles and suggested this particular selection of pieces as one that has a "satisfactory" set of two solutions. Below are two stages of a solution for which the last piece placed before the rod is the T, and two stages of a solution for which the last piece placed before the rod is the Z:






Designed Stewart Coffin; left Interlocking Puzzles 2005, right Coffin circa 1980.
(left: mahogany, eight pieces, 3.25 inches,
right: mahogany, walnut, szjo, eight pieces, 2.75 inches;
right is one of 6 puzzles purchased during a visit with the designer in the early 1980's)
Featured in a December 1991 article in Fine Woodworking Magazine. Described in Stewart Coffin's book The Puzzling World of Polyhedral Dissections; here is some of what he says in the directions that came with the puzzle:"Special version - only one made. No half-pieces, so ignore puzzle problems that require half-pieces. The cube has only one solution in which all sides have matched wood and grain symmetry."The pieces are the eight ways to glue together a basic U-shaped piece; below are the pieces of the Interlocking puzzle version, the one made by Stewart Coffin pulled apart, and his grain pattern:



The wood and grain restriction has only one solution, but on the other hand, you are given clues how to do it. For example, there is just enough walnut to go around (a total of 8 squares), and so the solution cannot have any of the walnut squares hidden in the middle. For the single wood version, here is one of the solutions:




For the single wood version, Interlocking Puzzles said that there are 7 solutions each with a symmetric version; here is the solution sheet that was sold with the puzzle:
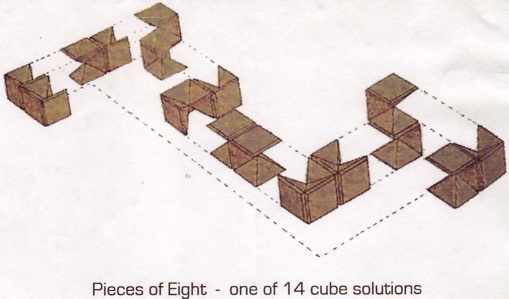


Designed Rick Eason 2004, purchased from Mr. Puzzle Australia 2006.
(Burdekin Plum, 2.4 inches)
The solution is unique and made more difficult due to 3 "false solutions" (arrangements that could exist in a solved state but there is no order of assembly to achieve any of them). Below are photos of two steps in the solution and the sheet that came with the puzzle:



Further reading:
Winter Patent, from: www.uspto.gov - patent no. 6,241,248


Designed by Rick Eason 2001, made by John Devost 2007.
(Bocote and Cherry, 4 pieces, 2.4 inches square;
as described on Rick Eason's Page, this puzzle was also mass produced as
"Confusion Puzzle Mental Block" shown on the right above - wood 2.9" square)
Four pieces formed from unit cubes and rods of dimensions 1/2 by 1/2 by 2.5 units.
The photos below show the four pieces positioned to be assembled, and pairs put together; the final step slides these two halves together to get the solved cube shown above.


Further Reading
Rick Eason's Page, from: http://www.mechanicalpuzzles.org/puzzles/index.html
Amazon: http://www.amazon.co.uk/Lagoon-CONFUSION-PUZZLE-MENTAL-BLOCK/dp/B004KYNB76

Designed by Kevin Holmes and Rik Van Grol, made by Eric Fuller 2009.
(Peruvian Walnut and Spalted Oak, 2.7 inches)
A beautiful and fun puzzle; here are photos of assembly:








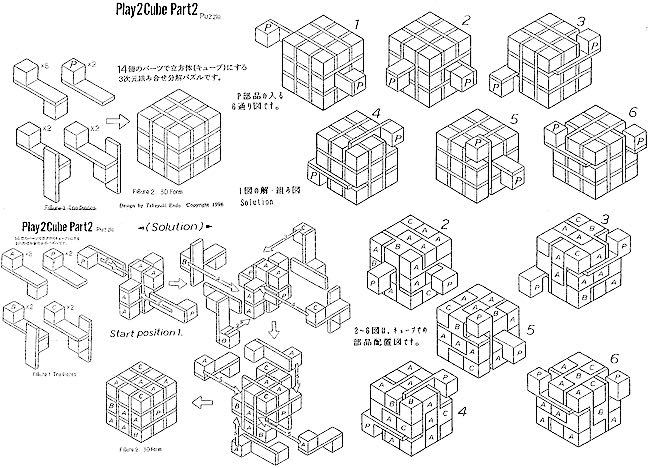
Made by Takeyuki Endo, 1996.
(cardboard box, 14 oak pieces, direction / solution sheet, 2.75"square)
Four different types of pieces, each a flat piece connecting unit size cubes, which can be assembled in six different ways to solve to a cube.

Designed by Markku Vesala, made by Eric Fuller 2016.
(Purpleheart with nylon dowels, 3 inches square)
Here is what the puzzle maker said:"The 3x3x3 cube is pretty played out. With only 27 units there are only so many things you can do with it. That's assuming tradition block glued to blocks...if you open up edge connections, a whole new world of complexity appears! Markku's excellent Liberal Cube makes good use of these dynamics, with a very confusing and difficult seven piece serial assembly. I would estimate that the difficulty is on par with Coffin's Convolution design which of course uses a 4x4x4 design format. This puzzle is a lot of fun and displays very well with the contrasting white dowels against the dark purpleheart."Here are 6 photos (not to scale) of the puzzle coming apart:

a.k.a. Magic Cube
Circa 2000.
(laminated cardboard with Andy Warhol art, 2.75 inches)
Unlike the Hinged Cubes puzzle, this puzzle is trivial to solve and is more of a toy than a puzzle. The cube shown above, can be unfolded in two different ways to form a 2 x 4 array, and then in both cases that 2 x 4 array can be folded lengthwise to form another 2 x 4 array:








Copyright James A. Storer 2009; U.S. patent 8,393,623 March 2013.
(Kingwood with brass hinges, 2.25 inches square assembled)
Fold the eight cubes into a larger 2x2x2 cube; there are seven hinges:

Hinge 1 joins cube 2 to cube 1, on the front faces.
Hinge 2 joins cube 3 to cube 2, on the back face of 3 and the right face of 2.
Hinge 3 joins cube 4 to cube 3, on the top faces.
Hinge 4 joins cube 5 to cube 4, on the front faces.
Hinge 5 joins cube 6 to cube 5, on the left face of 6 and the right face of 5.
Hinge 6 joins cube 7 to cube 6, on the back face of 7 and the front face of 6.
Hinge 7 joins cube 8 to cube 6, on the top faces.
Fun but not too hard; people often spend 30 minutes or so to solve. Solid hinges suggest folding one cube at a time, which can lead to a position like the one shown on the right above.
Construction has four types of hinge cutouts:Type A: Cube 1,7,8: Top-RightThe types can be arranged in this order and then rotated appropriately to attach hinges:
Type B: Cube 2,5: Top-Right, Left-Up
Type C: Cube 3,4: Top-Right, Back-Up
Type D: Cube 6: Top-Right, Front-Up, Left-Right1 2 3 4 5 6 7 8
A B C C B D A A
A Full 3D Print of the Hinged Cubes
Made by J. A. Storer, 2022 (2.25" square assembled; a 2" version was also made).
Prints the 8 cubes and then attaches the same brass hinges used for the original wood version, where precise cutouts and screw holes are made for the hinges.




Made by Andrew Soshea, 2022 (2.25" square assembled).
This clever design prints a fully working puzzle. The hinge pins have a tolerance around then so that no cracking of joints is needed after printing. The box is a separate fully working 3D print; writing on the box top and bottom is via a thin initial layer before changing colors.



a.k.a. Snake Cubes, Serpent Cubes, Cubra Cubes
Patented by Dryer U.S. 3,222,072 in 1965 and sold by Trench Puzzles circa 1985,
this one made by J. Storer 1988.
(bloodwood, 2.8 inches assembled)
Twenty seven cubes are threaded together with an elastic cord (the cord either pass through opposite faces or faces at 90 degrees). They can be folded up by rotating adjacent cubes with respect to each other to form a 3x3x3 cube (where none of the cord shows).
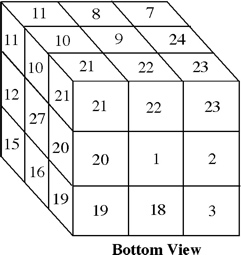
If the cube sequence was alternately colored red and black, then the solved 3x3x3 cube has red corners and face centers. Other puzzles are possible with different patterns or colors. The Kev solution is unique where the ends are face centers.
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/snakecube.htm
Mark Weston's Page, from: http://www.cs.uvic.ca/~mweston/snakes.html
Eryk Vershen's Page; from: http://cantaforda.com/cfcl/eryk/puzzles/chain_cube.html
Dreyer Patent, from: www.uspto.gov - patent no. 3,222,072
With the standard corded version, a cube can rotate in place due to the cord stretch. This 3D print version eliminates the cord and requires mechanical rotation of adjacent faces. One often needs to pre-rotate upcoming attached portions before a fold, thus precluding strictly sequential folding, and making it harder to visualize and quickly try out possibilities.
Referring to the figures on the preceding page, is convenient to solve by first positioning the three triples 25/26/27, 21/22/23, 19/20/21 and then working back to Cube 1. Cube 25 is the "Start Cube" (S), Cube 1 is the "End Cube" (E), "Bend Cubes" (B) turn the cord 90 degrees, and "Pass Cubes" (P) sends the cord straight through.
Cubes ordering can be represented as a character string broken up into the places where a P occurs and there are three cubes in a line (3 characters at the start and two places where 5 characters make a pair of them) to make substrings of lengths 3, 1, 5, 11, 5, 2:
The parts, based on 7/8" cubes, are Start, Bend, Pass, End, Peg, Plug:
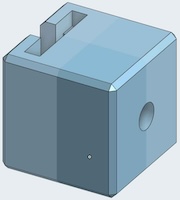

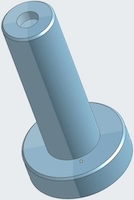
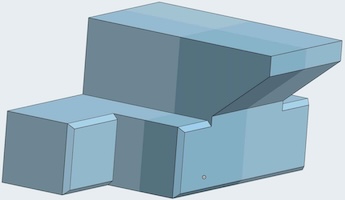
Pegs are pushed in as far as they will go (hole depth allows the head to protrude appropriately). A cube is attached by sliding its peg head into the slot of the adjacent cube and inserting a plug. Although glue could be used, tolerances are sufficiently tight for puzzle play. The tolerance of the peg heads allows a cube to spin freely (so long it is against a flat plane of cubes).
On the left below, the decorative version uses a second color for the plugs. On the right below, the solid color version uses a different print for the bend cube that hides the plugs; for the 5 pass cubes and the end cube the same color plug is used (and for the solved puzzle the 6 exposed plugs can be hidden by appropriately rotating those cubes).


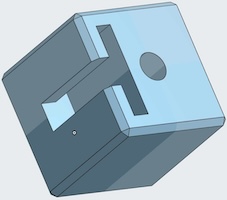

Plastic, 2+5/8" square when assembled, copyright J.A. Storer, 2023.

a.k.a. Snake Cubes, Serpent Cubes
Same idea as Kev's Snake Cubes, but a different pattern.
(2 inches square)
The Cubra Cubes are the same idea as Kev's Snake Cubes, but come in a number of different patterns; this is the first pattern shown on Mark Weston's Page:"A solution can be described by a string of "directions" that the cube follows when you wrap it into a cube, either Right, Left, Up, Down, Forward, or Back. So for example if a solution starts R R F L ... then put the end of the snake with the rest trailing off to the Right, then the next cube goes in the same direction (it must be a straight-through cube), the next cube (a corner cube) turns to point Forward, then it goes Left, etc."Unlike Kev's Cubes, a solution starts and ends in the corners, and is not unique. Here is a solution that is provided for the Lagoon version of this puzzle (the same as the first one above, with the directions R-L, F-B, U-D all reversed):
Solutions:
R R F L U U F D D R U B B L L F D F U U B B R R F F
R R U L F F U B B R F D D L L U B U F F D D R R U U"
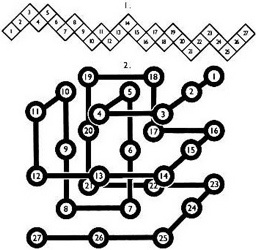
Further reading:
Mark Weston's Page, from: http://www.cs.uvic.ca/~mweston/snakes.html
Lagoon Solution, from: http://www.give-me-a-clue.com

Designed by Geoge Hart, published 2017.
(Printed on a Monoprice Mini V1 3D printer, from Thingiverse thing 2132796, 2019,
PLA plastic, 2" square)
Two pieces flow together to form a cube:

Further Reading
Helix Cube Thingiverse Page, from: http://www.thingiverse.com/thing:2132796

Packing puzzles typically require one to fit pieces into a tray (two dimensional) or a box (three dimensional), although sometimes the problem is to fit the pieces into a particular shape. Perhaps the most well known example, which as been around for centuries, is the tangram, where the goal is to use the same set of simple two dimensional shapes to make many different shapes.
a.k.a. All Square Novelty Puzzle, Check-A-Board, Tyr & Do It,




Famous Checkerboard Puzzle, Weekly Telegraph Chessboard Puzzle
Left: Made 1940's by a relative of J. A. Storer who lived in up-state New York.
(wood cigar box and painted pieces cut from 1/4" masonite, with 1" squares)
Right two: J. F. Friedel Co., Syracuse, N.Y, circa 1940's.
(6.5 by 8 by 1" cardboard box and 12 cardboard pieces with 1+3/8" squares;
top edge says "Mfg. by J. F. FREDEL CO. Syracuse N.Y.";
bottom edge says "MFGS. REPRESENTATIVES POTTER & REAGAN")
Arrange the pieces to make a standard 8 by 8 checkerboard. There are 10 distinct pieces and two of the 5-unit Z's. Shown on pages 70-73 of the Haubrich book, which lists a unique solution (shown above). Here is another version made in Great Britian:


All Square Novelty Puzzle, Frederick Warne & Co.,
London and NY, circa 1930's?
(6.25 x 6.25 x 13/16 inch cardboard box
and 12 wood pieces based on 15/16" squares 1/8 inch thick;
directions on the back of the box)
Note: Frederick Warne & Co. is the publisher of
the 1893 Hoffmann book.



Patented by H. Luers and made by Selchow & Righter, NY, circa 1880.
(8.5 inches square by 3/4 inch cardboard box and 15 cardboard pieces, 14 distinct;
pieces based on 1 inch squares can be arranged in the box;
on the cover and pages 217-219 of the Haubrich book,
which lists this puzzle having 6,013 solutions;
solution on the left above is from Haubrich, and right is from the Luers patent)
Left is a solution a previous owner drew inside the box bottom, right is the label on the box top, and below is the label inside the box top.



This version is nearly identical to the one shown on the previous pages, except the color of the label on the box top is a bit more brown than gray, and the pattern around the edge is a bit different (and this one has nothing inside the box top or bottom).





Phenyo-Caffein Co., Worcester, MA, circa 1900.
(5.25 inches square by 5/8 inch cardboard box and 15 cardboard pieces, 14 distinct;
pieces based on 5/8 inch squares can be arranged in the box;
also made with a wood box of the same dimensons and graphics)
The Pheno-Caffein Co. also made the Misfit 6 Piece Burr. The inside of the box bottom (on the right above) challenges the solver by stating that the dark square of the smallest piece can occupy any of the 32 dark squares. The sheet available from the company, on the next page, shows eight solutions (representing solution classes).

Further Reading
Luers Patent, from: www.uspto.gov - patent no. 231,963






a.k.a. Famous 'Bug House' Puzzle
Feltham Co., London, Royal Letters Patent 16,310, circa 1889.
(cardboard box and 14 thick cardboard pieces, 5" x 5" x 1/2";
box bottom has add for Feltham's tennis bat;
has a sheet that is the same as what is on the inside of the box bottom;
shown on pages 165-174 of the Haubrich book,
which gives the date and lists this puzzle as having 84 solutions; one is shown above)

Franco, NY, circa 1948.
(cardboard box and 14 distinct metal pieces, 3.25" x 3.25" x 1/2")

The Bug House Puzzle, E.I.H. Co. and F&K, 1912.
(cardboard box and 14 distinct metal pieces, 2.1 by 3.1 by 1/2 inches;
inside box top gives directions and manufacture;
shown on the cover and on pages 150-151 of the Haubrich book,
which gives the manufacture date,
identifies "E. I. Horsman Co." and "Forsheim & Koningsberg", NY,
and lists this puzzle as having 141 solutions, one of which is shown below)


Note: There were a number of variations of this puzzle made. This one is the same as page 150-151 of the Haubrich book if the pieces with dots in the photo above are taken to be black; however, the dots shown in the Haubrich book are not in the same locations.




Vasen Mfg. Co., Davenport, Iowa, 1928.
(cardboard box and 14 distinct cardboard pieces, 4.25 by 4.25 by 5/8 inches;
inside box bottom says you can send 10 cents to get three different solutions;
shown on pages 158-164 of the Haubrich book,
which lists this puzzle as having 84 solutions, one of which is shown above)
Note: Pages 165-174 of the Haubrich book show puzzles that are the same except for the colors reversed, and pages 183-187 of the Haubrich book include the same box top where if the pieces for those puzzles have the colors reversed, they are the same except for one (and the same as Xcel Checkerboard Puzzle No. 1).

Doyle Puzzle Co., Buffalo, NY, circa 1920?
(cardboard box 5.1"x5.1"x7/8", and 14 distinct cardboard pieces with 3/4" squares;
same as the Famous and Baffling Checkerboard Puzzle with colors reversed;
also made in a 13 piece version, the New XceL Checkerboard Puzzle No. 2;
shown on pages 183-187 of the Haubrich book,
which lists this puzzle as having 84 solutions, one of which is shown below)

Note: The Chequers Puzzle shown on page 97 of the 1893 Hoffmann Book is the same as a mirror image of this puzzle, except that puzzle shows only 63 squares, and can be corrected to make one of the three 4-unit L's be a 5-unit Z.

Doyle Puzzle Co., Buffalo, NY, circa 1920?
(cardboard box 5.1"x5.1"x7/8", and 13 distinct cardboard pieces with 3/4" squares;
also made in a 14 piece version, the XceL Checkerboard Puzzle No. 1;
shown on page 122 of the Haubrich book,
which lists this puzzle as having 7 solutions,
5 of which a composed of two 4 by 8 solutions,
one of these 5 and one other are shown below,
where the black squares correspond to green and the white to black)



Gyro Checker Board Jig Saw Puzzle, undated.
(3.5 by 6 inch envelope and 14 distinct cardboard pieces based on 1 inch squares;
shown on page 196 of the Haubrich book,
which lists this puzzle as having 598 solutions, one of which is shown below)



a.k.a. Krazee Checkerboard Puzzle, Zebas Puzzle,
Banzee Island Checkerboard Puzzle, 59-444 Checkerboard Puzzle
Peter Pan Playthings, England, circa 1950.
(plastic box and 12 plastic pieces, 4.75 by 4 by 5/16 inches;
there are 11 distinct pieces, where there are two of the 6-unit L;
shown on pages 57-65 of the Haubrich book, which gives the manufacture date
and list this puzzle as having 11 solutions, one of which is shown above;
pages 60-65 show reflected with reverse colors patented by J. Avila-Valdez 1995)
Arrange the pieces to make a standard 8 by 8 checkerboard. Paper, shown below, is glued to the bottom inside of the box that gives a layout for quickly storing the pieces unsolved in the box. The bottom of the box is a non-transparent black plastic that does not allow you to see the back of the paper. However, by holding it up to the light one can see that the reverse side of the paper has instructions similar to the Krazee Checkerboard Puzzle, shown on the following page.

Further Reading
Avila-Valdez Patent, from: www.uspto.gov - patent no. 5,403,005




Krazee Checkerboard Puzzle, Plas-Trix Co., Jamica, NY, 1957.
(plastic box and 12 plastic pieces, 4.75 by 4 by 5/16 inches;
same puzzle as the Draught Checkerboard Puzzle shown on the previous page,
but the back of the box is clear to allow one to view directions;
also shown on pages 57-58 of the Haubrich book, which gives the manufacture date)

Zebas Checkerboard Puzzle, Plas-Trix Co., Brooklyn, NY.
(plastic box and 12 plastic pieces, 4.75 by 4 by 5/16 inches;
same puzzle as the Krazee Checkerboard Puzzle shown on the previous page,
and also made by the Plas-Trix Co., but with different packaging)


Banzee Island Checkerboard Puzzle, made in Hong Kong.
(12 plastic pieces in plastic bag with cardboard top, 6.25 by 6.5 inches;
same puzzle as the Zebas Checkerboard Puzzle shown above,
the back of the package top refers to Chief Zebas)



S. Adams Co. Neptune, NJ., Copyright 1958.
(6" by 4" cardboard package and six 3.5 by 2.5 inch puzzles,
the checkerboard and five others, including Magic T;
shown on page 167 of the Adams Co. History book;
shown on page 21 of the Haubrich book.
which presents the unique solution shown above)




Made in Japan circa 1940.
(wood box 3.8 by 3.75 by 7/16 inches thick and 19 wood pieces;
wood inlays on the box cover are 5/8 inch diameter;
paper stamp on the back is 1/2 inch square)
Purchased from someone who remembered it from his childhood in the 1940's. At some point in the past the following solution was drawn:


This puzzle has the same dimensions, style, and cover inlays as the 16 piece puzzle on page 233 of the Haubrich book. However, even if one assumes that the 1x1 pieces broke off of larger ones before the solution above was drawn, and taking into account rotations and reflections (the pieces are double sided), there is no way to make it the same (and no way to further combine pieces to make it the same as the 14 piece puzzle of the same style on page 177) Here are the 16 pieces if the 1x1's are joined to the pieces above them in the solution above:

a.k.a. Caricature, Cut-Up Square, Stone Tangram,



Union Stone Puzzle, Richter Anchor Stone Puzzle No. 8
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3.1" x 3.1" x 9/16", 7 stone pieces, booklet, and solution booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1890;
described on pages 77-79, 96-97, 111-115, 128 of the 1893 Hoffmann book.
"casse tete" and "kopfzerbrecher" mean headache in French and German;
inside of the cover shows how to pack the pieces into the box;
inside of the box bottom has an add for "Dr. Richter's Pain-Expeller";
booklet has multi-language text inside covers and on pages A to Q at the front,
and 64 pages with 195 shapes to make,
where the last 16 pages are shapes made in combination with another puzzle;
second booklet has solutions)
An old design known as the Tangram, dating back to ancient China; seven tiles, called Tans, can be used to make different shapes. The Richter Company of Germany, known for stone building blocks, started making this puzzle and others in 1891. It is number 8 of over 36; see The Anchor Puzzle Book, The Tangram Book, Slocum and Botermans books, and also the Richter Summary later in these pages. Many versions of the tangram have been made, some packaged as two squares of half the area:

Richter (1846-1910) had a number of business besides stone building sets and puzzles, including selling medicines (see the Richter history on the Ankerstein Page). Many of the Richter puzzles have adds or testimonials to his pain medicine. The add below is on the inside of the box bottom of the puzzle on the preceding page.

The text on pages A to Q at the start of the booklet that precedes the 64 pages of shapes is very similar to that in versions of a number of other Richter puzzles (e.g., see the corresponding pages for the Tormentor and Pythagoras puzzles). Page L describes how the last 16 pages are shapes made in combination with another puzzle; shapes 180 to 183 use the Circular Puzzle, shapes 184 to 187 use the Tormentor, shapes 188 to 191 use the Cross Puzzle, and shapes 192 to 195 use Pythagoras. An English description similar to what is on Page L is given in the description that came with the "Puzzle Drive" version shown below.
































Note: These pages are shown in order (left to right, top to bottom), except that page 64 (pattern 195) is shown with page 1 (patterns 1 through 4).
This figure was extracted from the page scans shown on the preceding page; the patterns are in the order as in the booklet (left to right, top to bottom), except that page 64 (shape 195) is shown with page 1 (shapes 1 through 4).

The shapes on the first 48 pages need only the pieces of this puzzle. This figure was cropped from the figure of all shapes on the preceding page; the patterns are in the order as in the booklet (left to right, top to bottom), except that the last 4 patterns (page 48) are at the end of row 1.




(cardboard box 3.2 by 3.2 by 5/8 inches, 7 stone pieces, and two booklets;
the inside of the cover shows how to pack the pieces into the box;
box is constructed with a lip on the bottom,
booklet cover says "The Anchor Puzzle 3rd Ed",
booklet inside cover for "Casse-Tete Persan" and cover for "Kopfzerbrecher",
which says that this is the "third edition" at a price of "15 kr.",
is followed by a 3 page French and German introduction,
followed by unnumbered pages of shapes similar to the puzzle on the first page,
followed by a final page, in German, that advertizes Anchor blocks
by referring to the picture on the back of the booklet;
second booklet is a work book with shapes to draw in and many blank pages)



(cardboard box 3 by 3 by 9/16 inches, 7 stone pieces, and two booklets;
similar to the version on the previous page;
a more compact box where the small bottom lip is hidden when the cover is on;
box top graphics and booklet front and back (shown above) are the same;
inside box bottom advertizes "ANCHOR PAIN EXPELLER" from 1890;
booklet is basically the same except it is in German and English;
booklet inside cover for for "Kopfzerbrecher" and "The Anchor Puzzle",
which says that this is the "third edition" at a price of "10 cents",
followed by a 3 page German and English introduction,
followed by unnumbered pages of shapes similar to the puzzle on the first page,
folloed by a final page, in English, that advertizes Anchor blocks
by refering to the picture on the back of the booklet)





(cardboard box 3.1 by 3.1 by 1/2 inches, 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
box bottom lists other puzzles for sale,
the booklet has 64 pages of the same 195 shapes as the puzzle on the first page,
along with the single loose double sided page of English directions shown above)
some versions have the same box cover with "UNION" instead of "ANCHOR"
and the same booklet cover with just "STONE PUZZLE" on a single line)





(cardboard box 3.1 by 3.1 by 5/8 inches, 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
box and booklet front show copyright, and booklet back shows the U.S. manufacturer;
the booklet has text on the insides of the covers and 48 pages
of the same 179 shapes as the first 48 pages of shapes on the first page;
unlike earlier versions of this puzzle, an explicit copyright date is shown)


(cardboard box 3.1 by 3.1 by 9/16 inches, 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
the booklet has 64 pages of the same 195 shapes as the puzzle on the first page,
however its cover is blank, and there is no text explaining that
the last 16 pages are shapes made in combination with another puzzle;
the pages of this booklet were used for the scans shown earlier)


a.k.a. All Nine, Richter Anchor Stone Puzzle No. 1
F. Ad. Richter & Co., Germany, late 1890's / early 1900's
(cardboard box 2.7" x 4.4" x 1/2", 9 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1899;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 141 shapes to make,
the first of which is the star, which can be solved as shown above,
and where the last 16 pages are shapes made in combination with another puzzle)



(cardboard box 2.7" x 4.4" x 1/2", 9 stone pieces, and booklet;
booklet has the same shape pages as the one on the previous page,
but no additional text pages;
back of the box lists other puzzles)


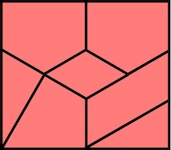
a.k.a. Richter Anchor Stone Puzzle No. 2
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3.1" x 3.6" x 9/16", 7 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1893;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 140 shapes to make;
where the last 16 pages are shapes made in combination with another puzzle;
the first four shapes are the rectangle, parallogram, triangle, and hexagon)


Same size box and booklet as version on the preceding page.
The booklet starts with 16 not numbered pages, where the first 12 are a page of directions in 12 different languages, and the last 4 pages have multi-language text with a coupon that could be mailed in along with 15 cents to get solutions to all of the problems. Following these 16 pages are 48 pages of the same problems as the version on the preceding page. The booklet front cover, inside of the front cover, inside of the back cover, and the back, present the same text in 12 different languages; on the inside of the back cover, the English text says "Second book to The "Lightning Conductor" for drawing in the lines of solved problems." So it would appear to be the second of two booklets that originally came with the puzzle.


Same size box and booklet as version on the preceding pages.
The booklet has 48 pages of the same problems as the version on the preceding pages.



(cardboard box 3.1" x 3.7" x 1/2", 7 stone pieces, and booklet;
German text on inside of front and back cover;
also has a loose sheet with directions in German;
same 48 pages with 140 shapes to make as puzzle on first page)
(same pieces but different shapes than Richter 16 Magic Egg)



a.k.a. a.k.a. Columbus' Egg, Columbian Puzzle, Richter Anchor Stone Puzzle No. 3
Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.1" x 4.1" x 9/16" with wood inserts, 9 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1893;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 111 shapes to make,
where the last 16 pages are shapes made in combination with another puzzle;
there are no graphics on the back of the booklet)



(cardboard box 3.1" x 4.1" x 1/2" with wood inserts, 9 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
the booklet has multi-language text inside the covers and on pages A to Q at the front,
and 32 pages with 95 shapes to make;
the booklet is the same as the one on the preceding page
except without the final 16 pages)




(cardboard box 4" x 3.5" x 5/8" with cardboard insert, 9 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
booklet has Spanish and Hungarian inside the front cover and German inside the back cover,
and at the front are 3 pages of Spanish directions and 4 pages of Hungarian directions,
48 pages present the same pages as the puzzle on the first page,
where the figures have a shaded green texture as shown above)


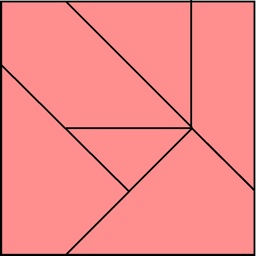
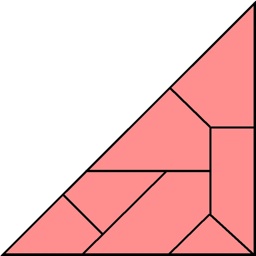
a.k.a. Richter Anchor Stone Puzzle No. 4
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 4.1" x 3.1" x 9/16", 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1896;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 130 shapes to make,
where the directions state that the first is the square using only 6 pieces,
the second is the right triangle of 3/2 the height of the square using only 7 pieces,
all others use all eight pieces,
and where the last 16 pages are shapes made in combination with another puzzle)


(cardboard box 3.1" x 4.1" x 1/2", 8 stone pieces, and booklet;
similar booklet with the same shapes as the version on the previous page)




(cardboard box 3.25" x 4.1" x 9/16", 8 stone pieces, and booklet;
same problem pages as the versions on the preceding pages,
but with no front or back matter, except for a loose double sided page
tucked under the cover - front and back shown above)


a.k.a. Richter Anchor Stone Puzzle No. 5
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3" x 3.6" x 9/16", 7 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1893;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 108 shapes to make,
where the last 16 pages are shapes made in combination with another puzzle)



(cardboard box 3" x 3.6" x 9/16", 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text on pages A to Q at the front,
and 48 pages with the same 108 shapes to make as the puzzle on the preceding page)


(cardboard box 3" x 3.6" x 9/16", 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
this one is missing the booklet;
it came with some extra cardboard pieces
that are in the bottom of the box below the stone pieces)




(cardboard box 3" x 3.6" x 9/16", 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
booklet has 48 pages with the same 108 shapes to make as the preceding pages)




a.k.a. Richter Anchor Stone Puzzle No. 6
F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 3.5" x 3.5" x 9/16", 9 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1911;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 32 pages with 98 shapes to make;
the text above is on the box bottom under the puzzle)





Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.5" x 3.5" x 9/16", 9 stone pieces, and booklet;
booklet has the same 32 pages with 98 shapes to make
as the puzzle of the first page, but no additional text;
included is one loose double sided page of text)


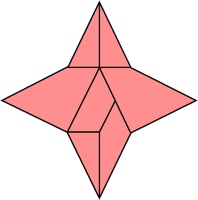
a.k.a. Goblin, Richter Anchor Stone Puzzle No. 7
F. Ad. Richter & Co., Germany, late 1890's / early 1900's
(cardboard box 3" x 4" x 9/16", 7 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1899;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 143 shapes to make;
where the last 16 pages are shapes made in combination with another puzzle;
a previous owner has penceled in a solution to the first problem shown above)


(cardboard box 3" x 4" x 9/16", 7 stone pieces, and booklet)
The inside of the cover shows how to pack the pieces into the box;
booklet shows the same shapes as the puzzle on the previous page,
but includes no text.


a.k.a. Richter Anchor Stone Puzzle No. 9
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3.6" x 3.6" x 9/16", 10 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1891;
described on pages 85-87, 120-121 of the 1893 Hoffmann book;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 121 shapes to make;
where the last 16 pages are shapes made in combination with another puzzle)



Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.6" x 3.6" x 9/16", 10 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
the booklet starts with 8 pages of multi-language text,
followed by 48 pages of the same 121 shapes as the puzzle on the first page;
this box top was made with a number of variations a b of the text for different markets)





Richter Co., circa 1890's / early 1900's.
(cardboard box 3.7" x 3.7" x 9/16", 10 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
box bottom lists other puzzles for sale,
booklet has 48 pages of the same 121 shapes as the puzzle on the first page,
along with the single loose double sided page of English directions shown above)

a.k.a. Sherlock Holmes, Hi Ho, Richter Anchor Stone Puzzle No. 10





F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3" x 3.75" x 9/16", 7 stone pieces, and two booklets;
the Anchor Puzzle Book dates this puzzle as first made in 1892;
described on page 83-85, 118-119 of the Hoffmann book;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the inside of the bottom has a testimonial dated 1899,
variations of this testimonial appear in the box top or bottom other versions;
first booklet has multi-language text inside covers and on pages A to Q at the front,
and 48 pages with 149 shapes to make
the first of which is the cross as shown above,
and where the last 16 pages are shapes made in combination with another puzzle;
the second booklet gives a solution for each shape)



Same dimensions as version on the first page;
the inside of the cover shows how to pack the pieces into the box;
booklet has nothing on the inside covers,
with 8 unnumbered pages of multi-language text,
followed by the same 48 pages of problems as the version on the first page;
the first page credits Dr. Richter's Publishing House, 215 Pearl St., NY;
second booklet is the same solution booklet as the one on the first page.



Same dimensions as version on the first page;



box construction uses a lip on the bottom;
the inside of the cover shows how to pack the pieces into the box;
inside of the bottom has a testimonial dated 1890;
inside covers and first 8 unnumbered pages have multi-language text,
followed by 48 pages with the same problems as the version on the first page;
however, the problems are drawn with black line art rather than red coloring;
the first page of problems is shown to the right of the booklet cover above;
second booklet has solutions for problems on the first 32 pages.
Note: Version shown on the top right is Dutch version; it says "Kruisraadsel" at the bottom of the box top and on the front cover of the booklet (which has the identical pages).


Same puzzle as the one shown on the first page;
3" x 3.7" x 1/2";
booklet has the same 48 shapes to make,
but without the text pages at the front and back.


a.k.a. Richter Anchor Stone Puzzle No. 11
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3.1" x 3.1" x 5/8", 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1894;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has 8 pages of multi-language text at the beginning,
and 32 pages with 89 shapes to make)



Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.1" x 3.1" x 9/16", 8 stone pieces,
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside covers and on pages A to Q at the front,
and 32 pages with 89 shapes to make, same as those on the preceding page)


Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.1" x 3.1" x 5/8", 8 stone pieces,
and booklet of 32 pages with the same 89 shapes as the preceding page)



a.k.a. a.k.a. Richter Anchor Stone Puzzle No. 12
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3 by 3 by 9/16 inches, 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1891;
described on pages 81-83, 117-118 of the 1893 Hoffmann book;
similar in construction to the Anchor Puzzle Tangram;
the inside of the box cover shows how to pack the pieces into the box;
the inside of the box bottom has a testimonial dated 1899;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 64 pages of 197 shapes to make,
where the last 16 pages are shapes made in combination with another puzzle)
Described on page L of the booklet, the last 16 pages are shapes made in combination with another puzzle; shapes 182 to 185 use the Anchor Puzzle, shapes 186 to 189 use the Tormentor, shapes 190 to 193 use the Circular Puzzle, and shapes 194 to 197 use the Cross Puzzle.
































Note: These pages are shown in order (left to right, top to bottom), except that page 64 (pattern 197) is shown with page 1 (patterns 1 through 3).
Here are the front and back cover, the inside front cover, pages A through Q that come before the problem pages, and the inside back cover. The text in German, French, and English discusses this and other puzzles, and gives testimony from a satisfied customer.















Similar to the version on the first page, but
box has different construction with a lip on the bottom,
booklet has multi-language text on inside covers and 6 unnumbered pages,
and the booklet has the same problems but drawn with black and white art
(first three pages of problems shown above)




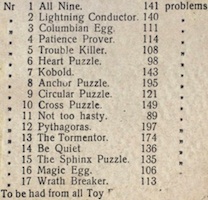
Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.1 by 3.1 by 1/2 inches, 8 stone pieces, and booklet;
the inside of the box cover shows how to pack the pieces into the box;
the booklet has the same 64 pages with 197 shapes to make as the puzzle on the first page,
where the last 16 pages are shapes made in combination with another puzzle,
and the extra double-sided sheet describes them)



Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3 by 3 by 1/2 inches, 8 stone pieces, and booklet;
the cover slides on;
the booklet is 48 pages of 181 puzzles;
these 48 pages are the same as the first 48 pages of the puzzle on the first page;
there is an extra double-sided text page in German between pages 18 and 19,
that seems to be a bit out of place because it discusses
the combinations that would be on the other 16 pages)



a.k.a. Richter Anchor Stone Puzzle 13
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3 by 3 by 9/16 inches, 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1891;
described on pages 80-81 of the 1893 Hoffmann book;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the inside of the bottom has a testimonial dated 1899;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 64 pages with 174 shapes to make,
where the last 16 pages are shapes made in combination with another puzzle)
Described on page L of the booklet, the last 16 pages are shapes made in combination with another puzzle; shapes 159 to 162 use the Circular Puzzle, shapes 163 to 166 use the Anchor Puzzle, shapes 167 to 170 use the Cross Puzzle, and shapes 171 to 174 use Pythagoras.
































Note: These pages are shown in order (left to right, top to bottom), except that page 64 (pattern 174) is shown with page 1 (patterns 1 through 4).
Here are the front and back cover, the inside front cover, pages A through Q that come before the problem pages, and the inside back cover. The text in German, French, and English discusses this and other puzzles, and gives testimony from a satisfied customer.












Same as the version on the first page
except for the art on the box top and the front and back of the booklet
(same box top inside, testimonial, booklet text and problems).





Similar to the version above, but
box has different construction with a lip on the bottom,
booklet has multi-language text on inside covers and 8 unnumbered pages,
and the booklet has the same problems but drawn with black and white art;
the first three pages of problems are shown above.




(cardboard box 3.1 by 3.1 by 1/2 inches, 8 stone pieces, and booklet;
inside of the box cover shows how to pack the pieces into the box;
booklet has the same 64 pages with 174 shapes as the puzzle shown on the first page,
where the two sided instruction sheet describes the puzzle)



a.k.a. Richter Anchor Stone Puzzle No. 14 (sometimes 3)
F. Ad. Richter & Co., Germany, late 1890's / early 1900's
(cardboard box 3" x 3+7/8" x 1/2", 10 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1899;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has 48 pages with 136 shapes to make,
where the last 16 pages are shapes made in combination with another puzzle;
the solution to the first problem in the booklet is shown above)
Note: Although usually referred to with the number 14, some versions of the box graphics showed the number 3.


a.k.a. Richter Anchor Stone Puzzle No. 14 /3
Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3" x 3+78" x 1/2", 10 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
booklet has 48 pages with the same 136 shapes to make as the preceding page)


a.k.a. Richter Anchor Stone Puzzle No. 14 /3
Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3" x 3+78" x 1/2", 10 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
booklet has 48 pages with the same 136 shapes to make as the preceding pages)

a.k.a. Lott's Stone Puzzle, Anchor Puzzle No. 15 (sometimes 16)


F. Ad. Richter & Co., Germany, late 1890's / early 1900's
(cardboard box 2.7" x 4.4" x 9/16", 7 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1899;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
a second way of packing the pieces into the box is shown by the figure above;
the inside of the bottom has a testimonial dated 1899;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 135 shapes to make,
the first of which is the pyramid of square root 3 times the height of the rectangle,
and where the last 16 pages are shapes made in combination with another puzzle;
Note: The box above does not show a number. However this puzzle was commonly listed by in Richter literature as number 15, and 15 appears on the boxes of some versions. It was also made with a box that has the same graphics as the one above with "No. 16." above the word Sphinx.




Puzzle pieces the same as the first page but box is 2.75" x 4.9" x 1/2";
booklet has the same 48 pages of problems but no additional text;
the inside of the cover shows how to pack the pieces into the box;
directions are on a separate two sided sheet that is slightly smaller than booklet pages.




Puzzle pieces the same as the first page;
booklet has the same 48 pages of problems but no additional text;
the inside of the cover shows how to pack the pieces into the box;
directions are on a separate two sided sheet that is slightly smaller than booklet pages.


"Lott's Stone Puzzle", copyright 1911, Lott's Bricks, LTD, Watford, England.
(cardboard box 2.7" x 4.2" x 9/16", 7 stone pieces, and booklet;
the booklet pages 1 and 2 are an introduction,
the last page invites one to write for a solution to another puzzle,
and pages 3 through 31 show 105 shapes to make,
where page 31 shows the rectangle for how to pack the pieces into the box)
(same pieces but different shapes than Richter 3 Egg Of Columbus)


a.k.a. Miracle Egg, Richter Anchor Stone Puzzle No. 16 (sometimes 17)
F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 3.1" x 4.1" x 9/16" with wood inserts, 9 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1912;
booklet has 48 pages with the same 106 shapes to make
as the puzzle on the following page, but without the other pages of text)



Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.1" x 4.1" x 9/16" with wood inserts, 9 stone pieces, and booklet;
also made with the similar box top but without "No. 17",
the inside of the cover shows how to pack the pieces into the box;
the booklet has multi-language text inside the covers and on pages A to Y at the front,
and 48 pages with the same 106 shapes to make as puzzle in preceding page;
the first page of shapes has written "Copyright Nachdruck verboten";
all shapes use only the 9 pieces of the puzzle;
the booklet names each shape in pages A to Y)


a.k.a. Richter Anchor Puzzle No. 17
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3.5" x 3.5" x 9/16", 7 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1893;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 113 shapes to make,
where the last 16 pages are shapes made in combination with another puzzle)



Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.5" x 3.5" x 9/16", 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text on eight unumbered pages at the front,
and 48 pages with the same 113 shapes to make as the puzzle on the previous page,
where the last 16 pages are shapes made in combination with another puzzle;
this Gnome theme box top was made with different variations of the text)


Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.5" x 3.5" x 9/16", 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
the booklet has the same 48 pages with 113 shapes to make
as the puzzle on the first page, but with no additional directions)




Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.5" x 3.5" x 9/16", 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
the booklet has the same 48 pages with 113 shapes to make
as the puzzle on the first page, but with no additional directions);
two addition directions sheets are included)
Archimedes


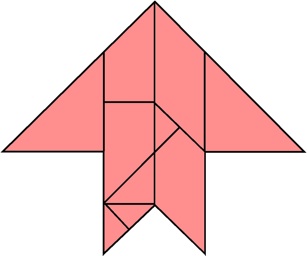
F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 3.2" x 4.3" x 9/16", 9 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside covers and on pages I to XIX at front,
where none of the text is in English,
followed by a blank page where a previous owner has drawn
a solution to the additional shape shown above,
followed by 32 pages with 97 shapes to make)
Bose Siben (Nasty Seven)



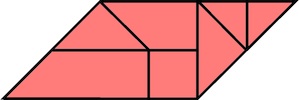
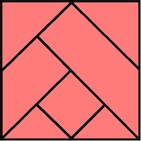
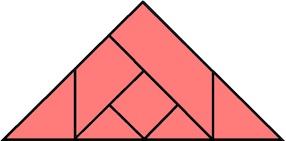


F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 2.25" x 4.25" x 1/2", 7 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has English text on the inside of the covers shown above,
and 32 pages with 99 shapes to make,
where the first is the rectangle for the box packing
and next three are the parallelogram, square, and triangle shown above)
Ritze Ratze (Razzle Dazzle)



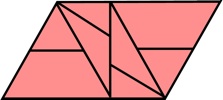


F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 2.75" x 3.7" x 1/2", 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has English text on the inside of the covers shown above,
and 32 pages with 98 shapes to make,
where the first is the rectangle for the box packing
and the second is the parallelogram shown above)
Frisch Gewagt (Have Courage)





F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 2+11/16" x 4.25" x 1/2", 9 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has English text on the inside of the covers shown above,
and 32 pages with 96 shapes to make,
where the first is the shape for the box packing
and the second is the rectangle shown above)
Zeitvertreiber (Pastime)





F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 2.5" x 4.5" x 1/2", 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has English text on the inside of the covers shown above,
and 32 pages with 96 shapes to make,
where the first is the rectangle for the box packing
Zeppelin





F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 2.75" x 3.7" x 1/2", 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has English text on the inside of the covers shown above,
and 32 pages with 98 shapes to make,
where the first is the rectangle for the box packing
and the second is the parallelogram shown above)
Kiebitz-Ei (Lapwing Bird's Egg)



F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 3+7/16" x 3+5/8" x 1/2", 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has 19 pages of text in multiple languages,
and 32 pages with 96 shapes to make,
where the first is the box packing shown above;
a scan of the booklet is shown on the following pages)
Teufeldien (Little Devil)



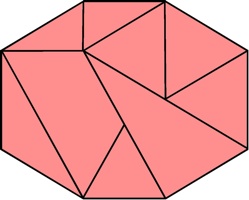


F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 2.75" x 3.7" x 1/2", 9 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has English text on the inside of the covers shown above,
and 32 pages with 96 shapes to make,
where the first is the rectangle for the box packing
and the second is the octagon shown above)
Heureka (Eureka)



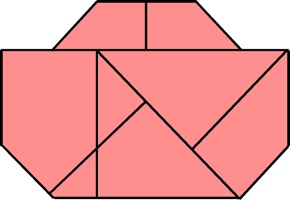


F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 3.1" x 3.75" x 1/2", 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has English text on the inside of the covers shown above,
and 32 pages with 96 shapes to make,
where the first is the rectangle for the box packing
and the second is the shape shown above;
label across front is from F. A. O. Swartz, N.Y.)
The manufacture for the Richter Anchor Puzzles began in the 1890's, where the puzzles numbered above 17 were made in the World War I era. The 1893 Hoffmann book describes the Anchor, Circular, Cross, Pythagoras, and Tormentor puzzles (and also the Star Puzzle). A history of the Richter puzzles is presented in The Anchor Puzzle Book by Jerry Slocum (see also the Slocum and Botermans books). The puzzle boxes were made with a variety of cover art (see the following page), although the stone pieces, made with the Richter Co. patented process, are the same. Perhaps what made these puzzles so popular were the fun booklets that came with them, giving a host of shapes to make.
Here is a booklet that came with the Anchor Puzzle, and also a corresponding solution booklet that one could purchase by mail:


Generally, booklets have more or less the same cover art as the box top, but not always. For example, on the left and middle are booklets for versions of the Tormentor and Cross Puzzle that look very different from the corresponding box top, and on the right is a booklet for a version of the Anchor Puzzle that has blank covers (and nothing inside besides the problem figures):



Here are two examples of additional work booklets that came with the Anchor and Lightning Conductor puzzles:


Some box themes were highly regular; here are some examples (the last one in the first row is used on boxes numbered above 17, and the others for 17 and below, where the last three in the second row are dated in the The Anchor Puzzle Book as relatively late versions first made in 1922, 1925, and 1932 respectively):








Other themes used fun graphics (e.g., people thinking, specialized graphics, cartoons); here are some examples (all used on puzzles numbered 17 and below):















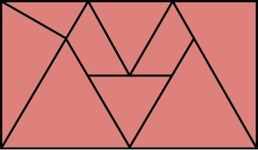
Richter 1
The Nine
Richter 2
Lightning Conductor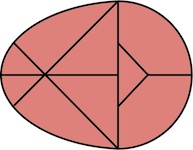
Richter 3
Egg Of Columbus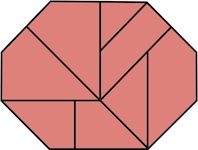
Richter 4
Patience Prover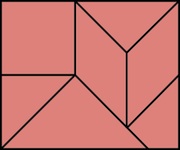
Richter 5
Trouble Killer
Richter 6
Heart Puzzle
Richter 7
Kobold
Richter 8
Anchor Puzzle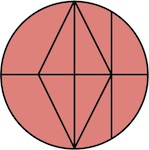
Richter 9
Circular Puzzle
Richter 10
"Cross Puzzle"
Richter 11
Not Too Hasty
Richter 12
Pythagoras
Richter 13
Tormentor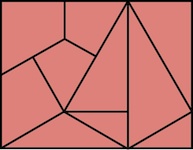
Richter 14
Be Quiet
Richter 15
Sphinx
Richter 16
Magic Egg
Richter 17
Wrath Breaker
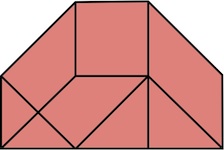
Richter 18
Archimedes
Richter 19
Ende Gut, Alles Gut
Richter 20
Pass Auf
Richter 21
Eile mit Weile
Richter 22
Sorenbrecher
Richter 23
Kopernikus
Richter 24
Pyramide
Richter 25
Nur Mut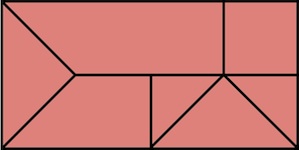
Richter 26
Bose Siben
Richter 27
Ritze Ratze
Richter 28
Frisch Gewagt
Richter 29
Zeitvertreiber
Richter 30
Zeppelin
Richter 31
Kiebitz-Ei
Richter 32
Wer Wegt Gewinnt
Richter 33
Fur Kluge Leute
Richter 34
Hexenmeister
Richter 35
Teufeldien
Richter 36
Heureka
Here are pages from an old Richter Brochure (courtesy of Jerry Slocum, Puzzles Old And New, Copyright 1986, page 28); see also The Anchor Puzzle Book by Jerry Slocum.

Here (and on the following page) are the shapes used to make the 36 Richter Anchor Puzzles (courtesy of Jerry Slocum, Puzzles Old And New, Copyright 1986, page 28); see also The Anchor Puzzle Book by Jerry Slocum.
(second half of the figure from Puzzles Old And New, Copyright 1986, page 28)
The Anchor Puzzle Book, from: http://www.SlocumPuzzles.com
Richter Company U.S. Brochure, from: http://www.cs.brandeis.edu/~storer/JimPuzzles/ZPAGES/zzzRichterBrochure.html
Anker Page, from: http://www.ankerstein.org
Richter History, from: http://www.ankerstein.org/html/CO.HTM
Wikipedia Tangram Page, from: http://en.wikipedia.org/wiki/Tangram
Rubiks.com Double Tangram booklet, from: http://www.rubiks.com/World/Rubiks%20downloads.aspx
Rob's Tangram Page, from: http://home.comcast.net/~stegmann/tangram.htm
Slocum Database, from: http://webapp1.dlib.indiana.edu/images/search.htm?scope=lilly/slocum





a.k.a. Richter Picco Nr. T1
F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 2.125" x 2.125" x 3/8", 8 stone pieces, and problem sheet;
the Anchor Puzzle Book dates this puzzle as first made in 1913;
puzzle tray slides into the right side of the box with a small tab to pull it out;
top and bottom of box edge says "Richter Rudolstadt";
same pieces in a smaller size as Richter 13 Tormentor;
problem sheet has 26 shapes, where problem 11 shows how to pack into the box)
The first of three miniature Richter puzzles referred to as Picco or Piccolo (Nr. T2 is the same as Richter 12 Pythagoras; and Nr. T3 is the same as Richter 8 Anchor Puzzle; with the parallelogram piece divided into two triangles); see the Anchor Puzzle Book.
Further Reading
Indiana Slocum Archive (photos of Picco versions of Nr. T1 Nr. T2 a b c, Nr. T3 a b) from:http://webapp1.dlib.indiana.edu/images/search.htm?scope=lilly/slocum





a.k.a. Richter Hamleys
F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 2.125" x 2.125" x 3/8", 8 stone pieces, and problem sheet;
puzzle tray slides into the right side of the box with a small table to pull it out;
same pieces in a smaller size as Richter 13 Tormentor;
same size and pieces as Richter Piccolo Nr. T1, and like that puzzle,
problem sheet has the same 26 shapes, where problem 11 shows how to pack into the box)
Further Reading
Modern page of the London Hamleys toy store: from: http://www.hamleys.com/explore-stores.irs

"Schutzengraben-Geduldspeil"

"Zoologischer-Garten"
Richter Company, Germany, early 1900's.
(both puzzles cardboard box 3.1" x 3.1" x 1/2", 15 stone pieces, and problem sheet)
These two puzzles are the same except for the included direction sheet. The Anchor Puzzle Book describes the 1915 Trench Puzzle as made for World War I soldiers, and the 1916 Zoo Puzzle as a "neutral" puzzle made in Switzerland.





Richter Company, Germany, 1890's / early 1900's.
(cardboard box 3.75" x 3.75" x 1/2", 48 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1892;
described on pages 87-90, 122-124 of the 1893 Hoffmann Book;
16 white right triangles, 8 white wedges, 8 black wedges, 16 black quadralaterals;
inside of the cover shows how to pack the pieces into the box;
inside of the box bottom has an add for "Dr. Richter's Pain-Expeller";
booklet has multi-language text inside covers and on pages A to Q at the front,
and 48 pages with 153 shapes to make)
Like Blumenspiel (using curved pieces) and Meteor One (using marbles), more of a two-dimensional building set than a puzzle.























--- 330 --- Star Puzzle, Continued


Different box and booklet cover art from the puzzle of the preceding page,
but otherwise the same)



Richter Company, Germany, circa 1915.
(cardboard box 8.8" x 8.8" x 5/8", 52 colored stone pieces, 6.75" x 6.75",
with 12 page blue problem and green solution booklets of 36 patterns)
More of a two-dimensional building set than a puzzle. Described on page 86 of the Anchor Puzzle Book, this is one of a number of Richter "Mosiac" puzzles made in the World War I time period that used colored tiles. The tiles are colored differently on each side; below is shown the arrangement shown above flipped over (in the horizontal direction), and two sample pages from the problem and solution booklets:



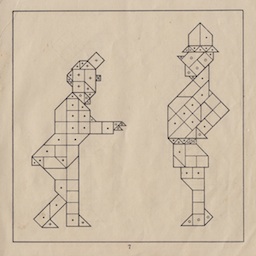

F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 6.3 by 6.3 by 5/7 inches, 4 colors marbles, and booklet;
more of a game than a puzzle, the object is to arrange the marbles into patterns;
in Richter's Puzzles and Pastimes catalog - see Anchor Puzzle references)






F. Ad. Richter & Co., Germany, early 1900's.
(wood box 8.75" x 8.75" x 2.5", 6 colors marbles, and booklet;
like Meteor 1, arrange the marbles into patterns;
also includes a Nine Mens Morris, board;
in Richter's Puzzles and Pastimes catalog - see Anchor Puzzle references)

a.k.a. Richter Anchor Puzzle
Wood puzzle purchased circa 2000; sleeve made by J. A Storer.
(wood tray and pieces with cardboard sleeve, 5+78" square by 3/8" thick)
The sleeve has the problems from the classic Richter Anchor puzzle:


"Wm. F. Drueke & Sons, Grand Rapids, Mich.", circa 1940?
(cardboard box 2.5 by 5.75 by 13/16 inch thick, and 7 wood pieces;
assembles to a 4.1 inch square by 5/16 inches thick)

Tryne Games Mfg. Inc., Lindenhurst, NY, copyright 1961.
(cardboard box 5.6 by 9 by 7/8 inch thick, booklet, and 7 plastic pieces;
assembles to a 5.4 inch square by 3/16 inches thick;
the problems in the booklet are similar to the Richter 8 Anchor Puzzle booklet; this puzzle should not be confused with Richter 12 Pythagoras)
(Same pieces as Richter No. 10 Cross Puzzle)

Kogner Bros. Inc., Tryne Game Division, East Paterson, N.J., circa 1960's.
(cardboard box 5.6" x 9" x 13/16" with plastic tray, booklet, and 7 plastic pieces;
assembles to a 5.4 inch square by 3/16 inches thick;
the problems in the booklet are similar to the Richter 10 Cross Puzzle booklet;
the box and booklet are not dated,
but the booklet references a copyright 1961 version of the Tangram that it calls "Pythagoras")
(Same pieces as Richter No. 10 Cross Puzzle)

Hi Ho Puzzle, 1932.
(2.75 by 2.5 by 5/8 inch cardboard box, 7 plastic pieces, and directions)
The pieces are made from Bakelite (an old type of plastic developed in the early 1900's). Below are the top and bottom edges of the box and one of the sides (the other side is the same). The directions show a sitting dog and suggest that many other patterns can be made.




Further Reading
Wilipedia Bakelite Page, from: http://en.wikipedia.org/wiki/Bakelite
(Same pieces as Richter No. 10 Cross Puzzle)


Sherlock Holmes Puzzle, circa 1960.
(2.9" x 3.6" x 7/16" plastic box, 7 plastic pieces, and directions;
the next page shows another copy still glued to the original 8.2" x 6.25" card)
(Same pieces as Richter No. 3 and Richter No. 16)




Scrambled Egg, Copyright ThinkFun 2002.
(9 metal pieces in plastic tray, 4 by 3.5 by 5/16 inches;
puzzle comes with clear plastic sleeve for storage;
booklet slides into tray bottom, and presents problems with solutions shown above)





Carrom Co., Ludington, Michigan, circa 1920s?
(cardboard box and 7 wood pieces, 3.6 inches square by 9/16 inches thick)
Like the Anchor Puzzle Tangram, the directions that were sold with this puzzle give a host of patterns to make from seven pieces similar to those of the Tangram.





ELZZUP Puzzle Co., Keene, N.H., circa 1900.
(3.3" x 3.3" x 3/4" wood box and 10 wood pieces)
This puzzle was sold in 2011 by a person who said it had been owned by Eleanor Dows of Laurel Mass., the sister of his grandfather, who was born in 1890. The back of the box top has her name in pencil, and her name and the town of Laurel Mass. is burned into the box bottom. The arrangment of the pieces into a square is not unique. In the spirit of the Anchor Puzzle Tangram, the goal is to make fun patterns with the pieces.







Wm. F. Drueke & Sons, Grand Rapids, MI, circa 1940's - 1960's.
(top: cardboard box 3.2"x3.2"x1/2", problem booklet, and 10 wood pieces;
middle: plastic box 8"x8"x1.2", problem & solution booklets, 10 wood pieces;
bottom: cardboard box 7.5"x7.5"x3/4", problem & solution booklets, 10 wood pieces)
In the same theme as the Anchor Puzzle Tangram, all three of these versions present 57 pages of 200 shapes to make. The first version above has only a problem booklet, which also includes English, French, and Spanish pages at the beginning that indicate that the puzzle may be purchased by mail for 50 cents, and that a solution booklet can be ordered for 25 cents; the back of this booklet shows how to pack the pieces into the box.
(from the 8x8" version)





























(from the 8x8" version)

































PIC-TUR-ETT Company, Mattapan, Massachusetts;
"PATENT APPLIED FOR"; all figures on directions and cards are copyright 1933.
(cardboard box, direction sheet, 15 problem ad solution cards, 4.25" x 4.25" x 1"))


Rockford Pattern Works, circa 1930's?
(4.25" square by 5/8" thick box, 9 wood pieces, and 4" square booklet;
some versions have the Rinehimer Millwork label on the box top)
Like the Anchor Puzzle Tangram, a booklet shows shapes to make. Here are the booklet pages (page 1 and the last page are shown together):












Further Reading
King Tut Wikipedia Page, from: http://en.wikipedia.org/wiki/King_tut
Rockford Foundries History, from: www.rockfordfoundries.com/about.cfm



German text on the package promotes Vision 2000; purchased 2010.
(cardboard box and four 7/16" thick wood pieces, 9.25" x 1.8" by 9/16")
In the theme of the Anchor Puzzle Tangram, using the same four pieces as the Missing T puzzle, the booklet gives 100 shapes to make, the first how to pack into the box and the last is the T:
















Further Reading
Vision 2000 Page, from: http://www.vision2020.org/main.cfm


Copyright ThinkFun 2008.
(plastic, 5" x 5" x 1.4")
In the theme of the Anchor Puzzle Tangram, 14 pieces can be arranged into many shapes. The box has a tray that slides out with 60 problem cards of shapes to make (that give hints and solutions on the back).
Further Reading
Problem card backs.

a.k.a. F Puzzle
Old design, 3D print files made by Fernando Jerez, 2016.
(Printed on a Monoprice Mini V1 3D printer at scale 160%,
from Thingiverse thing 2975065, 2019,
PLA plastic, 4 pieces and tray 2+1/4" x 3+3/4" x 3/16" inches)
An easy puzzle to pack the four F's into the tray:

Further Reading
Four F's Puzzle Thingiverse Page, from: http://www.thingiverse.com/thing:1666559

Magic Square, circa 1960?
(plastic box 2.5 by 1.75 by 1/2 inches and 4 plastic pieces;
assembles to a 2.5 inch square)

a.k.a. Square Me, Five Block Puzzle, Madagascar Madness
ThinkFun Binary Arts, 2003.
(plastic, 4-piece square is 3 inches, solved 5-piece square is 3.2 inches square)
People often quickly find the four piece solution and then get stuck trying "stretch" the puzzle just a little bit in a way that will accommodate an additional small square piece. If the four piece solution is 4 units square, it has area 16, the extra square has area 2, and the five piece solution has area 18 (forming a square that is just under 4.25 units square); for each of the pieces in the four piece solution, its orientation is 45 degrees counter-clockwise in the five piece solution:
Characterized on page 102 of the 1942 Filipiak book Filipiak book as "recorded in the records of antiquity", has been periodically made as a promotional item.

CSPI promotional circa 1975.
(plastic, solved 5-piece 2.9 inches square;
this was a company that J. A. Storer's father was a part of in the 1970's;
came with a wire loop which J. A. Storer replaced in 2007 with Snowbird key ring)


"Madagascar Madness", Behavioral Sciences Inc., 1969.
(5 inches square by 3/4 inch thick plastic box and five plastic pieces;
the square piece was lost and replaced with a green plexi-glass piece)
This puzzle is packaged with a tray for the 4-piece solution and the 5th piece loose; perhaps to guide the solvers thinking away from the 5-piece solution. The directions on a 4.5 inch square card inserted into the back give an interesting discussion of the geometry:

Further reading
Dickinson's Witch Hazel promotional, unknown age.
(3" x 4.5" envelope with cardboard pieces, solved 5-piece square is 4" square;
Dickinson's Witch Hazel was first made in 1866 and was still being made in 2000)

Five Block Puzzle, S.S. Adams Co. circa 1950?
(1/4 inch thick wood pieces, solved 5-piece square is 5 inches square)
http://www.lib.uconn.edu/online/research/speclib/ASC/findaids/
EEDickinson/MSS19960001.html

Designed by Wladimir Krasnouchow, distributed by Puzzle Master 2019; cardboard sleeve added by J. A. Storer.
(plastic, 4+3/16 x 3+11/16 x 1/4, the circle is .57 inches diameter)
In a theme like the classic Double Square puzzle, this clever puzzle presents the seemingly impossible task to pack the red circle inside the frame together with the five pieces. That is, somehow you have to get the red circle to fit into this already crowded tray:

One having seen the solution, is unlikely to forget it. If you are frustrated, here is a hint (shown upside down so it won't read it by mistake):



a.k.a. T Puzzle, Magic T, Cut-Up T, Pa's T Puzzle,
Great American T Puzzle, White Rose Ceylon Perfect T Puzzle, Lash Bitters T Puzzle.
Old design, copyright 1898 Lash Inc., this copyright ThinkFun Binary Arts 2003.
(plastic, 4 pieces, 3.1" high by 3" wide when solved)
The four pieces can be positioned to form a T as shown above. The HIQU puzzle has a booklet of problems based on these pieces. This is an old puzzle that has been produced many times; here is a nice antique wood one:

Pa's T Puzzle, circa 1940's.
(cardboard box 4.6 by 1.75 by 11/16 inches and 4 walnut pieces,
5" high by 4.75" wide when solved;
box edge says "PA'S T PUZZLE No. P 20 WM. F. DRUEKE & SONS Grand Rapide, Mich.")

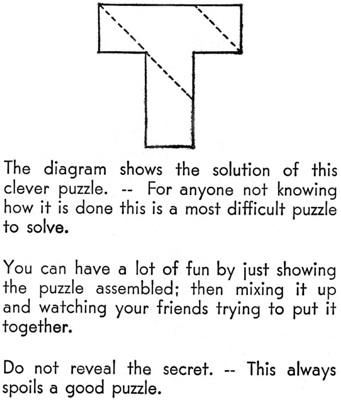
S. S. Adams Co., circa 1950's.
(3.5" cardboard sleeve with cardboard directions and dark green plastic pieces)

Magic T Puzzle, unknown manufacture.
(plastic box 2.5 by 1.75 by 1/2 inches and 4 plastic pieces)
Marx Toys, circa 1960's.



(5.5 by 7 inch cardboard card with plastic pieces;
solution sheet in plastic bag and big question mark with company logo behind the bag)
Further Reading
T Puzzle Wikipedia Page, from: http://en.wikipedia.org/wiki/T_puzzle



"Shackman N.Y.1 No. 3627 Cross Puzzle", made in Japan, circa 1960's?
(cardboard box 5+1/8" x 1.75" x 5/8", direction sheet, and six 1/8" thick wood pieces
consisting of four identical Z shapes and two identical L shapes;
assembled cross is 4+3/8" high by 3 inches wide at the cross, and 1" wide at the tips.)


Hikimi Nob Yoshigahara Puzzle Collection, Japan, Copyright 1987.
(box and 6 wood pieces, 3.7" x 6.1" x 3/4";
included are directions in Japanese that give the problems shown above)

Designed by T. Linden, made by E. Fuller, 2009.
(velour bag and 7 English Brown Oak pieces, 3 inches assembled)
There are two 1x1x3 unit pieces each with one 45 degree pointed tip, three 1x1x2 unit pieces each with one 45 degree pointed tip, and two unit triangles.
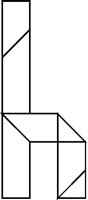
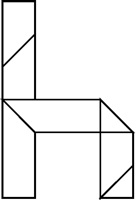
By cheating just a little bit, an upper case H can also be formed. On the left below the upper right tip of the H is missing a unit triangle. In the middle, the pieces have all been rotated 90 degrees and are arranged so that the H looks perfect from above (it is formed from two 3 unit pieces on the left, two triangles for the cross, and three 2 unit pieces on the right, where there is a missing triangle on the top right tip when viewed from the side). On right below, again the pieces have all been rotated 90 degrees and are arranged so that the H looks perfect from above (it is formed from a 2 and 3 unit piece on each side, a 2 unit piece and a triangle for the cross, and the remaining triangle filling in one of the tips, with the other three tips having a missing unit triangle when viewed from the side).
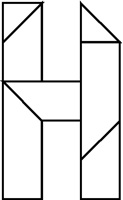


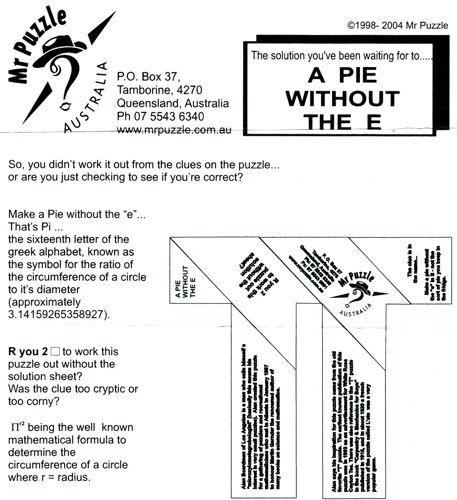
Promotional puzzle from Mr. Puzzle Australia, 2008.
(6 thin flexible plastic pieces)



Made by interlocking Puzzles 2000.
(directions card and 6 identical Zebrawood pieces, each 2.25 inches)
Here is what Interlocking Puzzles said:"There are at least eighteen different challenges requiring the special angles and three, four, five, or six pieces of our Make a Square puzzle. Geometric shapes possible include triangles, squares, rectangles, pentagons, hexagons, parallelograms, and trapezoids. This tiling puzzle seems simple, but it is quite challenging to find all the solutions. These 6 pieces are each over 2 inches long, which allows the largest finished shape to be over 7 inches across the diagonal."

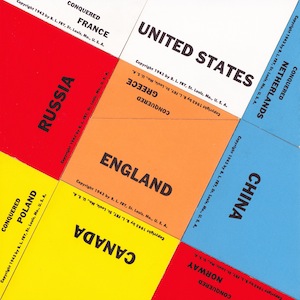
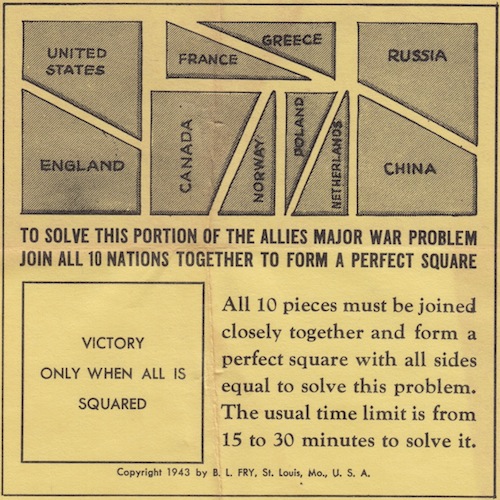
Copyright B. L. Frye, St. Louis, MO, 1943.
(5 identical shaped large cardboard pieces and 5 identical shaped smaller cardboard pieces,
in a cardboard envelope 3+5/8" x 3+7/8", with directions on the inside)



Designed and mad by Stewart Coffin, 2013
(maple and paduk on a plywood bottom, 3.7 x 3.7 x 3/4", signed on the bottom;
one of 4 puzzles purchased during a visit with the designer in 2014)
Shown on page 155 of the Coffin AP-ART book. This puzzle is already a challenge due to the number of pieces and that they are two sided. Also, when it is given to someone with the pieces out of the box, there is a natural tendency to put them in so that they fit tight into the corners, in which case one inevitably ends up with having two pieces left that will not fit into the final corner. It is only after noticing that although the pieces are precisely cut, space is left between the packing and sides of the frame, and so something seems wrong (in fact, that space is equal to the space in the corners when the puzzle is correctly solved).


Designed by Stewart Coffin, made by Eric Fuller 2013.
(Ebony, Canarywood, Sapele, acrylic plastic top, 3.75" x 3.75" x 7/8";
6 puzzle pieces with the shapes shown above)
The plastic top has some rectilinear openings through which the pieces can be inserted and manipulated. Remove the pieces, mix them up, and then re-insert them. The underside has a rim that allows one to play with piece assembly without the plastic on top. Here is what the puzzle maker says:"I've constructed this with a solid Sapele body, shouldered on the corners for strength. The acrylic top is precision cut on the laser and the bottom is a solid floating canarywood panel chosen for contrast against the dark ebony. The fit is precise, with rounded corners to enable the very tricky rotational solution."The puzzle maker also quotes from the designer:"The three puzzles in this category all have a 5x5 square two-sided tray. On the back side is a simple framed square for practice exercises. The front side has a Plexiglas cover with openings cut in it through which the puzzle pieces are inserted. Of these three, The Decoy (#187-A) is by far the most difficult and my favorite. It is the only one that requires a slightly loose tray or rounding of corners to solve."
Plas-Trix Co., Jamica, NY, circa late 1950's



(plastic box and 12 plastic pieces, 4.75 by 4 by 5/16 inches)
Made by the same company and packaged like the Krazee Checkerboard Puzzle and the Krazee Links, but easier. Here are the packing instructions on the back of the directions and a solution:


Purchased 2004.
(wood base with metal pins, 7 wood pieces, 5 inches)
A board with metal pins must have 7 wood pieces (with holes) placed on it to form a square. The solution is not unique.



Copyright ThinkFun 2008.
(plastic, 3 inches)
Pack the four T's into the square. On the left above is the top side of the puzzle solved, and on the right above is the easier underside of the puzzle (with a larger square) solved.

Designed by E. Nagata, copyright Binary Arts 2002.
(plastic and metal, 3.5 by 4.5 by 3/8 inches thick)
The puzzle comes with the pencils placed on one side of the board as shown above. The challenge is to flip the board over and pack them into the other side:


Designed by Bill Cutler, made by Walt Hoppe, and purchased 2006.
(15 pieces including the pearl and shell, 4.5 inches)
The goal is to place the thirteen wedge shaped pieces and the pearl (the little round piece) into the shell. After achieving the configuration shown above, the pearl is off to the right in the keeper hole, the pieces meet at a point in the center, and there appears to be no extra space. Now for the fun; the pieces can all be flipped over and space made to place the pearl in the center of the shell:


Designed by Bill Cutler and made by Walt and Chris Hoppe, 2008.
(25 wood pieces, each 3/16 inch thick, solved puzzle is 6.5 inch diameter circle)
Pack the 25 pieces to form a circle; here is what the directions say:"These pieces can be used to tile the plane non-periodically. They are a variation of the Penrose "Kites and Darts" tiles. Each barn is equivalent to the Penrose "Dart" piece, and the silos and tractors are each one-half of a "Kite" piece."The graphics on the 25 pieces are:(5) barn with a siloFurther Reading
(5) barn with a double silo
(5) barn (no silo) with a tractor
(5) barn (no silo) with a tractor towing a cart
(3) barn with a double silo and tractor
(2) barn with a silo and tractor towing a cart
Note: The directions say that some puzzles were made with the quanties 3 and 2 reversed.
Wikipedia Penrose Tiling Page, from: http://en.wikipedia.org/wiki/Penrose_tiling

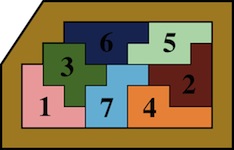
Designed by Minoru Abe, purchased 2014.
(cardboard box, wood tray, and seven wood pieces)
Find all 7 ways to pack the 7 pieces, each consisting of 6 unit squares, into the tray that is 5 units high by 9 units wide with 3 units blocked out in the upper left corner; one is shown above, and here are the six others:
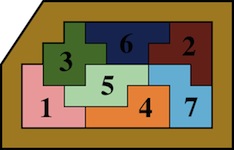
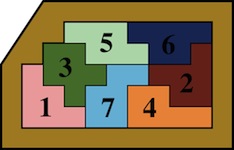
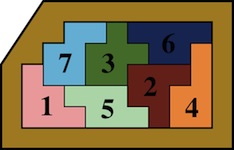
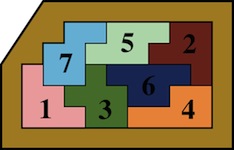

a.k.a. Polyominoes
Old puzzle, this one made by Yasumi, 1995.
(wood, box and 12 pieces based on 0.75" inch cubes)
The 12 distinct shapes formed from 5 connected squares are the pentominoes (called polyominoes by Solomon W. Golomb, Charles Scribner's Sons, NY, 1965):
Total area is 60, and sizes 6 x 10, 5 x 12, 4 x 15, and 3 x 20 can be formed. There are known to be 2,339 distinct ways to form a 6 x 10 rectangle, excluding rotations and reflections. In contrast, there are 1,010 solutions for 5x12, 368 solutions for 4x15, and 3 x 20 has a unique solution except for rotating a central portion by 180 degrees.
A piece is landlocked if it does not touch one of the borders of the rectangle. Eric Harshbarger has determined that there are no 6x10 rectangle solutions with 5 or more landlocked pieces, but there can be solutions with 0, 1, 2, 3, or 4 landlocked pieces (e.g., there are 207 solutions of the 6x10 rectangle with four landlocked pieces, 1,111 with three, 864 with 2, 155 with one, and only a couple with zero).
R. M. Robinson of the University of California at Berkeley proposed the "triplication problem": Given a pentomino, use 9 of the other pentominoes to construct a scale model, 3 times as wide and 3 times as high as the given piece (all 12 are possible).
Pentominoes are traditionally flat pieces that can be arranged to form 2-dimensional patterns. However, if the pieces are made to be 1-unit thick, then fun 3-dimensional patterns can also be made, including a 3 x 4 x 5 solid, and stairs that are 6 wide by 4 deep by 4 high.
(The shaded area of the 3x20 solution may be rotated by 180 degrees.)

From the directions sold with the Yasumi version:
From the directions sold with the Interlocking Puzzles version:


Made By B. Cutler, 1989.
(3.25"x4"x2.375" plastic box and 12 two-color wood pieces with 3/4" cubes)
Can be used like any other pentominoes set. In addition, it is made from light and dark woods so that it can be solved in a 3x4x5 box where colors have a checkerboard pattern on all sides. Here is the diagram of the pieces from the directions that came with the puzzle:
Sold with this puzzle was printout of a number of solutions. Here is the one suggested; the pieces have the names 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, and this figure shows the three planes of the checkerbox:ABB5C A666C A636C
BB555 A7778 3333C
B9958 A9778 9944C
11111 22228 44428
From the directions sold with the Yasumi version:
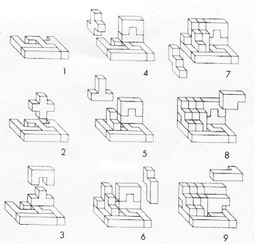
Shown on Nivasch's Page:
Further Reading
Harshbarger's Page, from: http://www.ericharshbarger.org/pentominoes
Mathworld Page, from: http://mathworld.wolfram.com/Pentomino.html
CIMT Page, from: http://www.cimt.plymouth.ac.uk/resources/puzzles/pentoes/pentoint.htm
Gerard's Page, from: http://www.xs4all.nl/~gp/pentomino.html
Huttlin's Page, from: http://members.aol.com/huttlin/pentominoes.html
Nivasch's Page, from: http://yucs.org/~gnivasch/pentomino
Mark's Page, from: http://mathsevangelist.wordpress.com/2012/08/24/packing-pentominoes
Jankok's Page, from: http://homepages.cwi.nl/~jankok/etc/Polyomino.html
info Page, from: http://www.theory.csc.uvic.ca/~cos/inf/misc/PentInfo.html
Gottfriedville Page, from: http://www.gottfriedville.net/puzzles/colorgame/solutions.htm
Belgium Pentominoe page, from: http://home.scarlet.be/~demeod/indexe.html
Puzzle Will Be Played page, from: http://www.asahi-net.or.jp/~rh5k-isn/Puzzle
Fletcher's Page, from: http://www.andrews.edu/~calkins/math/pentos.htm
Wikipedia Page, from: http://en.wikipedia.org/wiki/Pentomino
Negahban Design Patent, from: www.uspto.gov - patent no. 385,311
Further reading about some related puzzles:
Lester Patent, from: www.uspto.gov - patent no. 1,290,761
Wadsworth Patent, from: www.uspto.gov - patent no. 3,964,749
Sarkar Patent, from: www.uspto.gov - patent no. 5,544,882

Designed by P. F. Ramos 2004, made by Interlocking Puzzles.
(wood frame and 12 pieces, 3.75" x 3.75" x 3" inches)
Standard pentominoes are the 12 different planar shapes that can be formed from 5 squares. There are 17 non-planar pentomino shapes (each made from 5 cubes). Here, 12 of them (which can be can be grouped into 6 mirror image pairs) must be packed into a 4x5x5 box frame; 40 units are used by the frame, leaving exactly 60 units of space to pack these pieces:
According to the sheet that came with the puzzle there are 54,189 possible ways these pieces can fit (in the sense that you could build the box around them), of which 23,549 of them can be achieved by starting with the box frame and inserting and moving pieces. Here is the layer by layer representation of the solution that came with the puzzle (X is the box):
A
B
C
D
E
F
G
H
I
J
K
LIn the orientations shown in the figures above, pieces can be inserted as follows:
top layer:
XXXXX
XJAFX
XJJFX
XCCFX
XXXXX2nd layer:
XGAIX
GGAFF
GJAAK
HJCDK
XDDDX3rd layer:
XGBIX
BBBII
EEELL
HHCKK
XDCKXbottom layer:
XXXXX
XBEIX
XHELX
XHLLX
XXXXX
1. B from behind.
2. I from behind.
3. G from behind.
4. E from below.5. H from below.
6. A from behind.
7. L from the right.
8. K from the front.9. F from behind.
10. C from above.
11. J from the top.
12. D from the front.







a.k.a. Sneaky Squares, Stark Raving Cubes, Block Out, Square Fit, KUBI
Designed by Bill Cutler, wood version made by J. Devost, 1983.
(left: oak, 4.5 inches square by 2.25 inches high;
middle: Sneaky Squares / Start Raving Cubes, plastic, 4.5" square by 2" high;
right: Block Out / Square Fit, 3" square by 1.25" high)
Four pieces cut at odd angles (so that they not quite cubes) must be placed into the box (a three piece version has also been made). Inserting one at a time will not work. To solve, arrange them on the table so that the top is level and square, push them together at the bottoms, and drop them into the box. Here is what the pieces look like in their solved positions, outside the box:


a.k.a. The Third Degree
Designed by Bill Cutler, made by W. Hoppe, 1995.
(wood, 3.75 inches by 1.75 inches high)
Three pieces that are cut at odd angles (so that they not quite the same) must be placed into the box. Like the larger Block Head puzzle, putting them in one at a time will not work; to solve, first arrange them on the table so that the top surface is level and a hexagon, and then push them together at the bottoms and drop them into the box. Here is what the pieces look like in their solved positions, outside the box:


Designed and made by Stewart Coffin, 2014.
(maple pieces and sides on plywood base, signed on the bottom;
2.25" high, top edges of walls are 2", balls are 3/4" diameter;
one of 4 puzzles purchased during a visit with the designer in 2014)
Unpacking requires moving the top two pieces out of the way and removing the bottom one first:





Elverson Puzzle, 2002.
(wood box and 13 wood rods, 2.75 by 7.5 by 1.75 inches)
Pack 13 wood rods into the box. Here are th directions on the bottom of the box:

Here is the solved top layer taken out, showing the solved bottom layer in the box:


Made in the U.K., circa 2000?
(wood box and 18 wood rods, 2.7" square, with recessed silver dot stickers)
Pack the 18 rods into the box. A solution of 6 layers going from top to bottom is shown here from upper left to lower right (note that the rods of the top layer shown in the upper left all need to be rotated 180 degrees, as does the first rod in the second layer):



Copyright Pacific Game Company Inc., Japan, 1970.
(plastic, 3.25" square)
The object is to pull out all the pegs, mix them up, and reassemble. The instruction booklet shown on the following pages says there are 12 ways to do it, shows how to do two of them, and gives blank diagrams to color in the other ten solutions. Here is the solved cube shown above flipped over to show the other three sides:


Designed by John Conway, copyright ThinkFun Binary Arts 2003.
(plastic, box and 9 pieces, 1.75" solved)
Also known as Conway's Curious Cube, and described on pages 736-737 of the Winning Ways books. Three unit cubes and six 1x2x2 pieces must be placed in a 3x3x3 box. In the unique solution, the three unit cubes line up diagionally through the cube from a corner to the center to the opposite corner:


Here is the solution that was sold with the puzzle:



"BRADLEY'S, CUBE ROOT BLOCKS, No. 2, TO TWO PLACES", circa 1940?
(wood box and 15 pieces, 3.25" square;
pieces based on 1/2 unit cubes;
two unit size cubes, one 3x3x3 cube, and three each of 1x1x3, 1x1x4, 1x3x3, 1x4x4)

Designer unknown, made by and computer analysis done by Bill Cutler 1979.
(wood box and 18 wood pieces, 4.8" by 6.8" by 1.7" thick)
A box of inside dimensions 18 x 28 x 6 units into which must be placed 18 two unit thick pieces of sizes 4x9, (2) 5x9, 5x18, 5x21, 6x7, 6x10, 6x13, (2) 7x8, (2) 7x13, 7x18, 8x18, 9x11, 9x13, 10x11, and 11x11. Cutler's analysis showed four solutions (not counting rotations and reflections), all placing the 4x9, 6x7, and 6x13 pieces on end. Here is one of them, from the sheets that came with the puzzle (copyright by and courtesy of Bill Cutler).
top layer middle layer bottom layer
Exchanging the middle and bottom layers gives a second solution, and these two solutions each have an alternate version by exchanging the 7x18, 5x21, 6x10 pieces on the top layer with the 7x13, 5x18, 10x11 pieces on the middle layer.


Designed by Bill Cutler with a computer 1992, made by Tom Lensch 2004.
(Wenge box with Bubinga pieces, 5 inches)
Here are the layers of the unique solution, from the sheet that was sold with the puzzle (copyright by and courtesy of Bill Cutler):

A host of puzzles have been made that require the solver to match adjacent edges or faces based on colors or patterns. Perhaps the most famous example of this type of puzzle is Instant Insanity, where one must line up four colored cubes so that each side has all four colors.

a.k.a. Rubik's Mini Tangle
Circa 1990, this one by J. A. Storer 2007 from a Rubik's Tangle 5x5.
(nine 2" cardboard squares in a 2.75 by 4 by 3/4 inch plastic box)
Arrange 9 squares in a 3x3 array so that edges match. Each square has the same pattern of 4 tangled ropes that has two connections on each edge. Different squares have a different combination of the four colors (red, green, blue, and yellow).
Jaap's Page indicates that this puzzle may have been produced as a give-away to promote the Rubik's Tangle 5x5 puzzle. The puzzle pictured here was made by using squares from a Rubik's Tangle 5x5. It's solution is the upper left 3x3 portion of the first solution to Version 1:
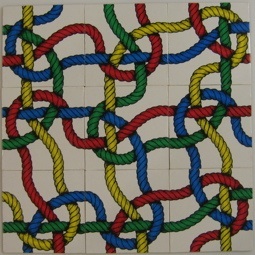
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles
Thurston Patent, from: www.uspto.gov - patent no. 487,798
Rankin Patent, from: www.uspto.gov - patent no. 606,338

Produced in 1995.
(nine 2" square plastic pieces, patterns on both sides)
Arrange 9 squares in a 3x3 array so that edges match. Each square has on both sides the same pattern of 4 tangled ropes that has two connections on each edge. Different sides of different squares have a different combination of the four colors (red, green, blue, and yellow). More confusing than Rubik's Tangle 3x3 because one has to decide how to flip the pieces.
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/tangle.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/r90/tangle.htm
Thurston Patent, from: www.uspto.gov - patent no. 487,798




Rubik's Tangle 1, 2, 3, and 4, Matchbox 1990.
(Box and twenty seven 2 inch cardboard squares.)
Arrange 25 squares in a 5x5 array so that edges match. Each square has the same pattern of 4 tangled ropes that has two connections on each edge. There is one square for each of the 24 possible combinations of the 4 colors (red, green, blue, and yellow), and one duplicate square. The only difference between Rubik's Tangle 5x5 Versions 1, 2, 3, and 4 is which piece is duplicated. By taking three pieces from a spare set, a single set of 28 squares can be made where three of the duplicates are left out to make one of the 4 puzzles. Below is a set made by starting with a Version 3 and adding three squares taken from a Version 2; the four duplicate squares have been labeled with a number on the back.



Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/tangle.htm
Thurston Patent, from: www.uspto.gov - patent no. 487,798
Rankin Patent, from: www.uspto.gov - patent no. 606,338


"Made in West Germany" by Haba.
(3.75" x 3.75" x 1.8" cardboard box with nine wood pieces, each 1.75" x 1.75" x 7/16")
If the solution shown is rotated 135 degrees clockwise then it corresponds to the figure on the cover by mapping the four characters to the colors of the puzzle (in fact, by looking carefully, one can see a resemblance between the characters and the actual colored figures of the puzzle).



Price, Stern, Sloan Inc., Los Angeles, CA; Pig and Frog 1989, Train 1991.
(3.25 by 5.4 by 5/8 inch cardboard box and nine 3 inch cardboard pieces)
Like Rubik's Tangle 3x3, the directions on the back ask you to arrange the nine squares in a 3 by 3 array so that adjacent edges match; the Crazy Train directions state that there are exactly two solutions and are written in both English and Spanish.




Copyright 1997 McDonalds, GamesCo.
(cardboard box containing nine 5" square cardboard pieces)



McDonald Land Guzzle - "Birdie"



McDonald Land Guzzle - "Grimace"



McDonald Land Guzzle - "Bus"




a.k.a. Infants' Hospital - The Magic Line
Chad Valley Co. Ltd., Harborne, England, 1920;
made for the Infants Hospital in Vincent Square, London, founded by R. Mond.
(cardboard box and 16 cardboard pieces, 7" x 6.25" x 1/2";
instructions on the underside of the box top;
based on a 6x6 grid with four 1x3 pieces, and 12 1x2 pieces;
see also Infants' Hospital Puzzle, Dad's Puzzler - Exchange Version / Infants Hospital, A Ward In The Infants' Hospital, Infants' Hospital Jigsaw Puzzle)
The goal is to make the line go continuously from the start position at the bottom and end at the special "HEALTH" piece. Don't view at the solution before you try it; it's harder than it looks.