Jim Storer


Burrs - 22
Knot Shaped Three Piece Burrs
Wood Knot - 28
Grooved Three Piece Board Burr - 29
Cross Keys (a.k.a. Three Piece Puzzle) - 30
Knotted Cube - 31
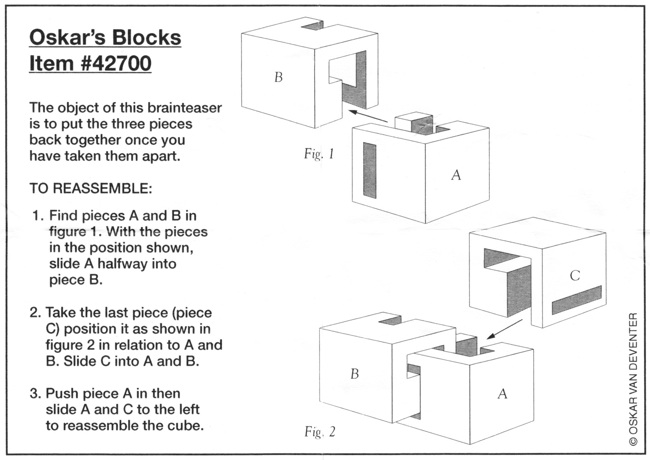
Oskar's Blocks - 32
Shaekel Knot - 33
Cheers - 34
Standard Shaped Three Piece Burrs With A Single Trick
Segerblom Knot - 35
Slideways Burr - 36
Sonneveld Three Piece Burr - 37
Triple Play - 38
Standard Shaped Three Piece Burrs
Just The Three - 39
Just 3 - 40
3 Piece Burr Yamaosa - 41
Three Open Windows - 42
GigaBurr & GigaBurr II - 43
Cubie Burr & Cubie Burr #2 - 44
Burrs With Four Pieces
JA6PB - Just Another 6-Piece Burr - 45
Accordion - 46
Burrs With Five Pieces
Disguised Burr - 47
Switch Board Burr - 48
Rift - 49
La Taupe - 50
Octo Burr - 51
Standard Six Piece Burrs
Simple 6-Piece Burr - 52
The Puzzle (a.k.a. Double Cross) - 54
Mikado Block Puzzle - 56
Yamato Block Puzzle - 58
Devil's Knot - 59
Misfit Puzzle - 60
Coffin's Improved Burr - 62
Bill's Baffling Burr - 63
L5 Notchable - 64
Computer's Choice 3-Hole - 65
Computer's Choice 4-Hole - 66
Eight Is Enough - 67
Compter's Choice 5-Hole - 69
The Piston Puzzle - 70
Computer's Choice Unique-10 - 71
L46AA Notchable - 72
Mega Six - 73
Love's Dozen - 74
139 Burr - 75
Non-Standard Six Piece Burrs
Twelve Points To Insanity - 76
Dragon Fly - 77
Butterfly - 78
Explode-A-Burr - 79
Programmer's Nightmare - 80
Holey Astigmatism - 81
NOS No. 7 - Seizaine - 82
U-Nam-It Burr - 83
Bill's Ball Bearing Burr - 84
Blind Burr - 85
Luxemburr - 86
Brass Monkey 2 - 87
Around The Bend - 88
Frantix - 89
Dovetail Burr - 90
Lock Nut - 91
Three Pieces Puzzle - 92
Tri Again - 93
Zauberflote - 94
Zig-Zag Knot - 95
Amulet - 96
Combined Burr - 97
Knotted Burr - 98
Six Piece Plate Burrs
Chen's Six Board Burr - 99
Chocolate Dip Burr - 100
Gordian Knot - 101
Bent Board Burr #2 - 102
Burrs With More Than Six Pieces
Japanese Shape Burrs (a.k.a. Kumiki Puzzles) - 103
Drueke Burrs - Bill's and Marian's Puzzles - 105
Missing Notch - 106
Uranus - 107
Gaia - 108
Elena's Burr - 109
Miyako Wooden Puzzle - 110
The Aeroplane Block Puzzle - 111
Sydney Harburr Bridge - 112
Bill's Ball Buster - 113
Hectix (a.k.a. Hexsticks, Notched Hexagonal Sticks) - 114
Locked Blocks - 116
Block Puzzle Senior - 117
Satellite Burr - 118
H Burr - 119
Sears Tower - 121
Wausau '81 - 122
Wausau '82 - 123
Wausau 83 - 124
Wausau 84 - 125
Burry Joint - 126
Lassen Risti - 127
Old Oak Of England - 128
Lattice - 129
Quadlock1 - 130
The Pacco Puzzle - 131
Q.E.D. - 132
Miyako 21-Piece - 133
Binary Burr - 134
Visible Burr - 135
SM24 Burr - 139
Multi Burrs
Fusion Burr - 148
Four Burr Stick - 149
Four Burrs - 151
Lost Day (a.k.a Eight Burrs) - 152
Berserk BurrCirc - 153
Framed Burrs
Oskar's Cube - 155
Two Piece Oddity - 156
Pair Dance - 157
Trapped Duo - 158
Three Sticks Trapped - 159
Three Trapped Sages - 160
Pandora's Box (a.k.a. Internal Combustion) - 161
Spacemine - 164
Locked Sticks - 165
Two Halves Cage - 166
Constrained Burrs - 167
Burr Sets
Simple 6-Piece 6-Solutions Burr Set - 168
Burr Set JCC - 169
CCH Level 1 Key Piece Burr Set - 170
Interlocking Puzzles Burr Set - 172
Interlocking Puzzles Burr Set #2 - 177
Cube Assembly - 180
Pieces Made from Unit Size Cubes
Soma Cube - 181
Half Hour - 182
IP Five Piece Cube - 183
Coffin Quartet - 184
Four X - 185
Bedlam Cube - 186
Century Cube - 187
Pieces Made from Rectilinear Non-Cubic Shapes
Patio Block - 189
Patio Block MPA - 190
Splitting Headache - 192
Pieces Based on Polyhedral Dissections
Quadro Cube - 193
Diagonal Cube - 194
Slideways - 195
Apparently Impossible Cube - 196
Pieces With Interlocking Connections
Cubes And Pegs - 197
Cubes And Pegs Version B - 198
L-Bert Hall - 199
Five Minute Puzzle - 200
Corner Block - 201
Pieces Of Eight - 202
Groovy Cubes - 204
Twenty Cube - 205
Rik's Kiddy Wrapping - 206
Play2CubePart2 - 207
Liberal Cube - 208
Manipulation of Connected Cubes
Folding Cubes - 209
Hinged Cubes - 210
Snake Cubes (a.k.a. Kev's Cubes, Serpent Cubes, Cubra Cubes) - 212
Misc Cube Assemblies
Helix Cube - 217
Packing (including 2D Shapes) - 218
Checkerboard Puzzles
Checkerboard (a.k.a. All Square Novelty Puzzle, Check-A-Board, ...) - 219
Sectional Checkerboard Puzzle - 220
Chequers (a.k.a. Famous Bug House Puzzle) - 225
The Bug House Puzzle - 227
Famous Baffling Checkerboard Puzzle - 228
XceL Checkerboard Puzzle No. 1 - 229
XceL Checkerboard Puzzle No. 2 - 230
Gyro Checker Board Jig Saw Puzzle - 231
Draught Board Puzzle (a.k.a. Krazee Checkerboard Puzzle, Zebas Puzzle,...) - 232
Adams Idiot's Delight Checkerboard Puzzle - 235
Japanese 19 Piece Checkerboard Puzzle - 236
Richter Tangram and the Other 36 Anchor Stone Puzzles
Anchor Puzzle Tangram (a.k.a Caricature, Cut-Up Square ... Richter No. 8) - 237
The Nine (a.k.a. All Nine, Richter No. 1) - 247
Lightning Conductor (a.k.a. Richter No. 2) - 249
Egg Of Columbus (a.k.a. Columbus' Egg, Columbian Puzzle, Richter No. 3) - 253
Patience Prover (a.k.a. Richter No. 4) - 256
Trouble Killer (a.k.a. Richter No. 5) - 259
Heart Puzzle (a.k.a. Richter No. 6) - 263
Kobold (a.k.a. Richter No. 7) - 269
Circular Puzzle (a.k.a. Richter No. 9) - 271
Cross Puzzle (a.k.a. Richter No. 10) - 274
Not Too Hasty (a.k.a. Richter No. 11) - 278
Pythagoras (a.k.a. Richter No. 12) - 281
Tormentor (a.k.a. Richter No. 13) - 287
BeQuiet (a.k.a. Richter No. 14 /3) - 292
Sphinx (a.k.a. Lott's Stone Puzzle, Richter No. 15 / 16) - 295
Magic Egg (a.k.a. Miracle Egg, Richter Anchor Stone Puzzle No. 16 / 17) - 299
Wrath Breaker (a.k.a. Richter No. 17) - 301
Richter Anchor Stone Puzzle No. 23 - 305
Richter Anchor Stone Puzzle No. 26 - 306
Richter Anchor Stone Puzzle No. 27 - 307
Richter Anchor Stone Puzzle No. 28 - 308
Richter Anchor Stone Puzzle No. 29 - 309
Richter Anchor Stone Puzzle No. 30 - 310
Richter Anchor Stone Puzzle No. 31 - 311
Richter Anchor Stone Puzzle No. 35 - 315
Richter Anchor Stone Puzzle No. 36 - 316
Richter Summary - 317
Some Other Richter Puzzles and Games
Richter Piccolo Nr. T1 (a.k.a. Richter Picco Nr. T1) - 325
Richter Hamleys - 326
Richter Trench and Zoo Puzzles (a.k.a. Schutzengraben, Zoologischer-Garten) - 327
Richter Star Puzzle - 330
Richter Puzzle Mosaic No. 3 - 333
Richter Meteor 1 - 334
Richter Meteor 6 - 335
Other Tangram-Like Puzzles
The Classic Tangram (a.k.a. Richter Anchor Puzzle) - 336
Daddling - 337
Pythagoras - 338
Voodoo - 339
HiHo - 340
Sherlock Holmes - 341
Scrambled Egg - 343
121 Puzzles - 344
ELZZUP - 345
PIC-TUR-ETT - 350
King Tut's Puzzle - 352
HIQU - 353
Shape By Shape - 354
Other 2D Puzzles With Polygonal Shapes
Four F's (a.k.a. F Puzzle) - 355
Four Piece Square (a.k.a. Magic Square) - 356
Double Square (a.k.a Square Me, Five Block Puzzle, Madagascar Madness) - 357
Red Circle Puzzle - 360
Missing T (a.k.a. T Puzzle, Magic T, Cut-Up T, Pa's T Puzzle, etc.) - 361
What's Your Score - 364
FPuzzle (theF) - 365
H Puzzle - 366
Pie Without E - 367
Make A Square - 368
Major War Problem - 369
Other 2D Packing Puzzles
Checking In - 370
Decoy Puzzle - 371
Batee Baseball - 372
Blockade - 373
Four T Puzzle - 374
Pencil Puzzle - 375
Pearl In The Shell - 376
Czech Farms - 377
Seven - 378
Pentominoes
Pentominoes (a.k.a Polyominoes) - 379
Twin Box Pentominoes - 387
3D Box Filling
Block Head (a.k.a. Sneaky Squares, Stark Raving Cubes, Square Fit, KUBI) - 388
Three Piece Block Head (a.k.a. The Third Degree) - 389
Coffin's 271A - 390
Log Stacker - 391
Dice Packing Box - 392
Chaotic Cube - 393
Pack It In - 396
Cube Root Blocks - 397
Parcel Post - 398
Bermuda Hexagon - 399
Matching - 400
2D Matching
Rubik's Tangle 3x3 (a.k.a Rubik's Mini Tangle) - 401
Rubik's Tangle 3x3 Double Sided - 402
Rubik's Tangle 5x5 - 403
Cluzzelei - 404
Crazy Puzzles - 405
McDonald Land Guzzle - 406
Infants Hospital - The Magic Line - 408
Krazee Links (a.k.a Endless Chain) - 409
Lost Rope - 410
Drive Ya Nuts - 411
Circus Seven (a.k.a. Mind Exerciser) - 412
Circus Puzzler (a.k.a. Color Matcher) - 413
Color Match - 414
Thinkominos - 415
Match The Colors - 416
Triazzle - 417
Bee - 418
Invisible - 419
Snake Pit - 420
Frog Pond - 421
Tool Trouble - 422
Transposer 6 & Bonbons - 423
Transposer Kaboozle - 424
Tantrix Discovery - 425
Tantrix Extreme - 426
Great Gears - 428
Spectra - 429
Instant Insanity Family
Instant Insanity (a.k.a Katzenjammer, Great Tantalizer, Face-4, ...) - 431
The Grand Army Puzzle - 444
The Allies Flag Puzzle (a.k.a. The Allied Flags Puzzle) - 445
The Allies Flags Puzzle - 446
Tantalizing Ten - 447
Cuss - 448
Iribako - 449
Drives You Crazy - 450
Boer War Puzzle - 451
Other 3D Matching
Bolygok - 453
Double Disaster - 454
Mental Blocks - 455
Disney Cubes - 456
Make A Dice (a.k.a. Spots Puzzle) - 457
Twice Dice - 458
Loony Tunes Blocks - 459
Smarts Pyramid - 460
Smarts PyramidJr - 461
The Rock - 462
Einstein Cube - 463
Rubik Triamid - 464
Other 3D Shape Assembly - 465
Convex Polyhedral Shapes
Two Piece Pyramid (a.k.a. Magic Pyramid) - 466
Three Piece Tetrahedron - 467
Four Piece Pyramid, Version 1 - 468
Four Piece Pyramid, Version 2 - 469
Four Piece Tetrahedron - 470
Truncated Tetrahedron - 471
Five Piece Tetrahedron - 472
Truncated Octahedra - 473
Truncated Cubes - 474
Garnet - 475
Y-Knot - 476
More Complex Polyhedral Shapes
Three Cubes Puzzle - 477
Three Piece Block - 478
Three Boxy - 479
Three Bunnies - 480
118-X - 481
Three Pairs - 482
Augmented Four Corners - 483
Turnabout - 484
Triumph - 485
Fusion Confusion - 486
Rosebud - 487
Twelve Piece Separation - 488
Crystal Pyramid - 491
3D Jigsaw Puzzles
Four Piece Jigsaw Puzzle - 492
Four Piece Jigsaw Cube - 493
Wonder Puzzle Block - 494
3x3 Chinese Zigzag - 495
3x4 Chinese Zigzag - 496
Wonders Of The World Cube Puzzle - 497
Jigsaw Dog - 498
Misc. Shape Assembly
Oskar's Matchboxes - 499
Pin-Hole Puzzle (a.k.a Pegged Puzzle) - 500
Wood Star - 501
Saturn Ring - 502
Rubik's Snake - 503
Yin And Yang - 504
Wooden-Do-It (a.k.a. Construction Cigar, Cigar Puzzle) - 505
Gumball Keychains - 510
Hartley's Humpty Dumpty - 511
Almost Impossible Heart - 512
Rubik's Cube Etc. - 513
Rubik's Cube - The Two That Started It All
Rubik's 2x2x2 Pocket Cube - 514
Rubik's 3x3x3 Cube - 525
More Rubik's Type Cubes
Rubik1x2x2 - 541
Rubik 1x2x3 - 542
Rubik 1x2x5 - 544
Rubik 1x2x9 - 545
Rubik 1x2x13 (a.k.a. Unlucky Twist) - 546
Rubik 1x3x3 Floppy Cube - 547
Rubik1x3x3 Floppy Mirror Cube (a.k.a. Magic Floppy Cube) - 548
Rubik1x3x3 Scramble Cube - 549
Rubik 2x2x2 Bandaged - 550
Rubik 2x2x2 Double Bandaged - 551
Rubik 2x2x2 Nested (a.k.a. Rubik 2x2x2 Super Square) - 552
Rubik 2x2x2 Cubes Fused - 553
Rubik 2x2x2 McDonalds - 554
Rubik 2x2x3 Tower Cube (a.k.a. Slim Tower, Franken Tower) - 555
Rubik 2x2x4 Tower - 556
Rubik 2x2x4 Nested (a.k.a. Rubik 2x2x4 Super Square) - 557
Rubik 2x2x23 (a.k.a. Overlap Cube) - 558
Rubik 2x3x3 Domino - 559
Rubik2x3x3 Layered - 560
Rubik 2x3x4 - 561
Rubik 2x4x4 (a.k.a. WitEden 2x4x4) - 562
Rubik's Color Blocks - 563
Rubik 3x3x3 Mirror Cube (a.k.a. Mirror Block, Yong Jun Cube) - 564
Rubik3x3x3 Fisher Cube (a.k.a. Square King) - 565
Rubik 3x3x3 Void Cube (a.k.a. Holey Cube) - 566
Rubik 3x3x3 Edges Only (a.k.a. Cornerless Void Cub) - 568
Rubik 3x3x3 Fourth Dimension - 569
Rubik 3x3x3 Scotland - 570
Rubik 3x3x3 Layered - 571
Rubik's 3x3x3 Perpetual Calendar - 572
Rubik 3x3x3 Bandaged (a.k.a. Bicube) - 573
Rubik 3x3x3 Patched (a.k.a. Fused Cube) - 574
Rubik 3x3x3 Brick (a.k.a Brick Cube) - 575
Rubik 3x3x3 Latch Cube - 576
Rubik 3x3x3 Constrained (a.k.a. TomZ / Tom's Constrained Cube) - 577
Rubik 3x3x3 Treasure Box - 578
Rubik 3x3x4 - 579
Rubik 3x3x5 - 580
Rubik 3x3x5 X - 581
Rubik 3x3x5 Cross - 582
Rubik 3x3x9 - 583
Rubik 3x3x9RoadBlock - 584
Rubik 3x4x5 - 585
Rubik 4x4x4 - 586
Rubik 4x4x4 Patched - 594
Rubik 4x4x4 Brick - 595
Rubik 4x4x5 - 596
Rubik 4x4x6 (a.k.a. TomZ 4x4x6 Cuboid) - 597
Rubik 5x5x5 - 598
Rubik 6x6x6 (a.k.a. V-Cube 6x6x6) - 601
Rubik 7x7x7 (a.k.a. V-Cube 7x7x7) - 602
Large Rubik Cubes - 603
Huge Rubik Cubes - 604
Camouflage Cubes / Evil Cuboids
Camouflage Cube 3x3x3 - 605
Camouflage Cube 3x4x4 - 606
Evil Cuboid 2x3x4 - 607
Evil Cuboid 3x3x3 - 608
Evil Cuboid 3x4x5 - 609
Crazy Cubes
Crazy Cube 2x3x3 - 610
Crazy Cube 3x3x3 - 611
Crazy Cube 3x3x7 (a.k.a. WitEden Super Magic Cube) - 612
Crazy Cube 4x4x4 - 613
Crazy Cube 4x4x4 Two - 614
Other Rectangular Shapes
Mixup Cube - 615
Ghost Cube - 616
Pocket Cube - 617
Axel Cube - 618
Skewb - 619
Holey Skewb (a.k.a. Void Skewb) - 621
Pitcher Insanity Cube - 622
Golden Cube - 623
Six Spots - 624
Dino Cube (a.k.a. Dinosaur Cube) - 625
Blue Magic (a.k.a. Black Flower Cube, Star Cube, Rex Cube) - 626
Mosaic Cube - 627
Square 1 (a.k.a. Super Cubix, Cube 21) - 628
Helicopter Cube - 636
Curvy Copter - 637
Geared Shapes
Geared 1x1x4 - 638
Geared 2x2x2 (a.k.a. David Gear Cube) - 639
Geared Mixup - 640
Gear Cube - 641
Gear Barrel - 642
Gear Cube Extreme - 643
Timur Gear Skewb - 644
Gear Shift - 645
Gear Pyraminx - 646
Gear Pyraminx2 (a.k.a. Gear Mastermorphix) - 647
Gear Minx - 648
Gear Change - 649
Gear Octahedron (a.k.a. Timur Gear Corner Turning Octahedron) - 650
Gear Ball - 651
Pyrmid and Diamond Shapes
Pyraminx - 652
Master Pyraminx - 657
Pyraminx Duo - 658
Pyraminx Diamond - 659
Jing's Pyraminx (a.k.a. Rounded Halpern-Meier Pyramid) - 660
Crazy Pyraminx (a.k.a. Crazy Tetrahedron Plus) - 661
Tetraminx - 662
Professor Pyraminx - 663
Vulcano - 664
Megaminx (a.k.a. Supernova) - 665
Holey Megaminx - 666
Crazy Megaminx - 667
Kilominx (a.k.a. Flowerminx) - 668
Master Kilominx - 669
Gigaminx - 670
Teraminx - 671
Pyraminx Crystal - 672
Helicopter Dodecahedron - 673
Skewb Diamond - 674
Super Skewb Diamond (a.k.a. Diamond Octahedron) - 675
Skewb Ultimate - 676
Skewb Kite - 677
Skewb Fourteen - 678
Pyrastar - 679
Pyramorphix (a.k.a Figurenmatch, Distortion Demon Square) - 680
Starburst (a.k.a. Star of David, Sterns Puzzle) - 681
Mastermorphix (a.k.a. Master Pyramorphinx) - 682
Dinomorphix - 683
Pillow Cube (a.k.a. Cushion Cube) - 684
Enhanced Pillow Cube (a.k.a. Polish Cushion) - 685
Confused Pillow Cube - 686
Hungarian Diamond - 687
Rhombi Diamond (a.k.a. Diamond Style Puzzler) - 688
Octahedron (a.k.a. Magic Octahedron) - 690
Full Octahedron - 691
Flowered Jewel (a.k.a Jewel Puzzler, Christopher's Magic Jewel, ...) - 692
Ghost Extreme - 693
Disc Shapes
Rubik's Cheese - 694
Rubik UFO - 695
UFO Cheese - 696
Rubik Cheese Cake - 697
Puck Puzzle (a.k.a Hockey Puck Puzzle) - 698
Saturn - 699
Hungarian UFO (a.k.a. Varia Disk) - 700
Tricky Disky (a.k.a. Tricky Disk, Mind Trapper) - 701
Smart Alex (a.k.a Alpa-2-Go) - 702
Netblock UFO / Sando Ring (a.k.a. King Ring) - 703
Octo (a.k.a. Meeting Colors, Disco Puzzle) - 704
Gerdig UFO - 705
Brain Ball - 706
Ball Shapes
Rubik 2x2x2 K-Ball - 707
Rubik 3x3x3 Ball - 708
Rubik 3x3x3 Apple - 709
Master Ball (a.k.a. Duo Master, Geo Master) - 710
Skewb Puzzle Ball (a.k.a Creative Puzzle Ball) - 713
Impossiball - 715
Dogic - 716
Misc Shapes
Rubik House (a.k.a. Eight Planets Bermuda Cube) - 717
Time Machine - 718
Rubik Barrel - 719
Cuboctahedron - 720
Rainbow Cube - 721
Rainbow Nautilus - 722
Pentahedron - 723
Pentahedron 5 Layer - 724
Crazy Pentahedron - 725
Dino Star - 727
Alexander's Star - 728
Platypus - 729
Skewb Egg (a.k.a. Golden Egg, Silver Egg, etc.) - 730
Brain Twist - 731
Roundy - 732
Other 3D Manipulation - 733
Panel Puzzles
Rubik Mini Magic Panels (a.k.a Rubik Magic Junior) - 734
Rubik's Magic Panels - 739
Rubik Magic Panels Create The Cube - 747
Rubik's Master Magic Panels - 749
Rubik Magic Cross Panels - 751
Rubik Super Magic Panels - 752
Towers Of Moving Balls Or Tiles
Whip-It Towers (a.k.a. Genius Puzzle) - 754
Varikon Towers - 755
Whip-It Ball - 757
Babylon Towers - 758
Calendar Bank - 759
Thai Tower (a.k.a. Clever Toys Tower) - 760
Numbers Barrel - 761
Missing Link - 762
Reduced Missing Link - 764
Extended Missing Link - 765
Doubled Missing Link - 766
Mini Missing Link - 768
Other Puzzles With Moving Balls or Tiles
Magic Rainbow Ball - 769
Hungarian Globe (a.k.a. Equator Ball, Magic Sphere, IQ Ball) - 770
Bolaris - 772
Magic Sphere - 773
Touchdown - 774
Twister (a.k.a. Wooden Screwball, Clever Toys Natural) - 775
Atomic Chaos (a.k.a. Kaos) - 776
Entrapment - 777
Pakovalec (a.k.a. Stupid Cylinder) - 778
Ten Billion Barrel (a.k.a. Billion Barrel, Tumbler Puzzle) - 779
Russian Revolver (a.k.a. Russian UFO, Soviet UFO, Russian Flower, Festival Flower) - 780
Back Spin (a.k.a. Loophole) - 782
Sliding Piece Can Puzzle - 783
Sliding Piece Can Puzzle - 784
Brain Racker - 785
The Orb (a.k.a. Orb-It, l'ORBS) - 786
Rubik's Shells - 787
Astrolabacus - 788
Movement of Pieces by Tilting or Pushing
Varikon Box 2x2x2 - 789
Varikon Box 3x3x3 - 790
Inversion - 791
Peter's Black Hole / Vadasz Cage (a.k.a. Inside Out, Magic Jack, IQ Cube) - 793
Mad Marbles - 794
Dice Box - 795
Clark's Cube - 796
Pionir Box (a.k.a. Pionir Cube) - 797
Rubik Dice - 798
Movement of Discs and Rings
Towers Of Hanoi (a.k.a. Pyramid Piling Puzzle, Rainbow Puzzle, Brahma Puzzle) - 799
Chinese Rings (a.k.a. Cardan's Rings, Baguenaudier) - 802
Spinout - 806
Hexadecimal Puzzle - 807
WanderRings - 811
Panex - 813
Manipulation Of Positioned Balls, Levers, Buttons, Etc.
Cmetrick - 814
Cmetrick Too (Hard) - 815
Planets - 816
SaturnLD - 817
Orbik - 820
Rolling Cubes - 821
Cross Teaser - 822
Rubik's Clock - 823
Cerebral Rings Puzzler - 825
Simultaneous Maze - 826
Misc.
Wisdom Ball (a.k.a. Mind Twister) - 827
SpongeBob PuzzlePants (a.k.a. SpongeBob Cube) - 828
Flip Side - 829
Kabalabda - 830
Rubik's Rabbits (a.k.a. Rubik's Hat) - 831
Enigma - 832
Brain Puzzler - 833
Sliding Pieces and Other 2D Manipulation - 834
Square Pieces
Fifteen Puzzle (4x4 squares, 15 tiles) - 835
RO-LET (4x4 squares, 15 tiles) - 884
Unocando (4x4 squares, 15 tiles) - 885
Missionary Puzzle (4x4 squares, 16 tiles) - 886
Sixteen Puzzle (4x4 + 1 squares, 16 tiles, a.k.a. Flintstones, Escher) - 887
Moving Day (2x3 squares, 5 tiles, a.k.a. 5-Block Puzzle, Lodging House Difficulty) - 888
Eight Puzzle (2x4 squares, 7 tiles, a.k.a Super Solitaire) - 889
Nine Puzzle (3x3 squares, 8 tiles, a.k.a. Superman, Tweety, Simpsons, etc.) - 890
Mystic (3x3 squares, 7 tiles) - 895
Magic Square 3x3 (3x3 squares, 9 tiles) - 896
Great Fifty Puzzle (4x4 squares, 16 tiles, a.k.a Magic Square 4x4) - 897
Panama Canal Puzzle (2x6 squares, 11 tiles) - 898
Bull's-Eye (3x4 squares, 11 tiles, a.k.a. Bullseye, Target, Zot) - 902
Good Luck (4x3 squares, 11 tiles) - 908
Ditho (3x5 squares, 14 tiles) - 909
Twenty (3x7 squares, 20 tiles - 912
Double Trouble Puzzle (5x5 squares, 24 tiles) - 913
Twenty Seven (4x7 squares, 27 tiles) - 914
Scrabble Pocket Puzzle (4x7 squares, 27 tiles) - 916
Cornell Crossword Puzzle (4x7 squares, 28 tiles) - 917
Thirty One (4x8 squares, 31 tiles, a.k.a. Jumble, TWIDL) - 918
Frog (4x8 squares, 31 tiles) - 919
Maps (4x8 squares, 31 tiles) - 920
SKOR (4x8 squares, 31 tiles) - 921
ScribeO (4x8 tiles, 31 tiles) - 922
Octopix (4x8 squares, 31 tiles) - 923
Forty Nine (7x7 squares, 48 tiles - 924
LINGO (4x14 squares, 55 tiles) - 925
Square Pieces With Obstacles
Grandpa's Car (a.k.a. Slide-Blocked Sliding Block) - 929
Time Puzzle - 930
Work Or Golf (a.k.a. Motor Garage Puzzle, Parka Car, Sputnik, E Peg Puzzle) - 933
Honor And Glory (a.k.a. Black And White) - 936
One Fish Another Fish - 938
Russian Rows - 939
Nite and Day(s) (a.k.a. Ride or Walk) - 940
Ride or Walk (a.k.a. Nite and Days) - 941
1234 Puzzle (a.k.a. Nite and Days, Ride or Walk) - 942
Fish or Dive - 943
Work or Golf Abridged - 944
1x2 Pieces and (in most cases) 1x1 pieces
Get My Goat (a.k.a. Kapture The Kron Prinz, Boogie Man, Center Point, ...) - 945
Line Up The Quinties - 951
Johnson City Puzzle - 953
Four Suits 2 - 955
Puzzle Contrast - 956
Sliding Arrow Through The Bottle Puzzle - 957
Slidem WWII Puzzles - 958
Monarch - 962
Sliding Chess Mate 36 - 963
Straight Arrow - 964
Dad's Puzzler Family - 4x5 Trays and Multiple Shapes Rectangular Pieces
Dad's Puzzler (a.k.a. Moving Puzzle, Tit-Bits Teaser 1, Pennant Puzzle, ...) - 965
Dads Puzzler - Humdinger Version - 1001
Dad's Puzzler - Exchange Version / Infants' Hospital - 1008
Quzzle And Quzzle Killer - 1015
Nine Block - 1019
Red Donkey, with Simple TJ, Century, Super Century (a.k.a. L'Ane Rouge, ...) - 1022
Traffic Jam / Let Me Through - 1032
Century Puzzles - 1037
Grand Master With Little House - 1043
Ushi And Ushi-Flipped - 1046
Hole In One With Royal Out and King Out - 1049
Fence The Cow - 1052
Dad's Puzzle Family Set With Fujiwara 15/22/25 and Super Compo - 1054
Dad's Puzzler Family With Obstacles and Non-Rectangular Pieces
D209 - 1059
Super Dries - 1060
Beyond Dad's Puzzler Family
Sunbeams Rainbow Puzzle - 1061
Infants Hospital Puzzle (a.k.a. Infants Progress Puzzle) - 1062
Trans-Atlantic (a.k.a. Ten Block Puzzle, Traffic Cop Tangle) - 1064
Happy Couple (with Ten Block and The Hughes Puzzle) - 1066
Flying Puzzle (a.k.a. Starry Puzzler, Tit-Bits Teaser No. 2, Ching Foo, ...) - 1072
Technocracy - 1082
George Washington Puzzle - 1083
Presidential Puzzle - 1086
Tit Bits Teaser No. 5 - 1088
Century Of Progress (a.k.a. South Pole Expedition) - 1093
Sliding Block Puzzle (a.k.a. Fifteen Block Puzzle, 1-2-3 Puzzle, ...) - 1095
Slide A While & Model Garage - 1100
Tokyo Parking / Rush Hour - 1105
Moota-Kun - 1109
Pink and Blue - 1111
Adam & Eve (a.k.a. Comic Scramble Game) - 1114
RunAway II - 1116
Neo Pink And Blue - 1118
Further Beyond Dad's Puzzler Family - Non-Rectangular Shapes
Ma's Puzzle (a.k.a. Spirit of '76, Wooden Puzzle, Rectangle Puzzle) - 1122
Dad's and Ma's Stumbling Blocks (a.k.a. Dad's Puzzler + Ma's Puzzle) - 1129
Mini Ma - 1130
Traffic Jam Puzzle (a.k.a. Tit-Bits Teaser No. 4) - 1131
Naoyuki Iwase 2012 - 1138
Naoyuki Iwase 2014 - 1140
Triple Tango - 1142
Clouds And Sheep - 1143
Slider (a.k.a. Hole In One, Idol Plays Slide Puzzle) - 1144
Heart-In - 1145
Soap - 1146
Block Ten (a.k.a. Apple) - 1147
Climb 15 - 1153
Stumbling Block - 1159
I Want You - 1161
Neo Black And White - 1163
Just Six Pieces - 1168
Solo - 1169
Solo Another - 1170
Angel And Satan - 1171
Kuroko And Dairu - 1172
Windmill - 1173
Two Sliding Squares - 1176
Sliding Pieces Non-Standard Movement - Multiple Layers
Fence the Sheep - 1177
Two Butterflies - 1181
Moon and Star - 1182
Get My Sheep - 1189
Two Eggs - 1191
Sliding Cross - 1201
Football Match - 1210
Sliding Pieces Non-Standard Movement - Rotations and Turntables
Egg (a.k.a. Dinosaur Egg, Dragon's Egg, Solo 2) - 1213
Enjoy Life - 1220
Dustin Puzzle - 1229
Easy - 1232
Easy 1989 - 1234
Sliding Pieces Non-Standard Movement - Capture Movement
Shuttle Five - 1236
Shuttle 1234 - 1238
Shuttle 123 - 1239
Sliding Eight 2 (Sliding Eight II) - 1240
Shimokita - 1242
H-Slider - 1250
My Towers of Hanoi - 1252
Sliding Three - 1259
Sliding Three Square - 1265
Neo Slide-9 - 1270
RunAway - 1272
Easy Trap - 1274
Trap - 1277
Tricky - 1286
Dog and Cat - 1294
My Dog - 1297
Two Dogs - 1299
Stacking Cups - 1302
Train Puzzle - 1305
Sliding Pieces Non-Standard Movement - Miscellaneous
African Mask - 1306
Who's The Boss - 1314
Fusion - 1320
Movement of Buttons, Balls, Numbers, etc.
New Fifteen Puzzle - 1321
Perplexity Puzzles (Perplexity, Automobile, This is Jonah, Panama Canal) - 1322
One To Ten - 1323
Good Luck Railroad Puzzle Game - 1324
Rotos - 1325
Puzzler Novice / Challenge / Avenger (a.k.a. Turnstile, Twinspin, ...) - 1326
Rotascope (a.k.a. Taquinoscope) - 1327
Rashkey - 1329
Hungarian Rings - 1330
Hungarian Rings Triple - 1331
Hungarian Rings Quad - 1332
Hungarian Olympic Rings - 1333
One Circle Two Circles - 1334
Billiards - 1335
Billiards 9-Ball - 1336
Flower - 1337
Trio - 1338
Trio 2 - 1339
Butterfly - 1340
Subway Shuffle - 1341
Movement of Tokens
Eight Peg Puzzle - 1347
TeeZ / Brain Buster - 1348
Peg Puzzle - 1349
Hopper (a.k.a. Downsize) - 1350
Mechanically Assisted Sliding Pieces
Top Spin / No. Crunch - 1352
Turnstyle (a.k.a. Tom's Turnstile) - 1353
Line Art - 1358
Colour Match - 1359
Magic Cross (a.k.a. Zauberkreuz) - 1360
Rubik's XV (a.k.a. Rubik's Fifteen) - 1361
Tsukuda's Square (a.k.a. It, 4x4 Four By Four Puzzle) - 1362
Uriblock (a.k.a. Mix Box) - 1363
Trillion - 1364
Port To Port And Triple Cross - 1366
Switch Back - 1370
SwissMad - 1371
Modern Times - 1372
Mad Triad Challenge (Twisting Tri-Side Puzzle) - 1373
Mad Triad Handy (Twisting Tri-Side Puzzle) - 1374
La Cerradura Doble - 1375
Elemental Neon - 1376
Fluorine - 1378
SF PP STAR 29 - 1379
String and Wire Puzzles - 1380
Move or Remove a Ring
Horse Shoes - 1381
Ball And Ring (a.k.a. Ball And Chain) - 1382
Moving Rings (a.k.a. Moving Beads, Tiger Cross, Wizzard Wedding Ring) - 1383
Wits End - 1384
Single Loop Wit's End - 1386
Loop Trap - 1387
Parallel Dimension - 1388
Disengage Two Pieces
Nails - 1389
Wire U's - 1390
Wire P's - 1391
Wire Heart - 1392
Cast Loop - 1393
Cast Ring - 1394
Vortex - 1395
Simple Knot 47091 - 1396
EZ Atom 47092 - 1397
Lucky Clover - 1398
Misc.
Rod and Loop - 1399
Hide The Knots - 1400
Beer Bottle Puzzle - 1401
Other Puzzles - 1402
Mechanicl Challenges
TakitaparT (a.k.a Take It Apart) - 1403
Double Puzzle - 1404
Rook Puzzle - 1405
Bolt And Ball - 1406
Spark Plug Puzzle (a.k.a. Bougie, Get Charged) - 1407
Cage Puzzle - 1408
Nut Case - 1409
Drive The USA - 1410
Screwball - 1411
Dexterity Puzzles
Abercrombie & Fitch Dexterity Puzzles - 1412
A Ward In The Infant's Hospital (a.k.a. The Little Patients Puzzle) - 1413
ElsieCow - 1414
Reiss Style 393 - 1415
Crazy Maze - 1416
Metro - 1417
Perplexus - 1418
Puzzle Boxes
Parrot Box - 1419
Spin Box - 1420
Coffin's Double Play X-48 - 1421
Stickman Grandfather Clock - 1422
Stickman Oak Wood Slide Box - 1428
Stickman Fulcrum Box - 1434
Pirate's Wallet Box (a.k.a. Stickman No. 27) - 1435
Stickman Burr Tile Box - 1444
CruciBox - 1451
Misc
Jigsaw Heart - 1453
Infants Hospital Jigsaw Puzzle - 1454
Magic Chalice - 1455
What's Your Age - 1456
The Amazing Dr. Nim - 1457
Games - 1467
Goblet - 1468
Quixo - 1471
Quarto - 1472
Othello - 1473
Nine Mens Morris (a.k.a. Mill, Muhle, Merelles / Merilles, Mulino) - 1474
Tablut - 1476
Senet - 1478
Nannon (a.k.a. Nano Backgammon) - 1482
Make Numbers - 1483
Write a Self-Printing Program - 1484
Books - 1486
Hoffmann Related Books
Hoffmann's Puzzles Old and New (1893) - 1487
Hordern's Edition Of The Hoffmann Book (1993) - 1493
Het Puzzle-Boek (1900) - 1495
Hoffmann Posthumous Books (1925) - 1496
Hoffmann's Best Math Book (2007) - 1497
Hoffmann Patience Games Book (1892) - 1498
Hoffmann's Magic Trilogy Books (1920) - 1499
Hoffmann Study Book (1977) - 1500
Other Books from Before 1960
Robert Merry's Books Of Puzzles 1-3 (1866) - 1501
Excursions Into Puzzledom (1879) - 1503
Everybody's Puzzle Book (1890) - 1504
Richter Company U.S. Brochure (early 1900's) - 1505
New Book Of 200 Puzzles (1908) - 1512
Dudeney Books (1920's) - 1513
Dudeney Posthumous Books - 1514
Sam Loyd's Cyclopedia Of Puzzles (1914) - 1515
Sam Loyd and His Puzzles (1928) - 1516
Wyatt's 1928 and 1946 Books - 1517
Johnson Smith Catalog (reprinted from 1929) - 1518
Hirschberg Book (1930) - 1519
I-X-L Puzzle Book (1938) - 1520
Filipiak Book (1942) - 1521
Everythings A Puzzle (1953) - 1522
Books 1960 - 1999
Bell's History of Board Games (1960) - 1523
Murray's History of Board Games (1978) - 1524
Delft And Botermans Book (1978) - 1525
Winning Ways Books (1982) - 1526
Hordern's Sliding Puzzle Book (1986) - 1527
Slocum and Botermans Books (1986) - 1528
Cutler's 6-Piece Burr Books (1986) - 1529
The Mathematics Of Games (1989) - 1530
Coffin's Book On Polyhedral Dissections (1990) - 1531
Coffin's Puzzle Craft Books (1992) - 1532
The Puzzle Archade (1996) - 1533
Gabarchuk's Sliding Block Puzzle Book (1996) - 1534
Frederickson's Dissections Book (1997) - 1535
G4G Tributes To Martin Gardner (1999) - 1536
Books 2000 - 2020
The Follette Puzzle Design Book (2001) - 1537
Frederickson Books (2002, 2006, 2017) - 1538
The Tangram Book (2003) - 1539
Haubrich's Checkerboard Puzzles (2005) - 1540
The Fifteen Book (2006) - 1541
A Visual History of The S.S. Adams Co. (2006) - 1542
The Self and Lensch Puzzle Design Book (2006) - 1543
Boardman's Puzzle Projects Book (2007) - 1544
The Cube Book (2009) - 1545
Hess Mathlete Book (2009) - 1546
Diaconis and Graham Book (2012) - 1547
Stickman Book (2012) - 1548
The Anchor Puzzle Book (2012) - 1550
Coffin's AP-ART Book (2014) - 1552
Books after 2020 - save a tree and go paperless!

Pieces are formed by removing unit cubes from rectilinear solid pieces. A burr is notchable if it can be made with just straight cuts. Some burrs have a "key" piece that slides out. More complex ones have a number of internal voids (called holes), where removing the first piece may require sliding several pieces. An assembly of a burr is a solved shape. An assembly is a solution if it can be achieved by starting with the pieces apart and making legal moves. The level of a solution is the minimum number of moves required to remove the first piece (or separate the puzzle into two parts). The level of a burr is the lowest level of its solutions. Note that to compute level, we use Cutler's definition, where the movement of several pieces together, or the consecutive movement of pieces in the same direction, counts as a single "move". Burr level can be expressed with more than one number; e.g., 3.7.2 means 3 moves to remove the first piece, 7 moves to remove the second piece, and 2 moves to remove the third piece.
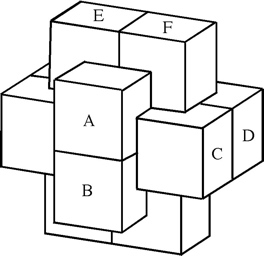
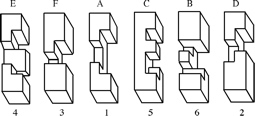
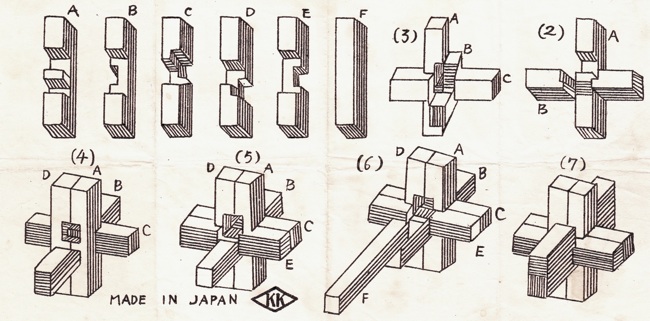
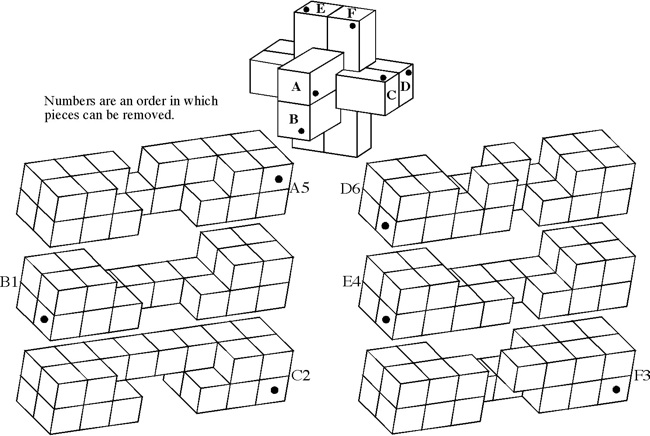
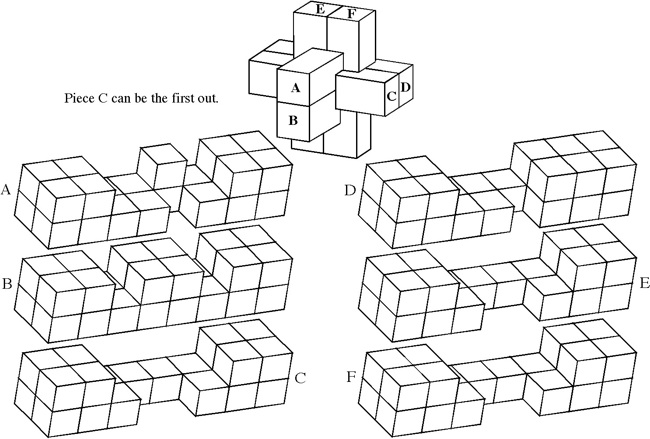
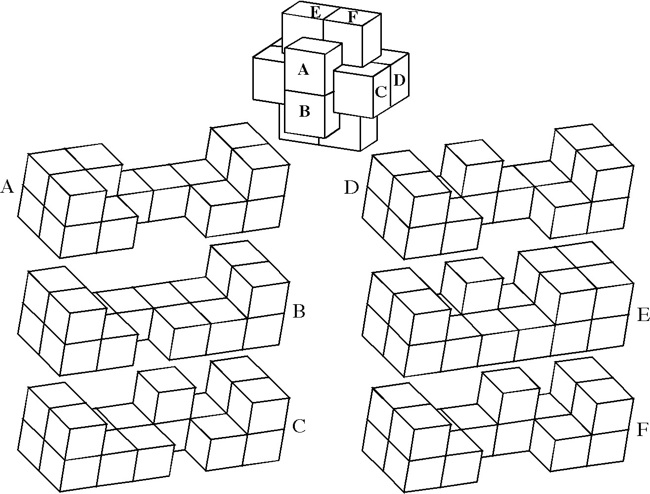
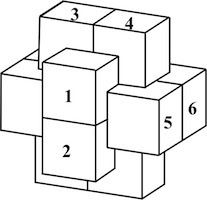
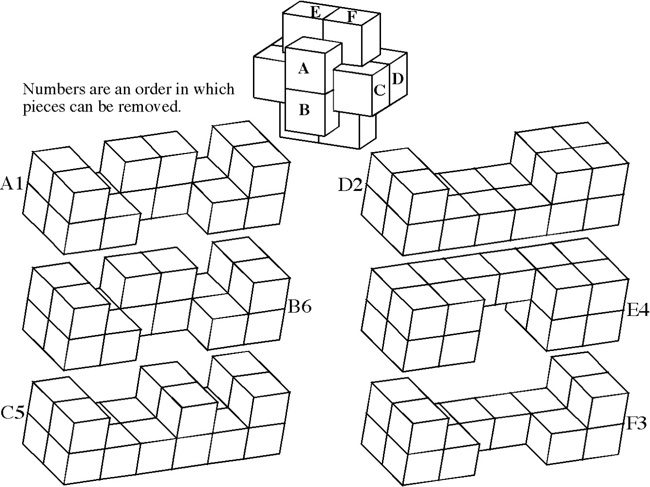
The most well known burr is the standard 6 piece burr, with 2 x 2 x 6 unit pieces (or sometimes 2 x 2 x 8). For example, the figure above shows Coffin's Improved Burr, which requires 3 moves to remove the first piece (letters show how pieces fit, numbers indicate an order in which they can be disassembled).
The number of holes in a standard 6-piece burr:Standard 6-piece burr records, from the computer work of Bill Cutler:
- Volume of six solid pieces = 6 x 24 = 144 (or 192 for 2x2x8 pieces).
- Volume of a solid burr = 24+24+16+16+12+12 = 104 (or 152 for 2x2x8 pieces).
- Volume difference = 40.
- Holes = (total number of unit cubes removed from the six pieces) - 40.
- Highest level for unique solution with 3 holes = 7.
- Highest level for unique solution with 4 holes = 8.
- Highest level for unique solution with 5 holes = 9.
- Highest level with a unique solution (uses 7 holes) = 10.
- There are no standard 6-piece burrs of level 11.
- Highest possible level (its the only one, but has non-unique solution) = 12.
- Highest level for unique notchable (has 7 holes) = 5.
- Highest level for notchable with non-unique solution = 10.
• Fractional or rotation moves.
• Non-rectangular cuts.
• Solutions with exposed holes.
• Ball bearing(s) inside that may have to move during solving.
• Additional moves to remove the second piece require more moves than the first.
Non-standard 6-piece burrs have six pieces but don't adhere to standard construction rules. Burrs in the theme of the standard 6-piece burrs but with more pieces can be difficult, especially when combined with non-standard constructions. Burrs with as few as 3 pieces can also be quite difficult (e.g., the Cuter Level 8 GigaBurr). Three piece "knots" fit together in a simple but non-obvious way. Some three piece burrs require unusual twists or diagonal motions.
The basic idea of a burr is quite old. The 1893 Hoffman book presents a wood knot as "Cross Keys" and a 6-piece burr as "The Nut". The Slocum and Botermans New Book of Puzzles, on page 52 discusses the Spears Puzzle knots manufactured in Bavaria in 1910 and marketed in England; it is also mentioned that six piece burrs appeared in Bestelmeier's 1803 Toy Catalog. The 1929 Johnson and Smith Catalog, on pages 254-255, shows a 6-piece burr, a two burr stick, and related wood puzzles. The Puzzlers' Tribute book, on page 260 cites a 6-piece burr called the Devil's Hoof and a 24-piece burr called the Large Devil's Hoof in a Catel's catalogue of 1785, and credits David Singmaster's example of a 6-piece burr in a 1733 Spanish book by Pablo Minguet E. Irol; also, on page 262 it credits the Mikado Puzzle as shown in the 1915 C. J. Felsman Catalogue:

The 1942 Filipiak book has a substantial discussion of burr puzzles; here are figures it shows of a 3-piece wooden knot, a 6-piece burr, and a 6-piece burr set:
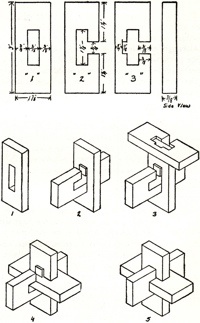
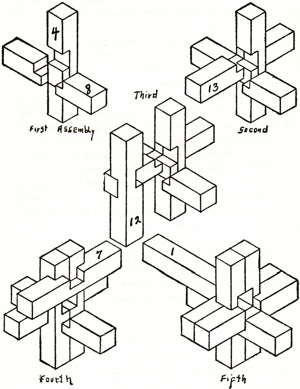
There have been many burr patents; for example, here are the figures from the 1890 Altekruse and 1917 Brown patents:
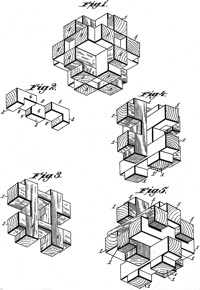
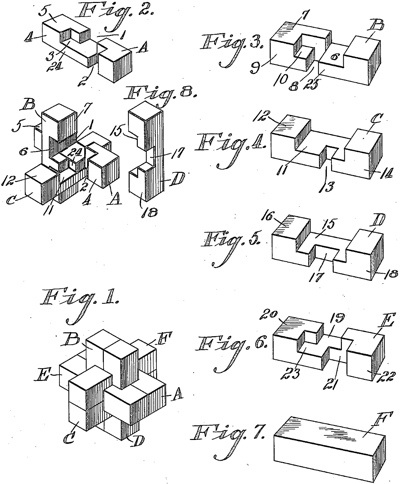
Chandler Patent, from: www.uspto.gov - patent no. 393,816
Altekruse Patent, from: www.uspto.gov - patent no. 430,502
Porter Patent, from: www.uspto.gov - patent no. 524,212
Nelson Patent, from: www.uspto.gov - patent no. 588,705
Ford Patent, from: www.uspto.gov - patent no. 779,121
Curtis Patent, from: www.uspto.gov - patent no. 781,050
Erickson Patent, from: www.uspto.gov - patent no. 985,253
Banic Patent, from: www.uspto.gov - patent no. 1,099,159
Brown Patent, from: www.uspto.gov - patent no. 1,225,760
Keiser Patent, from: www.uspto.gov - patent no. 1,261,242
Senyk Patent, from: www.uspto.gov - patent no. 1,350,039
Schenk Patent, from: www.uspto.gov - patent no. 1,455,009
Kramariuk Patent, from: www.uspto.gov - patent no. 1,542,148
Turner Patent, from: www.uspto.gov - patent no. 2,836,421
Pidgeon Patent, from: www.uspto.gov - patent no. 4,148,489
Derouin Patent, from: www.uspto.gov - patent no. 4,880,238
Dykstra Patent, from: www.uspto.gov - patent no. 5,040,797
Rob's Puzzle Page, from: http://home.comcast.net/~stegmann/interlocking.htm
Cutler's Holey 6PB Booklet, from: http://home.comcast.net/~billcutler/docs/H6PB/index.html
Cutler's Computer Analysis, from: http://home.comcast.net/~billcutler/docs/CA6PB/index.html
IBM Burr Page (edited), from: http://www.research.ibm.com/BurrPuzzles
Curfs' Page, from: http://home.tiscali.nl/~bcurfs/homepage/burrs/burrs-e.htm
Math Games Page, from: http://www.maa.org/editorial/mathgames/mathgames_08_02_04.html
Wikipedia Burr Page, from: http://en.wikipedia.org/wiki/Burr_puzzle
Mathematische Basteleien Page, from: http://www.mathematische-basteleien.de/devilsknot.htm
Mr. Puzzle Page, from: http://www.mrpuzzle.com.au/category129_1.htm
Source Forge Page, from: http://burrtools.sourceforge.net/gui-doc/BurrDesignTools.html

Interlocking Puzzles,
circa 2000.
(3 wood pieces, 2.75")
Daniel C. Alsmeyer 2006,
Sabriday Puzzles.
(3 wood pieces, 3")
"Triple Cross",
Puzzles & BT 2006.
(3 wood pieces, 3.2")
Three examples of the wood knot that was patented by M. P. Rao in 1980. Here are the directions that were sold with the Sabriday version:
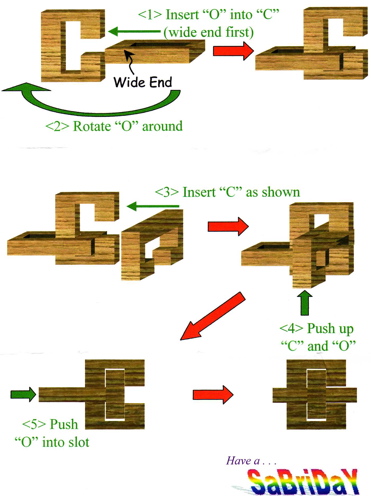
Further reading:
Rao Patent, from: www.uspto.gov - patent no. 4,198,053


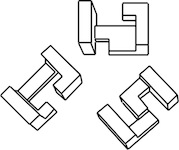
Designed by Kouki Kusumi, Made by Eric Fuller 2022.
(Zebrawood, Wenge, and Maple, each piece 3" x 1.75" x 1/2")
Three identical pieces make a more difficult puzzle than a traditional Wood Knot. Each piece has a groove on its long edge and a pin on the inside. The pins slide nicely in the grooves and it is natural to assume that the solved puzzle has all three pins in a groove. The key to solving is that only 2 of the three pins end up in a groove, where the third pin ends up in a piece gap.
Begin with the pieces in their solution orientation as shown in the first photo below (the left piece pin is at the bottom, the middle piece pin is at the back, and the right piece pin is at the right). Then sliding the pieces together comes naturally:







a.k.a. Three Piece Puzzle
Purchesed from Puzzles and Brain teasers Ebay Store 2006.
(three wood pieces, 3.75 inches;
described on pages 106 and 139 of the 1983 Hoffmann book)

Designed and made by Interlocking Puzzles, circa 2000.
(walnut, paduk, and hard maple, 3 inches square)
Unlike the common three piece wood knot, there are no identical pieces:


Designed by Oskar Van Deventer, purchased from Bits And Pieces, 2008.
(metal, 1.4 inches)
Here are photographs of the three pieces being disassembled:




Here is the solution sheet that was sold with the puzzle:

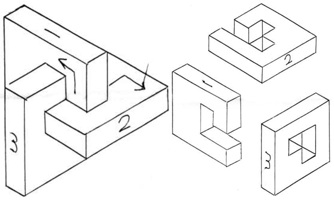
Designed by Oskar van Deventer 1983.
Made by Tom Lensch.
Sold by Cubic Dissection 2005.
(three wood pieces and solution figures, 3 inches)

Designed by Ronald Kint-Bruynseels, made by Eric Fuller 2006, Level 8.
(wood, 3 inches)
Here are the 8 assembly steps:










Designed by Wilhelm Segerblom in the late 1800's.
(three wood pieces, 2.25 inches)
The IBM Burr page cites the April 1899 issue of Scientific American as publishing this puzzle. Three identical pieces each have outer dimensions 2 by 2 by 6 units. Each has all of the center 2 by 2 by 2 portion removed except for a 1 by 1 by 2 rod that is beveled at 45 degrees (a total of 7 units of wood has been removed from each piece). To assemble, all three pieces have to be slid together simultaneously (an outside surface of the rod slides perpendicular to one piece while the beveled surface slides over the corner of another). It is not possible to put two pieces together and then slide the third one in. The figure below shows the three identical pieces in the orientation to be put together.

Further reading:
IBM Burr Page, from: http://www.research.ibm.com/BurrPuzzles/


Designed by R. Stanton, made by E. Fuller 2008.
(Curly Maple, 3 inches)
Three identical piece slide together simultaneously to make a 3-dimensional cross.
Assembly: Hold one piece vertically and determine how a second piece fits (there are only a few possibilities; look for the one where two faces sit nicely together), then carefully slide it out and put that piece down on the table without disturbing its orientation, then do the same for the third piece. Now that you have determined the orientation of the three pieces, hold them in their orientations so that they are just on the verge of engaging, line everything up, and then just squeeze the three together.
Disassembly: Randomly jiggle and push on the pieces until you can get it to come apart just a bit. You can keep doing this until the puzzle comes apart, but as it comes apart a bit you should be able to find the right way to hold on to and push two of the pieces so that the puzzle slides apart, and you can just push and pull to make it expand and contract, where the third piece is being controlled by the movement of the other two that you are holding.
Here are two views of the puzzle in a partially expanded state:



Designed by Dic Sonneveld, made by Tom Lensch, circa 1990.
(Walnut, 2.25 inches)
Three identical pieces come apart in simultaneous motion:



Designed by Jim Gooch,
made by Eric Fuller,
purchased from www.cubicdissection.com.
(three wood pieces, 2.9 inches)
At first this appears to be a three piece burr made with excess play in the fit. However, the extra play is just enough so that these three identical pieces come apart with a non-rectilinear movement.


Designed by J. Krijnen, made by E. Fuller 2008, unique level 7.
(Quilted Sapelle, 3 inches)
Here are steps ito dissassemble:








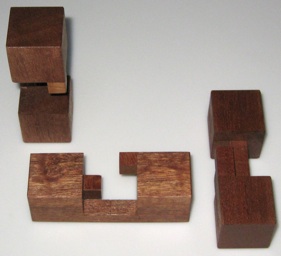


Designed by Noah Prettyman, made by Eric Fuller 2018, level 8.
(Zebrawood, 3 inches square)
The pieces are precisely made, while the puzzle overall is very loose (where in only in some positions can it be stood up without a piece sliding down). Here is what the puzzle maker said:"Just Three is from the brilliant mind of young prodigy Noah Prettyman. The level 8.4 solution is quite tricky for an interlocking burr with only three pieces. Beautifully crafted from milled zebrawood and maple, this puzzle looks great when solved! Construction is very precise, with a bit of room left for humidity expansion as it's very dry in the workshop this time of year."Here are six positions in an assembly; note that for the final photo, the left-to-right piece has been offset slightly so that it does not (by gravity) slide down a unit distance:








Designed by O. Yamamoto, made E. Fuller 2008, unique level 4 with a twist.
(Walnut, 3 inches)
Here are steps ito dissassemble (there are two photos for the second step, which is a twist):







Designed by T. Jolly, made by E. Fuller and sold by Cubic Dissection 2008, level 6.
(Bloodwood, Wenge, Holly, 3 inches)
When assembled, one can look through the center holes in any of the three directions. Here are photographs of the six steps to disassemble, where step 2 is a twist:








Designed by Bill Cutler 1999, made by Jerry McFarland, level 8.
(left: GigaBurr -Walnut, 2.2 inches; right: GigaBurr II - Cherry, 2.2 inches)
The 250 billion puzzles of this type were enumerated with a computer by Bill Cutler. The highest level (moves to remove the first piece) was 8, of which there were 80 different puzzles, where only 3 had only 9 internal voids. Two of these are the GigaBurr and GigaBurr II, and the third is a symmetric version of the GigaBurr II. To solve, two pieces can go together only one way, and then visualize the third piece in its final position to determine how to get it in and out. Here are photos of solving (the third sequence shows the symmetric GigaBurr-2 made by someone else):














Designed and made by Bill Cutler and Jerry McFarland 2001, level 6.
(left: Poplar / Walnut, 2.2 inches;
right: Cherry / Walnut / Wenge, 2.2 inches)
The basic design of the 3-piece GigaBurr and GigaBurr-2 was expanded to a 5x5x5 cube by gluing on edge and corner pieces. Cutler's computer search yielded three basic level 6 puzzles, of which these are two.

Designed by Bill Cutler.
(Walnut, 3.5 inches)
Four irregular shaped pieces and two ball bearings, which when assembled, look like a 6-piece burr. Falls apart easily.

Designed by William Hu, made by Eric Fuller, 2014.
(4 pieces, White Oak, Chakte Viga, 2" x 2" x 3")
This is what the puzzler maker says about the puzzle:"This seemingly simple puzzle uses a very interesting and difficult type of rotation. Ultra tricky and not like anything I've tried before. Level nine and fun...watch out, this one will have you pulling your hair out! Construction was tricky...the solid side spine and endgrain key pieces were fun to make, but very labor intensive. Fit is excellent; may be difficult to solve in highly humid environments due to the very close tolerances involved."At first it looks like there is no way for it to come apart. If we number the pieces 1, 2, 3, 4 going from left to right, the trick to dissassembly is to tilt piece three and rotate piece two 90 degrees (clockwise as you look through the puzzle from left to right). The puzzle generally has a nice loose fit, but it is a tight fit at the point of the rotation.









Designed by Emil Askerli, made by Eric Fuller 2016.
(5 pieces, Cherry & Walnut, 2+5/8 inches square)
In the photo above, the dark piece is not a single piece; the front portion is attached to the top right and the back portion is attached to the top left. Here is what the puzzle maker said:"I had already chosen the puzzles for the next update when Emil posted the Disguised and Camouflaged burr designs. I immediately contacted him for permission and squeezed them into the schedule because I thought the idea was so unique. Take a regular six piece burr but chop a piece or two in half and secure them. BOOM, now you have a traditional looking six piece burr puzzle that behaves very differently than usual. I used contrasting woods to give a visual hint of the unusual nature of these two. Disguised Burr has a level 7.2.2 solution. Construction of this puzzle is our usuall burr quality (outstanding!) with milled pieces and a precise yet accommodating fit."

Designed by Jim Gooch, made by Eric Fuller, level 9.
(Pau Amerillo / Wenge / Bocote, 3 inches)
The pieces consist of a "block", two identical "rods" in symmetric orientations, and two identical "plates" in symmetric orientations. Orientate the puzzle as shown on the left below (the right rod will drop down as shown if the puzzle is not too tight), exchange the plates by passing them through each other, then the right plate (which was the left plate) can be twisted (in two ways) and removed (or without twisting it can be slid out together with the right rod).



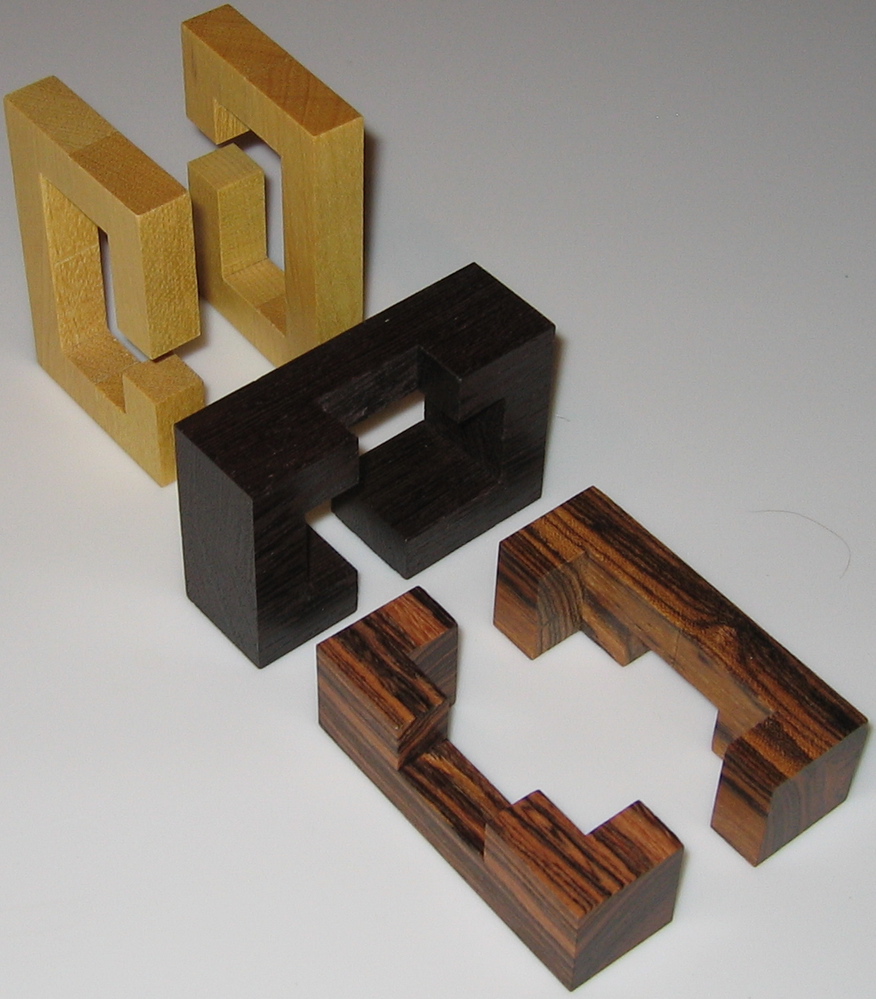

Designed by Tim Alkema, made by Eric Fuller 2017.
(5 pieces, Granadillo & Ash, 2+9/16 inches square)
Here is what the puzzle maker said:"Rift is such a simple design it's elegant. Three burr pieces and a two piece cage that dances around the assembly. The moves are so unconventional that the level 8 solution is tougher than you would expect. Disassembly has a trick to it as well. This is an excellent puzzle, I'm glad I made it, and I'm looking forward to its big brother "Schism" in the next update. Construction of this puzzle is excellent. Fit is dead on."Starting with the puzzle as pictured above, for the first four moves can be (1) the left center pushed out to the left, (2) the top center pushed up, (3) the right center pushed in to go out the back, and (4) the front top left corner of the puzzle pulled out, and then three more moves as shown below leave the puzzle apart (for a total of 8 moves after lifting the final piece off):




Designed by Alfons Eyckmans, made by Eric Fuller 2016.
(5 pieces, Wenge & Zebrawood, 2+5/8" x 2+5/8" x 1.75" inches)
Three standard burr shaped pieces fit into a box formed by the two Wenge (dark) pieces. Here is what the puzzle maker said:"La Taupe is a fairly simple puzzle with a level 9 solution but I found the shape and concept so interesting that I had to try making it. I'm glad I did, the solution is fun and more confusing than you might imagine with a mere five pieces. The contrast between the Wenge and Zebrawood is beautiful. This guy is a little gem! Construction of this puzzle is outstanding, with shouldered board construction and solid milled burr pieces. Fit is excellent."

Designed byStewart Coffin, purchased from Cubic Dissection circa 2006.
(five wood pieces, 3.5 inches)
The 5 pieces give the appearence of four sets of two. The solution is not unique.


Old design, level 1, no holes, notchable.
(six wood pieces, 3 inches)
The basic idea of level 1 with a key piece is described on pages 106 and 139-140 of the 1983 Hoffmann book. This one is even simpler. Pieces 1, 2, and 3 are identical, pieces 4 and 5 are identical, and piece 6 is a simple solid "key" piece that comes out first.
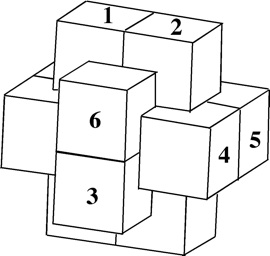
1. 2. 3. 4. 5. 6.
Assembly:1. Place pieces 1 and 2 together to form an empty rectangle shape.
2. Lay piece 3 in the bottom of the empty rectangle.
3. Place pieces 4 and 5 on either side.
4. Slide in piece 6.

Made in Indonesia 2004.
(wood, 3 inches)
Made in Indonesia 2004.
(wood, 3.2 inches)
Purchased in the 1970's.
(plastic, 2.5 inches)


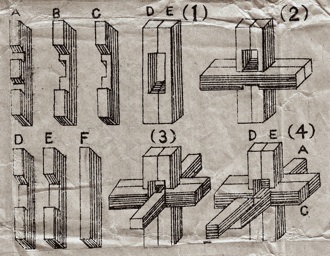
a.k.a. Double Cross
Made in Japan, circa 1930?, level 1, no holes.
(six wood pieces, each 5/16 inches square by 2.4 inches long)
Another example of a Simple 6-piece Burr. Also in the theme of pages 106 and 139-140 of the 1983 Hoffmann book, but also simpler. Two identical pieces form an empty rectangle, a double notched piece goes in the bottom, two identical pieces go on each side, and the key piece slides in:







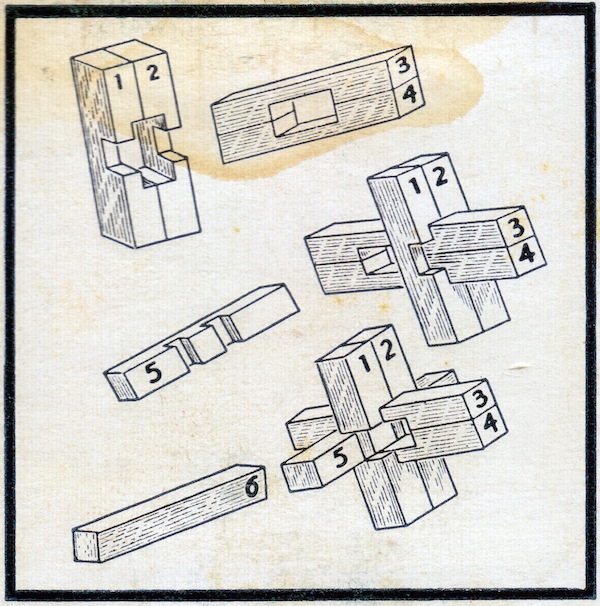



Old design, level 1, no holes, notchable., circa 1960s-1980s??
(six aluminum pieces in a cardboard box, 2+3/8" x 2+3/8" x 1/2";
directions on the back of the box are shown above)


"Made by U.N. Co. N. Y.", circa 1920?, level 1, no holes, notchable, 2x2x8 pieces.
(cardboard box, 3.2 by 2.2 by 5/8 inches, and six 1/2" x 1/2" x 2" wood pieces)
Along wth the Yamato Block Puzzle, this puzzle is discussed on page 262 of the Puzzlers' Tribute Book in a chapter by Jerry Slocum and Rik van Grol on antique Japanese export puzzles. They show a picture from the 1915 C. J. Felsman Catalog of a Mikado puzzle saying "A problem of problems ...", and note that the sililar language here, "The puzzle of puzzles ...", is further evidence that although it says NY, it may in fact be a Japanese import. Here is what is on the cover and the inside of the cover:



"Made by U.N. Co. N. Y.", circa 1920?, level 1, no holes, notchable, 2x2x8 pieces.
(cardboard box, 3.2 by 2.2 by 5/8 inches, and six 1/2" x 1/2" x 2" wood pieces)
Along wth the Mikado Block Puzzle, this puzzle is discussed on page 262 of the Puzzlers' Tribute Book in a chapter by Jerry Slocum and Rik van Grol on antique Japanese export puzzles. Here is the solution sheet that came with it and a photo of another one of these puzzles where someone has labeled the pieces:



Made in Germany, level 1, circa 1940's?
(six wood rods, 3/8" square by 2+3/8" long, with solution sheet, in cardboard box)

"Pheno-Caffein Co.,Worchester, MA, circa 1910.
(wood, 2.1 inches)
The Pheno-Caffein Co. also made the Sectional Checkerboard Puzzle, and like that puzzle, one could obtain a solution:


Designed by Stewart Coffin level 3, 3 holes.
(six wood pieces, 3.5 inches)
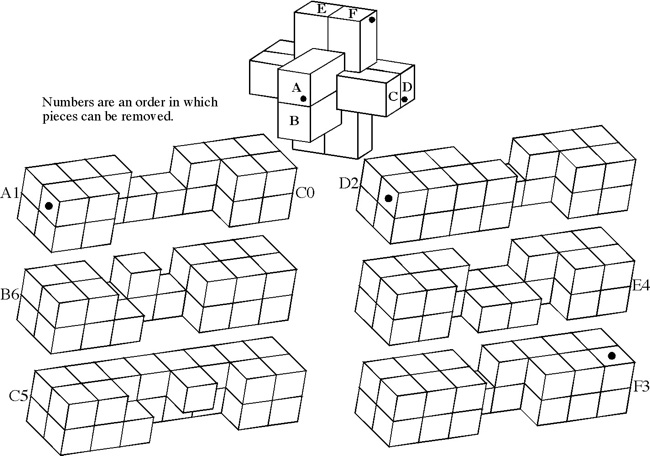

Designed and made by Bill Cutler 1984, unique level 5, 7 holes.
(Red Oak, 3 inches; 24 assemblies with a unique solution)

Discovered (by computer) and made by B. Cutler 1987, unique level 5, 7 holes.
(Mahogany, 3 inches)

Discovered (by computer) and made by B. Cutler 1988, unique level 7, 3 holes.
(Cherry, 3 inches)

Discovered (by computer) and made by B. Cutler 1988, unique level 8, 4 holes.
(Maple, 3 inches)
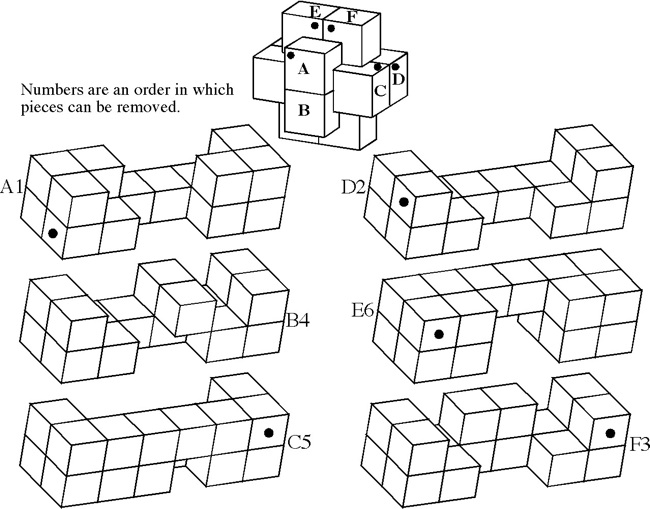

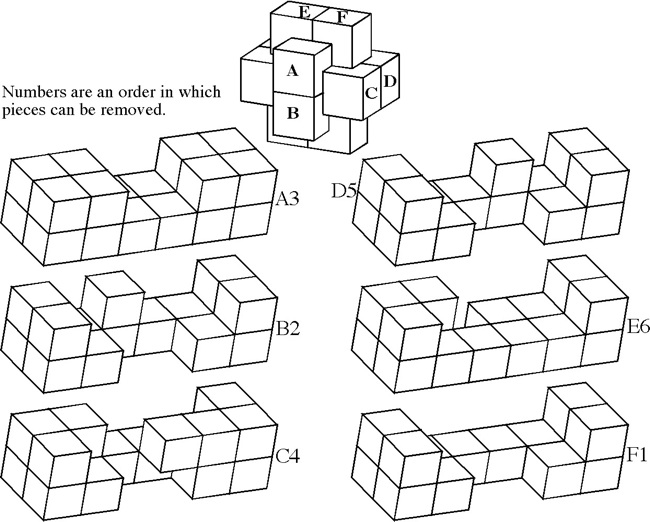
Designed by B. Cutler, made J. McFarland 2009, unique level 8, 7 holes.
(Maple / Walnut / Cherry, 2.8 inches)
Here are the first six steps:






Now the leftmost piece can be lifted up and out:


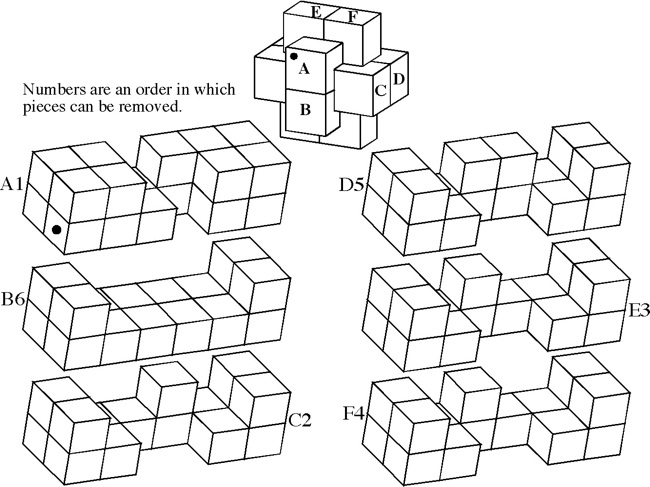
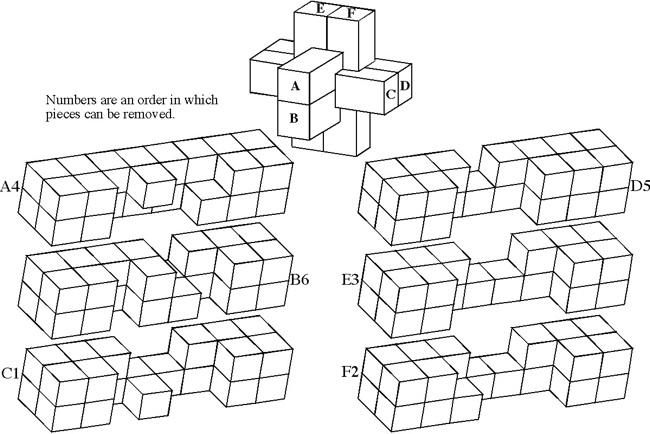
Discovered (by computer) and made by B. Cutler 1988, unique level 9, 5 holes.
(Walnut, 3.5 inches)
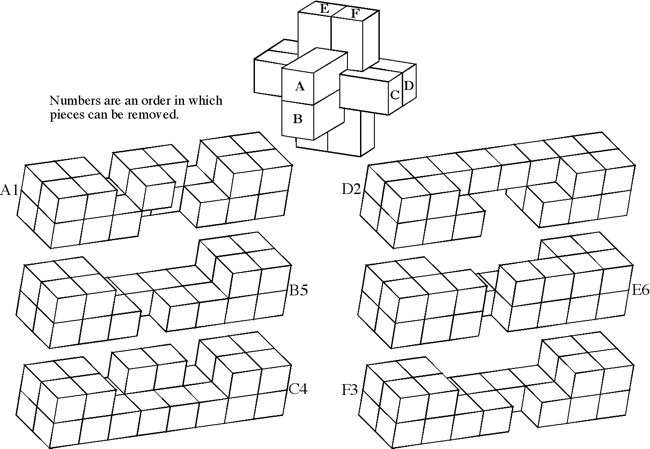

Designed by P. Marineau, made by J. McFarland 1986, unique level 9, 7 holes.
(Walnut, 3 inches)
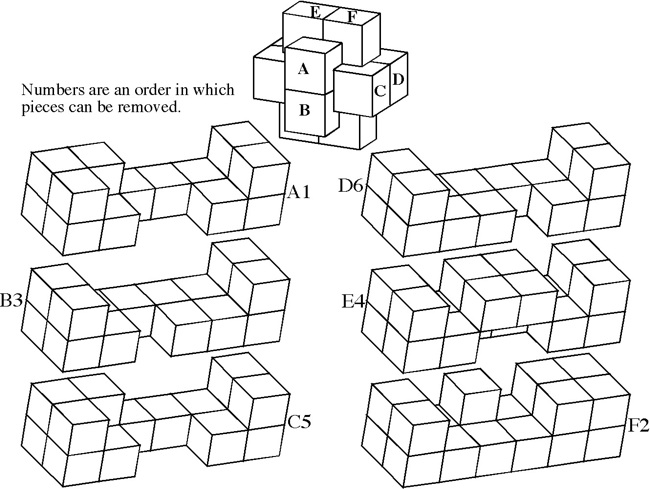

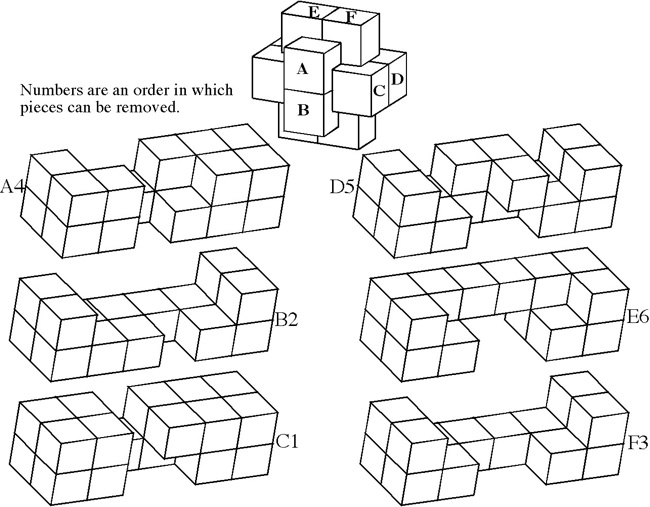
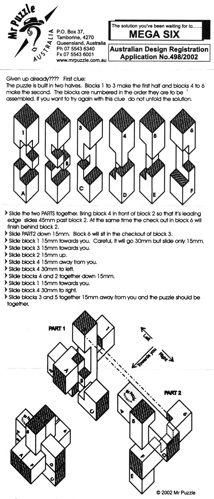
Designed by Bill Cutler 1990, unique level 10, 7 holes.
(Mahogany, 3.5 inches)
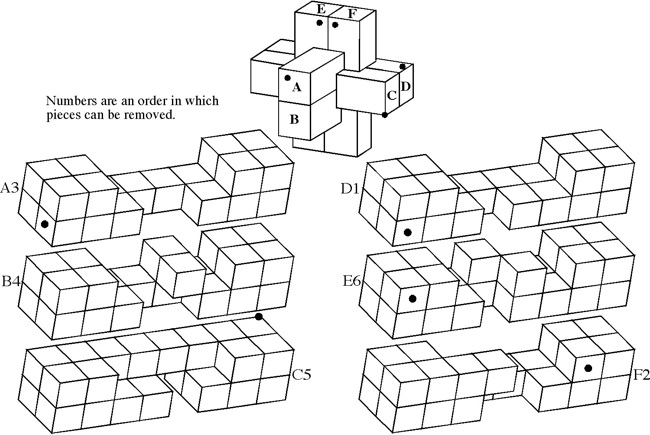
One of 18 similar unique level 10 burrs discovered by Bill Cutler with a computer program. It can be disassembled by moving (1) C /E forward 1 unit, (2) F up 2 units, (3) A back one unit, (4) D /F right 1 unit, (5) F down 2 units, (6) F forward 1 init, (7) D left 1 unit, (8) A/E back one unit, (9) B/C/F right one unit, (10) B down one unit. Note that some would consider this 11 moves since for "move" 8, both A and E can move back without dragging the other. To assemble, rather than inserting B into the pieces appropriately oriented, it may be easier to orientate things with CD facing up, and hold A/D/E (appropriately positioned) in your left hand and B/C/F (appropriately positioned) in your right hand to perform steps 10 and 9.

Discovered (by computer) and made by B. Cutler 1987, level 10, 9 holes, notchable.
(Maple, 3.6 inches)
Non-unique with solutions below level 10, but made to be unique level 10 by drawing diagonal lines on the pieces that must form a loop around the puzzle when solved.

Designed by Brian Young, made by Mr. Puzzle Australia, level 10, 8 holes.
(4.7 inches)
Unique Level 10 solution. One more hole than Computer's Choice Unique-10, with 20 assemblies instead of 7. Here is the solution that was sold with it:


Designed by Bruce Love 1987, made by Bill Cutler, level 12, 9 holes.
(Maple, 3 inches)
According to Bruno Curfs' page, Love's dozen has 89 solutions ranging from Level 3 to one of the solutions being level 12; this puzzle made by Bill Cutler has a big D drawn on a pair of the ends that forces the level 12 solution.
Further Reading
Curfs' Page, from: http://home.tiscali.nl/~bcurfs/homepage/burrs/burrs-e.htm

Designed and made by Bill Cutler; can't be disassembled.
(Red Oak, 4.5 inches)
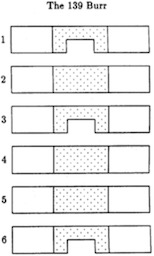
From his computer analysis, Cutler determined that 139 was the largest number of states that a standard 6 piece burr could have without having a solution, and then he chose the simplist of these for this puzzle. So this burr is made to the dimensions of a normal 6-piece burr, has lots of movement, but can't be disassembled (it was made by gluing two portions of a piece together during assembly). Here is his diagram of the pieces:

Purchased from Mr. Puzzle Australia 2006, level 1, no holes.
(six wood pieces, 3.5 inches)
Mr. Puzzle Australia credits this puzzle as being sold as early as 1875, and as having been sold under a number of names, including the Cluster, the Gem Cut Puzzle, the Chestnut Burr, and the Snowflake. When assembled it looks like a standard version of the Simple Six Piece Burr (where pieces have a diamond cross section). However, it actually is composed of six identical pieces where two assemblies of three slide together.


Made in Japan circa 1930?, level 1.
(cardboard box and 6 wood pieces, 3.75 inches;
box cover similar to other vintage Japanese exports like the Yamato Puzzle)

Made in Japan circa 1930?, level 1.
(cardboard box and 6 wood pieces, 3 inches;
box cover similar to other vintage Japanese exports like the Yamato Puzzle)
Here is the solution sheet that came with it:

Designed by Bill Cutler 1965, purchased circa 2000, level 1.
(six wood pieces, 3.5 inches)
Six identical pieces with some angled internal cuts that slide apart simultaneously.

Discovered (with a computer) and made by Bill Cutler 1989, level 5, 7 holes.
(Maple, 3.5 inches)
A programmer's nightmare because disassembly requires a twist. Move F up 1/2 unit, rotate A 90 degrees, move A up (pulling F with it by 1/2 unit), move D up, slide D out. Note that although the 1/2 move is needed theoretically, there is enough play in the puzzle that F can initially be moved up a full unit (this does not change the level since A has to be moved up in any case). This puzzle is hard for a person too, because according to Cutler's computer analysis, there are 102 assemblies (ways these pieces can exist in space in the solved shape) with only this one solution (the only way that is achievable starting with the pieces apart).

Designed and Made by Bill Cutler 1994, level 7, 4 holes, notchable.
(Cherry, 2.25 inches)
Bill Cutler credits Stewart Coffin with the idea of making burrs with slanted pieces in a way that restricts the number of possible assemblies. Cutler then found a non-unique level 7 burr from his computer analysis which became unique when made with slanted pieces. Slide F forward, slide E left (pulling D with it), slide E forward, push D right, slide F back, slide F right, remove A:


Designed by Gregory Benedetti, made by Eric Fuller 2017.
(6 pieces, Ambrosia Maple, 3 inches square)
Many angled cuts for an unusual assembly. Here is what the puzzle maker said:"With the invention of the NOS (New Old School) puzzle series, Gregory took the six piece burr format and turned it on its head. The only thing more noteworthy than the uniqueness of the series was how difficult they are to make. When he originally send me the plans, I turned him down because it just looked like a nightmare to manufacture. I changed my mind after handling a couple 3d printed prototypes. These look like traditional six piece burrs but are nothing like them. The angled internal geometry allows for some outrageous movements. They are very confusing and wonderfully different. This is the final three designs to complete the set. Construction was very challenging, requiring the creation of several new jigs and techniques. "Seizaine" is the seventh and final of the NOS designs and has the highest level. A full sixteen moves; Greg says he used "Love's Dozen" as the base but all I see is crazy angles and some woodworking challenges that were VERY difficult. Fit is very good, a little loose to account for dry conditions during the period in which it was made. This puzzle is delivered assembled."

Designed by Bill Cutler.
(Walnut, 3 inches)
Slide F back and then remove the three pieces A, C , E simultaneously by expanding them out to the upper left:

Designed by Bill Cutler1986, spin + level 3.
(Red Oak with two steel ball bearings, 3.5 inches)
Spin the puzzle in the orientation shown (around the axis defined by E and F) to position the balls, and then the two halves A,C,F and B,D,E can slide apart with three moves:


Designed by Gregory Benedetti, made by Maurice Vicourouz 2012.
(Purple Heart, 3.25 inches)
Pieces are a small cube trapped in the center, three identical "simple pieces", and three identical "complex" pieces. Assembly is relatively easy, where the three complex pieces and the cube are put compactly together as shown on the left in the figure below (rubber bands keep them together for the photo) and then the three simple pieces slide simultaneously over the exposed corner:

Disassembly requires simultaneous motion to move the three complex pieces together into the "key position" shown on the left below. One first has to identify which three are the complex pieces and then carefully jiggle and push to get all three to push in flush. In the middle is this position lit up from the back (where the serial number of the lower in-out piece can be seen), and on the right is shown the top three pieces coming apart simultaneously. The puzzle's name comes from the fact that when you don't know what is inside this puzzle, disassembly may be achieved by accident when randomly shaking and pulling on the puzzle.




Designed by Matti Linola, made by Eric Fuller 2010.
(Yellowheart and Wenge, 3 inches)
Once one sees how to solve the three piece burr formed by the light colored pieces, the dark pieces don't change the puzzle very much, but the construction and fit is terrific.
To solve:Here are photos of the assembly progressing:
- Take out the dark pieces, to first solve the 3-piece burr.
- Start with the simple U shaped piece and see that because each piece has to slide over one of the other two, there is only one way the other two can go, and then assemble the three pieces.
- Now look down each end, and it can be seen that there is only one way the dark pieces could possibly fit.
- Then take apart the three light pieces, insert the dark pieces, and push everything back together, moving the dark pieces in and out as needed.








Designed by Steve Nicholls and Ali Morris, purchases 2019.
(7 brass cylinders, where two go together to make a total of 6 cylinders, each 2.75" long)
A combination of a trick take-apart puzzle and a 6-piece burr. Looks like a 6-piece burr when assembled, but it is actually 7 pieces where half of the key piece unscrews (not a burr move). The other half of the key piece is held in by a pin so it does not fall out and is not the first piece to be removed (not a standard burr feature). Here are photos of the puzzle being assembled:








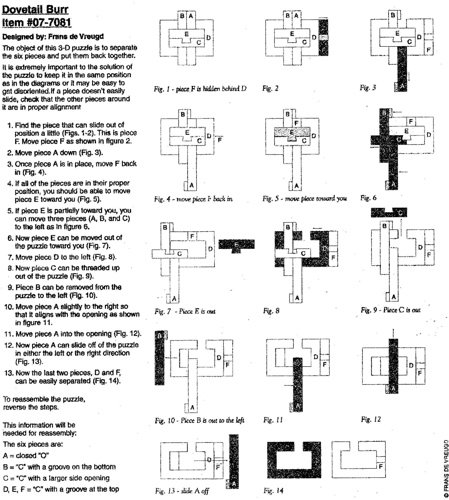
Designed by Frans de Vreugd 2005, purchased from Mr. Puzzle Australia.
level 5, 3 hole, notchable, six 2x2x6 pieces with end caps.
(Queensland Silver Ash with Queensland Blackbean ends, 3.125")
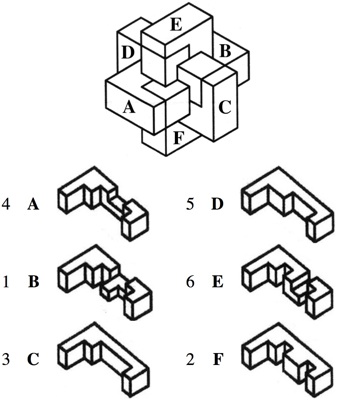
A variation of the standard 6 piece burr where end caps have been added to the pieces; highest level for this type of burr with notchable pieces. Here is a diagram of the puzzle and the pieces (numbers are the order they can be removed):



Designed by Stewart Coffin (puzzle no. 9), made and sold by Interlocking Puzzles 2000.
(wood, 6 identical pieces and 6 corresponding identical pieces, 2.6 inches)
A variation of the 1890 Altekruse burr with pins and holes for some of the notches; shown on page 79 of the Coffin Book. Below are photos of one way for inserting pieces 3 through 11; piece 12 is then added to complete the two halves as shown above, which then slide together.











Designed by Frans de Vreugd, purchased from Bits and Pieces 2007, level 6.
(wood, 3.75 inches)


Designed by Stewart Coffin (design number 105)
Sold in 2006 by Cubic Dissection (www.cubicdissection.com)
(left Bocote / right Cocobola, both 3.25 inches)
Can be solved in two ways using the same pieces; the left above is solved using coordinate motion (all pieces moving together at the same time), and the right above is solved by halving two halves that slide together. The hardest part is trying to visualize what it should look like together once it is apart. Here is what the two solutions look like when starting to come apart:



a.k.a. Triple Play
Purchased from Bits and Pieces 2007.
(wood, 3 inches)
Looks like three pieces but is actually a level 1 non-standard 6 piece burr (six pieces (three light wood and three dark wood pieces). Here is the solution that came with the puzzle:


Designed by F. Potts, made by E. Fuller 2008, purchased from Cubic Dissection.
(Walnut and Maple, 3 inches)
Six pieces with magnetic tips assemble to look like a three piece burr (e.g., Just The Three). The pieces are all identical; here are photos of different views of them:

Here are photos of pulling apart the whole assembly and an assembly of four:


The solution is almost as much of a dexterity puzzle as a logic puzzle, where there is only one way to put two together that will lead to a solution, then it is easy to spread them apart and put in the next two, then harder to spread apart the four to get in the fifth, and then after pushing everything back together, a bit tricky with only two hands to get in the sixth piece. Here is a photo of the assembly of four with the two remaining pieces still to be put in:


Designed by Gregory Benedetti, made by Eric Fuller 2011.
(Acrylic, Yellowheart, 2.25 inches)
Here is what the puzzle maker said about this puzzle in the sale listing:"Reminiscent of Padaung Rings, this nifty little pocket puzzle is a lot of fun to solve. With a level 14.4.2 it's tricky but not impossible ... once you get the correct alignment and piece selection, it flows fairly quickly."


Copyright ThinkFun 2010.
(plastic, 2.75 inches square)
Comes with a solution booklet that has 37 steps to disassemble reading forward and 37 steps to assemble by flipping over the booklet and reading in the other direction.
Further Reading
Booklet pages.


Designed by Adin Townsend, made by Eric Fuller, 2017.
(Wenge, Canarywood, Granadillo, Maple, 4" x 4" x 2")
Here is what the puzzle maker said:"Amulet is a tricky and interesting variation on the standard six piece burr. To quote Allard's blog post about it: "He’s fiddled around with a standard six-piece burr and added a few constraining voxels around the middle and shorted one of the axes… adding those voxels makes all the difference it turns out – without them there’d be 144 solutions, with them the solution is unique… and quite tricky!" Construction of this puzzle is excellent, with a nice fit that will tolerate a fair amount of movement."



Designed by Noah Prettyman, made by Eric Fuller, 2018.
(6 pieces, Ash and Wenge, 2.24 inches square)
Two standard looking 6-piece burr pieces, two plate burr pieces, and two irregular pieces, one of which is the first to come out, as shown on the upper right above. Here is what the puzzle maker said:"Combined Burr is just a crazy puzzle that I had to make. Six pieces come together to form the familiar burr shape. Two standard stick pieces, two board pieces and two very unusual "I'm not sure what's going on here" pieces. With a whopping level 4.18 solution, this one will keep you guessing during assembly and disassembly. Crafted with Wenge and Ash, this burr is precise and well made. Shoulder joints along the length of the board burr pieces allow for the color contrast necessary without compromising strength."


Designed by Noah Prettyman, made by Eric Fuller 2017.
(6 pieces, Black Limba, 3 inches square)
Six irregular pieces form a shape like a plate burr. Here is what the puzzle maker said: Here is what the puzzle maker said:Noah Prettyman designed this wonderful new burr puzzle with the intention to recreate the standard six piece burr shape using puzzle cube type pieces. A very unique idea, and a successful one given the unique level 6.3 solution. Knotted burr is a lot of fun to solve and is quite difficult despite its reasonable seeming number of moves. I'm looking forward to whatever he comes up with next!



Designed by Chi-Ren Chen, made by Eric Fuller 2012, unique level 2.
(Walnut, Ash, American Mahogany, 3")

Designed (with a computer) by Bill Cutler and Frans de Vreugd 2001, level 13
(Hard Maple and Jatoba, 2.25 inches)
Two 1x4x6 pieces in each dimension. Making top dark wood and the bottom light wood makes the level 13 solution unique. The number of "holes" (internal voids) is 13 because the volume of assembled shape if it was solid is 104, and adding up the volume of the six pieces gives 91. Here are sheets that came with the puzzle (copyright by and courtesy of Bill Cutler).


Purchased from ThinkFun 2006.
(plastic, 6 pieces, 2.75 inches)
Made by D. Alsmeyer 2007, Sabriday Puzzles.
(6 different woods, 3.5 inches)
The booklet that comes with the retail plastic puzzle shows 65 steps to completely take the puzzle apart. McFarren's Page shows a solution that removes the first piece in 28 steps, and completely takes the puzzle apart in 35 steps.
Further reading:
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/gordian.htm
Sabriday's wood description (Mahogany, Maple, Cherry, Purpleheart, Walnut, Paduk).


Designed and made by Franz de Vreud 2003, unique level 16.
(Maple and Granadillo, 2.9 inches assembled)






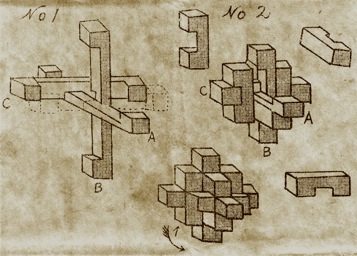
These were made in Japan and owned by J. A. Storer in the 1960's. The Cleverwood Page credits these simple types of burrs to Tsunetaro Yamanaka (born 1874) and his descendants; here is a diagram of a cube from the 1942 Filipiak book, and an inexpensive circa 2000 plastic ball:

Further Reading
Cleverwood Page, from: http://www.cleverwood.com/kumiki.htm


Wm. F. Drueke & Sons, Grand Rapids, MI, circa 1940's?
(wood pieces in cardboard box, 2+5/8" x 2+5/8" x 2+5/16" high)
Examples of some classic relatively simple burrs that have been made by many over the years (e.g., see the Japanese Shape Burrs). Historical acounts indicate that Bill and Marian were Drueke family names.
Further Reading
Drueke Family History, from: www.peterspioneers.com/WRSD.htm
Drueke Directory, from: www.peterspioneers.com/WRSDdir.htm
C. Bloom Grand Rapids Press Article, from: www.peterspioneers.com/WFD.htm
Cribbage Board Article, from: http://www.cribbageboardsonline.com/article2005b.pdf

Designed by Stewart Coffin, Made by Eric Fuller 2012.
(7 pieces, Canarywood, a 13/16" cube and 6 pieces 3" long by 13/16" square)
Six burr pieces assemble with coordinated motion into a standard 6-piece burr shape with the cube trapped in the middle. t is a non-standard 6-piece burr design with the 7th cube piece added by the puzzle maker to stabilize the puzzle. I found the maniputlation of these pieces not as pleasant as I expected and gave up (for now). Here is the description quoted from the puzzle maker's page:"This puzzle was Jarry Slocum's exchange puzzle at IPP18. I was recently visiting a puzzle friend and saw it on the shelves. Spent some time working with it and finally solved it... HAD to make it. Since John Rausch did such a nice job writing up a description on his site, I think I'll plagarize from it directly:"Four of the six pieces have diagonal notches on both sides of the large, simple notch. Two pieces have them on only one side. Normally, a six-piece burr consisting only of pieces with a single, large, simple notch could not be assembled. With the diagonal notches described, it becomes a coordinate motion puzzle - a difficult one! Number 129a in Stewart's numbering system. He made 100 in 1998."I have modified the design a little bit based on Nick Baxters advice - instead of two pieces having only one notch, one piece does (leaving the other five with double notches). After some experimentation I felt that this configuration was the trickiest, and really made the solver grasp the concept behind the puzzle. Finaly, this puzzle is by nature very loose when solved. It's just a function of the notch location. I hate loose puzzles, so I included a 7th piece, which is an internal cube with magnets. This doesn't really add to the assembly, but it keeps the puzzle nicely together once solved. Happily it also makes the puzzle much more difficult to disassemble!"

Designed by Junichi Yananose, made by Eric Fuller.
(7 wood pieces, 3 inches)
Looks at first like a standard 6-piece burr. However, one of the apparent pieces is really two pieces (the one marked with a red dot in the above photo). Here is what the puzzle maker said:"At first glimpse this puzzle looks like another 6 piece burr iteration. However, disassembly will show that it holds a surprise! One of the pieces has been split, creating a very unique 7 piece burr with quite a tricky solution. Internal voids make this a level 6 burr and also create many unassemblable solutions that will frustrate the solver. This is a difficult puzzle to solve."



Designed by Yavuz Demirhan, made by Eric Fuller 2018.
(Paduak frame, 2 Wenge pieces, 2 Holly pieces, and two Acrylic pieces,
7 pieces total, 1+3/8" x 1+3/8" x 1+1/8" inches)
A tiny puzzle that came in a little pink bag. Here is what the puzzle maker said:"As soon as I saw the Gaia design I knew I wanted to make it. The structure is very unique, incorporating stick pieces and board pieces with a constraining cage. The unique level 11.2 solution is not as difficult as you would think, making this a fairly approachable puzzle. When solved the acrylic nicely sets off the three wood combination. Fit is very precise, and the cage features rabbited joinery for strength. Stick pieces are milled from solid wood."


Designed by Aleksandr Leontev, made by Eric Fuller 2016.
(8 pieces, Wenge, Zebra, Quartersawn White Oak, 2+9/16 inches square)
Looks like 12 pieces with four in each direction, but actually there are four standard burr shape pieces and four T-shaped pieces that join two rods together. Here is what the puzzle maker said:"Elena's burr is an interesting variation with a lot of tricky movement. The level 13.7 solution will keep you very very busy. Disassembly alone is a feat, with lots of dead ends. Reassembly without directions is extremely difficult. Elena's burr is an elegant design, and the ability to come up with a unique solution at such high levels with such simple pieces is an achievement. I really enjoyed making and playing with this one! Construction of this puzzle is superlative. Fit is dead-on and the pieces slide with the perfect amount of friction. I really like how this one turned out....it's possibly the best of the update."

Made in Japan, circa 1930?, level 1, no holes.
(cardboard box, 2.6" x 2.1" x 7/16", 9 wood pieces, and solution sheet;
box cover similar to other vintage Japanese exports like the Yamato Puzzle;
this puzzle was also made in a 22-piece version)
Here are photos of basic solution steps:









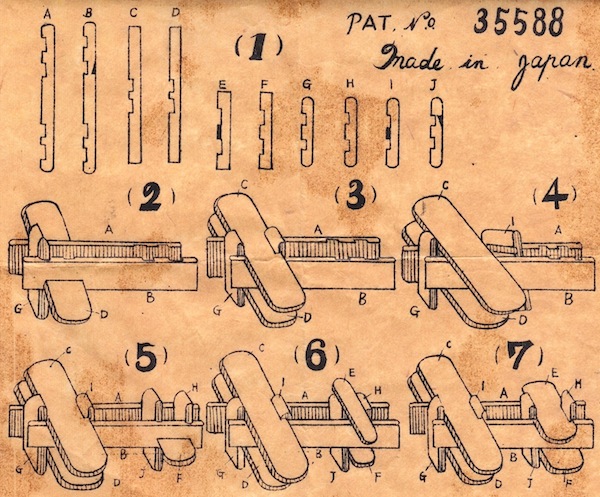
"Patent number 35588, Made In Japan", circa 1920's?
(10 wood pieces in a 3.75" x 2.4" x 1/2" cardboard box)
Easy to see how it goes together, but a bit of a dexerity puzzle to put the final piece in; two of the rectangle pieces have bevels to make that work (on on the inside middle and one on both edges).

Designed by P. McDermott, made by B. Young and P. McDermott,
purchased from Mr. Puzzle Australia in 2007, level 6.
(wood, 10 pieces, 3.25 by 6.25 by 2.5 inches)
Here are the directions and solution that were sold wih the puzzle:




Designed by Bill Cutler.
(wood, 3.5 inches, 11 pieces and 5 ball bearings)
Eleven pieces in a 2-4-5 configuration. Takes 5 balls (it came with 4 inside and you are asked to put the 5th in). Two are in a notch near the top of 11. The other three can be in a portion of the bottom part of piece 11 when it is pushed up, but in order to get 11 in place, they must be shaken out into other places that lock up the other pieces. Number the ends as follows:
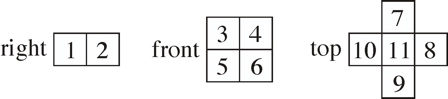
Disassembly:1. Jiggle the balls if necessary and move 11 up. 2. Two balls are always in a notch near the top of 11; jiggle the other three so that they are in a cavity at the bottom of 11. 3. Slide 8 up (1 and 2 get dragged with it). 4. The balls will now all fall out. 5. Slide 5 out. 6. Slide 11 out. 7. Slide 3 and 10 out. 8. Remove 7 and 9. 9. Remove 4. 10. Remove 6. 11. 1, 2, and 8 now come apart.Assembly:1. Assemble the puzzle without the balls by reversing the disassembly. 2. Slide 11 and 8 up (8 gets 1 and 2 dragged with it). 3. Put the two balls in the top and then slide a pencil through the puzzle to keep them from coming out. Then turn the puzzle over and put the other three balls in. 4. Slide 8 down (dragging 1 and 2 with it) as you carefully remove your pencil. 5. Shake the three balls so they leave the bottom of 11; then slide 11 down.



a.k.a. Hexsticks, Notched Hexagonal Sticks
Patented by S. Coffin 1973, made by 3M 1970,
also discovered independently by B. Cutler.
(12 plastic pieces, 3.5 inches)
Three solutions for assembling the twelve notched sticks are described on pages 116-118 of Coffin's book. The package is shown above; it has the directions on the bottom (also shown above) and inside is a hexagonal shaped solution booklet. Below are two panels from each side (other three are shown on the next page):


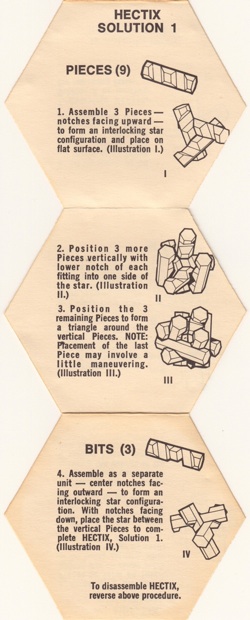
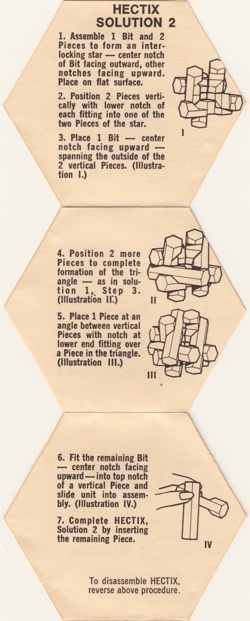
Further Reading
Coffin Patent, from: www.uspto.gov - patent no. 3,721,448
Cutler's Hectix Page, from: http://home.comcast.net/~billcutler/stock/hectix.html
Cutler's Hectix Revisited Page, from: http://home.comcast.net/~billcutler/stock/revisited.html

S.S. Adams Co., 1961.
(12 plastic pieces, each 1.5 by 3/8 by 3/8 inches)



S.S. Adams Co., 1961.
(12 plastic pieces, each 1.5 by 3/8 by 3/8 inches)


Purchased from Bits and Pieces 2007.
(10 wood pieces with solution sheet, 4.5 inches;
shown as "The Mystery" on pages 107-108, 141-142 of the 1893 Hoffmann book)

Copyright 1991-2007 Junichi Yananose, purchased in Japan 2010.
(aluminum, 12 pieces, 3.5 inches square)
Here is the box and the text on the front and back:



The puzzle slides apart in two halves and a free piece:


Designed by Bill Cutler and made by Jerry McFarland 2003.
(Walnut, 12 pieces, 2 by 2 by 8 inches)
Here is the sheet that came with the puzzle (copyright by and courtesy of Bill Cutler):

Designed by Bill Cutler 1981.
(Maple / Walnut / Cherry, 3.7 inches, 12 pieces)

Designed by Bill Cutler 1982.
(Maple / Walnut / Cherry, 4 inches, 13 pieces)


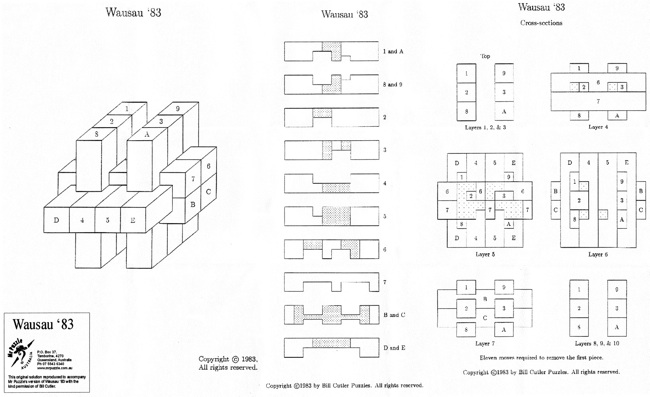
Designed by B. Cutler in 1983, made by Mr. Puzzle Australia 2008, level 11.
(Queensland Silver Ash / Queensland Blackbean / Mackay Cedar, 14 pieces, 4";
sold with directions and solution shown above)

Designed by B. Cutler 1984, made by E. Fuller 2008.
(Maple / Walnut / Mahogany, 15 pieces, 4 inches)

Designed by Bill Cutler and made by Jerry McFarland 2000.
(wood, 3 inches, 13 pieces + 2 pins)
Looks like the Wausau '82 puzzle, but different inside; here are excerpts from the puzzle sheet (copyright by and courtesy of Bill Cutler):
- Position the puzzle on a table so the group of three are vertical and the group of six with the dot is facing you, with the dot on the right (upsidedown from the figure).
- Give the puzzle a hard spin clockwise to move the pins into their holes.
- Simultaneously, the center rod of the three goes up, the rod with the dot comes out toward you, and the rod to its left goes back away from you. You will see the pins in the ends of the rod with the dot and the one next to it (take them out so you don't lose them).
- Now the puzzle comes apart.
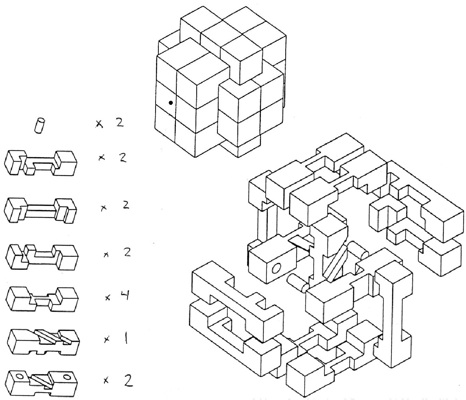

Designer unknown, made by Eric Fuller.
(Purpleheart / Maple / Lacewood, 13 pieces, 2.25 by 3 by 3.75 inches)
Here is what Eric Fuller says:"This 13 piece interlocking burr puzzle was published in the magazine Soumen Kuvalehti number 11 in 1926. There are 2 possible solutions, both very similar. Despite its not being a high level puzzle, the solution is surprisingly tricky, probably because of its unusual shape. Ishino Keiichiro posted it on his site and Matti Linkola discovered the magazine."


Level 1, circa early 1900's??
(4" wood box with directions and 18 wood pieces, 3.6 inches assembled;
right vertical piece in photo above is solid key piece.)

Designed by Bill Cutler 1975.
(Maple / Walnut / Cherry, 3.6 inches, 18 pieces)

Designed 1992 and made by Jerry McFarland, purchased from cubicdissection.com 2008.
(Walnut, Mahogany, Maple, 19 pieces, 3.5" by 2.6" high, 7/8 inch square sticks)
Disassembly involves manipulating the central 4 pieces like opening a lock.
Here is the diagram of the pieces from the solution sold with the puzzle and photos of removing three pieces:


Further Reading
Solution that was sold with the puzzle.

"Made in Japan K.K.", circa 1920's?
(20 wood pieces, 4 inches;
box cover similar to other vintage Japanese exports like the Yamato Puzzle)
Two pairs of identical 4" pieces, four identical 2.5" pieces, eight identical 1.3" pieces, and four identical 1.3 inch solid pieces assemble to a somewhat two-dimensional snowfake arrangement; here is a photo of the box and the solution sheet:



Purchased from Pentangle Puzzles 2007.
(wood, 7.5 inches, 20 pieces)
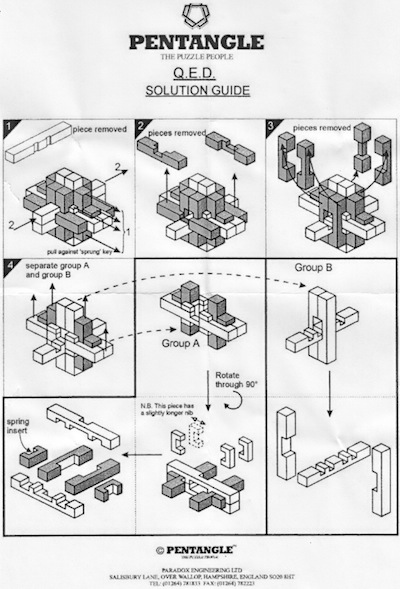

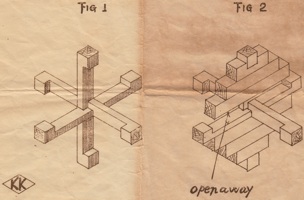
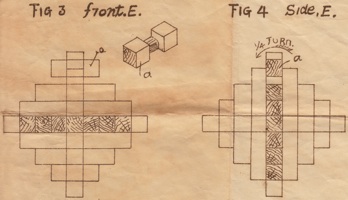
Made in Japan, circa 1930?, level 1, no holes.
(cardboard box, 4.1" x 3.4" x 1/2", 21 wood pieces, and solution sheet;
this puzzle was also made in a 9-Piece Version)

Designed by Bill Cutler and made by Jerry McFarland 2003, level 85.
(Cherry / Walnut, 21 Pieces, 3 by 3 by 3.6 inches)
The Binary Burr functions like the Chinese Rings puzzle:

There are six "ring" pieces that must be manipulated in order to remove the "bar" piece; the remaining 14 pieces don't move and form the "cage' that constrains the movements. It basically takes two moves for each move of the corresponding Chinese Rings puzzle.

Designed by Bill Cutler 1978, made by J. McFarland 2012.
(24 Maple, Walnut, and Cherry 3/4" rods, 5.25" square assembled)

Designed by Bill Cutler 1978, made by J. McFarland 2012.
(24 Maple, Walnut, and Cherry3/4" rods, 4+3/8" square assembled)

PDesigned by L. Kleinwaks, made by Eric Fuller 2013.
(Walnut, Cherry, Maple, 2.25" x 2.25" x 4")

Purchased from Interlocking Puzzles 2000.
(wood, 2.5 by 2.5 by 9.8 inches)
Four standard 6-piece burrs that share one dimension. Pieces 4, 8, and 10 are identical, pieces 1, 5, and 15 are identical, pieces 12 and 16 are identical, pieces 11 and 14 are identical, and pieces 9 and 13 are identical:
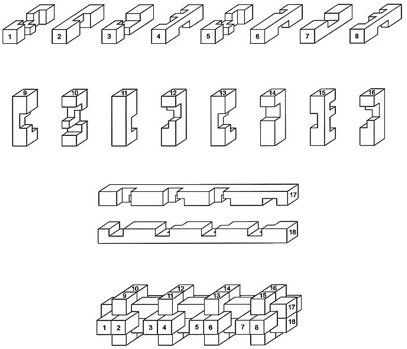

Designed by Wayne Daniel 1982, made by Interlocking Puzzles.
(wood, 4.8 inches)
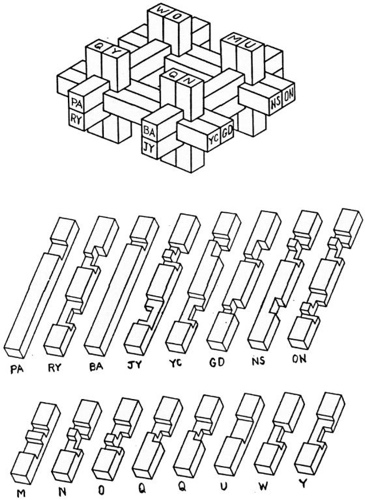

a.k.a. Eight Burrs
Designed by David Bruce, made by Interlocking Puzzles 2000.
(wood, 24 pieces, 4.8 inches)
The basic idea is to combine two eight piece assemblies and then add eight "outer" pieces. Here are diagrams of the pieces from the solution that came with the puzzle:
Assembly A pieces:
Assembly B pieces:
Outer pieces pieces:

Further Reading
Lost Day solution that was sold with the puzzle (pdf 9 pages).

Purchased from Interlocking puzzles 2002.
(13 ply Baltic Birch rings 7.2", Australian Jarrah rods 2.25", 18 pieces)
Four 6-piece burrs connected in one dimension by a pair of rings. Requires multiple counter rotations of the rings to disassemble or assemble. Interlocking Puzzles said:
"The eight radial pieces have slightly angled notches and can be sorted into four right handed and four left handed pieces. The eight axial pieces have normal notches. The four unique higher level burrs are distinctly different. The lengths of the burr rods are greater than 6 units. If these were four stand alone burrs they would require five, four, or three moves to get the first piece out. One of them would also require three moves to get the second piece out. It is a fun challenge to assemble each individual burr onto the rings and then remove it before facing the larger challenge of the whole puzzle."


Purchased circa 2000.
(plastic, 2.25 inch cube with 3D cross)
Similar idea to the Two Piece Oddity, with a frame and a 3D cross like piece that has to be removed.

Designed by Tom Jolly, made by Eric Fuller circa 2000.
(T'Zalam, 3 inches)
A frame and a 3D cross like piece that has to be removed.

Designed by Osanori Yamamoto, made by E. Fuller 2013, Level 14.
(Jatoba and Purpleheart, 2.25" x 1.5" x 1.8")
To disassemble, exchange the two trapped pieces, maneuver a bit, and then the two can be manipulated out of the cage; here are some selected positions:







Designed by Tyler Hudson; made by Eric Fuller 2023.
(Macacauba frame and two Bocote pieces, 2+5/8 inches)
Remove the pieces from the frame (and put them back). The pieces are so constrained, that just first determining how they can individually be put in guides the assembly start:









Designed by Stephane Chromine, made by Eric Fuller, 2011.
(Walnut and Yellowheart, 3" x 2.25" x 1.5")
The top two pieces are identical. Different assemblies are possible depending on how the top two pieces are rotated. In their easiest positions, the bottom piece can be removed in 8 moves. However, in one configuration, 12 moves are required to remove the bottom piece (given a reasonable way of counting rotations). Below are 9 of the positions for disassembly starting with the top piece rotated as the puzzle was shipped. Although the middle piece starts in its correct rotation for the final steps of disassembly, after pulling out and tilting down the bottom piece, the middle piece is rotated and drops down to allow the top piece to be rotated, and then the middle piece can be pushed up and rotated back so that the top two pieces are together and up to allow the bottom piece to be removed. Note that it now takes only 8 steps to put the puzzle back together by leaving the top two pieces in their existing rotations.











Designed by Ramos & Abad, made by Pelikan 2006, level 13.
(wood, 2.4 inches)



a.k.a. Internal Combustion
Designed by Tado Muroi early 1990's.
(left: "Pandora's Box", Mr. Puzzle Australia, Queensland Blackbean, 3.5x3.5x2.25";
right: "Internal Combustion", Bits and Pieces, Aluminum, 2.25" x 2.25" x 1.5";
described in Boardman's book)
Four burr pieces (two of which are identical) in a frame. Below is a 9-step assembly (6 steps to remove the first piece) based on the piece orientations shown on the right above (except in the photo above the left two have been flipped upside-down for better viewing):
1.2.
2.

4.5.
6.

7.8.
9.

A 12-step assembly where the piece labeled 3 is reversed from the 9-step assembly shown on the preceding page:

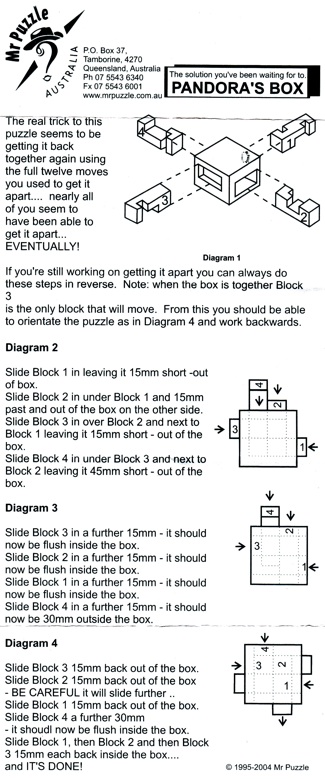
A 15-step assembly (see also the Boardman book):
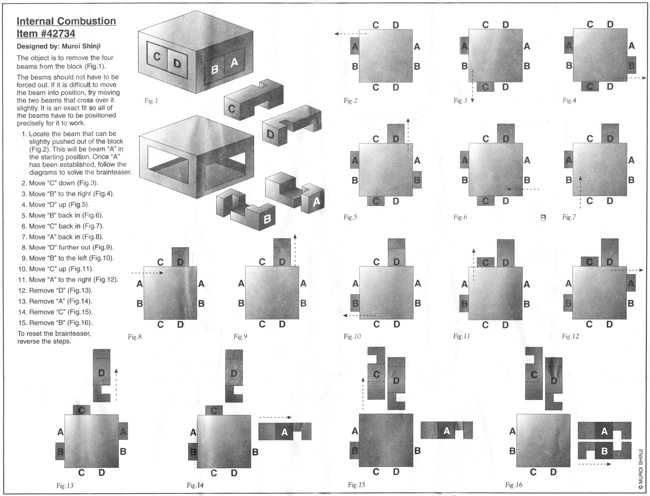










Designed by Yavuz Demirhan, made by Eric Fuller 2013.
(Sapele and Imbuya, 2.25" square, level 4)

Purchased from Bits And Pieces, 2008.
(wood, 3.4 inches square assembled by 7/8 inches thick, with solution sheet)

Designed by Gregory Benedetti, made by Eric Fuller 2012.
(Sapele and Wenge, two halves of the cage and 6 pieces, 2+5/8" square)



Designed by Logan Kleinwaks, made by Eric Fuller 2013.
(right, "Bookend Burr", Holly, Walnut, Ash, 2.5"x2.25"x2.75", level 10;
(middle, "Clamped Burr", Holly, Walnut, Ash, 2.25"x 3"x2.6", level 15;
right, "Cornered Burr", Walnut, Cherry, Ash, 2+5/8" square, level 14)
Beautifully made with high levels for rectlinear moves solutions. Shorter solutions may be possible with non-rectilear moves. For example, to remove a piece from the Cornered Burr with just three moves and some additional twisting, start by sliding the top piece to the right (if it looks like on the left below, re-orient the puzzle so it looks like the right photo below), then slide the front piece left, then up, and now, although it is easier by first sliding the bottom piece to the right, it can be twisted out without any further movement of other pieces.







Sold by Interlocking puzzles 2000.
(wood, 2.5 inches)
The only set of 6 notchable pieces that can be assembled into 6 different level 1, no-hole, standard six piece burrs. Here is the solution that was sold with the puzzle:



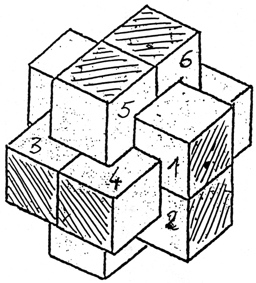
Designed and made by Jean-Claude Constantin, purchased used 2006.
(13 pieces, set is 6.25" x 3.25 x 2.5 inches, each piece is 3/4 x 3/4 x 3 inches)
A set of 13 pieces to make 40 different notchable 6 pice burrs; the same set of 6 is sometimes used for several different problems (pieces in different positions). Each piece is 2 by 2 by 8 units.
JCC's 40 Problems:
1. ADFIKL
2. ADFIKL
3. ABDKLM
4. ABDKLM
5. ABDKLM
6. ACDKLM
7. ACDKLM
8. ACDKLM09. ADGHKL
10. ADEJKL
11. AFGIKL
12. AFIJKL
13. AEGIKM
14. AFHJLM
15. ADHIKM
16. ADEFLM17. ACGKLM
18. ACGKLM
19. ACJKLM
20. ACJKLM
21. ABGKLM
22. ABGKLM
23. ABJKLM
24. ABJKLM25. ADEIKM
26. ADEIKM
27. ADFHLM
28. ADFHLM
29. AGHIKM
30. AGHIKM
31. AEFJLM
32. AEFJLM33. BCFIKL
34. BCFIKL
35. BEFHIM
36. BEFHIM
37. BEFHIM
38. BEFHIM
39. BEFHIM
40. BEFHIM
JCC's Solution Hints:
1. AK-LI-FD
2. AL-KF-DI
3. AM-IK-BD
4. AL-MK-BD
5. AK-ML-DB
6. AD-MC-KL
7. AD-KC-ML
8. AD-LC-KM09. AL-KH-GD
10. AK-LE-DJ
11. AK-GF-LI
12. AL-JI-FK
13. AK-GE-MI
14. AL-JH-FM
15. AD-IH-KM
16. AD-FE-ML17. AL-KC-GM
18. AM-KC-GL
19. AK-LC-MJ
20. AM-LC-KJ
21. AK-MG-BL
22. AK-LG-BM
23. AL-MJ-KB
24. AL-KJ-MB25. AK-ME-DI
26. AM-KE-DI
27. AL-MH-FD
28. AM-LH-FD
29. AM-IH-KG
30. AK-IH-MG
31. AM-FE-JM
32. AL-FE-JL33. BI-LC-FK
34. FB-CK-LI
35. BE-HF-MI
36. BH-EI-FM
37. FH-EM-BI
38. EI-MH-FB
39. EH-FM-BI
40. EH-MI-FB

Purchased from Creative Craft House 2007.
(wood box 3.4" x 9.25" x 4.1" with 27 wood pieces, each 3.1" long by 3/4" square)
This set has 27 2x2x6 unit standard 6-piece burr pieces numbered from 0 to 26, where piece 0 is the solid piece. A total of 69 different level 1 standard 6-piece burrs can be selected, where all use piece 0 as a key piece, and the other 5 pieces are specified with a tic-tac-toe notation:
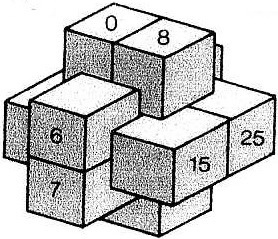


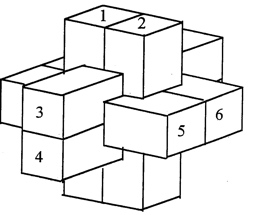
Made by Interlocking Puzzles 2000.
(7 x 6 x 3.4 inch Jarrah box with 42 Chechen pieces, each 3/4 x 3/4 x 2.4 inches)
25 distinct notchable 2 x 2 x 6.5 unit pieces, indexed from A to Y, a total of 42 pieces including duplicates, which can be used to assemble the 314 different level 1 six piece burrs that have no holes. The set comes with five puzzle cards and five solution clue cards that list the pieces in order from 1 to 6 according to where they belong in the diagram above. This set does not contain all possible notchable pieces; just has the pieces necessary (and enough copies) to make all 6-piece notchable burrs with no holes. Also, some higher level burrs can be constructed with this set; for example, L5 Notchable is OODXNL and Holey Astigmatism is TYLLUM. Note that because the pieces are more than 6 units long, there are some higher level burrs that don't quite work, but would if the pieces were exactly 6 units long.
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Puzzle number 305 is {D,G,N,O,P,Q}. The solution hint 305 lists the order {O, Q, P, D, G, N). Looking at the burr figure we can make the correspondence:With this correspondence, one can see from the figure where each piece goes in the solved puzzle (but not which way to flip or rotate it), and this can make it a fun, but still not too easy, to solve the puzzle. The trick for this one is to first see how the pieces must fit together when solved, and then realize that the only way to put it together is to put three together into one half, three together in the other half, and then slide the three halves together:
1 = O
2 = Q3 = P
4 = D5 = G
6 = N





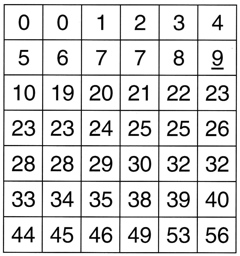
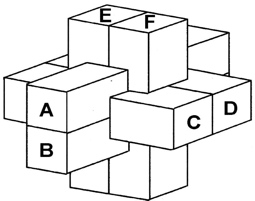
Made by Interlocking Puzzles 2000.
(6.6 x 5.75 x 3.2 inch wood box with 42 wood pieces, each 3/4 x 3/4 x 2.25 inches)
35 distinct notchable 2 x 2 x 6 unit pieces, indexed with numbers in the range 0 to 56 (as shown above), a total of 42 pieces including duplicates, which can be used to assemble most of the level 5 standard 6-piece burrs. Uses David Winkler's numbering. Four puzzle and clue cards that list the pieces in order from A to F according to the diagram above.
00
01
02
03
04
05
06
07
08
09
10
19
20
21
22
23
24
25
26
28
29
30
32
33
34
35
38
39
40
44
45
46
49
53
56

Assembling a cube shape from pieces is so common it merits its own category. Most of these puzzles leave you with a bag of pieces when unassembled, but a few, such as Hinged Cubes and Snake Cubes are manipulation puzzles where you can pick it up, play with it, and put it down unsolved to continue later.

Copyright 1966 Piet Hein,
produced in Denmark by Skj0de of Skjern for Parker brothers, No. 1050.
(4" box with wood pieces, metal base, and instruction booklet, 3.1" assembled)
Six of the 7 pieces are formed from 4 unit size cubes and the last piece isformed from 3 unit size cubes; the goal is to assemble them into a 3x3x3 cube. This is a relatively easy puzzle with many solutions. John Rausch credits the invention of this puzzle to Piet Hein in 1936.
Further reading:
Stewart Coffin's book, from: http://www.johnrausch.com/PuzzlingWorld/chap03a.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/soma/soma.htm
Johnson 1988 Patent, from: www.uspto.gov - patent no. 4,784,392
Johnson 1989 Patent, from: www.uspto.gov - patent no. 4,844,466


Designed by Stuart Coffin circa 1975, made by Cubic Dissection 2002.
(6 pieces, bocote, 2.25 inches square assembled)
Here is what Coffin says in The Puzzling World of Polyhedral Dissections:
"The six-piece version of the 3 x 3 x 3 cube will be considered first. For aesthetic reasons, one might prefer that all the pieces be the same size, but this is impossible, so the nearest approximation is to use three four-block pieces and three five-block pieces. It is also desirable that all pieces be non-symmetrical but this is likewise impossible so two of the four-block pieces will have an axis of symmetry. All pieces will of course be dissimilar. Of the several thousand such combinations possible the author tried several that proved to have either multiple solutions or no solution, until finally finding one with a unique solution."
Here is the solution hint that was sold with the puzzle:



Designed and made by Interlocking Puzzles circa 2001.
(5 pieces, 3 inches square assembled)
A similar theme, but not the same set of pieces as the 5 piece version of the 3x3x3 cube suggested by Stewart Coffin in Figure 55 of The Puzzling World of Polyhedral Dissections.


Designed by Stuart Coffin (circa 1975), Made by Interlocking Puzzles (circa 2001)
(4 pieces, 3 inches square assembled)
The photo on the right above shows the four pieces in their relative orientation for assembly. Here is what Coffin says in The Puzzling World of Polyhedral Dissections:
"With puzzles of this type, there are an optimum number of pieces; and as you tinker with them, you soon gain an intuitive sense of what that number is. There is no way that a four-piece version can be very difficult, although the one shown in Fig. 51 does have the intriguing property of being serially interlocking, meaning that it can be assembled in one order only. Is a five-piece serially interlocking version possible?"


Made by AussieStuff Puzzles, purchased from Mr. Puzzle Australia, 2006.
(13 pieces, wood, 6 inches)
Thirteen pieces, each designed from unit cubes, are assembled into a 4x4x4 cube; can also be assembled into a 4 x 16 rectangle. Here is the solution that was sold with the puzzle:

Purchased from UK3, 2006.
Here is a photo of the other three sides:


Purchased from Creative Craft House 2007.
(wood, 3.1 inches)
Named because the designer's wife commented that it would take a century to solve; here are the first few steps of dissassembly:






Designed by Stewart Coffin circa 1975, made by Interlocking Puzzles 2001.
(8 pieces, maple and bloodwood, 2 inches square assembled)
The wood used to make this puzzle gives a clue to the solution with symmetric color shown above; the photos below show three basic steps to this solution:



It is not unique, here are two views of another solution:


Stewart Coffin, in his book The Puzzling World of Polyhedral Dissections, describes the derivation of this puzzle as starting with all possible pairs of joined 1x2x2 blocks (where the resulting 10 pieces can be assembled into a 4x4x5 solid in 25 different ways) and then eliminate the two rectangular pieces (the 1x2x4 piece and the 2x2x2 piece) to see if the remaining 8 pieces can be assembled into a cube. He then goes on to say that they cannot be so assembled, but that one can be eliminated and one duplicated to make a set that can. He also notes "an interesting pattern of symmetry" in the solution.
The 1986 patent of Guenther describes puzzles where pieces are formed from pairs of rectangular solids.
Further reading:
Guenther Patent, from: www.uspto.gov - patent no. 4,534,563


"Just a Little Packing Problem #1",
made by Mr. Puzzle Australia, purchased 2006;
basic idea by Stewart Coffin circa 1975.
(8 pieces, Tasmanian Oak, 2 inches square assembled)
Like the Stewart Coffin Patio Block, puzzle, but with a slightly different set of pieces. The three photos below show basic solution steps:





Designed by Bill Cutler 1991, made by Cutler / McFarland / Peterson.
(wood, 2.5 inches)
Pieces formed from black and white unit cubes and half unit cubes (starred above) must be assembled to a 3x3x3 cube with a checkerboard pattern on all sides. The solution is unique and does not follow the checkerboard pattern in the hidden center.

Designed by V. Genel, sold by Puzzleman.com, circa 2000?
(Zebrawood and Walnut, 2+5/8 inches)
Four beautifully cut pieces come apart in pairs:



Designed by S. Coffin 1971, made by T. Lensch 2008.
(Marblewood and Brazilian Blackwood, 2.2 inches;
sold with a piece diagram piece diagram and an assembly diagram)
Described in Coffin's book, six identical pieces are augmented to make 6 different non-symmetric pieces, where two groups of three slide together diagonally:




Designed by Lee Krasnow, Pacific Puzzle Works, published August 29, 2018.
(Printed on a Monoprice Mini V1 3D printer, from Thingiverse thing 2975065, 2019,
PLA plastic, 1+7/8" square)
Three identical pieces slide together in a simultaneous symmetric motion to form a cube. Below on the left shows the other three faces of the assembled cube and on the right the pieces.


Further Reading
Slideways Thingiverse Page, from: http://www.thingiverse.com/thing:2975065
Slideways Metal, from: http://www.etsy.com/listing/617915791/slideways-cube?ref=shop_home_active_16


Design and Copyright by Hirokazu Iwasawa, 2003.
Left: 3D print design by Richard Gain, thingiverse no. 23279, 2012, 1.5" square.
Right: Crafted from walnut by Alex Storer, 2022, 2+5/8" square.
The puzzle can be assembled with a simultaneous motion in two dimensions on the surface of a table. Observe that there are two identical pieces and two identical mirror images of them. Arrange one of the pairs back to back. Then, holding the the other pair back to back and upside down, place them perpendicular to the other pair. The slide all four together together with a symmetric simultaneous motion.
Here are the steps of assembling a printed plastic puzzle listed as simply "Apparently Impossible Cube" at https://www.thingiverse.com/thing:23279; this one fabricated on a Monoprice V2 printer in 2021, PLA plastic, scale 120%, infill 22%, resolution 0.175mm:




Here are the steps of assembling the walnut puzzle (made by constructing a jig for making table saw cuts with a flat top blade):






Basic idea by Stewart Coffin, made by J. Storer 1989.
(purple heart with light wood dowels, 3 inches)
Stewart Coffin proposed this class of puzzle to make a 2x2x2 cube from 8 unit cubes, where each has three mutually perpendicular holes, and a total of 12 dowels are inserted into 12 of the 24 holes. He observed that the holes have one of two "reflexive forms", and that puzzles could be made by having all pieces of one form or having 4 with one and 4 with the other. The cubes of this puzzle all have the left form; the photos show basic solution steps:







Basic idea by Stewart Coffin, made by J. Storer 1989.
(top: purple heart with dowels, 3 inches;
bottom: rosewood with dowels, 2.25 inches)
Like the Cubes and Pegs puzzle, except here 4 pieces have one form and 4 the other (the pattern of pegs in the soluton to this puzzle is different from Coffin's Book Fig. 193):




Designed by Ronald Kint-Bruynseels, made by Eric Fuller 2007.
(walnut box and 9 cocobolo pieces with pegs, 2.5 inches)
Nine identical 3-unit L-shaped pieces with pegs added to assemble in a unique solution to a 3x3x3 cube. Here are basic solution steps:





Patented by Andy Turner, made by Eric Fuller 2010.
(Oak box 2.75" square by 2.1" high, Bubinga puzzle 2.2" square)
Don't read any further; have some fun first. This puzzle is quite hard until one sees the trick, and then it is almost impossible to forget how to solve it.
The two 1x2 pieces have double holes at one end that naturally entices one to use them, but in fact these two faces butt against each other in the unique solution (no pegs going between them), and then the puzzle solves easily. Here are four photos in sequence of assembly:






Designed Stewart Coffin, made byInterlocking Puzzles 2000.
(7 pieces, bloodwood and aluminum, 3 inches)
There are a total of 7 pieces; 2 pieces formed from 5 unit cubes with holes and rods, 4 pieces formed from 4 unit cubes with holes and rods, and one 3 unit long rod. They must be assembled into a 3x3x3 cube (there is a unit void in the center). Stewart Coffin proposed this class of puzzles and suggested this particular selection of pieces as one that has a "satisfactory" set of two solutions. Below are two stages of a solution for which the last piece placed before the rod is the T, and two stages of a solution for which the last piece placed before the rod is the Z:






Designed Stewart Coffin; left Interlocking Puzzles 2005, right Coffin circa 1980.
(left: mahogany, eight pieces, 3.25 inches,
right: mahogany, walnut, szjo, eight pieces, 2.75 inches;
right is one of 6 puzzles purchased during a visit with the designer in the early 1980's)
Featured in a December 1991 article in Fine Woodworking Magazine. Described in Stewart Coffin's book The Puzzling World of Polyhedral Dissections; here is some of what he says in the directions that came with the puzzle:"Special version - only one made. No half-pieces, so ignore puzzle problems that require half-pieces. The cube has only one solution in which all sides have matched wood and grain symmetry."The pieces are the eight ways to glue together a basic U-shaped piece; below are the pieces of the Interlocking puzzle version, the one made by Stewart Coffin pulled apart, and his grain pattern:



The wood and grain restriction has only one solution, but on the other hand, you are given clues how to do it. For example, there is just enough walnut to go around (a total of 8 squares), and so the solution cannot have any of the walnut squares hidden in the middle. For the single wood version, here is one of the solutions:




For the single wood version, Interlocking Puzzles said that there are 7 solutions each with a symmetric version; here is the solution sheet that was sold with the puzzle:
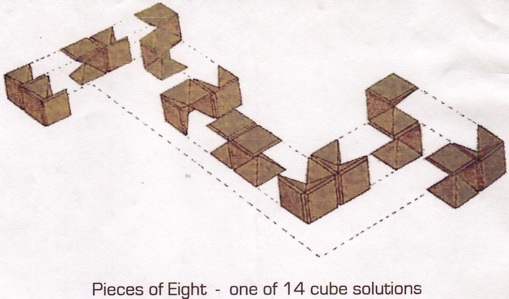


Designed Rick Eason 2004, purchased from Mr. Puzzle Australia 2006.
(Burdekin Plum, 2.4 inches)
The solution is unique and made more difficult due to 3 "false solutions" (arrangements that could exist in a solved state but there is no order of assembly to achieve any of them). Below are photos of two steps in the solution and the sheet that came with the puzzle:



Further reading:
Winter Patent, from: www.uspto.gov - patent no. 6,241,248


Designed by Rick Eason 2001, made by John Devost 2007.
(Bocote and Cherry, 4 pieces, 2.4 inches square;
as described on Rick Eason's Page, this puzzle was also mass produced as
"Confusion Puzzle Mental Block" shown on the right above - wood 2.9" square)
Four pieces formed from unit cubes and rods of dimensions 1/2 by 1/2 by 2.5 units.
The photos below show the four pieces positioned to be assembled, and pairs put together; the final step slides these two halves together to get the solved cube shown above.


Further Reading
Rick Eason's Page, from: http://www.mechanicalpuzzles.org/puzzles/index.html
Amazon: http://www.amazon.co.uk/Lagoon-CONFUSION-PUZZLE-MENTAL-BLOCK/dp/B004KYNB76

Designed by Kevin Holmes and Rik Van Grol, made by Eric Fuller 2009.
(Peruvian Walnut and Spalted Oak, 2.7 inches)
A beautiful and fun puzzle; here are photos of assembly:








Made by Takeyuki Endo, 1996.
(cardboard box, 14 oak pieces, direction / solution sheet, 2.75"square)
Four different types of pieces, each a flat piece connecting unit size cubes, which can be assembled in six different ways to solve to a cube.

Designed by Markku Vesala, made by Eric Fuller 2016.
(Purpleheart with nylon dowels, 3 inches square)
Here is what the puzzle maker said:"The 3x3x3 cube is pretty played out. With only 27 units there are only so many things you can do with it. That's assuming tradition block glued to blocks...if you open up edge connections, a whole new world of complexity appears! Markku's excellent Liberal Cube makes good use of these dynamics, with a very confusing and difficult seven piece serial assembly. I would estimate that the difficulty is on par with Coffin's Convolution design which of course uses a 4x4x4 design format. This puzzle is a lot of fun and displays very well with the contrasting white dowels against the dark purpleheart."Here are 6 photos (not to scale) of the puzzle coming apart:

a.k.a. Magic Cube
Circa 2000.
(laminated cardboard with Andy Warhol art, 2.75 inches)
Unlike the Hinged Cubes puzzle, this puzzle is trivial to solve and is more of a toy than a puzzle. The cube shown above, can be unfolded in two different ways to form a 2 x 4 array, and then in both cases that 2 x 4 array can be folded lengthwise to form another 2 x 4 array:








Copyright James A. Storer 2009; U.S. patent 8,393,623 March 2013.
(Kingwood with brass hinges, 2.25 inches square assembled)
Fold the eight cubes into a larger 2x2x2 cube; there are seven hinges:

Hinge 1 joins cube 2 to cube 1, on the front faces.
Hinge 2 joins cube 3 to cube 2, on the back face of 3 and the right face of 2.
Hinge 3 joins cube 4 to cube 3, on the top faces.
Hinge 4 joins cube 5 to cube 4, on the front faces.
Hinge 5 joins cube 6 to cube 5, on the left face of 6 and the right face of 5.
Hinge 6 joins cube 7 to cube 6, on the back face of 7 and the front face of 6.
Hinge 7 joins cube 8 to cube 6, on the top faces.
Fun but not too hard; people often spend 30 minutes or so to solve. Solid hinges suggest folding one cube at a time, which can lead to a position like the one shown on the right above.
Construction has four types of hinge cutouts:Type A: Cube 1,7,8: Top-RightThe types can be arranged in this order and then rotated appropriately to attach hinges:
Type B: Cube 2,5: Top-Right, Left-Up
Type C: Cube 3,4: Top-Right, Back-Up
Type D: Cube 6: Top-Right, Front-Up, Left-Right1 2 3 4 5 6 7 8
A B C C B D A A
A Full 3D Print of the Hinged Cubes
Made by J. A. Storer, 2022 (2.25" square assembled; a 2" version was also made).
Prints the 8 cubes and then attaches the same brass hinges used for the original wood version, where precise cutouts and screw holes are made for the hinges.




Made by Andrew Soshea, 2022 (2.25" square assembled).
This clever design prints a fully working puzzle. The hinge pins have a tolerance around then so that no cracking of joints is needed after printing. The box is a separate fully working 3D print; writing on the box top and bottom is via a thin initial layer before changing colors.



Kev's Cubes, sold by Trench Puzzles circa 1985,
this one made by J. Storer 1988.
(bloodwood, 2.8 inches assembled)
Twenty seven cubes are threaded together with an elastic cord. The cord either pass through a cube or turns a corner in one. They can be folded to a 3x3x3 cube by rotating adjacent cubes with respect to each other (where none of the cord shows). The basic idea of cubes connected by an elastic cord is described in the 1965 U.S. patent 3,222,072, of A. F. Dryer.
Kev's Cubes are a different pattern than ones shown the Dryer patent where the snake starts and ends in a face center, which can make the puzzle tricky given that it is natural for a triplet (three cubes in a row) that is at one end to start in a corner:




If the cube sequence was alternately colored black and white, then the solved 3x3x3 cube has black corners and face centers. The Kev solution is unique where the ends are face centers (unlike Cubra Cubes where ends are corners).
With the standard corded version, a cube can rotate in place due to the cord stretch. This 3D print version eliminates the cord and requires mechanical rotation of adjacent faces. One often needs to pre-rotate upcoming attached portions before a fold, thus precluding strictly sequential folding, and making it harder to visualize and quickly try out possibilities.
Referring to the figures on the preceding page, is convenient to solve by first positioning the three triples 25/26/27, 21/22/23, 19/20/21 and then working back to Cube 1. Cube 25 is the "Start Cube" (S), Cube 1 is the "End Cube" (E), "Bend Cubes" (B) turn the cord 90 degrees, and "Pass Cubes" (P) sends the cord straight through.
Cubes ordering can be represented as a character string broken up into the places where a P occurs and there are three cubes in a line (3 characters at the start and two places where 5 characters make a pair of them) to make substrings of lengths 3, 1, 5, 11, 5, 2:

The parts, based on 7/8" cubes, are Start, Bend, Pass, End, Peg, Plug:






Pegs are pushed in as far as they will go (hole depth allows the head to protrude appropriately). A cube is attached by sliding its peg head into the slot of the adjacent cube and inserting a plug. Although glue could be used, tolerances are sufficiently tight for puzzle play. The tolerance of the peg heads allows a cube to spin freely (so long it is against a flat plane of cubes).
On the left below, the decorative version uses a second color for the plugs. On the right below, the solid color version uses a different print for the bend cube that hides the plugs; for the 5 pass cubes and the end cube the same color plug is used (and for the solved puzzle the 6 exposed plugs can be hidden by appropriately rotating those cubes).




Plastic, 2+5/8" square when assembled, copyright J.A. Storer, 2023.




Cubra Cubes, purchased circa early 2000's.
(wood with elastic cord, both red and green versions, 2 inches square)


Exercise Your Brain, made in China, purchased 2024.
(wood cubes connected with elastic cord, with a solution sheet, 3 inches assembled)
The Cubra Cubes have been made in a number of patterns; the puzzles shown above are the first pattern shown in blue on Mark Weston's Page. Unlike Kev's Cubes, solution starts and ends in corners, and is not unique:"A solution can be described by a string of "directions" that the cube follows when you wrap it into a cube, either Right, Left, Up, Down, Forward, or Back. So for example if a solution starts R R F L ... then put the end of the snake with the rest trailing off to the Right, then the next cube goes in the same direction (it must be a straight-through cube), the next cube (a corner cube) turns to point Forward, then it goes Left, etc."
Solutions:
R R F L U U F D D R U B B L L F D F U U B B R R F F
R R U L F F U B B R F D D L L U B U F F D D R R U U

We show the solution with the Exercise Your Brain puzzle that has has larger cubes.
Because there are 9 triplets (as compared to only 4 in Kev's Cubes), solving can be thought of as how to pack them.
As shown below, starting from the right end of the sequence as pictured above, the ways the four triplets can be configured is quite limited; choose the one that makes a U-shape with the first 3 triplets, then the next two triplets must fold in, then the next two triplets must go together into the U, and the final triplet on an edge:




Here are photos of solving the puzzle in the opposite direction as the preceding page, where the four triplets are the last to fold on:








Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/snakecube.htm
Mark Weston's Page, from: http://www.cs.uvic.ca/~mweston/snakes.html
Eryk Vershen's Page; from: http://cantaforda.com/cfcl/eryk/puzzles/chain_cube.html
Dreyer Patent, from: www.uspto.gov - patent no. 3,222,072

Designed by Geoge Hart, published 2017.
(Printed on a Monoprice Mini V1 3D printer, from Thingiverse thing 2132796, 2019,
PLA plastic, 2" square)
Two pieces flow together to form a cube:

Further Reading
Helix Cube Thingiverse Page, from: http://www.thingiverse.com/thing:2132796

Packing puzzles typically require one to fit pieces into a tray (two dimensional) or a box (three dimensional), although sometimes the problem is to fit the pieces into a particular shape. Perhaps the most well known example, which as been around for centuries, is the tangram, where the goal is to use the same set of simple two dimensional shapes to make many different shapes.
a.k.a. All Square Novelty Puzzle, Check-A-Board, Tyr & Do It,




Famous Checkerboard Puzzle, Weekly Telegraph Chessboard Puzzle
Left: Made 1940's by a relative of J. A. Storer who lived in up-state New York.
(wood cigar box and painted pieces cut from 1/4" masonite, with 1" squares)
Right two: J. F. Friedel Co., Syracuse, N.Y, circa 1940's.
(6.5 by 8 by 1" cardboard box and 12 cardboard pieces with 1+3/8" squares;
top edge says "Mfg. by J. F. FREDEL CO. Syracuse N.Y.";
bottom edge says "MFGS. REPRESENTATIVES POTTER & REAGAN")
Arrange the pieces to make a standard 8 by 8 checkerboard. There are 10 distinct pieces and two of the 5-unit Z's. Shown on pages 70-73 of the Haubrich book, which lists a unique solution (shown above). Here is another version made in Great Britian:


All Square Novelty Puzzle, Frederick Warne & Co.,
London and NY, circa 1930's?
(6.25 x 6.25 x 13/16 inch cardboard box
and 12 wood pieces based on 15/16" squares 1/8 inch thick;
directions on the back of the box)
Note: Frederick Warne & Co. is the publisher of
the 1893 Hoffmann book.



Patented by H. Luers and made by Selchow & Righter, NY, circa 1880.
(8.5 inches square by 3/4 inch cardboard box and 15 cardboard pieces, 14 distinct;
pieces based on 1 inch squares can be arranged in the box;
on the cover and pages 217-219 of the Haubrich book,
which lists this puzzle having 6,013 solutions;
solution on the left above is from Haubrich, and right is from the Luers patent)
Left is a solution a previous owner drew inside the box bottom, right is the label on the box top, and below is the label inside the box top.



This version is nearly identical to the one shown on the previous pages, except the color of the label on the box top is a bit more brown than gray, and the pattern around the edge is a bit different (and this one has nothing inside the box top or bottom).





Phenyo-Caffein Co., Worcester, MA, circa 1900.
(5.25 inches square by 5/8 inch cardboard box and 15 cardboard pieces, 14 distinct;
pieces based on 5/8 inch squares can be arranged in the box;
also made with a wood box of the same dimensons and graphics)
The Pheno-Caffein Co. also made the Misfit 6 Piece Burr. The inside of the box bottom (on the right above) challenges the solver by stating that the dark square of the smallest piece can occupy any of the 32 dark squares. The sheet available from the company, on the next page, shows eight solutions (representing solution classes).

Further Reading
Luers Patent, from: www.uspto.gov - patent no. 231,963






a.k.a. Famous 'Bug House' Puzzle
Feltham Co., London, Royal Letters Patent 16,310, circa 1889.
(cardboard box and 14 thick cardboard pieces, 5" x 5" x 1/2";
box bottom has add for Feltham's tennis bat;
has a sheet that is the same as what is on the inside of the box bottom;
shown on pages 165-174 of the Haubrich book,
which gives the date and lists this puzzle as having 84 solutions; one is shown above)

Franco, NY, circa 1948.
(cardboard box and 14 distinct metal pieces, 3.25" x 3.25" x 1/2")

The Bug House Puzzle, E.I.H. Co. and F&K, 1912.
(cardboard box and 14 distinct metal pieces, 2.1 by 3.1 by 1/2 inches;
inside box top gives directions and manufacture;
shown on the cover and on pages 150-151 of the Haubrich book,
which gives the manufacture date,
identifies "E. I. Horsman Co." and "Forsheim & Koningsberg", NY,
and lists this puzzle as having 141 solutions, one of which is shown below)


Note: There were a number of variations of this puzzle made. This one is the same as page 150-151 of the Haubrich book if the pieces with dots in the photo above are taken to be black; however, the dots shown in the Haubrich book are not in the same locations.




Vasen Mfg. Co., Davenport, Iowa, 1928.
(cardboard box and 14 distinct cardboard pieces, 4.25 by 4.25 by 5/8 inches;
inside box bottom says you can send 10 cents to get three different solutions;
shown on pages 158-164 of the Haubrich book,
which lists this puzzle as having 84 solutions, one of which is shown above)
Note: Pages 165-174 of the Haubrich book show puzzles that are the same except for the colors reversed, and pages 183-187 of the Haubrich book include the same box top where if the pieces for those puzzles have the colors reversed, they are the same except for one (and the same as Xcel Checkerboard Puzzle No. 1).

Doyle Puzzle Co., Buffalo, NY, circa 1920?
(cardboard box 5.1"x5.1"x7/8", and 14 distinct cardboard pieces with 3/4" squares;
same as the Famous and Baffling Checkerboard Puzzle with colors reversed;
also made in a 13 piece version, the New XceL Checkerboard Puzzle No. 2;
shown on pages 183-187 of the Haubrich book,
which lists this puzzle as having 84 solutions, one of which is shown below)

Note: The Chequers Puzzle shown on page 97 of the 1893 Hoffmann Book is the same as a mirror image of this puzzle, except that puzzle shows only 63 squares, and can be corrected to make one of the three 4-unit L's be a 5-unit Z.

Doyle Puzzle Co., Buffalo, NY, circa 1920?
(cardboard box 5.1"x5.1"x7/8", and 13 distinct cardboard pieces with 3/4" squares;
also made in a 14 piece version, the XceL Checkerboard Puzzle No. 1;
shown on page 122 of the Haubrich book,
which lists this puzzle as having 7 solutions,
5 of which a composed of two 4 by 8 solutions,
one of these 5 and one other are shown below,
where the black squares correspond to green and the white to black)



Gyro Checker Board Jig Saw Puzzle, undated.
(3.5 by 6 inch envelope and 14 distinct cardboard pieces based on 1 inch squares;
shown on page 196 of the Haubrich book,
which lists this puzzle as having 598 solutions, one of which is shown below)



a.k.a. Krazee Checkerboard Puzzle, Zebas Puzzle,
Banzee Island Checkerboard Puzzle, 59-444 Checkerboard Puzzle
Peter Pan Playthings, England, circa 1950.
(plastic box and 12 plastic pieces, 4.75 by 4 by 5/16 inches;
there are 11 distinct pieces, where there are two of the 6-unit L;
shown on pages 57-65 of the Haubrich book, which gives the manufacture date
and list this puzzle as having 11 solutions, one of which is shown above;
pages 60-65 show reflected with reverse colors patented by J. Avila-Valdez 1995)
Arrange the pieces to make a standard 8 by 8 checkerboard. Paper, shown below, is glued to the bottom inside of the box that gives a layout for quickly storing the pieces unsolved in the box. The bottom of the box is a non-transparent black plastic that does not allow you to see the back of the paper. However, by holding it up to the light one can see that the reverse side of the paper has instructions similar to the Krazee Checkerboard Puzzle, shown on the following page.

Further Reading
Avila-Valdez Patent, from: www.uspto.gov - patent no. 5,403,005




Krazee Checkerboard Puzzle, Plas-Trix Co., Jamica, NY, 1957.
(plastic box and 12 plastic pieces, 4.75 by 4 by 5/16 inches;
same puzzle as the Draught Checkerboard Puzzle shown on the previous page,
but the back of the box is clear to allow one to view directions;
also shown on pages 57-58 of the Haubrich book, which gives the manufacture date)

Zebas Checkerboard Puzzle, Plas-Trix Co., Brooklyn, NY.
(plastic box and 12 plastic pieces, 4.75 by 4 by 5/16 inches;
same puzzle as the Krazee Checkerboard Puzzle shown on the previous page,
and also made by the Plas-Trix Co., but with different packaging)


Banzee Island Checkerboard Puzzle, made in Hong Kong.
(12 plastic pieces in plastic bag with cardboard top, 6.25 by 6.5 inches;
same puzzle as the Zebas Checkerboard Puzzle shown above,
the back of the package top refers to Chief Zebas)


S. Adams Co. Neptune, NJ., Copyright 1958.
(6" by 4" cardboard package and six 3.5 by 2.5 inch puzzles,
the checkerboard and five others, including Magic T;
shown on page 167 of the Adams Co. History book;
shown on page 21 of the Haubrich book.
which presents the unique solution shown above)




Made in Japan circa 1940.
(wood box 3.8 by 3.75 by 7/16 inches thick and 19 wood pieces;
wood inlays on the box cover are 5/8 inch diameter;
paper stamp on the back is 1/2 inch square)
Purchased from someone who remembered it from his childhood in the 1940's. At some point in the past the following solution was drawn:


This puzzle has the same dimensions, style, and cover inlays as the 16 piece puzzle on page 233 of the Haubrich book. However, even if one assumes that the 1x1 pieces broke off of larger ones before the solution above was drawn, and taking into account rotations and reflections (the pieces are double sided), there is no way to make it the same (and no way to further combine pieces to make it the same as the 14 piece puzzle of the same style on page 177) Here are the 16 pieces if the 1x1's are joined to the pieces above them in the solution above:

a.k.a. Caricature, Cut-Up Square, Stone Tangram,



Union Stone Puzzle, Richter Anchor Stone Puzzle No. 8
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3.1" x 3.1" x 9/16", 7 stone pieces, booklet, and solution booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1890;
described on pages 77-79, 96-97, 111-115, 128 of the 1893 Hoffmann book.
"casse tete" and "kopfzerbrecher" mean headache in French and German;
inside of the cover shows how to pack the pieces into the box;
inside of the box bottom has an add for "Dr. Richter's Pain-Expeller";
booklet has multi-language text inside covers and on pages A to Q at the front,
and 64 pages with 195 shapes to make,
where the last 16 pages are shapes made in combination with another puzzle;
second booklet has solutions)
An old design known as the Tangram, dating back to ancient China; seven tiles, called Tans, can be used to make different shapes. The Richter Company of Germany, known for stone building blocks, started making this puzzle and others in 1891. It is number 8 of over 36; see The Anchor Puzzle Book, The Tangram Book, Slocum and Botermans books, and also the Richter Summary later in these pages. Many versions of the tangram have been made, some packaged as two squares of half the area:

Richter (1846-1910) had a number of business besides stone building sets and puzzles, including selling medicines (see the Richter history on the Ankerstein Page). Many of the Richter puzzles have adds or testimonials to his pain medicine. The add below is on the inside of the box bottom of the puzzle on the preceding page.

The text on pages A to Q at the start of the booklet that precedes the 64 pages of shapes is very similar to that in versions of a number of other Richter puzzles (e.g., see the corresponding pages for the Tormentor and Pythagoras puzzles). Page L describes how the last 16 pages are shapes made in combination with another puzzle; shapes 180 to 183 use the Circular Puzzle, shapes 184 to 187 use the Tormentor, shapes 188 to 191 use the Cross Puzzle, and shapes 192 to 195 use Pythagoras. An English description similar to what is on Page L is given in the description that came with the "Puzzle Drive" version shown below.
































Note: These pages are shown in order (left to right, top to bottom), except that page 64 (pattern 195) is shown with page 1 (patterns 1 through 4).
This figure was extracted from the page scans shown on the preceding page; the patterns are in the order as in the booklet (left to right, top to bottom), except that page 64 (shape 195) is shown with page 1 (shapes 1 through 4).

The shapes on the first 48 pages need only the pieces of this puzzle. This figure was cropped from the figure of all shapes on the preceding page; the patterns are in the order as in the booklet (left to right, top to bottom), except that the last 4 patterns (page 48) are at the end of row 1.




(cardboard box 3.2 by 3.2 by 5/8 inches, 7 stone pieces, and two booklets;
the inside of the cover shows how to pack the pieces into the box;
box is constructed with a lip on the bottom,
booklet cover says "The Anchor Puzzle 3rd Ed",
booklet inside cover for "Casse-Tete Persan" and cover for "Kopfzerbrecher",
which says that this is the "third edition" at a price of "15 kr.",
is followed by a 3 page French and German introduction,
followed by unnumbered pages of shapes similar to the puzzle on the first page,
followed by a final page, in German, that advertizes Anchor blocks
by referring to the picture on the back of the booklet;
second booklet is a work book with shapes to draw in and many blank pages)



(cardboard box 3 by 3 by 9/16 inches, 7 stone pieces, and two booklets;
similar to the version on the previous page;
a more compact box where the small bottom lip is hidden when the cover is on;
box top graphics and booklet front and back (shown above) are the same;
inside box bottom advertizes "ANCHOR PAIN EXPELLER" from 1890;
booklet is basically the same except it is in German and English;
booklet inside cover for for "Kopfzerbrecher" and "The Anchor Puzzle",
which says that this is the "third edition" at a price of "10 cents",
followed by a 3 page German and English introduction,
followed by unnumbered pages of shapes similar to the puzzle on the first page,
folloed by a final page, in English, that advertizes Anchor blocks
by refering to the picture on the back of the booklet)





(cardboard box 3.1 by 3.1 by 1/2 inches, 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
box bottom lists other puzzles for sale,
the booklet has 64 pages of the same 195 shapes as the puzzle on the first page,
along with the single loose double sided page of English directions shown above)
some versions have the same box cover with "UNION" instead of "ANCHOR"
and the same booklet cover with just "STONE PUZZLE" on a single line)





(cardboard box 3.1 by 3.1 by 5/8 inches, 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
box and booklet front show copyright, and booklet back shows the U.S. manufacturer;
the booklet has text on the insides of the covers and 48 pages
of the same 179 shapes as the first 48 pages of shapes on the first page;
unlike earlier versions of this puzzle, an explicit copyright date is shown)


(cardboard box 3.1 by 3.1 by 9/16 inches, 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
the booklet has 64 pages of the same 195 shapes as the puzzle on the first page,
however its cover is blank, and there is no text explaining that
the last 16 pages are shapes made in combination with another puzzle;
the pages of this booklet were used for the scans shown earlier)


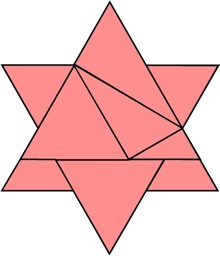
a.k.a. All Nine, Richter Anchor Stone Puzzle No. 1
F. Ad. Richter & Co., Germany, late 1890's / early 1900's
(cardboard box 2.7" x 4.4" x 1/2", 9 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1899;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 141 shapes to make,
the first of which is the star, which can be solved as shown above,
and where the last 16 pages are shapes made in combination with another puzzle)



(cardboard box 2.7" x 4.4" x 1/2", 9 stone pieces, and booklet;
booklet has the same shape pages as the one on the previous page,
but no additional text pages;
back of the box lists other puzzles)


a.k.a. Richter Anchor Stone Puzzle No. 2
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3.1" x 3.6" x 9/16", 7 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1893;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 140 shapes to make;
where the last 16 pages are shapes made in combination with another puzzle;
the first four shapes are the rectangle, parallogram, triangle, and hexagon)


Same size box and booklet as version on the preceding page.
The booklet starts with 16 not numbered pages, where the first 12 are a page of directions in 12 different languages, and the last 4 pages have multi-language text with a coupon that could be mailed in along with 15 cents to get solutions to all of the problems. Following these 16 pages are 48 pages of the same problems as the version on the preceding page. The booklet front cover, inside of the front cover, inside of the back cover, and the back, present the same text in 12 different languages; on the inside of the back cover, the English text says "Second book to The "Lightning Conductor" for drawing in the lines of solved problems." So it would appear to be the second of two booklets that originally came with the puzzle.


Same size box and booklet as version on the preceding pages.
The booklet has 48 pages of the same problems as the version on the preceding pages.



(cardboard box 3.1" x 3.7" x 1/2", 7 stone pieces, and booklet;
German text on inside of front and back cover;
also has a loose sheet with directions in German;
same 48 pages with 140 shapes to make as puzzle on first page)
(same pieces but different shapes than Richter 16 Magic Egg)



a.k.a. a.k.a. Columbus' Egg, Columbian Puzzle, Richter Anchor Stone Puzzle No. 3
Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.1" x 4.1" x 9/16" with wood inserts, 9 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1893;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 111 shapes to make,
where the last 16 pages are shapes made in combination with another puzzle;
there are no graphics on the back of the booklet)



(cardboard box 3.1" x 4.1" x 1/2" with wood inserts, 9 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
the booklet has multi-language text inside the covers and on pages A to Q at the front,
and 32 pages with 95 shapes to make;
the booklet is the same as the one on the preceding page
except without the final 16 pages)




(cardboard box 4" x 3.5" x 5/8" with cardboard insert, 9 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
booklet has Spanish and Hungarian inside the front cover and German inside the back cover,
and at the front are 3 pages of Spanish directions and 4 pages of Hungarian directions,
48 pages present the same pages as the puzzle on the first page,
where the figures have a shaded green texture as shown above)


a.k.a. Richter Anchor Stone Puzzle No. 4
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 4.1" x 3.1" x 9/16", 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1896;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 130 shapes to make,
where the directions state that the first is the square using only 6 pieces,
the second is the right triangle of 3/2 the height of the square using only 7 pieces,
all others use all eight pieces,
and where the last 16 pages are shapes made in combination with another puzzle)


(cardboard box 3.1" x 4.1" x 1/2", 8 stone pieces, and booklet;
similar booklet with the same shapes as the version on the previous page)




(cardboard box 3.25" x 4.1" x 9/16", 8 stone pieces, and booklet;
same problem pages as the versions on the preceding pages,
but with no front or back matter, except for a loose double sided page
tucked under the cover - front and back shown above)


a.k.a. Richter Anchor Stone Puzzle No. 5
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3" x 3.6" x 9/16", 7 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1893;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 108 shapes to make,
where the last 16 pages are shapes made in combination with another puzzle)



(cardboard box 3" x 3.6" x 9/16", 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text on pages A to Q at the front,
and 48 pages with the same 108 shapes to make as the puzzle on the preceding page)


(cardboard box 3" x 3.6" x 9/16", 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
this one is missing the booklet;
it came with some extra cardboard pieces
that are in the bottom of the box below the stone pieces)




(cardboard box 3" x 3.6" x 9/16", 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
booklet has 48 pages with the same 108 shapes to make as the preceding pages)




a.k.a. Richter Anchor Stone Puzzle No. 6
F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 3.5" x 3.5" x 9/16", 9 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1911;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 32 pages with 98 shapes to make;
the text above is on the box bottom under the puzzle)





Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.5" x 3.5" x 9/16", 9 stone pieces, and booklet;
booklet has the same 32 pages with 98 shapes to make
as the puzzle of the first page, but no additional text;
included is one loose double sided page of text)


a.k.a. Goblin, Richter Anchor Stone Puzzle No. 7
F. Ad. Richter & Co., Germany, late 1890's / early 1900's
(cardboard box 3" x 4" x 9/16", 7 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1899;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 143 shapes to make;
where the last 16 pages are shapes made in combination with another puzzle;
a previous owner has penceled in a solution to the first problem shown above)


(cardboard box 3" x 4" x 9/16", 7 stone pieces, and booklet)
The inside of the cover shows how to pack the pieces into the box;
booklet shows the same shapes as the puzzle on the previous page,
but includes no text.


a.k.a. Richter Anchor Stone Puzzle No. 9
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3.6" x 3.6" x 9/16", 10 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1891;
described on pages 85-87, 120-121 of the 1893 Hoffmann book;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 121 shapes to make;
where the last 16 pages are shapes made in combination with another puzzle)



Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.6" x 3.6" x 9/16", 10 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
the booklet starts with 8 pages of multi-language text,
followed by 48 pages of the same 121 shapes as the puzzle on the first page;
this box top was made with a number of variations a b of the text for different markets)





Richter Co., circa 1890's / early 1900's.
(cardboard box 3.7" x 3.7" x 9/16", 10 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
box bottom lists other puzzles for sale,
booklet has 48 pages of the same 121 shapes as the puzzle on the first page,
along with the single loose double sided page of English directions shown above)

a.k.a. Sherlock Holmes, Hi Ho, Richter Anchor Stone Puzzle No. 10





F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3" x 3.75" x 9/16", 7 stone pieces, and two booklets;
the Anchor Puzzle Book dates this puzzle as first made in 1892;
described on page 83-85, 118-119 of the Hoffmann book;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the inside of the bottom has a testimonial dated 1899,
variations of this testimonial appear in the box top or bottom other versions;
first booklet has multi-language text inside covers and on pages A to Q at the front,
and 48 pages with 149 shapes to make
the first of which is the cross as shown above,
and where the last 16 pages are shapes made in combination with another puzzle;
the second booklet gives a solution for each shape)



Same dimensions as version on the first page;
the inside of the cover shows how to pack the pieces into the box;
booklet has nothing on the inside covers,
with 8 unnumbered pages of multi-language text,
followed by the same 48 pages of problems as the version on the first page;
the first page credits Dr. Richter's Publishing House, 215 Pearl St., NY;
second booklet is the same solution booklet as the one on the first page.



Same dimensions as version on the first page;


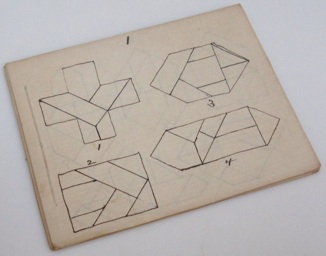

box construction uses a lip on the bottom;
the inside of the cover shows how to pack the pieces into the box;
inside of the bottom has a testimonial dated 1890;
inside covers and first 8 unnumbered pages have multi-language text,
followed by 48 pages with the same problems as the version on the first page;
however, the problems are drawn with black line art rather than red coloring;
the first page of problems is shown to the right of the booklet cover above;
second booklet has solutions for problems on the first 32 pages.
Note: Version shown on the top right is Dutch version; it says "Kruisraadsel" at the bottom of the box top and on the front cover of the booklet (which has the identical pages).


Same puzzle as the one shown on the first page;
3" x 3.7" x 1/2";
booklet has the same 48 shapes to make,
but without the text pages at the front and back.


a.k.a. Richter Anchor Stone Puzzle No. 11
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3.1" x 3.1" x 5/8", 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1894;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has 8 pages of multi-language text at the beginning,
and 32 pages with 89 shapes to make)



Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.1" x 3.1" x 9/16", 8 stone pieces,
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside covers and on pages A to Q at the front,
and 32 pages with 89 shapes to make, same as those on the preceding page)


Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.1" x 3.1" x 5/8", 8 stone pieces,
and booklet of 32 pages with the same 89 shapes as the preceding page)



a.k.a. a.k.a. Richter Anchor Stone Puzzle No. 12
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3 by 3 by 9/16 inches, 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1891;
described on pages 81-83, 117-118 of the 1893 Hoffmann book;
similar in construction to the Anchor Puzzle Tangram;
the inside of the box cover shows how to pack the pieces into the box;
the inside of the box bottom has a testimonial dated 1899;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 64 pages of 197 shapes to make,
where the last 16 pages are shapes made in combination with another puzzle)
Described on page L of the booklet, the last 16 pages are shapes made in combination with another puzzle; shapes 182 to 185 use the Anchor Puzzle, shapes 186 to 189 use the Tormentor, shapes 190 to 193 use the Circular Puzzle, and shapes 194 to 197 use the Cross Puzzle.
































Note: These pages are shown in order (left to right, top to bottom), except that page 64 (pattern 197) is shown with page 1 (patterns 1 through 3).
Here are the front and back cover, the inside front cover, pages A through Q that come before the problem pages, and the inside back cover. The text in German, French, and English discusses this and other puzzles, and gives testimony from a satisfied customer.















Similar to the version on the first page, but
box has different construction with a lip on the bottom,
booklet has multi-language text on inside covers and 6 unnumbered pages,
and the booklet has the same problems but drawn with black and white art
(first three pages of problems shown above)




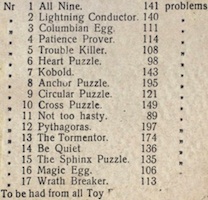
Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.1 by 3.1 by 1/2 inches, 8 stone pieces, and booklet;
the inside of the box cover shows how to pack the pieces into the box;
the booklet has the same 64 pages with 197 shapes to make as the puzzle on the first page,
where the last 16 pages are shapes made in combination with another puzzle,
and the extra double-sided sheet describes them)



Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3 by 3 by 1/2 inches, 8 stone pieces, and booklet;
the cover slides on;
the booklet is 48 pages of 181 puzzles;
these 48 pages are the same as the first 48 pages of the puzzle on the first page;
there is an extra double-sided text page in German between pages 18 and 19,
that seems to be a bit out of place because it discusses
the combinations that would be on the other 16 pages)



a.k.a. Richter Anchor Stone Puzzle 13
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3 by 3 by 9/16 inches, 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1891;
described on pages 80-81 of the 1893 Hoffmann book;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the inside of the bottom has a testimonial dated 1899;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 64 pages with 174 shapes to make,
where the last 16 pages are shapes made in combination with another puzzle)
Described on page L of the booklet, the last 16 pages are shapes made in combination with another puzzle; shapes 159 to 162 use the Circular Puzzle, shapes 163 to 166 use the Anchor Puzzle, shapes 167 to 170 use the Cross Puzzle, and shapes 171 to 174 use Pythagoras.
































Note: These pages are shown in order (left to right, top to bottom), except that page 64 (pattern 174) is shown with page 1 (patterns 1 through 4).
Here are the front and back cover, the inside front cover, pages A through Q that come before the problem pages, and the inside back cover. The text in German, French, and English discusses this and other puzzles, and gives testimony from a satisfied customer.












Same as the version on the first page
except for the art on the box top and the front and back of the booklet
(same box top inside, testimonial, booklet text and problems).





Similar to the version above, but
box has different construction with a lip on the bottom,
booklet has multi-language text on inside covers and 8 unnumbered pages,
and the booklet has the same problems but drawn with black and white art;
the first three pages of problems are shown above.




(cardboard box 3.1 by 3.1 by 1/2 inches, 8 stone pieces, and booklet;
inside of the box cover shows how to pack the pieces into the box;
booklet has the same 64 pages with 174 shapes as the puzzle shown on the first page,
where the two sided instruction sheet describes the puzzle)



a.k.a. Richter Anchor Stone Puzzle No. 14 (sometimes 3)
F. Ad. Richter & Co., Germany, late 1890's / early 1900's
(cardboard box 3" x 3+7/8" x 1/2", 10 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1899;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has 48 pages with 136 shapes to make,
where the last 16 pages are shapes made in combination with another puzzle;
the solution to the first problem in the booklet is shown above)
Note: Although usually referred to with the number 14, some versions of the box graphics showed the number 3.


a.k.a. Richter Anchor Stone Puzzle No. 14 /3
Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3" x 3+78" x 1/2", 10 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
booklet has 48 pages with the same 136 shapes to make as the preceding page)


a.k.a. Richter Anchor Stone Puzzle No. 14 /3
Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3" x 3+78" x 1/2", 10 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
booklet has 48 pages with the same 136 shapes to make as the preceding pages)

a.k.a. Lott's Stone Puzzle, Anchor Puzzle No. 15 (sometimes 16)

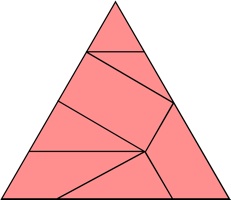

F. Ad. Richter & Co., Germany, late 1890's / early 1900's
(cardboard box 2.7" x 4.4" x 9/16", 7 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1899;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
a second way of packing the pieces into the box is shown by the figure above;
the inside of the bottom has a testimonial dated 1899;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 135 shapes to make,
the first of which is the pyramid of square root 3 times the height of the rectangle,
and where the last 16 pages are shapes made in combination with another puzzle;
Note: The box above does not show a number. However this puzzle was commonly listed by in Richter literature as number 15, and 15 appears on the boxes of some versions. It was also made with a box that has the same graphics as the one above with "No. 16." above the word Sphinx.




Puzzle pieces the same as the first page but box is 2.75" x 4.9" x 1/2";
booklet has the same 48 pages of problems but no additional text;
the inside of the cover shows how to pack the pieces into the box;
directions are on a separate two sided sheet that is slightly smaller than booklet pages.




Puzzle pieces the same as the first page;
booklet has the same 48 pages of problems but no additional text;
the inside of the cover shows how to pack the pieces into the box;
directions are on a separate two sided sheet that is slightly smaller than booklet pages.


"Lott's Stone Puzzle", copyright 1911, Lott's Bricks, LTD, Watford, England.
(cardboard box 2.7" x 4.2" x 9/16", 7 stone pieces, and booklet;
the booklet pages 1 and 2 are an introduction,
the last page invites one to write for a solution to another puzzle,
and pages 3 through 31 show 105 shapes to make,
where page 31 shows the rectangle for how to pack the pieces into the box)
(same pieces but different shapes than Richter 3 Egg Of Columbus)


a.k.a. Miracle Egg, Richter Anchor Stone Puzzle No. 16 (sometimes 17)
F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 3.1" x 4.1" x 9/16" with wood inserts, 9 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1912;
booklet has 48 pages with the same 106 shapes to make
as the puzzle on the following page, but without the other pages of text)



Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.1" x 4.1" x 9/16" with wood inserts, 9 stone pieces, and booklet;
also made with the similar box top but without "No. 17",
the inside of the cover shows how to pack the pieces into the box;
the booklet has multi-language text inside the covers and on pages A to Y at the front,
and 48 pages with the same 106 shapes to make as puzzle in preceding page;
the first page of shapes has written "Copyright Nachdruck verboten";
all shapes use only the 9 pieces of the puzzle;
the booklet names each shape in pages A to Y)


a.k.a. Richter Anchor Puzzle No. 17
F. Ad. Richter & Co., Germany, 1890's / early 1900's
(cardboard box 3.5" x 3.5" x 9/16", 7 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1893;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside the covers and on pages A to Q at the front,
and 48 pages with 113 shapes to make,
where the last 16 pages are shapes made in combination with another puzzle)



Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.5" x 3.5" x 9/16", 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text on eight unumbered pages at the front,
and 48 pages with the same 113 shapes to make as the puzzle on the previous page,
where the last 16 pages are shapes made in combination with another puzzle;
this Gnome theme box top was made with different variations of the text)


Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.5" x 3.5" x 9/16", 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
the booklet has the same 48 pages with 113 shapes to make
as the puzzle on the first page, but with no additional directions)




Richter & Co., Germany, circa 1890's / early 1900's.
(cardboard box 3.5" x 3.5" x 9/16", 7 stone pieces, and booklet;
the inside of the cover shows how to pack the pieces into the box;
the booklet has the same 48 pages with 113 shapes to make
as the puzzle on the first page, but with no additional directions);
two addition directions sheets are included)
Archimedes


F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 3.2" x 4.3" x 9/16", 9 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
booklet has multi-language text inside covers and on pages I to XIX at front,
where none of the text is in English,
followed by a blank page where a previous owner has drawn
a solution to the additional shape shown above,
followed by 32 pages with 97 shapes to make)
Bose Siben (Nasty Seven)



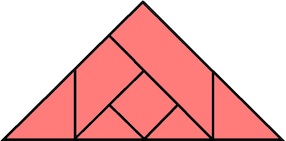


F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 2.25" x 4.25" x 1/2", 7 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has English text on the inside of the covers shown above,
and 32 pages with 99 shapes to make,
where the first is the rectangle for the box packing
and next three are the parallelogram, square, and triangle shown above)
Ritze Ratze (Razzle Dazzle)





F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 2.75" x 3.7" x 1/2", 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has English text on the inside of the covers shown above,
and 32 pages with 98 shapes to make,
where the first is the rectangle for the box packing
and the second is the parallelogram shown above)
Frisch Gewagt (Have Courage)





F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 2+11/16" x 4.25" x 1/2", 9 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has English text on the inside of the covers shown above,
and 32 pages with 96 shapes to make,
where the first is the shape for the box packing
and the second is the rectangle shown above)
Zeitvertreiber (Pastime)





F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 2.5" x 4.5" x 1/2", 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has English text on the inside of the covers shown above,
and 32 pages with 96 shapes to make,
where the first is the rectangle for the box packing
Zeppelin





F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 2.75" x 3.7" x 1/2", 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has English text on the inside of the covers shown above,
and 32 pages with 98 shapes to make,
where the first is the rectangle for the box packing
and the second is the parallelogram shown above)
Kiebitz-Ei (Lapwing Bird's Egg)



F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 3+7/16" x 3+5/8" x 1/2", 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has 19 pages of text in multiple languages,
and 32 pages with 96 shapes to make,
where the first is the box packing shown above;
a scan of the booklet is shown on the following pages)
Teufeldien (Little Devil)





F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 2.75" x 3.7" x 1/2", 9 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has English text on the inside of the covers shown above,
and 32 pages with 96 shapes to make,
where the first is the rectangle for the box packing
and the second is the octagon shown above)
Heureka (Eureka)





F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 3.1" x 3.75" x 1/2", 8 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1917;
similar in construction to the Anchor Puzzle Tangram;
the inside of the cover shows how to pack the pieces into the box;
the booklet has English text on the inside of the covers shown above,
and 32 pages with 96 shapes to make,
where the first is the rectangle for the box packing
and the second is the shape shown above;
label across front is from F. A. O. Swartz, N.Y.)
The manufacture for the Richter Anchor Puzzles began in the 1890's, where the puzzles numbered above 17 were made in the World War I era. The 1893 Hoffmann book describes the Anchor, Circular, Cross, Pythagoras, and Tormentor puzzles (and also the Star Puzzle). A history of the Richter puzzles is presented in The Anchor Puzzle Book by Jerry Slocum (see also the Slocum and Botermans books). The puzzle boxes were made with a variety of cover art (see the following page), although the stone pieces, made with the Richter Co. patented process, are the same. Perhaps what made these puzzles so popular were the fun booklets that came with them, giving a host of shapes to make.
Here is a booklet that came with the Anchor Puzzle, and also a corresponding solution booklet that one could purchase by mail:


Generally, booklets have more or less the same cover art as the box top, but not always. For example, on the left and middle are booklets for versions of the Tormentor and Cross Puzzle that look very different from the corresponding box top, and on the right is a booklet for a version of the Anchor Puzzle that has blank covers (and nothing inside besides the problem figures):



Here are two examples of additional work booklets that came with the Anchor and Lightning Conductor puzzles:


Some box themes were highly regular; here are some examples (the last one in the first row is used on boxes numbered above 17, and the others for 17 and below, where the last three in the second row are dated in the The Anchor Puzzle Book as relatively late versions first made in 1922, 1925, and 1932 respectively):








Other themes used fun graphics (e.g., people thinking, specialized graphics, cartoons); here are some examples (all used on puzzles numbered 17 and below):















Richter 1
The Nine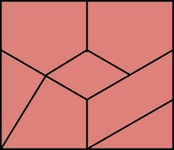
Richter 2
Lightning Conductor
Richter 3
Egg Of Columbus
Richter 4
Patience Prover
Richter 5
Trouble Killer
Richter 6
Heart Puzzle
Richter 7
Kobold
Richter 8
Anchor Puzzle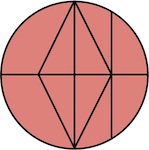
Richter 9
Circular Puzzle
Richter 10
"Cross Puzzle"
Richter 11
Not Too Hasty
Richter 12
Pythagoras
Richter 13
Tormentor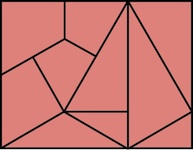
Richter 14
Be Quiet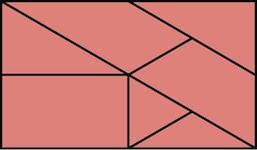
Richter 15
Sphinx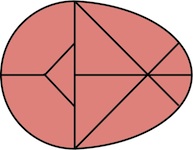
Richter 16
Magic Egg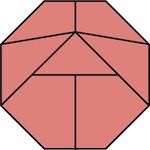
Richter 17
Wrath Breaker
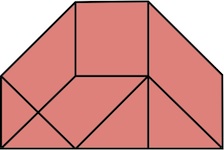
Richter 18
Archimedes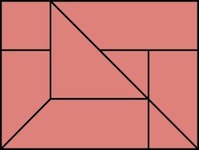
Richter 19
Ende Gut, Alles Gut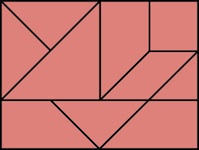
Richter 20
Pass Auf
Richter 21
Eile mit Weile
Richter 22
Sorenbrecher
Richter 23
Kopernikus
Richter 24
Pyramide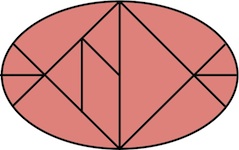
Richter 25
Nur Mut
Richter 26
Bose Siben
Richter 27
Ritze Ratze
Richter 28
Frisch Gewagt
Richter 29
Zeitvertreiber
Richter 30
Zeppelin
Richter 31
Kiebitz-Ei
Richter 32
Wer Wegt Gewinnt
Richter 33
Fur Kluge Leute
Richter 34
Hexenmeister
Richter 35
Teufeldien
Richter 36
Heureka
Here are pages from an old Richter Brochure (courtesy of Jerry Slocum, Puzzles Old And New, Copyright 1986, page 28); see also The Anchor Puzzle Book by Jerry Slocum.

Here (and on the following page) are the shapes used to make the 36 Richter Anchor Puzzles (courtesy of Jerry Slocum, Puzzles Old And New, Copyright 1986, page 28); see also The Anchor Puzzle Book by Jerry Slocum.
(second half of the figure from Puzzles Old And New, Copyright 1986, page 28)
The Anchor Puzzle Book, from: http://www.SlocumPuzzles.com
Richter Company U.S. Brochure, from: http://www.cs.brandeis.edu/~storer/JimPuzzles/ZPAGES/zzzRichterBrochure.html
Anker Page, from: http://www.ankerstein.org
Richter History, from: http://www.ankerstein.org/html/CO.HTM
Wikipedia Tangram Page, from: http://en.wikipedia.org/wiki/Tangram
Rubiks.com Double Tangram booklet, from: http://www.rubiks.com/World/Rubiks%20downloads.aspx
Rob's Tangram Page, from: http://home.comcast.net/~stegmann/tangram.htm
Slocum Database, from: http://webapp1.dlib.indiana.edu/images/search.htm?scope=lilly/slocum





a.k.a. Richter Picco Nr. T1
F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 2.125" x 2.125" x 3/8", 8 stone pieces, and problem sheet;
the Anchor Puzzle Book dates this puzzle as first made in 1913;
puzzle tray slides into the right side of the box with a small tab to pull it out;
top and bottom of box edge says "Richter Rudolstadt";
same pieces in a smaller size as Richter 13 Tormentor;
problem sheet has 26 shapes, where problem 11 shows how to pack into the box)
The first of three miniature Richter puzzles referred to as Picco or Piccolo (Nr. T2 is the same as Richter 12 Pythagoras; and Nr. T3 is the same as Richter 8 Anchor Puzzle; with the parallelogram piece divided into two triangles); see the Anchor Puzzle Book.
Further Reading
Indiana Slocum Archive (photos of Picco versions of Nr. T1 Nr. T2 a b c, Nr. T3 a b) from:http://webapp1.dlib.indiana.edu/images/search.htm?scope=lilly/slocum





a.k.a. Richter Hamleys
F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 2.125" x 2.125" x 3/8", 8 stone pieces, and problem sheet;
puzzle tray slides into the right side of the box with a small table to pull it out;
same pieces in a smaller size as Richter 13 Tormentor;
same size and pieces as Richter Piccolo Nr. T1, and like that puzzle,
problem sheet has the same 26 shapes, where problem 11 shows how to pack into the box)
Further Reading
Modern page of the London Hamleys toy store: from: http://www.hamleys.com/explore-stores.irs

"Schutzengraben-Geduldspeil"

"Zoologischer-Garten"
Richter Company, Germany, early 1900's.
(both puzzles cardboard box 3.1" x 3.1" x 1/2", 15 stone pieces, and problem sheet)
These two puzzles are the same except for the included direction sheet. The Anchor Puzzle Book describes the 1915 Trench Puzzle as made for World War I soldiers, and the 1916 Zoo Puzzle as a "neutral" puzzle made in Switzerland.





Richter Company, Germany, 1890's / early 1900's.
(cardboard box 3.75" x 3.75" x 1/2", 48 stone pieces, and booklet;
the Anchor Puzzle Book dates this puzzle as first made in 1892;
described on pages 87-90, 122-124 of the 1893 Hoffmann Book;
16 white right triangles, 8 white wedges, 8 black wedges, 16 black quadralaterals;
inside of the cover shows how to pack the pieces into the box;
inside of the box bottom has an add for "Dr. Richter's Pain-Expeller";
booklet has multi-language text inside covers and on pages A to Q at the front,
and 48 pages with 153 shapes to make)
Like Blumenspiel (using curved pieces) and Meteor One (using marbles), more of a two-dimensional building set than a puzzle.























--- 332 --- Star Puzzle, Continued


Different box and booklet cover art from the puzzle of the preceding page,
but otherwise the same)



Richter Company, Germany, circa 1915.
(cardboard box 8.8" x 8.8" x 5/8", 52 colored stone pieces, 6.75" x 6.75",
with 12 page blue problem and green solution booklets of 36 patterns)
More of a two-dimensional building set than a puzzle. Described on page 86 of the Anchor Puzzle Book, this is one of a number of Richter "Mosiac" puzzles made in the World War I time period that used colored tiles. The tiles are colored differently on each side; below is shown the arrangement shown above flipped over (in the horizontal direction), and two sample pages from the problem and solution booklets:



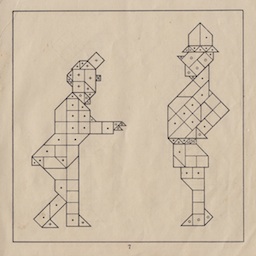

F. Ad. Richter & Co., Germany, early 1900's.
(cardboard box 6.3 by 6.3 by 5/7 inches, 4 colors marbles, and booklet;
more of a game than a puzzle, the object is to arrange the marbles into patterns;
in Richter's Puzzles and Pastimes catalog - see Anchor Puzzle references)



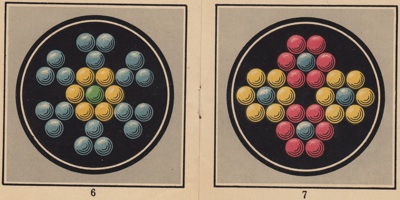



F. Ad. Richter & Co., Germany, early 1900's.
(wood box 8.75" x 8.75" x 2.5", 6 colors marbles, and booklet;
like Meteor 1, arrange the marbles into patterns;
also includes a Nine Mens Morris, board;
in Richter's Puzzles and Pastimes catalog - see Anchor Puzzle references)

a.k.a. Richter Anchor Puzzle
Wood puzzle purchased circa 2000; sleeve made by J. A Storer.
(wood tray and pieces with cardboard sleeve, 5+78" square by 3/8" thick)
The sleeve has the problems from the classic Richter Anchor puzzle:


"Wm. F. Drueke & Sons, Grand Rapids, Mich.", circa 1940?
(cardboard box 2.5 by 5.75 by 13/16 inch thick, and 7 wood pieces;
assembles to a 4.1 inch square by 5/16 inches thick)

Tryne Games Mfg. Inc., Lindenhurst, NY, copyright 1961.
(cardboard box 5.6 by 9 by 7/8 inch thick, booklet, and 7 plastic pieces;
assembles to a 5.4 inch square by 3/16 inches thick;
the problems in the booklet are similar to the Richter 8 Anchor Puzzle booklet; this puzzle should not be confused with Richter 12 Pythagoras)
(Same pieces as Richter No. 10 Cross Puzzle)

Kogner Bros. Inc., Tryne Game Division, East Paterson, N.J., circa 1960's.
(cardboard box 5.6" x 9" x 13/16" with plastic tray, booklet, and 7 plastic pieces;
assembles to a 5.4 inch square by 3/16 inches thick;
the problems in the booklet are similar to the Richter 10 Cross Puzzle booklet;
the box and booklet are not dated,
but the booklet references a copyright 1961 version of the Tangram that it calls "Pythagoras")
(Same pieces as Richter No. 10 Cross Puzzle)

Hi Ho Puzzle, 1932.
(2.75 by 2.5 by 5/8 inch cardboard box, 7 plastic pieces, and directions)
The pieces are made from Bakelite (an old type of plastic developed in the early 1900's). Below are the top and bottom edges of the box and one of the sides (the other side is the same). The directions show a sitting dog and suggest that many other patterns can be made.




Further Reading
Wilipedia Bakelite Page, from: http://en.wikipedia.org/wiki/Bakelite
(Same pieces as Richter No. 10 Cross Puzzle)


Sherlock Holmes Puzzle, circa 1960.
(2.9" x 3.6" x 7/16" plastic box, 7 plastic pieces, and directions;
the next page shows another copy still glued to the original 8.2" x 6.25" card)
(Same pieces as Richter No. 3 and Richter No. 16)




Scrambled Egg, Copyright ThinkFun 2002.
(9 metal pieces in plastic tray, 4 by 3.5 by 5/16 inches;
puzzle comes with clear plastic sleeve for storage;
booklet slides into tray bottom, and presents problems with solutions shown above)





Carrom Co., Ludington, Michigan, circa 1920s?
(cardboard box and 7 wood pieces, 3.6 inches square by 9/16 inches thick)
Like the Anchor Puzzle Tangram, the directions that were sold with this puzzle give a host of patterns to make from seven pieces similar to those of the Tangram.





ELZZUP Puzzle Co., Keene, N.H., circa 1900.
(3.3" x 3.3" x 3/4" wood box and 10 wood pieces)
This puzzle was sold in 2011 by a person who said it had been owned by Eleanor Dows of Laurel Mass., the sister of his grandfather, who was born in 1890. The back of the box top has her name in pencil, and her name and the town of Laurel Mass. is burned into the box bottom. The arrangment of the pieces into a square is not unique. In the spirit of the Anchor Puzzle Tangram, the goal is to make fun patterns with the pieces.







Wm. F. Drueke & Sons, Grand Rapids, MI, circa 1940's - 1960's.
(top: cardboard box 3.2"x3.2"x1/2", problem booklet, and 10 wood pieces;
middle: plastic box 8"x8"x1.2", problem & solution booklets, 10 wood pieces;
bottom: cardboard box 7.5"x7.5"x3/4", problem & solution booklets, 10 wood pieces)
In the same theme as the Anchor Puzzle Tangram, all three of these versions present 57 pages of 200 shapes to make. The first version above has only a problem booklet, which also includes English, French, and Spanish pages at the beginning that indicate that the puzzle may be purchased by mail for 50 cents, and that a solution booklet can be ordered for 25 cents; the back of this booklet shows how to pack the pieces into the box.
(from the 8x8" version)





























(from the 8x8" version)

































PIC-TUR-ETT Company, Mattapan, Massachusetts;
"PATENT APPLIED FOR"; all figures on directions and cards are copyright 1933.
(cardboard box, direction sheet, 15 problem ad solution cards, 4.25" x 4.25" x 1"))


Rockford Pattern Works, circa 1930's?
(4.25" square by 5/8" thick box, 9 wood pieces, and 4" square booklet;
some versions have the Rinehimer Millwork label on the box top)
Like the Anchor Puzzle Tangram, a booklet shows shapes to make. Here are the booklet pages (page 1 and the last page are shown together):












Further Reading
King Tut Wikipedia Page, from: http://en.wikipedia.org/wiki/King_tut
Rockford Foundries History, from: www.rockfordfoundries.com/about.cfm



German text on the package promotes Vision 2000; purchased 2010.
(cardboard box and four 7/16" thick wood pieces, 9.25" x 1.8" by 9/16")
In the theme of the Anchor Puzzle Tangram, using the same four pieces as the Missing T puzzle, the booklet gives 100 shapes to make, the first how to pack into the box and the last is the T:
















Further Reading
Vision 2000 Page, from: http://www.vision2020.org/main.cfm


Copyright ThinkFun 2008.
(plastic, 5" x 5" x 1.4")
In the theme of the Anchor Puzzle Tangram, 14 pieces can be arranged into many shapes. The box has a tray that slides out with 60 problem cards of shapes to make (that give hints and solutions on the back).
Further Reading
Problem card backs.

a.k.a. F Puzzle
Old design, 3D print files made by Fernando Jerez, 2016.
(Printed on a Monoprice Mini V1 3D printer at scale 160%,
from Thingiverse thing 2975065, 2019,
PLA plastic, 4 pieces and tray 2+1/4" x 3+3/4" x 3/16" inches)
An easy puzzle to pack the four F's into the tray:

Further Reading
Four F's Puzzle Thingiverse Page, from: http://www.thingiverse.com/thing:1666559

Magic Square, circa 1960?
(plastic box 2.5 by 1.75 by 1/2 inches and 4 plastic pieces;
assembles to a 2.5 inch square)

a.k.a. Square Me, Five Block Puzzle, Madagascar Madness
ThinkFun Binary Arts, 2003.
(plastic, 4-piece square is 3 inches, solved 5-piece square is 3.2 inches square)
People often quickly find the four piece solution and then get stuck trying "stretch" the puzzle just a little bit in a way that will accommodate an additional small square piece. If the four piece solution is 4 units square, it has area 16, the extra square has area 2, and the five piece solution has area 18 (forming a square that is just under 4.25 units square); for each of the pieces in the four piece solution, its orientation is 45 degrees counter-clockwise in the five piece solution:
Characterized on page 102 of the 1942 Filipiak book Filipiak book as "recorded in the records of antiquity", has been periodically made as a promotional item.

CSPI promotional circa 1975.
(plastic, solved 5-piece 2.9 inches square;
this was a company that J. A. Storer's father was a part of in the 1970's;
came with a wire loop which J. A. Storer replaced in 2007 with Snowbird key ring)


"Madagascar Madness", Behavioral Sciences Inc., 1969.
(5 inches square by 3/4 inch thick plastic box and five plastic pieces;
the square piece was lost and replaced with a green plexi-glass piece)
This puzzle is packaged with a tray for the 4-piece solution and the 5th piece loose; perhaps to guide the solvers thinking away from the 5-piece solution. The directions on a 4.5 inch square card inserted into the back give an interesting discussion of the geometry:

Further reading
Dickinson's Witch Hazel promotional, unknown age.
(3" x 4.5" envelope with cardboard pieces, solved 5-piece square is 4" square;
Dickinson's Witch Hazel was first made in 1866 and was still being made in 2000)

Five Block Puzzle, S.S. Adams Co. circa 1950?
(1/4 inch thick wood pieces, solved 5-piece square is 5 inches square)
http://www.lib.uconn.edu/online/research/speclib/ASC/findaids/
EEDickinson/MSS19960001.html

Designed by Wladimir Krasnouchow, distributed by Puzzle Master 2019; cardboard sleeve added by J. A. Storer.
(plastic, 4+3/16 x 3+11/16 x 1/4, the circle is .57 inches diameter)
In a theme like the classic Double Square puzzle, this clever puzzle presents the seemingly impossible task to pack the red circle inside the frame together with the five pieces. That is, somehow you have to get the red circle to fit into this already crowded tray:

One having seen the solution, is unlikely to forget it. If you are frustrated, here is a hint (shown upside down so it won't read it by mistake):



a.k.a. T Puzzle, Magic T, Cut-Up T, Pa's T Puzzle,
Great American T Puzzle, White Rose Ceylon Perfect T Puzzle, Lash Bitters T Puzzle.
Old design, copyright 1898 Lash Inc., this copyright ThinkFun Binary Arts 2003.
(plastic, 4 pieces, 3.1" high by 3" wide when solved)
The four pieces can be positioned to form a T as shown above. The HIQU puzzle has a booklet of problems based on these pieces. This is an old puzzle that has been produced many times; here is a nice antique wood one:

Pa's T Puzzle, circa 1940's.
(cardboard box 4.6 by 1.75 by 11/16 inches and 4 walnut pieces,
5" high by 4.75" wide when solved;
box edge says "PA'S T PUZZLE No. P 20 WM. F. DRUEKE & SONS Grand Rapide, Mich.")

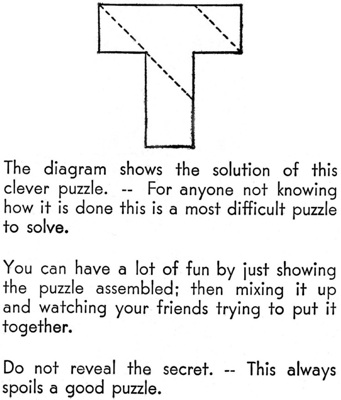
S. S. Adams Co., circa 1950's.
(3.5" cardboard sleeve with cardboard directions and dark green plastic pieces)

Magic T Puzzle, unknown manufacture.
(plastic box 2.5 by 1.75 by 1/2 inches and 4 plastic pieces)
Marx Toys, circa 1960's.



(5.5 by 7 inch cardboard card with plastic pieces;
solution sheet in plastic bag and big question mark with company logo behind the bag)
Further Reading
T Puzzle Wikipedia Page, from: http://en.wikipedia.org/wiki/T_puzzle



"Shackman N.Y.1 No. 3627 Cross Puzzle", made in Japan, circa 1960's?
(cardboard box 5+1/8" x 1.75" x 5/8", direction sheet, and six 1/8" thick wood pieces
consisting of four identical Z shapes and two identical L shapes;
assembled cross is 4+3/8" high by 3 inches wide at the cross, and 1" wide at the tips.)


Hikimi Nob Yoshigahara Puzzle Collection, Japan, Copyright 1987.
(box and 6 wood pieces, 3.7" x 6.1" x 3/4";
included are directions in Japanese that give the problems shown above)

Designed by T. Linden, made by E. Fuller, 2009.
(velour bag and 7 English Brown Oak pieces, 3 inches assembled)
There are two 1x1x3 unit pieces each with one 45 degree pointed tip, three 1x1x2 unit pieces each with one 45 degree pointed tip, and two unit triangles.
By cheating just a little bit, an upper case H can also be formed. On the left below the upper right tip of the H is missing a unit triangle. In the middle, the pieces have all been rotated 90 degrees and are arranged so that the H looks perfect from above (it is formed from two 3 unit pieces on the left, two triangles for the cross, and three 2 unit pieces on the right, where there is a missing triangle on the top right tip when viewed from the side). On right below, again the pieces have all been rotated 90 degrees and are arranged so that the H looks perfect from above (it is formed from a 2 and 3 unit piece on each side, a 2 unit piece and a triangle for the cross, and the remaining triangle filling in one of the tips, with the other three tips having a missing unit triangle when viewed from the side).


Promotional puzzle from Mr. Puzzle Australia, 2008.
(6 thin flexible plastic pieces)



Made by interlocking Puzzles 2000.
(directions card and 6 identical Zebrawood pieces, each 2.25 inches)
Here is what Interlocking Puzzles said:"There are at least eighteen different challenges requiring the special angles and three, four, five, or six pieces of our Make a Square puzzle. Geometric shapes possible include triangles, squares, rectangles, pentagons, hexagons, parallelograms, and trapezoids. This tiling puzzle seems simple, but it is quite challenging to find all the solutions. These 6 pieces are each over 2 inches long, which allows the largest finished shape to be over 7 inches across the diagonal."

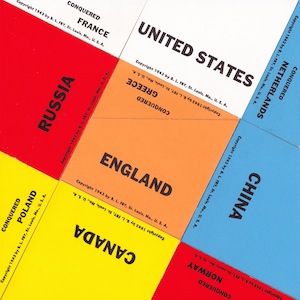
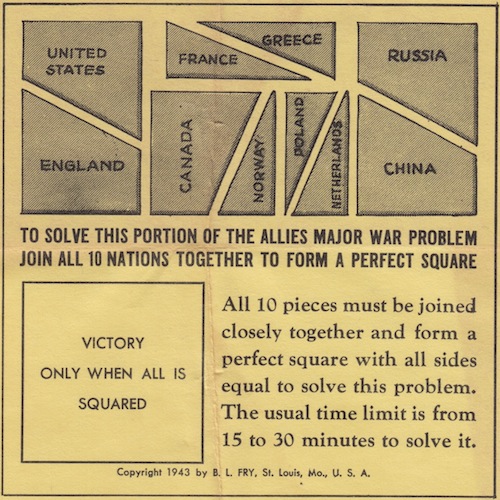
Copyright B. L. Frye, St. Louis, MO, 1943.
(5 identical shaped large cardboard pieces and 5 identical shaped smaller cardboard pieces,
in a cardboard envelope 3+5/8" x 3+7/8", with directions on the inside)



Designed and mad by Stewart Coffin, 2013
(maple and paduk on a plywood bottom, 3.7 x 3.7 x 3/4", signed on the bottom;
one of 4 puzzles purchased during a visit with the designer in 2014)
Shown on page 155 of the Coffin AP-ART book. This puzzle is already a challenge due to the number of pieces and that they are two sided. Also, when it is given to someone with the pieces out of the box, there is a natural tendency to put them in so that they fit tight into the corners, in which case one inevitably ends up with having two pieces left that will not fit into the final corner. It is only after noticing that although the pieces are precisely cut, space is left between the packing and sides of the frame, and so something seems wrong (in fact, that space is equal to the space in the corners when the puzzle is correctly solved).


Designed by Stewart Coffin, made by Eric Fuller 2013.
(Ebony, Canarywood, Sapele, acrylic plastic top, 3.75" x 3.75" x 7/8";
6 puzzle pieces with the shapes shown above)
The plastic top has some rectilinear openings through which the pieces can be inserted and manipulated. Remove the pieces, mix them up, and then re-insert them. The underside has a rim that allows one to play with piece assembly without the plastic on top. Here is what the puzzle maker says:"I've constructed this with a solid Sapele body, shouldered on the corners for strength. The acrylic top is precision cut on the laser and the bottom is a solid floating canarywood panel chosen for contrast against the dark ebony. The fit is precise, with rounded corners to enable the very tricky rotational solution."The puzzle maker also quotes from the designer:"The three puzzles in this category all have a 5x5 square two-sided tray. On the back side is a simple framed square for practice exercises. The front side has a Plexiglas cover with openings cut in it through which the puzzle pieces are inserted. Of these three, The Decoy (#187-A) is by far the most difficult and my favorite. It is the only one that requires a slightly loose tray or rounding of corners to solve."
Plas-Trix Co., Jamica, NY, circa late 1950's



(plastic box and 12 plastic pieces, 4.75 by 4 by 5/16 inches)
Made by the same company and packaged like the Krazee Checkerboard Puzzle and the Krazee Links, but easier. Here are the packing instructions on the back of the directions and a solution:


Purchased 2004.
(wood base with metal pins, 7 wood pieces, 5 inches)
A board with metal pins must have 7 wood pieces (with holes) placed on it to form a square. The solution is not unique.



Copyright ThinkFun 2008.
(plastic, 3 inches)
Pack the four T's into the square. On the left above is the top side of the puzzle solved, and on the right above is the easier underside of the puzzle (with a larger square) solved.

Designed by E. Nagata, copyright Binary Arts 2002.
(plastic and metal, 3.5 by 4.5 by 3/8 inches thick)
The puzzle comes with the pencils placed on one side of the board as shown above. The challenge is to flip the board over and pack them into the other side:


Designed by Bill Cutler, made by Walt Hoppe, and purchased 2006.
(15 pieces including the pearl and shell, 4.5 inches)
The goal is to place the thirteen wedge shaped pieces and the pearl (the little round piece) into the shell. After achieving the configuration shown above, the pearl is off to the right in the keeper hole, the pieces meet at a point in the center, and there appears to be no extra space. Now for the fun; the pieces can all be flipped over and space made to place the pearl in the center of the shell:


Designed by Bill Cutler and made by Walt and Chris Hoppe, 2008.
(25 wood pieces, each 3/16 inch thick, solved puzzle is 6.5 inch diameter circle)
Pack the 25 pieces to form a circle; here is what the directions say:"These pieces can be used to tile the plane non-periodically. They are a variation of the Penrose "Kites and Darts" tiles. Each barn is equivalent to the Penrose "Dart" piece, and the silos and tractors are each one-half of a "Kite" piece."The graphics on the 25 pieces are:(5) barn with a siloFurther Reading
(5) barn with a double silo
(5) barn (no silo) with a tractor
(5) barn (no silo) with a tractor towing a cart
(3) barn with a double silo and tractor
(2) barn with a silo and tractor towing a cart
Note: The directions say that some puzzles were made with the quanties 3 and 2 reversed.
Wikipedia Penrose Tiling Page, from: http://en.wikipedia.org/wiki/Penrose_tiling

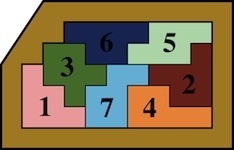
Designed by Minoru Abe, purchased 2014.
(cardboard box, wood tray, and seven wood pieces)
Find all 7 ways to pack the 7 pieces, each consisting of 6 unit squares, into the tray that is 5 units high by 9 units wide with 3 units blocked out in the upper left corner; one is shown above, and here are the six others:

a.k.a. Polyominoes
Old puzzle, this one made by Yasumi, 1995.
(wood, box and 12 pieces based on 0.75" inch cubes)
The 12 distinct shapes formed from 5 connected squares are the pentominoes (called polyominoes by Solomon W. Golomb, Charles Scribner's Sons, NY, 1965):
Total area is 60, and sizes 6 x 10, 5 x 12, 4 x 15, and 3 x 20 can be formed. There are known to be 2,339 distinct ways to form a 6 x 10 rectangle, excluding rotations and reflections. In contrast, there are 1,010 solutions for 5x12, 368 solutions for 4x15, and 3 x 20 has a unique solution except for rotating a central portion by 180 degrees.
A piece is landlocked if it does not touch one of the borders of the rectangle. Eric Harshbarger has determined that there are no 6x10 rectangle solutions with 5 or more landlocked pieces, but there can be solutions with 0, 1, 2, 3, or 4 landlocked pieces (e.g., there are 207 solutions of the 6x10 rectangle with four landlocked pieces, 1,111 with three, 864 with 2, 155 with one, and only a couple with zero).
R. M. Robinson of the University of California at Berkeley proposed the "triplication problem": Given a pentomino, use 9 of the other pentominoes to construct a scale model, 3 times as wide and 3 times as high as the given piece (all 12 are possible).
Pentominoes are traditionally flat pieces that can be arranged to form 2-dimensional patterns. However, if the pieces are made to be 1-unit thick, then fun 3-dimensional patterns can also be made, including a 3 x 4 x 5 solid, and stairs that are 6 wide by 4 deep by 4 high.
(The shaded area of the 3x20 solution may be rotated by 180 degrees.)

From the directions sold with the Yasumi version:
From the directions sold with the Interlocking Puzzles version:


Made By B. Cutler, 1989.
(3.25"x4"x2.375" plastic box and 12 two-color wood pieces with 3/4" cubes)
Can be used like any other pentominoes set. In addition, it is made from light and dark woods so that it can be solved in a 3x4x5 box where colors have a checkerboard pattern on all sides. Here is the diagram of the pieces from the directions that came with the puzzle:
Sold with this puzzle was printout of a number of solutions. Here is the one suggested; the pieces have the names 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, and this figure shows the three planes of the checkerbox:ABB5C A666C A636C
BB555 A7778 3333C
B9958 A9778 9944C
11111 22228 44428
From the directions sold with the Yasumi version:
Shown on Nivasch's Page:
Further Reading
Harshbarger's Page, from: http://www.ericharshbarger.org/pentominoes
Mathworld Page, from: http://mathworld.wolfram.com/Pentomino.html
CIMT Page, from: http://www.cimt.plymouth.ac.uk/resources/puzzles/pentoes/pentoint.htm
Gerard's Page, from: http://www.xs4all.nl/~gp/pentomino.html
Huttlin's Page, from: http://members.aol.com/huttlin/pentominoes.html
Nivasch's Page, from: http://yucs.org/~gnivasch/pentomino
Mark's Page, from: http://mathsevangelist.wordpress.com/2012/08/24/packing-pentominoes
Jankok's Page, from: http://homepages.cwi.nl/~jankok/etc/Polyomino.html
info Page, from: http://www.theory.csc.uvic.ca/~cos/inf/misc/PentInfo.html
Gottfriedville Page, from: http://www.gottfriedville.net/puzzles/colorgame/solutions.htm
Belgium Pentominoe page, from: http://home.scarlet.be/~demeod/indexe.html
Puzzle Will Be Played page, from: http://www.asahi-net.or.jp/~rh5k-isn/Puzzle
Fletcher's Page, from: http://www.andrews.edu/~calkins/math/pentos.htm
Wikipedia Page, from: http://en.wikipedia.org/wiki/Pentomino
Negahban Design Patent, from: www.uspto.gov - patent no. 385,311
Further reading about some related puzzles:
Lester Patent, from: www.uspto.gov - patent no. 1,290,761
Wadsworth Patent, from: www.uspto.gov - patent no. 3,964,749
Sarkar Patent, from: www.uspto.gov - patent no. 5,544,882

Designed by P. F. Ramos 2004, made by Interlocking Puzzles.
(wood frame and 12 pieces, 3.75" x 3.75" x 3" inches)
Standard pentominoes are the 12 different planar shapes that can be formed from 5 squares. There are 17 non-planar pentomino shapes (each made from 5 cubes). Here, 12 of them (which can be can be grouped into 6 mirror image pairs) must be packed into a 4x5x5 box frame; 40 units are used by the frame, leaving exactly 60 units of space to pack these pieces:
According to the sheet that came with the puzzle there are 54,189 possible ways these pieces can fit (in the sense that you could build the box around them), of which 23,549 of them can be achieved by starting with the box frame and inserting and moving pieces. Here is the layer by layer representation of the solution that came with the puzzle (X is the box):
A
B
C
D
E
F
G
H
I
J
K
LIn the orientations shown in the figures above, pieces can be inserted as follows:
top layer:
XXXXX
XJAFX
XJJFX
XCCFX
XXXXX2nd layer:
XGAIX
GGAFF
GJAAK
HJCDK
XDDDX3rd layer:
XGBIX
BBBII
EEELL
HHCKK
XDCKXbottom layer:
XXXXX
XBEIX
XHELX
XHLLX
XXXXX
1. B from behind.
2. I from behind.
3. G from behind.
4. E from below.5. H from below.
6. A from behind.
7. L from the right.
8. K from the front.9. F from behind.
10. C from above.
11. J from the top.
12. D from the front.







a.k.a. Sneaky Squares, Stark Raving Cubes, Block Out, Square Fit, KUBI
Designed by Bill Cutler, wood version made by J. Devost, 1983.
(left: oak, 4.5 inches square by 2.25 inches high;
middle: Sneaky Squares / Start Raving Cubes, plastic, 4.5" square by 2" high;
right: Block Out / Square Fit, 3" square by 1.25" high)
Four pieces cut at odd angles (so that they not quite cubes) must be placed into the box (a three piece version has also been made). Inserting one at a time will not work. To solve, arrange them on the table so that the top is level and square, push them together at the bottoms, and drop them into the box. Here is what the pieces look like in their solved positions, outside the box:


a.k.a. The Third Degree
Designed by Bill Cutler, made by W. Hoppe, 1995.
(wood, 3.75 inches by 1.75 inches high)
Three pieces that are cut at odd angles (so that they not quite the same) must be placed into the box. Like the larger Block Head puzzle, putting them in one at a time will not work; to solve, first arrange them on the table so that the top surface is level and a hexagon, and then push them together at the bottoms and drop them into the box. Here is what the pieces look like in their solved positions, outside the box:


Designed and made by Stewart Coffin, 2014.
(maple pieces and sides on plywood base, signed on the bottom;
2.25" high, top edges of walls are 2", balls are 3/4" diameter;
one of 4 puzzles purchased during a visit with the designer in 2014)
Unpacking requires moving the top two pieces out of the way and removing the bottom one first:





Elverson Puzzle, 2002.
(wood box and 13 wood rods, 2.75 by 7.5 by 1.75 inches)
Pack 13 wood rods into the box. Here are th directions on the bottom of the box:

Here is the solved top layer taken out, showing the solved bottom layer in the box:


Made in the U.K., circa 2000?
(wood box and 18 wood rods, 2.7" square, with recessed silver dot stickers)
Pack the 18 rods into the box. A solution of 6 layers going from top to bottom is shown here from upper left to lower right (note that the rods of the top layer shown in the upper left all need to be rotated 180 degrees, as does the first rod in the second layer):



Copyright Pacific Game Company Inc., Japan, 1970.
(plastic, 3.25" square)
The object is to pull out all the pegs, mix them up, and reassemble. The instruction booklet shown on the following pages says there are 12 ways to do it, shows how to do two of them, and gives blank diagrams to color in the other ten solutions. Here is the solved cube shown above flipped over to show the other three sides:


Designed by John Conway, copyright ThinkFun Binary Arts 2003.
(plastic, box and 9 pieces, 1.75" solved)
Also known as Conway's Curious Cube, and described on pages 736-737 of the Winning Ways books. Three unit cubes and six 1x2x2 pieces must be placed in a 3x3x3 box. In the unique solution, the three unit cubes line up diagionally through the cube from a corner to the center to the opposite corner:


Here is the solution that was sold with the puzzle:



"BRADLEY'S, CUBE ROOT BLOCKS, No. 2, TO TWO PLACES", circa 1940?
(wood box and 15 pieces, 3.25" square;
pieces based on 1/2 unit cubes;
two unit size cubes, one 3x3x3 cube, and three each of 1x1x3, 1x1x4, 1x3x3, 1x4x4)

Designer unknown, made by and computer analysis done by Bill Cutler 1979.
(wood box and 18 wood pieces, 4.8" by 6.8" by 1.7" thick)
A box of inside dimensions 18 x 28 x 6 units into which must be placed 18 two unit thick pieces of sizes 4x9, (2) 5x9, 5x18, 5x21, 6x7, 6x10, 6x13, (2) 7x8, (2) 7x13, 7x18, 8x18, 9x11, 9x13, 10x11, and 11x11. Cutler's analysis showed four solutions (not counting rotations and reflections), all placing the 4x9, 6x7, and 6x13 pieces on end. Here is one of them, from the sheets that came with the puzzle (copyright by and courtesy of Bill Cutler).
top layer middle layer bottom layer
Exchanging the middle and bottom layers gives a second solution, and these two solutions each have an alternate version by exchanging the 7x18, 5x21, 6x10 pieces on the top layer with the 7x13, 5x18, 10x11 pieces on the middle layer.


Designed by Bill Cutler with a computer 1992, made by Tom Lensch 2004.
(Wenge box with Bubinga pieces, 5 inches)
Here are the layers of the unique solution, from the sheet that was sold with the puzzle (copyright by and courtesy of Bill Cutler):

A host of puzzles have been made that require the solver to match adjacent edges or faces based on colors or patterns. Perhaps the most famous example of this type of puzzle is Instant Insanity, where one must line up four colored cubes so that each side has all four colors.

a.k.a. Rubik's Mini Tangle
Circa 1990, this one by J. A. Storer 2007 from a Rubik's Tangle 5x5.
(nine 2" cardboard squares in a 2.75 by 4 by 3/4 inch plastic box)
Arrange 9 squares in a 3x3 array so that edges match. Each square has the same pattern of 4 tangled ropes that has two connections on each edge. Different squares have a different combination of the four colors (red, green, blue, and yellow).
Jaap's Page indicates that this puzzle may have been produced as a give-away to promote the Rubik's Tangle 5x5 puzzle. The puzzle pictured here was made by using squares from a Rubik's Tangle 5x5. It's solution is the upper left 3x3 portion of the first solution to Version 1:
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles
Thurston Patent, from: www.uspto.gov - patent no. 487,798
Rankin Patent, from: www.uspto.gov - patent no. 606,338

Produced in 1995.
(nine 2" square plastic pieces, patterns on both sides)
Arrange 9 squares in a 3x3 array so that edges match. Each square has on both sides the same pattern of 4 tangled ropes that has two connections on each edge. Different sides of different squares have a different combination of the four colors (red, green, blue, and yellow). More confusing than Rubik's Tangle 3x3 because one has to decide how to flip the pieces.
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/tangle.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/r90/tangle.htm
Thurston Patent, from: www.uspto.gov - patent no. 487,798




Rubik's Tangle 1, 2, 3, and 4, Matchbox 1990.
(Box and twenty seven 2 inch cardboard squares.)
Arrange 25 squares in a 5x5 array so that edges match. Each square has the same pattern of 4 tangled ropes that has two connections on each edge. There is one square for each of the 24 possible combinations of the 4 colors (red, green, blue, and yellow), and one duplicate square. The only difference between Rubik's Tangle 5x5 Versions 1, 2, 3, and 4 is which piece is duplicated. By taking three pieces from a spare set, a single set of 28 squares can be made where three of the duplicates are left out to make one of the 4 puzzles. Below is a set made by starting with a Version 3 and adding three squares taken from a Version 2; the four duplicate squares have been labeled with a number on the back.



Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/tangle.htm
Thurston Patent, from: www.uspto.gov - patent no. 487,798
Rankin Patent, from: www.uspto.gov - patent no. 606,338


"Made in West Germany" by Haba.
(3.75" x 3.75" x 1.8" cardboard box with nine wood pieces, each 1.75" x 1.75" x 7/16")
If the solution shown is rotated 135 degrees clockwise then it corresponds to the figure on the cover by mapping the four characters to the colors of the puzzle (in fact, by looking carefully, one can see a resemblance between the characters and the actual colored figures of the puzzle).



Price, Stern, Sloan Inc., Los Angeles, CA; Pig and Frog 1989, Train 1991.
(3.25 by 5.4 by 5/8 inch cardboard box and nine 3 inch cardboard pieces)
Like Rubik's Tangle 3x3, the directions on the back ask you to arrange the nine squares in a 3 by 3 array so that adjacent edges match; the Crazy Train directions state that there are exactly two solutions and are written in both English and Spanish.




Copyright 1997 McDonalds, GamesCo.
(cardboard box containing nine 5" square cardboard pieces)



McDonald Land Guzzle - "Birdie"



McDonald Land Guzzle - "Grimace"



McDonald Land Guzzle - "Bus"




a.k.a. Infants' Hospital - The Magic Line
Chad Valley Co. Ltd., Harborne, England, 1920;
made for the Infants Hospital in Vincent Square, London, founded by R. Mond.
(cardboard box and 16 cardboard pieces, 7" x 6.25" x 1/2";
instructions on the underside of the box top;
based on a 6x6 grid with four 1x3 pieces, and 12 1x2 pieces;
see also Infants' Hospital Puzzle, Dad's Puzzler - Exchange Version / Infants Hospital, A Ward In The Infants' Hospital, Infants' Hospital Jigsaw Puzzle)
The goal is to make the line go continuously from the start position at the bottom and end at the special "HEALTH" piece. Don't view at the solution before you try it; it's harder than it looks.




a.k.a. Endless Chain
Plas-Trix Co., Jamica, NY, circa 1957.
(plastic box and 14 plastic pieces, 4.75 by 4 by 5/16 inches;
same size / shape box as the Krazee Checkerboard Puzzle that is shown
on pages 57-58 of the Haubrich book, which gives the manufacture date; a puzzle like this is shown as the "Endless Chain" on page 99 of the 1893 Hoffmann book)

Milton Bradley 1984.
(cardboard box and 12 plastic pieces, 7 by 5 by 1.5 inches;
"Lost Rope" is a translation of "Faden Verloren" that is written on the box.)

Made by Milton Bradley, 1987.
(plastic, 5 inches)
Remove the hexagonal pieces from the pegs and then try to put them back so that the numbers on all edges match. Same puzzle as the Circus Seven puzzle,, (numbers 1 through 6 correspond to the colors red, green, blue, yellow, white, and orange). For a computer, the solution space is small: 7 choices for the center piece, 6 choices for the first outside piece, 5 choices for the second, etc., for at most 7! = 5,040 positions to try. Here are the directions that came with it:

Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/circus.htm

a.k.a. Mind Exerciser
Masudaya, Japan, circa 1980's?
(4.25" by 1.75" high plastic box and seven hexagonal plastic pieces)
Arrange the seven hexagons so that adjacent edges match. Like the Circus Puzzler, but a larger size puzzle with different color patterns. This is the same puzzle as Drive Ya Nuts, (the colors red, green, blue, yellow, white, and orange correspond to the numbers 1 through 6).

Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/circus.htm

a.k.a. Color Matcher
Circa 1980's?
(2.9" by 1.5" high plastic box and seven hexagonal plastic pieces)
Arrange the seven hexagons so that adjacent edges match. Like the Circus Seven puzzle, but a smaller size puzzle with different color patterns. Jaap's Page shows a number of other color variations for which this puzzle was made.
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/circus.htm

a.k.a. Spot Color
Made in China, purchased 2007.
(wood box and six wood circles with colored spots, 4 by 4 by 7/8 inches)
Arrange the six circles in a hexagon arrangement so that colored dots match; here is a closer view of the solution:

Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/circus.htm

Peter Pan Playthings, 1986.
(9.4 by 6.4 by 1 inch cardboard box, plastic base, and 6 plastic hexagons)
Jaap's Page gives two solutions, the one shown above and this one::

Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/circus.htm


Unknown manufacturer.
(7 cardboard hexagons, 2.25" point to point, in a 2.75" x 4" x 3/4" plastic box)

Purchased from Mefferts, 2007.
(plastic bag and 9 cardboard triangles, each 4 inches on a side)
This puzzle comes in a number of patterns, this is the "Dizzy Dolphins" version:


Lagoon Games, 2000.
(2 by 6 inch cardboard box with 37 hexagonal cardboard pieces)
Instructions on the box:Solution provided by the manufacturer (http://www.give-me-a-clue.com):


Lagoon Games 2007.
(plastic box and 18 half hexagon plastic plates, 3 by 5 by 3/4 inches)
Form a big hexagon from the 18 half hexagon pieces so that edges match. Puzzles of some type using half hexagons have been around for a long time (e.g., the 1924 patent of A. Chrehore). Here is the solution provided by the manufacturer (http://www.give-me-a-clue.com):
Further reading:
Crehore Patent, from: www.uspto.gov - patent no. 1,495,576


a.k.a. Other Name
Patented by xxx, purchased from xxx.
(cardboard box and 8 cardboard pieces, 5.2 by 5.2 by 7/8 inches)


Copyright Binary Arts 1993.
(cardboard box and 15 cardboard pieces, 5.2 by 5.2 by 7/8 inches)


Copyright Great American Puzzle Factory, 1996.
(cardboard box and 17 cardboard pieces, 5.5 by 5.5 by 1 inch)
Patented by C. R. Weinreb 2000, made by Albatross Games / Toysmith Group 2006.


Transposer 6.
(6 cardboard pieces, each 3.5" on a side;
front and backs shown above)

Transposer Bonbons.
(6 cardboard pieces, each 3.5" on a side;
front and backs shown above)
Each circle on the plate is either colored or empty, and the problem is to stack the plates so that the two sides are a specified solid colors (Bonbons also gives some easier problems for one side). Jaap's Page presents solutions for these and some similar ones. Here are the problems given in the directions, which list them in order of increasing difficulty:

Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/trixxy.htm
Weinreb U.S. Patent Application, from: www.uspto.gov - no. 2005/0225032


Same manufacture as Transposer 6 and Bonbons.
(4 cardboard pieces, each 3.5", backs shown below fronts in photos above)
Four plates must be stacked so that a path of a specified color on each side color connects the corner dots (and there are easier problems for only one side). Here are the ten problems that the directions list in increasing difficulty:
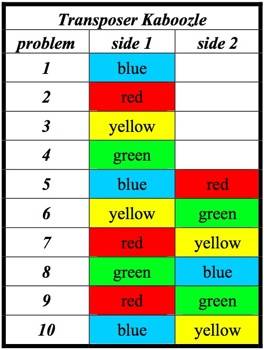


Tantrix Games 1997.
(holder and 10 plastic hexagonal pieces, 1.6 by 2.25 by 2.25 inches high)
Ten hexagonal tiles (numbered 1 through 10 on the backs) can be arranged in patterns, the highest level challenge being to make a loop of a given color (and matching edges of all adjacent tiles). The two sets shown above have different holders and background color, but the same tile patterns. Below, on the right are excerpts from the directions that came with the puzzles and on the left three ten tile loop solutions that are presented on Jaap's Page together with solutions to related puzzles (yellow and blue are switched from the sets shown here).
Further reading:




Jaap's Page, from: http://www.jaapsch.net/puzzles/tantrix.htm
Tantrix Home Page, from: http://www.tantrix.com

Tantrix Games 1991.
(mesh bag and 10 plastic hexagonal pieces, 1.8 inches point to point)
Like Tantrix Discovery, ten hexagonal tiles (numbered 1 through 10 on the backs) can be arranged in patterns, the highest level challenge being to make a loop of a given color (and matching edges of all adjacent tiles) or to make a pyramid with a continuous line through it. Four colors are used (as compared to three with Tantrix Discovery). Here are solutions presented on Jaap's Page for blue and red loops, a blue pyramid, and three red pyramids (the color white here is yellow there):






Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/tantrix.htm
Tantrix Home Page, from: http://www.tantrix.com

Patented by K. Minami and T. Nishimiya 1984, made by Tomy.
(plastic with colored metal ball bearings, 4.3 inches square by 1/2 inch thick)
Turning a wheel on the side causes the center ring to turn one direction and all the other rings to turn in the opposite direction. When solved, the center ring and three of the outer rings have silver ball bearings, and the other three outer rings have bearings colored red, green, and blue, and the center ring is missing one ball bearing. The one missing bearing allows bearings to be moved around by turning the rings and transferring a bearing from one ring to an adjacent one that currently has the empty position. After mixing it up, it is difficult to get it back to the solved position because rings cannot be rotated individually.
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/gears.htm
Minami and Nishimiya Patent, from: www.uspto.gov - patent no. 4,468,033

Copyright Eng's I.Q. Company Ltd. 1987.
(metal, 15 inches)
Each of 12 discs is colored with the same eight colors, but in different orders. The two discs on the left and right sides are attached to an arm (that rotates). In the center is a long arm, on its ends two shorter arms, and on their ends arms with pairs of discs. The discs themselves can all rotate. The task is to rotate the arms to place the discs in a straight line and then rotate the discs in such a way that colors match between adjacent discs and also between the left and right ends. The analysis on Jaap's Page shows that there are 12 ways to do this, but only one of them uses all eight colors:

Here is a side view of the arms when the discs are lined up in a straight line (as with a solved position):

Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/spectra.htm
Lamphere's Article, from: http://portal.acm.org/portal.cfm


a.k.a. Katzenjammer, (Great) Tantalizer, Face-4, Cube-4,
Bognar Balls, Taktikolor, Frantic, Diabolical, Damblocks,
Symington's Puzzle
Patented by F. Schossow 1900, this popular version by Parker Brothers 1967.
(standard: four plastic cubes, each 1.25 inches square;
mini: four plastic cubes, each 5/8 inches square)
Arrange the cubes in a line so that each side has four different colors (it is not possible to arrange them so that all colors on a side are the same). The puzzle, in both the standard and the mini version, was sold without a box, wrapped with the directions:


The solution is unique up to the ordering of cubes or rotating them all 180 degrees in one dimension (the mini is the same except that green and red are reversed);

Further Reading
Wikipedia Page, from: http://www.wikipedia.org/wiki/Instant_Insanity
1900 Schossow Patent, from: www.uspto.gov - patent no. 646,463
1932 Silkman Patent, from: www.uspto.gov - patent no. 2,024,541
1975 Estimating the Efficiency of Backtrack Programs, by Donald E. Knuth,Mathematics of Computation 29:129, 121-136, from: www.ams.org1981 Bognar UK Patent Application, GB 2,076,663.
2016 The Mutando of Insanity, by Érika. B. Roldán Roa, G4G12 Exchange Book Vol. 2, 135 - 144,from: www.gathering4gardner.org
Efficient algorithms are not known for finding Hamilton cycles (let alone two disjoint ones). However, this is a small graph, and it provides an organized way to search for these two cycles rather than playing with the cubes and trying to remember what has been tried.
- Draw four vertices), and label them green, white, blue, red; it doesn't matter how they are arranged (after solving, the figure below was re-drawn to look nicer).
- Number the cubes from 1 to 4 and for each of the three pairs of opposite faces on each cube, draw an edge between the two vertices of the corresponding colors and label that edge by that cube number (a total of 12 edges).
- Look for a Hamilton cycle (that passes through each vertex once) with a different label on each edge; this cycle is shown with the thick edges below (it is also ok to use set of smaller disjoint cycles but that doesn't help here).
- Find a second Hamilton cycle (or set of cycles) with a different label on each edge, that does not uses any of the edges in the first cycle; this cycle is shown with the hashed edges in the figure below.
- Traverse the thick edge cycle to set the top edges (green to blue set the top and bottom of cube 3, blue to white to set the top and bottom of cube 2, white to red to set the top and bottom of cube 4, and red to green to set the top and bottom of cube 1).
- Set the front/back edges with the hashed cycle by rotating each cube (without changing the top and bottom).

cycle 1: G - 3 - B - 2 - W - 4 - R - 1 - G
cycle 2: G - 2 - B - 1 - W - 3 - R - 4 - G


Parker Brothers, Copyright 1986, made in China.
(same size 1.25 inch plastic cubes as the 1967 puzzle)


Katzenjammer Puzzle, patented by Frederick A. Schossow 1900.
(cardboard tray & sleeve, and four 3/4 inch wood cubes)
Same as instant insanity with red -> hearts, green -> clubs, blue -> diamonds,
white -> spades, and cube 3 has the two hidden faces reversed:

These two puzzles have identical cubes (except the green color of the clubs on the right is faded). Here are the top, front, and back, of the two boxes, which are similar but not the same, and also the bottoms, where the one on the left is blank and the one on the right has promotional text:








FOURACE Puzzle, Britain, 1913.
(cardboard box 1+7/8" x 1+7/8" x 3+7/8", and four paper covered wood cubes,
where the cube edges vary in length from 13/16" to 15/16")
Box says "Provisionally Protected"; Stegman's Page credits J. Slocum as dating this puzzle to Gamage's in Britain 1913. The solution is the same as for the Katzenjammer Puzzle:

Here are the top, front, back, and bottom sides of the box (the box back advertises "The Great Card Puzzle"):





Great Tantalizer Puzzle, provisional patent no. 18945, not dated.
(cardboard box, and four 3/4 inch wood cubes)
Same as instant insanity with green -> white, white -> brown, and cube 3 has the two hidden faces reversed:

Here are views of the left end, top, front, bottom, back, and right end:


Tantalizer, made in England, not dated.
(cardboard box, solution sheet, and four 3/4 inch wood cubes; packaged with tie wraps to cardboard back shown on right above)
Same as instant insanity with yellow instead of white:

The solution sheet that came with the puzzle shows the same solution as above,
with cubes in the order 1, 4, 2, 3 and all rotated 180 degrees:

Here are the directions on the bottom of the box:






Symington's Puzzle, W. Symington & Co., Harborough, England, not dated.
(cardboard tray & sleeve, and four 1 inch cardboard cubes)
Same as instant insanity with red -> IDEAL TABLE CREAM (red), green->SOUPS (light blue), blue -> CUSTARD POWDER (white), white -> GRAVY (red with brown triangle), and cube 3 has the two hidden faces reversed:

Here are views of the top, front, and back (the bottom is the same as the top):





"Face 4" made by Ideal Toy Co. 1980.
(tray, cover, and four 1" pieces,
same as Instant Insanity with red -> green and green -> orange)


"Cube-4", except for name on cover is identical to Face-4.
(tray, cover, and four 1" pieces,
same as Instant Insanity with red -> green and green -> orange)
Hungarian "Bognar Buvos Golyok", patented by Jozef Bogner 1981 (GB2076663).




(4 inches long, 1" diameter, balls rotate in place, white / brown / black balls,
same as Instant Insanity with the 1234 order changed to 3142
and with red -> yellow, green -> red/orange, blue -> green, white -> blue)


Taktikolor, manufactured in Hungary, circa 1980?
(box and four 1.5 inch square plastic pieces with colored paper stickers,
same as instant insanity with green->red, white->yellow, red->green,
and for both cubes 3 and 4 the hidden faces are reversed)


Frantic, Wellingtons Ltd Stamford, UK, 1982.
(box and four 1.5 inch square plastic pieces,
same as instant insanity with green->red, white->yellow, red->blue, blue->green
and with hidden faces of cubes 3 and 4 reversed)


Diabolical, Wellingtons Ltd, Stamford, UK, 1982.
(package and four 1.5 inch square plastic pieces,
same as instant insanity with green->1, white->2, red->3, blue->4,
and with hidden faces of cubes 3 and 4 reversed)

Cat Puzzle, Copyright 1996 K. Miller / Images & Editions Stamford Lincs, England.
(cardboard box 4.25" x 4.25" x 1.5", solution sheet, and four 1.375" plastic cubes)
The box back and solution sheet are shown below. The solution is the same as instant insanity with the hidden faces of cubes 3 and 4 reversed, where red = "WIDE EYED CAT", green = "TABLE CAT", white = "TARTAN CAT", blue = "WHITE CAT" (the columns of the solution sheet correspond to cubes 1, 3, 4, 2):



Crazy Cubes, circa 1960's?



(four 1.25 inch square wood pieces labeled with whisky and numbers;
same as instant insanity with green -> 1, white -> 2, red -> 3, blue -> 4)
Sold solved with plastic over the pieces in a tray, with the directions on the back of the tray and the solution sheet under the pieces, where the cubes are arranged as shown in these photos (left is top and front, right is bottom and back):


By exchanging the right two cubes and then spinning each cube 180 degrees, the same presentation as for instant insanity on the first page is obtained:




Damblocks, Schaper Manufacturing Co., Minneapolis, Minn., 1968.
(package and four 1.2 inch square plastic pieces with colored paper stickers,
same as instant insanity with white->yellow)


Made by RainTree and purchased 2000.
(box and 4 pieces, each 7/8" inches square,
same as Instant Insanity with red -> green, green -> yellow, white -> red)


Made by Mr. Puzzle Australia and purchased 2005.
(tray and 4 pieces, each 1.5 inches square,
same as Instant Insanity with red -> circle, green -> Square, blue -> hexagon, white -> diamond)


Circa late 1800's?
(7/8 by 7/8 by 2.1 inch box with three identical 5/8" wood cubes;
original label on top was lost and replaced by a copy from an identical puzzle)
The Grand Army Of the Republic was a veterans organization formed after the American civil war (see the Wikipedia page). This puzzle has three identical cubes, each colored red, white, and blue on three pairs of adjacent faces. Like the four cube Instant Insanity puzzle, the object is to arrange the three cubes in a line so that each side has no duplicate colors. Below is a solution and its graph (constructed as for Instant Insanity); it is unique up to repositioning the puzzle and reordering the cubes (e.g., replacing cycle 2 by R - 3 - W - 1 - B - 2 - R is the same as rotating 180 degrees, rotating forward 90 degrees, and exchanging cubes 1 and 2):
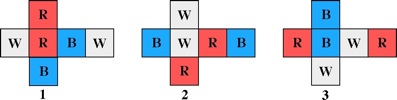
cycle 1: R - 1 - W - 2 - B - 3 - R
cycle 2: R - 2 - W - 3 - B - 1 - R
Further Reading
Wikipedia Page, from: http://en.wikipedia.org/wiki/Grand_Army_of_the_Republic


a.k.a. The Allied Flags Puzzle
Valentine & Sons, Ltd., Dundee, British Manufacture, circa 1918.
(1 x 1 x 4.4 inch cardboard box and five paper covered 13/16" wood cubes;
labels from Henry's of Manchester are on side and bottom of box;
similar in name and theme to the Allies Flags Puzzle)
The cube sides have flags from World War I (British, French, Belgian, Japanese, Russian). Like the four block Instant Insanity puzzle, the object is to arrange the five cubes in a line so that each side has no duplicate flags. Here are the directions that came with it:

Here are two solutions and their corresponding graphs (constructed in the same way as for Instant Insanity), where in the first both cycles use the same Hamilton path, but in the second the first cycle follows a different route:
Circa 1920's?




(left / right bottom: 2.15" x 2.7" x 1" box and 5 paper covered 3/4" wood cubes;
right top: 1.3" x 4.2" x 1" box and and same cubes as puzzle on left)
Similar in name and theme to the Allies Flag Puzzle, cubes have flags from World War I (U.S., British, Red Cross, Russian, Republic Of China). Like the Instant Insanity puzzle, the object is to arrange the five cubes in a line so that each side has no duplicate flags. Here is a solution and its corresponding graph (constructed in the same way as for Instant Insanity):

cycle 1: US - 1 - Russian - 4 - British - 3 - Red Cross - 2 - Republic Of China - 5 - US
cycle 2: US - 2 - Russian - 3 - British - 4 - Red Cross - 4 - Republic Of China - 1 - US



Made in Japan, undated.
(Cardboard box 1.6" x 1.4" x 5.5" with 4 1+3/8" wood cubes.)
In the theme of Instant Insanity, arrange the cubes in a row so that all four numbers appear on each side. Above is the solution and by numbering the cubes 1 to 4 going from left to right, the corresponding solution graph (unlike instant Insanity there are no colors, numbers are used to label both the cubes and the faces of the cubes).


Devised by Stephen Leslie, Copyright 1976 Onsworld Limited, England.
(four plastic cubes, clues and solution cards, cardboard box 1+5/8" x 1+5/8" x 6.5")
In a theme a bit like Instant Insanity, arrange the cubes so that all sides show an English word. Although the solution included has the letters in correct orientation on all sides, the directions do not say if it is allowed to have a letter on its side or upside down, and the letters, N/Z, U/C, H/I can be read differently depending on orientation. In the diagram above the letters on the outer and inside faces have their correct orientations, except the R and T on the right of the second and third cubes are rotated 90 degrees counterclockwise, and the D on the right of the fourth cube is flipped horizontally. Here are the "clues" and solution cards provided:




Here are the top and bottom of the box:


Here are the front and back of the box:



Made in the Czech Republic 1983.
(box and six 1.2 inch plastic cubes)
Each of the six cubes has a different one of the colors red, blue, green, yellow, white, and black on each side. This puzzle is similar to Drives You Crazy, but with a different color pattern. Like the four block Instant Insanity puzzle, the object is to arrange the cubes in a line so that each side has no duplicate colors. Here is a solution and its corresponding graph (constructed the same way as for Instant Insanity):

cycle 1: Y - 1 - B - 2 - G - 3 - W - 4 - BK - 5 - R - 6 - Y
cycle 2: Y - 4 - G - 5 - B - 6 - W - 1 - R - 3 - BK - 2 - Y

Purchased from Mefferts 2007.
(six 1.5 inch foam cubes)
Each of the six cubes has a different one of the colors red, blue, light blue, green, yellow, and orange on each side. This puzzle is similar to Iribako, but with a different color pattern. Like the four block Instant Insanity puzzle, the object is to arrange the cubes in a line so that each side has no duplicate colors. Here is a solution and its corresponding graph (constructed the same way as for Instant Insanity):

cycle 1: Y - 2 - G - 1 - O - 4 - LB - 6 - R - 3 - B - 5 - Y
cycle 2: Y - 3 - O - 6 - G - 5 - LB - 1 - B - 2 - R - 4 - Y
Note: W. Baeck has written a program to find six distict solutions, one being the solution shown above, and some employing two smaller cycles to form a solution half (1, 2, 3, 4, 5, 6).

Based on a puzzle produced in 1899; this version made by J. A. Storer, 2011.
(plastic box 1.5" x 2.5" x 3.3", instruction card,
and four 1+3/16" painted wood blocks with vinyl stickers)
Arrange the cubes in a 2x2 array so that all four letters appear on the top and bottom faces, all four letters appear on the left and right sides, and all four letters appear on the front and back sides. The letters are based on the names of two Boer generals, Joubert and Cronje, and two British generals, Buller and Warren, from an 1899 production of this puzzle.
We begin with a different puzzle; here the graph constructed as for Instant Insanity; we use letters to label faces and number the cubes 1 = green, 2 = red, 3 = brown, and 4 = yellow:
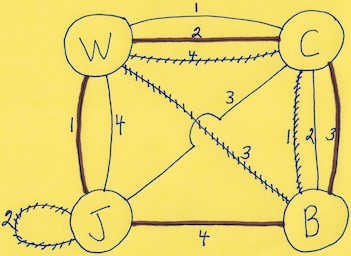
The two cycles, labeled by the thick edges and the hashed edges, give the following instant insanity like solution to arranging the cubes in a 1x4 array so that all for sides show the 4 letters; note that unlike the solution for instant insanity, one of the Hamilton cycles is actually a set of two cycles, a self loop and a cycle of three vertices:


cycle set 1: (J - 1 - W - 2 - C - 3 - B - 4 - J)
cycle set 2: (J - 2 - J) (C - 1 - B - 3 - W - 4 - C)
Solution idea: Unlike instant insanity, the graph of the preceding page does not give us a complete solution, because we cannot use disjoint cycle sets to simultaneously set both the top / bottom faces and the sides. Instead, we use each cycle set for a way to set the top / bottom faces that may lead to one or more complete solutions, by searching a new graph that describes the ways that cubes can be in a 2x2 array without changing the top / bottom faces. These secondary graphs are constructed below by going around the sides of each cube in a clockwise direction, where when we go from face X to face Y, we place a directed edge (an edge with an arrow) from vertex X to vertex Y (a total of 16 edges). We now look for cycle sets, but with the rule that the direction of arrows must reverse when going from one cube to an adjacent cube, or stay the same when skipping a corner (that uses a self-loop) and going to the opposite corner.
Solutions based on cycle set 1: Cubes 1 (green) and 4 (yellow) form self-loops; if they are adjacent then the red and green edges can be used to cycle between cubes 2 and 3, and if they are diagonally opposite, then the red and blue edges can be used to cycle between cubes 2 and 3. In both cases, and alternate solution can be formed by exchanging cubes 1 and 4:
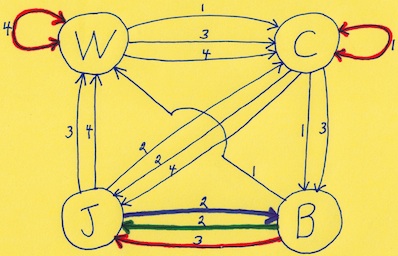


Solutions based on cycle set 2: We find a solution based on self-loops for cubes 1 and 4 when they are diagonally opposite (and an alternate solution exchanges cubes 1 and 4):
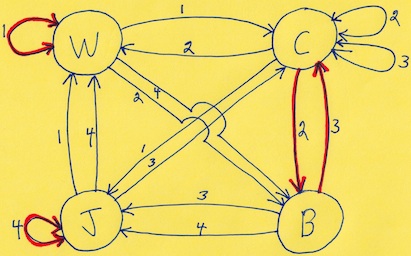

Further Reading
Boer Wars Wikipedia Page, from: http://en.wikipedia.org/wiki/Boer_war


Patented by Jozef Bogner 1981.
(white / brown bodies, 1.7 inches)
Bolygok means planets in Hungarian. A generalization of the Hungarian version of Instant Insanity ("Bognar Buvos Golyok"). Rotate the balls to make patterns such as each side with all four colors or each side with the same color. The directions that come with it are in a long strip; here are pieces of it:

Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/bolygok.htm
Bognar UK Patent Application, GB 2,076,663.

KMS Industries, Alexandria, VA, 1968.
(plastic, 1.75 inches;
directions are in the bottom)
Take the eight cubes out of the case and arrange them in a single 2x2x2 cube to make different patterns. The cubes have one of the colors red, blue, green, and white on each face. The card that is in the bottom of the cage challenges give a number of challenges, including making each face showing all four colors:



KMS Industries, Alexandria, VA, 1968.
(plastic, 1.75 inches;
directions are in the bottom)
Each of the eight cubes has three colored rods going through it, one in each of the x, y, and z directions (four of the cubes have a red, blue, and white rod, two of the cubes have two reds and a white, one has two reds and a blue, and one has two whites and a blue). Take the eight cubes out of the case and arrange them in a single 2x2x2 cube to make continuous rods of the same color passing through it:




Handle says "Clementoni"; unknown date of manufacture.
(plastic with paper surfaces, 12 pieces, 6 by 6.5 by 1.75 inches)
Position the blocks to make a Disney scene. Newer puzzles of this type are shown on the 2008 Clementoni web page (www.clementoni.com) as their 12 piece "super color cubes".



a.k.a. Spots Puzzle
St. Pierre & Patterson Mfg. Co. 1957.
(cardboard tray and nine 2 x 5/8 inch wood bars with recessed white dots;
shown as the "Spots Puzzle" on pages 98-99, 130-131 of the 1893 Hoffmann book)
Assemble nine 1x1x3 unit bars into a die; from left to right in the photo above, the dots are:Here are close-up views of portions of the back of the box:
1. no dots
2. left end
3. top center
4. top center
5. top left, end right6. top left & right
7. top left & right, end left & right
8. top left & right, end left & right, front right
9. top left & right, end left, front left & right









Pentangle Puzzles And Games, England, 2009.
(plastic box and 9 L-shaped wood pieces, 1+7/8 inches)
Assemble the nine L-shaped pieces into a die, with either legal green spots on the outside or legal red spots. Sold in the green solution, which is a "right-handed" die; the red solution is a "left-handed die". Directions tell how to get a "Certificate of Failure". Here are photos of two stages of taking these two solutions apart:





Copyright Warner Brothers 1992.
(wood base and 8 blocks, 4 inches)
Slide the 8 blocks onto the 4 posts to make a 2x2 cube so that each of the 4 sides shows a single character. Below are photos of the other two solved sides and the blocks arranged to show the 8 distinct characters used (each block has some combination of 4 of these): Tweety Bird, Bugs Bunny, Road Runner, Daffy Duck, Marvin the Martian, Sylvester, Wile E. Coyote, Taz (Tasmanian Devil).



Copyright 2003 & Design Patent 2006 by Use Your Head Unlimited.
(plastic, base + top + 10 pairs of 1" diameter balls)
There are 10 pairs of colored balls, one pair for each of the possible pairs of the five colors white, yellow, orange, pink, and blue:

These pairs must be placed to form a pyramid so that no two balls of the same color are touching. The directions say that you should also not allow the same colors to touch as you are building, even for places that are not visible when the puzzle is completed. This is a relatively easy puzzle that is fun for children. It has more than one solution. The puzzle pictured here is the golf version; the same puzzle has also been advertised / sold with other sports themes (soccer, baseball, basketball, tennis, football).
The manufacturer has filed a number of design patents relating to this puzzle and its junior version. P. Roberts and A. Kuwagaki & S. Takenaka have 1970's patents on pyramids using pieces formed from more complicated arrangements of balls.
Further reading:
Thompson Design Patent, from: www.uspto.gov - patent no. D524,381
Roberts Patent, from: www.uspto.gov - patent no. 3,945,645
Kuwagaki Patent, from: www.uspto.gov - patent no. 3,837,652

Copyright 2000 & Design Patents 2005 by Use Your Head Unlimited.
(plastic, base + top + 5 pairs of 1" diameter balls
There are 5 pairs of colored balls, using the colors white, yellow, pink, and blue (all of the 6 possible combinations except pink-blue):

These pairs must be placed to form a pyramid so that no two balls of the same color are touching. The directions say that you should also not allow the same colors to touch as you are building, even for places that are not visible when the puzzle is completed. This is a relatively easy puzzle that is fun for children; it has fewer pieces that the Smarts Puzzle 4 high pyramid made by the same company. It has more than one solution. The puzzle pictured here is the golf version; the same puzzle has also been advertised / sold with other sports themes (soccer, baseball, basketball, tennis, football).
Further reading:
Thompson Design Patents, from: www.uspto.gov - patent nos. D500,533, D500,534, D500,535, D500,816.

Probably made in Hungary in the 1980's.
(plastic, 3.5 inches)
Made by Tantrix, purchased 2007.
(3 inches)
Rotate the hexagonal and square faces so that the edges match. Fairly easy to solve because by starting at one vertex where three faces meet, there are not many possibilities, and then you can start working your way around. The bottom face of the Hungarian version is plain black. The faces of the tantrix version ("The Rock") can also be snapped off and put on in different positions to make different puzzles.
The 1983 patent of Sasso describes a similar idea for a regular solid shape where pairs of opposite faces rotate together.
Further Reading
Sasso Patent, from: www.uspto.gov - patent no. 4,416,453

Patented by REFO Verlag GmbH 2002.
(plastic, 2.6 inches)
Turn the 6 rings so at each of the 12 places they meet the colors match. This is a slightly simpler and more colorful version of the Turn 12 puzzle that as 24 numbers on each ring (each in the range 3 to 9, where matching is by adjacent numbers summing to 12 - see Jaap's Page). Here are the directions that came with the puzzle:

Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/turn12.htm
REFO DE Patent, from: www.epo.org - patent no. DE20112728

Patented by Rubik 1991, copyright Matchbox 1990.
(3.5 inches)
When assembled, the four sides of the pyramid are red, blue, yellow, and white. Moves consists of unsnapping a portion rotating it and snapping it back on.

Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/triamid.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/r90/trmd0.htm
Rubik HU Patent. from: www.epo.org - patent no. HU207233

Although cubes and various types of burrs are common shapes for assembly puzzles, beautiful craftsmanship, often from wood, has gone into puzzles of many geometric shapes. Well known work on geometric puzzles going back to the 1970's has been by Stewart Coffin; see for example his book The Puzzling World of Polyhedral Dissections, as well as his Ap-Art book that catalogs the many puzzles he has made. See also the books of Greg Frederickson, including Dissections Plane and Fancy and others. Rhombic Polyhedra Puzzles Part 1 and Part 2, by George Bell and Stephen Chin, documents some of the beautiful work by Interlocking Puzzles in the 1980's. Some geometric puzzles employ coordinate motion (a term used by Stewart Coffin) where pieces must be slide together simultaneously when assembling; for example see the Three Pairs puzzle..

Patented E. Johnson 1940, David Co. circa 1990's?, lower right circa 1960's?.



(top: 3.5"x2.7"x1.4" box, two 3" wood pieces, and directions;
lower right: 2.5"x1.75"x1/2" plastic box and two plastic pieces)
Further Reading
Johnson Patent, from: www.uspto.gov - patent no. 2,216,915


Designed by Wayne Daniel, made and sold by Interlocking Puzzles 2002.
(Jarrah, 3 pieces, each edge 3.5 inches when assembled)

Box says "MADE IN U.S.A. S.K. & CO.", circa 1950?
(cardboard box and 4 wood pieces, 2.5 inches)
Like the classic Two Piece Pyramid where each piece has been cut in half. Here are photos of it being assembled:







Designed by W. Schneider, copyright Binary Arts, 1998.
(4 identical plastic pieces, 3.25 inches on a side when assembled)



Designed by Wayne Daniel, made and sold by Interlocking Puzzles 2002.
(Jarrah and Maple, 4 pieces, each edge 4.75 inches when assembled;
as shown above, comes apart into two 2-piece assemblies)

Designed by Wayne Daniel, made and sold by Interlocking Puzzles, 2003.
(Paduk and Maple, 4 pieces, 3.5 inches)
Two pairs of identical pieces slide together simultaneously. The solved puzzle has a maple diamond on each face where one point meets the point of a diamond on an edge shared with an adjacent face. Here are views of the start of coming apart, and the four pieces:


To solve, as shown on the left below, determine how to assemble two halves that are in the solved state, spread each apart to just coming apart, and with one par in each hand position carefully so that everything can be pushed together. The photo on the right below shows the side not shown in the photo at the top of this page.





Designed by Wayne Daniel, made and sold by Interlocking Puzzles 2002.
(Jatoba and Maple, 5 pieces, each edge 6 inches when assembled;
as shown above, comes apart into a 3-piece and 2-piece assembly)


Designed by Steve Smith, made and sold by Interlocking Puzzles 2004.
(sequential assembly version: Maple, 4 pieces, 3.5 inches,
simultaneous movement version: Jarrah, 4 pieces, 3.5 inches)
These two puzzles have the same size and shape, with six square faces and eight hexagon faces; they were both designed by Steve Smith of Interlocking Puzzles (Interlocking Puzzles also made a third easer puzzle of the same size and shape that was designed by Wayne Daniel). The one on the left above requires sequential assembly of the four pieces in a specific order. The one on the right requires all four pieces to move simultaneously. Here is some of what the designer said about this simultaneous movement and a photo of the puzzle coming apart:"All four pieces must move simultaneously; there are two pairs of mirror image pieces made from Jarrah. There are 4 "solid" faces where the entire face is part of the same piece and four "multi' faces where the face has sections from three different pieces. Two of the multi faces (which are opposite each other) have a triangular shaped section, a diamond shaped section, and a trapezoid shaped section (the other two have two triangular sections and one larger non-convex section); by holding on to these two faces you can push the puzzle apart (all eight faces remain parallel as the puzzle expands)."



a.k.a. Cuboctahedron
Designed by Steve and Leslie Smith, made and sold by Interlocking Puzzles 2004;
box made by J. A. Storer 2004.
(5 pieces: Jatoba, 4.5 inches,
6 pieces: Peroba Rosa, 4.5 inches,
7 pieces: Jarrah, 4.5 inches,
box is 3/8 inch plexiglass with metal hardware, 5 by 5 by 12 inches)
These three puzzles have the same size and shape, with six square faces and eight triangular faces (corresponding to where the corners of the cube have been truncated). The five piece version was designed by Steve Smith and the 6 and 7 piece versions by Steve and Leslie Smith. Here is some of what they say about these three puzzles:Five piece Truncated Cube: "Each piece is a challenge, even after removing the first three, getting the last two apart and together isn't easy. Reassembly? Let's just say this should NOT be the first polyhedra puzzle of ours you work with."
Six piece Truncated Cube: "A small internal space requires multiple moves to get the first piece out."
Seven piece Truncated Cube: "Unique trilateral symmetry makes this puzzle quite difficult. This puzzle can be thought of as two three piece puzzles, with a key piece that holds it all together."

Designed by Stewart Coffin, purchased from Cubic Dissection 2004.
(wood, 6 pieces, 2.5 inches)



Purchased from Toys From Times Past, 2014.
(3 identical pieces, each made from 4 3/8" thick parallelograms;
when assembled 3" side to side, 1.5" high)
A first the pieces seem locked together. The pieces move simultaneously to disassemble, and the trick is to push on the top layer in the correct way to spread them apart:





Designed by Khono Ichiro, made by Eric Fuller 2021.
(Canzan wood with magnets, each block 1" square x 1/2" thick)
Three pieces, each formed with two 1" x 1" x 1/2" half cubes with little magnets in their center, snap together to form three 1" cubes. Fun and easy to solve by trial and error to get the magnets to line up properly.

Designed, made, and sold by Stewart Coffin in 1970's and early 1980's.
(mahogany, 3 pieces, 4 inches;
one of 6 puzzles purchased during a visit with the designer in the early 1980's)
Described in Stewart Coffin's book The Puzzling World of Polyhedral Dissections; here is some of what he says in the directions that came with the puzzle:"The one symmetrical face of the assembled puzzle happens to resemble a certain corporate logo. The company wanted a simple puzzle incorporating this pattern for some sort of promotional scheme. So the arrangement of six of the blocks was already determined. All that was required to complete the design was the addition of four more blocks in a sort of triangular pyramid and a judicious choice of glue joints to make it into an interesting interlocking puzzle. So the company got what they wanted - except for one thing. It turned out to be anything but simple!"When apart, it is hard to visualize what it is supposed to look like when assembled (although once assembled, you know you have it). Here are photos showing the piece orientations for assembly and the first of the two steps that puts together the two three block pieces:



Vin & Co., purchased from Bits & Pieces 2007.
(wood, 6 pieces, 3.5 inches)
Here are the directions and solution that were sold with the puzzle:
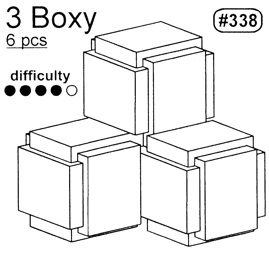


Designed and made by Stewart Coffin, 1997.
(wood, 3.25" by 1.75" high, each pod is 1.5" between parallel faces;
written to the right of the International Puzzle Party sticker
is the designer number / signature / date)
Three pieces come apart with simultaneous movement:




Designed and made by Stewart Coffin, 2010.
(wood, 3.25" by 1.75" high, each pod is 1.5" between parallel faces;
signed on the inside;
one of 4 puzzles purchased during a visit with the designer in 2014)
The name of this puzzle appears to come from the Three Bunnies puzzle, which has the same size and shape and is 118 in the author's new numbering system in the Coffin AP-ART book.


Designed, made, and sold by Stewart Coffin in 1970's and early 1980's.
(left: Mahogany, 6 pieces, 4 inches
right: Cherry, 6 pieces, 4 inches;
the one on the left was purchased at auction in 2001, the cherry one on the right is
one of 6 puzzles purchased during a visit with the designer in the early 1980's;
he called this cherry one a "crude loose-fitting prototype",
but of course it has terrific fit, and although it has some nicks
and pencil marks on the interior edges, overall it is a beautiful puzzle)
Described in Stewart Coffin's book The Puzzling World of Polyhedral Dissections; here is some of what he says in the directions that came with the puzzle:"To disassemble, grasp the opposite pairs of pieces, and gently pull and wiggle until you discover the combination that separates it diagonally into halves. The wiggle the pieces apart until you discover the strange action that separates each half into three pieces."The name is a joke that implies that each of the three axes is formed from some sort of pair configuration; that is, the implication being that the puzzle works something like a burr, where pieces slide in and out parallel to the three axes. In fact, it splits into two halves of 3 pieces each along a diagonal plane. Then, the two halves each come apart by simultaneous motion of all three pieces. Below, the left shows the two halves and the right shows one of the pairs:



Designed, made, and sold by Stewart Coffin in 1970's and early 1980's.
(Cherry and Rosewood, 6 pieces, 4.5 inches;
one of 6 puzzles purchased during a visit with the designer in the early 1980's)
Described in Stewart Coffin's book The Puzzling World of Polyhedral Dissections; here is some of what he says in the directions that came with the puzzle:"The Augmented Four Corners Puzzle consists of six dissimilar interlocking pieces which assemble in one way only, with one sliding axis, to form a geometrical solid with tetrahedral symmetry."Use the three pieces shown below to put together the top (shown with a rubber band) so that the "legs" that hang down have vertical sides that will slide down onto the other three pieces.


Design Science Toys LTD, Tivoli, NY, circa 1990's?
(wood with magnets, 4 inches)
Wood pieces with magnets, each in the shape of a rhombic hexahedron (a slanted cube), can be assembled into shapes, including the same shape as the Augmented Four Corners puzzle. The sheet that comes with the puzzle motivates the use of these pieces from the angles found in carbon molecules.


Designed, made, and sold by Stewart Coffin in 1970's and early 1980's.
(Rosewood and Tulipwood, 6 pieces, 4 inches;
one of 6 puzzles purchased during a visit with the designer in the early 1980's)
Described in Stewart Coffin's book The Puzzling World of Polyhedral Dissections; here is some of what he says in the directions that came with the puzzle:"This puzzle has the most unusual capability of being assembled into three different symmetrical solid shapes, even though its six pieces are all identical in shape."Four assembled shapes are shown in Stewart Coffin's book Geometric Puzzle Design; where he discusses the 4-piece Fusion Confusion; version of this puzzle. One shape is the "star" shown above (6 points running vertically); below are two ways to pull it apart into two sets of three pieces. Another is the "hex ring" (a vertical hexagonal cylinder with a ring around the middle) that is show below, and to its right a way to pull it apart. Note that rubber bands have been used in these figures to hold pieces in place while photographed.





Designed by Stewart Coffin, made by interlocking puzzles 2001.
(Paduak and Guatam, 4 pieces, 3.3 inches)
The four pieces of this puzzle are formed by joining two pairs of the six pieces of the Triumph puzzle. Triumph is described in Coffin's book The Puzzling World of Polyhedral Dissections, and this puzzle is described in his book Geometric Puzzle Design, where he says that it has all of the original four solutions of the original Triumph puzzle, but with "only one confusing diagonal axis of assembly". To make the star shape, first join two pairs, and then slide the two halves together:



Designed, made, and sold by Stewart Coffin in 1970's and early 1980's.
(Mahogany, 6 pieces, 4 inches;
one of 6 puzzles purchased during a visit with the designer in the early 1980's;
handwritten on the directions Stewart Coffin says "second, nicks and scratches, poor fit";
of course, as you would expect, the puzzle looks great and has a good fit)
Described in Stewart Coffin's book The Puzzling World of Polyhedral Dissections; here is some of what he says in the directions that came with the puzzle:"Examine the six individual puzzle pieces and note that there are three identical pieces which we shall arbitrarily refer to as "left-handed" pieces, and three right-handed pieces likewise identical except that one of them has a tapered hole with a pin stuck into it. To assemble the pinwheel solution, first remove the pin and set it aside. Sub-assemble the three left-handed pieces into one sub-assembly, and the three right-handed pieces into another, and mate the two halves. The resulting solution has an axis of symmetry. The other symmetrical solution, known as the Rosebud solution, requires the simultaneous manipulation of all six pieces."

Designed by Stewart Coffin, made by interlocking puzzles 2002.
(Peroba Rosa, 12 pieces, 5 inches)
In Geometric Puzzle Design, Stewart Coffin says: "Twelve sticks of triangular cross-section with pyramidal end blocks assemble with some difficulty to form a symmetrical interlocking burr." Here is the solution that was sold with the puzzle (pieces are numbered in assembly order):
Step 1: Assemble pieces #1, #2, and #3 to form a triangular base.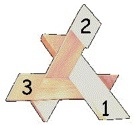
Step 2: When in place piece #4 will stand vertically with piece #5 parallel to piece #3. Piece #5 is the only piece with an extra augmentation. Assemble with the augmentation directly to the left of piece #2. Hold #4 loosely to allow #5 to slide in under the hook of #2.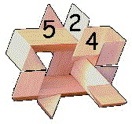
Step 3: When in place piece #6 will be parallel to #4. To assemble, piece #6 hooks around #2 from below and slides up through next to #4.
Step 4: When in place piece #7 will be parallel to piece #1. To assemble, first push piece #1 all the way into the puzzle. This allows piece #3 to move to the left giving room for piece #7.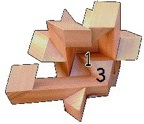
Step 5: Insert piece #7. Slide piece #3 back to the right and #1 forward.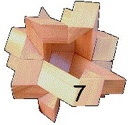
Step 6: When in place piece #8 will be parallel to piece #2. To assemble, place #8 on the right side by hooking around #4 and sliding through #1.
Step 7: Now the puzzle has enough pieces in place to hold together better. When in place piece #9 will stand vertically, parallel to piece #4 and #6. To assemble, drop #4 down and move piece #7 back away from you. Bring #8 towards you until enough opening is made to allow for #9.
Step 8: Insert #9 by hooking around #3. Push #8 back in place to allow #4 to come back up. Make sure #9 is all the way down to allow #7 to slide back towards you. Bring #9 up to its final place. When in place piece #10 is parallel to #5 and #3. To assemble, hook the end of #10 around #8 and slide left under #9.
Step 9: When in place piece #11 is parallel to #8 and #2. To assemble, first drop #4 and #6 down. Slide #8 all the way towards you. Then move #10 to the left just enough.
Step 10: This allows #11 to be inserted underneath #10 with its end hooking around #7. Slide #10 back to the right. Now #8 slides back to allow #4 up. Make sure #11 is all the way towards you to allow #6 to come back up.
Steps 11 & 12: Move #11 to its final place. Then the key piece #12 moves in parallel to #7 to touch the augmented place on #5.


"Crystall Pyramide", made in China, purchased 2009.
(15 wood pieces and base, 5.75 by 5.75 by 3.5 inches high)
Pieces formed from wood rods glued together must be placed on a base (that has some black rods glued to it) to form a pyramid; here is the solution that was sold with the puzzle:
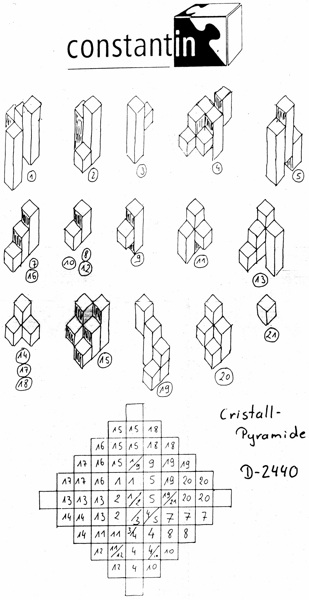

Patented K. Walker & designed with H. Nelson, made by Binary Arts, circa 2000.
(four plastic pieces, 4 x 4 x 3/4 inches assembled)
The four pieces do not simply come apart as it appears they might; careful positioning and twisting is required; here is the solution that was sold with the puzzle:
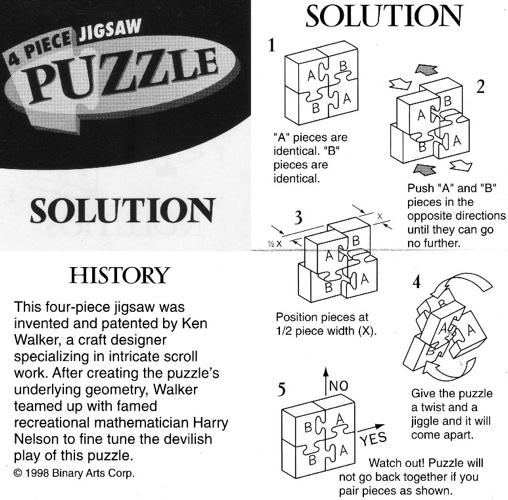
Further Reading
Walker Patent, from: www.uspto.gov - patent no. 5,409,227

3D print design by Hvmhvm, http://www.thingiverse.com/thing:1645742, 2016.
(fabricated on a Monoprice V2 printer in 2021,
PLA plastic, scale 95%, infill 22%, resolution 0.175mm,
four pieces, assembled printed size 1.5" square)
Here are the other three sides of the assembled puzzle:

The pieces can be paired in either of two ways, and then the two halves slide together:
-> ->


B. B. Shackman & Co., New York, circa 1940?
(wood, 1.7 by 1.7 by 2.9 inches; end not shown says "MADE IN U.S.A.)

Unknown maker, circa 1930's?
(wood, 3/4 inches square by 3 inches long)
A simpler 3x3 version (3 wavy horizontal cuts and 3 wavy vertical cuts) of the 4x4 puzzle described on page 109 of the 1893 Hoffmann book.

From the grandfather of J. A. Storer; circa 1900?
(wood, 2.4 by 2.75 by 1.9 inches)
A simpler 3x4 version (3 wavy horizontal cuts and 4 wavy vertical cuts) of the 4x4 puzzle described on page 109 of the 1893 Hoffmann book.






Made in Japan, circa 1960's?
(wood, 1+7/8 inches)

Received as a gift from D. Storer, 2005.
(Cherry, 12.5 inches assembled)
Pull out the white peg that goes through to make the eyes, and the puzzle comes apart in a mor or less linear fashion; about midway through there is a small compartment containing a wood duck:


Designed by Oskar van Deventer, made by Eric Fuller 2010.
(Pau Ferro and Quilted Maple, 3 inches)
Five pieces, each composed of the shape of a matchbox cover attached to a matchbox tray assemble to a single shape. Here are the pieces:

The two pieces on the top left slide together, then as shown below the pairs of vertical pieces slide together (and the third step slides the two halves together):



Purchased from Puzzles and Brain teasers EBay Store 2007.
(wood dowel and 6 wood pieces with dowels, 2.75 inches;
shown on Page 70 of Coffin's Book on Polyhedral Dissections)
Six wood pieces with pegs and a key peg (the key peg has a little pin to make friction so it does not fall out of the solved puzzle). Here are solution steps:








Purchased 2006.
(Walnut and Oak, 8 pieces, 5 inches by 3/4 inches thick)
Assemble three pairs and then push together simultaneously:



Purchased from Mr. Puzzle Australia 2006.
(wood, 11/16" cubes, 2.75" x 3.5" x 2" when assembled)
This puzzle is constructed like Kev's Cubes. Here, 31 wood pieces (30 unit sized cubes and one 1x1x2 piece) are connected by an elastic cord, and must be manipulated into the shape shown in the photo above.


Circa 1980's.
(plastic, 4 inches as assembled above)
A sequence of linked plastic pieces that can an be folded into fun shapes. The "solved" position is a 3D diamond shape shown above that fits into the plastic ball in which the puzzle was sold.
Further Reading
Rubik's Snake Booklet, from: http://www.rubiks.com/World/~/media/Files/hint_snake.ashx
McFArren's Page, from: http://www.geocities.com/abcmcfarren/math/snake2d.htm
McFarren's 3D Page, from: http://www.geocities.com/abcmcfarren/math/snake3d.htm
Wikipedia Page, from: http://en.wikipedia.org/wiki/Rubik's_Snake

Sold by Bits and Pieces 2007.
(aluminum, 4 pieces, 2.5 inches)
Four aluminum pieces fit together; here are four basic solution steps:
Step 1: Identify the two pairs:

Step 2: Put the left pair together:

Step 3: Add the third piece:

Step 4: Slip on the fourth piece:



a.k.a. Construction Cigar, Cigar Puzzle
Garner Products and Shackman & Co., New York; this one for sale in 1950's.
(wood pieces on metal rod with 6 short rods, 5.2" long x 3/4" diameter)
This puzzle was purchased from a seller who said that it came from residual stock of Glenn's Novelty Shop, 16th and Market St., Philadelphia, where his father worked when the shop closed shop in 1959. Subsequently puzzle collector Michel van Ipenburg kindly provided a copy of the Garner directions and puzzle collector Bill Ja kindly provided a copy of the Shackman directions and also sent a much appreciated gift of a set of reproduction short rods (that were missing from this one). Both directions, shown on the following pages, show these objects to make:
Chinese
Lantern
Knife
Grinder
HotWater
Bottle
Fire
Siren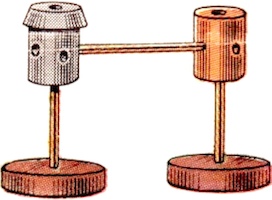
Hitching
Post
Urn On
Pedestal
The short rods are stored in the middle brown tube; from left to right in the photo above, on the left below is a photo of the left ends of the tubes and on the right a photo of the right ends:



Circa 1960's.
(plastic, 2.75")
These keychains, barely a puzzle, became popular in the 1960's and have been made over the years for numerous objects, animals, shapes, etc. over the years. Here are three more examples and the directions that came with them:

(1.75" high)

(1.8" long)

(1.75" high)




Circa 1950's.
(plastic, 3.25" high by 2.25" diameter)




3D print design by G. Frost, http://www.thingiverse.com/thing:26334, 2012.
left: fabricated by L. Milekic 2016, PLA plastic, 2" x 2" x 1.5", 2018;
middle: fabricated on a Monoprice V2 printer, PLA plastic, 2" x 2" x 1.5", 2019;
bottom: fabricated at scale 135x, PLA plastic, 2.75" x 2.75" x 2", 2019)




Referring to the two color version, the two white pieces are the same shape but are not quite the same dimensions. Similarly, for the two dark pieces (that are symmetric to the white pieces). So first match each white with its corresponding dark piece. The two white pieces slide together on one plane and the two dark pieces slide together on a perpendicular plane. Start by putting three together and see how the fourth fits in. Then spread them all apart just right with the fourth piece now in position, and push together with simultaneous movement. Takes a bit of dexterity.

The great thing about the classic Rubik's Cube is that you don't have a bag of pieces when it is unsolved. Keep it on a coffee table, pick it up, play with it, and put it down when get tired. The original 3x3x3 Rubik's cube started an entire class of manipulation puzzles.

First patented by Rubik 1983, other patents cover different internal mechanisms.
(plastic, 1.5 inches)
Rubik 2x2x2 Three Step Solution
Notation: L (left), R (right), F (front), B (back), U (up), and D (down) for 90 degree clockwise rotations of that face, - means counterclockwise. Corners are named with three letters.
1. Solve the down layer.*** No need to remember sequences; after playing with the puzzle it becomes easy. Get three corners correct, move two of the correct ones 90 degrees, move the fourth into position, and move the two back. If the 4th is rotated so it won't position correctly, do a 180 degree turn of that side and then you can reposition it to try again.2. Put the up layer corners in correct locations (but possibly rotated incorrectly):Use the following sequence exchange two corners:3. Fix the up layer so all corners are rotated correctly:
FLU <-> FRU: ( F U ) (F- U-) (L- U- L)
Note: A quick way to do UBL <-> UFR is to precede this by L and skip the final L.Position the cube so the up front right corner is not correct and repeat these two steps until all up corners are correct:
- Repeat until the up front right corner is correct:
(R- D-) (R D)
*** The down layer will be mixed up, but it will become correct again at the end; don't forget the final D of this sequence.
- Rotate the up layer so the up front right corner is not correct.
Notes About The Rubik 2x2x2 Three Step Solution
Step 2 - an easier but slower solution: This step could be replaced by:Step 2. If possible, rotate the up layer to be correct, except some corners may by be rotated; otherwise, mix up and go back to Step 1 using a different color on the bottom.Step 2 - making it faster: This step can be used three times for a diagonal exchange. However, since it does not change the upper back left corner, it is faster to do UBL <-> UFR by preceding the transformation with L and skipping the final L.
(Starting from a random position, there is a 1 in 6 chance that this test succeeds. So even if a quick mix and starting with a different bottom is not completely random, once you get reasonably fast at doing Step 1, it shouldn't take too long.)
Step 2 - using a Rubik 3x3x3 move: The "corner cycle" move of a Rubik 3x3x3 solution can be used for this step.
Step 3 - making it faster: Every iteration of the corner rotator exchanges UFR and DFR, and repeating it 6 times returns the cube to exactly where it was. Step 6A will use the corner rotator 2 times if the top color is on the right side of the UFR corner, but 4 times if it is on the front, in which case it is faster to do the reverse sequence 2 times:reverse corner rotator: D- R- D RStep 3 - why it works:
- Step 3A affects only 4 corners by exchanging the two front right corners and also exchanging the two back down corners.
- Doing Step 3A twice leaves corners in the same positions, except those four corners are rotated, and doing Step 3A six times leaves the corners the same as when you started.
- On the up layer Step 6 only modifies the front right corner.
- Since Step 3 started with the down layer correct, once three of the four up corners have been fixed, fixing the fourth up corner must leave the down layer correct. This is because when at every 6th move the two back bottom corners are correct, all that is left that could be incorrect are the two front right corners, but due to parity considerations, a completely solved puzzle except for two adjacent rotated corners is not possible.
- This transformation also works for a Rubik 3x3x3 cube (and is the last step of the layer by layer solution presented on that page). The only edge pieces that are affected are FR, RD, BD, which are on the lower two layers; they return back to where they were after 6 moves.

Step 1. Solve the down layer.
Step 2. If possible, rotate the up layer to be correct, except some corners may by be rotated; otherwise, mix up and go back to Step 1 using a different color on the bottom.
Step 3. Fix the up layer so all corners are rotated correctly:Reposition the cube so the up front right corner is not correct, and repeat these two steps until all up corners are correct:
- Repeat until the up front right corner has the correct color on top:
(R- D-) (R D)
Where R and D mean to rotate the right and down layers 90 degrees clockwise, or R- and D- mean to rotate the right and down layers counterclockwise.
- Rotate the top layer 90 degrees counterclockwise.

(From the booklet that came with Rubik 2x2x2 Homer Simpson.)
Step 2:FRD <-> BLD: F L D L- D- F- D- ("diagonal swapper")Step 3:
FRD -> BLD -> BRD -> FRD: B L D L- B- L D- L- ("shunter")FRD-, BRD-, BLD-: R- D- R D- R- D2 R D2 ("shifter")
Call Step 3A S and its reverse S-:S = (R- D-) (R D)Consider interleaving a do-nothing sequence of U's into a do-nothing sequence of S's:
S = (D- R-) (D R)
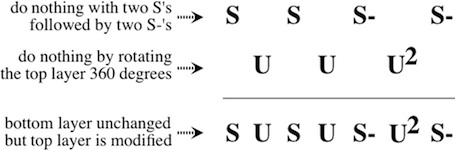
Here is how this sequence cycles three corners A,C,D on the top layer (and the cube is returned to where it was if you do it three times), or if it is followed by a U, it exchanges two corners B and C on the top layer (X denotes the corner below A at the start):
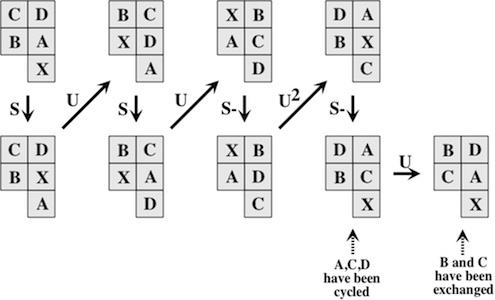
Notation: R (right), F (front), and D (down) for 90 degree clockwise rotations of those faces, and - for counterclockwise instead of clockwise. A 2 means do it twice. Corners are denoted with three letters (e.g., BLD = back left down corner).
Sequences for exchanging corners:FLD <-> FRD: F D F- D- R- D- RSequences for rotating corners (+ / - denote clockwise or counter clockwise):
FRD <-> BRD: R F D F- D- R- D-
(Jaap's page does FRD <-> BLD: F- R- D- R D F D- )FLD-, BLD+: R- D- R F- D R- D R D2 F2These transformations are done from the point of view of the top layer solved and then solving the bottom layer, because it makes the puzzle easier to hold with the left hand and manipulate with the right hand (no moves of the up, left, or back layers needed).
FLD+, BLD-: F2 D2 R- D- R D- F R- D R
FLD-, BRD+: R2 D- R D2 R- D2 R D- R2 D
FRD-, BRD-, BLD-: R- D- R D- R- D2 R D2
FRD+, BRD+, BLD+: D2 R- D2 R D R- D R
FRD-, BRD+, BLD-, FLD+: R2 D2 R D2 R2 D
FRD+, BRD-, BLD-, FLD+: R D F R2 D2 F2 D F- D R2
Jaap's Page presents the above transformations along with many more, including transformations to make specific patterns.


Plastic, stickerless, made in China, purchased from Amazon.com in 2015.
(DaYan, sold by Maxin, comes in a fitted box, 1.8" square)
In the early 2000's, smoother working versions of Rubik's 2x2x2 were widely available, with screws / springs for adjustable tension and smooth turning even when layers are not exactly aligned (beveled interior corners in conjunction with the spring action give a minimal degree of automatic alignment). Even dimension Rubik cubes, of which the 2x2x2 is the smallest, don't use a central axis like standard odd dimension designs such like the Rubik's 3x3x3 cube. Here are photos of the one shown above apart:



The Darth Maul figure is large (4 inches high) with a smooth mechanism. The others are small (between 2.25 and 2.5 inches high) from Kellogg's cereal boxes in the 2002 time frame; each has two related star wars episode II figures, one on each side.

Darth Maul

Darth Vader / Anikin Skywalker

Obiwan Young / Obiwan Older

Lea / Amidala

Dooku / Emperor

Trooper / Jango

R2D2 - C3PO

Homer Simpson
(circa 2000, 5")
Bart Simpson
(circa 2000, 4.5")


Dog, Kitty, Penguin
(China, 2006, all three are 4.25")
Jaap's Page, from: http://www.jaapsch.net/puzzles/cube2.htm
Rubiks.com booklet, from: http://www.rubiks.com/World/Rubiks%20downloads.aspx
Rubiks.com assembly diagram, from: http://www.rubiks.com/World/Rubiks%20downloads.aspx
Rubik Patent, from: www.uspto.gov - patent no. 4,378,117
Li Patent, (Eastsheen Mechanism), from: www.uspto.gov - patent no. 5,826,871
Patermann EP Patent (Mickey Mouse), EP712,649.
Khoudry International Patent (K-Ball), IP25874.
Kremmer Patent (Darth Maul), from: www.uspto.gov - patent no. 6,217,023
Nicholas Patent (uses magnets), from: www.uspto.gov - patent no. 3,655,201


Patent filed by Erno Rubik 1975, sold by Ideal Toys in the 1980's.
(plastic with colored stickers, 2.2"; keychain 1.2")
The first puzzle of this type in a large class of puzzles in the years to follow. Challenging and fun to play with. A number of ways to construct this puzzle have been devised over the years; here are the pieces of an original Rubik's Cube like shown above, where there is a central axis assembly and 20 pieces that interlock with it.

- Solve the top layer (including its sides) and turn the cube over so now it becomes the solved bottom layer (easy with a little practice).
- Solve the middle layer:
Rotate the middle so centers are correct, and then move edges between the up and middle layers until the middle is solved. If an edge first needs to be flipped, move it be FU and do the edge flipper of Step 3 (the edge gets flipped, and now rotate the top to move it back to be FU). Parentheses are just to make the sequence easier to read.edge mover, FU -> FR: (U R) (U- R-) (U- F-) (U F)- Flip the up edges so they all have the correct color on top:
If no up edges have correct top color, first do the edge flipper. Now position the cube so UL has correct top color and UF does not, and do the edge flipper once or twice.edge flipper: F (R U) (R- U-) F-- Move the up layer edges to their correct positions:
As needed, re-position the cube and do the edge swapper.edge swapper, UF<->UL: (R U) (R- U) (R U2) (R- U)- Position the up layer corners:
The corner cycle leaves UFR alone and cycles the other three counterclockwise. Identify one corner that is correct (but may be rotated), or if there is not one, do the corner cycle. Then re-position the cube so UFR is correct, and then corner cycle once or twice.corner cycle: (U R) (U- L- ) (U R-) (U- L)- Rotate the up layer corners (read this whole step before starting it):
*** Don't worry that the bottom is mixed up as you do this, it will be ok in the end.
Position the cube so UFR is not correct and repeat these two steps until all corners correct:
- Repeat the corner rotator until the UFR corner is correct:
corner rotator: R- D- R D
- Rotate the up layer (not the whole cube) so that UFR is incorrect.
Each sequence has a natural rhythm, but an easy mistake is to start off wrong. The Edge Mover and Corner Cycle start with U, the Edge Flipper (after parking the F) and the Edge Swapper start with R. To avoid forgetting your place, run the sequence in your head, and when you get faster, simply count 1,2,3,4,... as you go; 8 for the edge mover, edge swapper, and corner cycle; 4 between the F's of the edge flipper; 2 sets of 4 for the corner rotator.
Edge Mover (for Step 2):edge mover, FU -> FR: (U R) (U- R-) (U- F-) (U F)Edge Flipper (for Steps 2 and 3):
It starts with a U, and every other move involves a U or U-.
First two moves and last two moves are clockwise, middle four moves are counter clockwise.
First 4 moves involve R, second 4 moves involve F.edge flipper: F (R U) (R- U-) F-Edge Swapper (for Step 4):
"Park" the front with F, do (RU) (R-U), and then "unpark" the front with F-.edge swapper, UF<->UL: (R U) (R- U) (R U2) (R- U)Corner Cycle (for Step 5):
It's R R- R R- interleaved with U U U2 U. The R's alternate + and -, and the U's keep going clockwise, where the third is 180 degrees.corner cycle: (U R) (U- L- ) (U R-) (U- L)Corner Rotator (for Step 6):
It's U U- U U- interleaved with R L- R- L.corner rotator: R- D- R D
Always complete this sequence before doing Step 6B; it is easy to forget the final D when you see the correct color on top.
It will be done twice (eight moves to rotate once) or 4 times (16 moves to rotate twice).
Step 1: After getting faster at the other steps, this step can become the slowest. Starting at one corner and working across the top works, but at each step one is hunting for one or two specific pieces to place next, and that can be slow. A faster approach may be to pick a middle piece, say white, and start with it on top. Then repeatedly look for the first white edge you can find and place it. Then repeatedly look for the first white corner you can find and place it. Although not necessary once you get fast, it can help to keep the middle layer aligned so each time you find a piece it is easy to see where it needs to go.
Step 2: Instead of using the edge flipper, learn the symmetric sequence that moves an edge down counterclockwise from up to middle:edge cc-mover, UF -> LF: (U- L-) (U L) (U F) (U- F-)Or, use these two more complicated sequences that use only 7 moves:alternate edge mover, FU -> FR: (L F2) U F U- (F2 L-)Step 3: Before the final F-, if the right side of FR is not the top color, instead of wasting time to do F- F, repeat the (R U) (R- U-) before doing F-.
alternate edge cc-mover, UF -> LF: (R- F2) U- F- U (F2 R)
Step 4: If position of the top layer leaves only two adjacent edges to be exchanged, start with UF correct and do the first 7 edge swapper steps, which leaves UF unchanged and cycles the other three counterclockwise, or use the reverse sequence, shown below, to cycle them clockwise. For the case that UF and UB are correct and UL and UR are exchanged, cycling either way will leave just two adjacent edges to be fixed with a normal edge swapper.clockwise cycle UL, UB, UR: R (U2 R-) (U- R) (U- R-)Step 5: If no corners are correct, learn how to tell for which orientation of the cube the corner cycle will leave things so that a counterclockwise cycle will be needed. Or, if you have identified a correct corner and a clockwise cycle of the other three is needed, instead of doing the corner cycle twice (three times returns the cube to where it was), save time by reversing the sequence:reverse corner cycle: (L- U) (R U- ) (L U) (R- U-)Step 6: Every iteration of the corner rotator exchanges UFR and DFR, and repeating it 6 times returns the cube to where it was. Step 6A will use the corner rotator 2 times if the top color is on the right side of the UFR corner, or 4 times if it is on the front, in which case it is faster to do the reverse sequence 2 times (easy, start with D- instead of R- and everything follows):reverse corner rotator: D- R- D R
Step 6 is the same as Step 3 of the solution presented for Rubik's 2x2x2, and we repeat here the observations from that page:
- Step 6A affects only 4 corners by exchanging two front right corners and also exchanging the two back down corners.
- Doing Step 6A twice leaves corners in the same positions, except those four corners are rotated, and doing Step 6A six times leaves the corners the same as when you started.
- On the up layer Step 6 only modifies the front right corner.
- Since Step 6 started with the down corners correct, once three of the four up corners have been fixed, fixing the fourth up corner must leave the down layer correct. This is because when at every 6th move the two back down corners are correct, all that is left that could be incorrect are the two front right corners, but due to parity considerations, a completely solved puzzle except for two adjacent corners is not possible (however, although not hard to overcome, this is not true for the Rubik 3x3x3 Void Cube).
- The only edge pieces that are affected are FR, RD, BD, which are on the lower two layers; they return back to where they were after 6 moves.
It is interesting to see that the Corner Rotator can be used for Step 5, by memorizing two "do simple nothing" sequences:
5 (alternate). Position the up layer corners:Let S be the sequence of Step 6A, and let X be the sequence S S S- S- (which does nothing) interleaved with rotating the up layer 360 degrees with U U U2:Although this sequence is relatively long after expanding each S to the corresponding four moves, it is relatively easy to remember as the interleaving of two do-nothing sequences. In addition, if you forget what it does, a pencil and paper can be used to draw what happens to the up layer; see the explanation and diagrams presented for the Rubik's 2x2x2 Rubik 2x2x2 alternate solution.alternate corner cycle: Z = S U S U S- U2 S-Z does a counterclockwise cycle of UFR, UBR, UBL; repeat it until at least one up corner is correct (but may be rotated), re-position the cube so this corner is UFL, and then continue repeating it until all up corners are in their correct positions.
Recall the corner cycle sequence of step 5 of the six step solution):corner cycle: (U R) (U- L- ) (U R-) (U- L)A completely solved 3x3x3 cube except for two adjacent corners exchanged is not possible due to parity considerations; that is, if just two adjacent corners are interchanged, then it must be that the edges are not completely solved. This is possible for the Rubik's 2x2x2 cube, but the corner cycle sequence can still be used because there are no edge pieces to be disturbed.
It's U U- U U- interleaved with R L- R- L.
Here is a simple algorithm:Rotate the top layer to see if there is a cube that can be placed in its proper position while leaving the other three to be fixed using the corner cycle; if so, all set.It could be that UBL and UBR also have to be exchanged, in which, after fixing UFL and UFR, rotate the top 180 degrees and repeat the above sequence to exchange them.
Otherwise, rotate the top layer so that UFL and UFR need to be exchanged, and do the corner cycle sequence:

Here is a different approach that starts with solving the corners, then the top and bottom edges, and finally the middle edges.
1. Solve the corners using a solution for Rubik's 2x2x2.
2. Position up and down edges by moving to and from the middle layer:3. Use this to flip up and down edges (parentheses are just to make the sequence easier to read):
- Cycle edges between the middle and up layers to get three top edges correct:
RB -> FU, FU -> FD, FD -> RB: F M F-
That is, repeatedly position the cube so that the edge to be moved is RB, rotate the U layer so that where you want to move it to is FU, and cycle.
- Turn the cube over, and repeat Step A.
- Move the edge that goes to FD to the FU position; then move final edge to FU.
Flip the UF edge: F- M (F M)2 F-4. Use rotations of the middle layer and these to position middle edges:Front back swap, LF <-> LB, RF <-> RB: (R2 M2)25. Use this to flip middle edges (for right to left diagonal, do B2 before and after):
Clockwise cycle, RF -> LB -> RB -> RF: (R2 M) (R2 M-)
Although not necessary, these can save time:Diagonals swap, LF <-> RB, RF <-> LB: M L2 R2 M- L2 R2
Counter clockwise cycle, RF -> RB -> LB -> RF: (M- R2) (M R2)Flip RF and RB: (R M-)3 R M2 R (M- R)3
Although not necessary, this can save time:Flip RF and LB: (R M-)3 (R M) (R M-)3 (R M)
*** Don't bother with this until you are good at the standard 3-step solution; the same notation is used here.
It is interesting that the corner cycle and corner rotator operations from the standard 3-step layer by layer solution can be used for an edges first approach to solving. The sequenceS = U- R U R-rotates the three edges around the upper right by doing:UF -> UR, UR -> FR, FR -> UFIt leaves the UF and UR edges in the same flip orientation, and flips the flips the FR edge when it moves up. It has the side effect of permuting the UFL, UFR, UBR corners, but that won't matter because here we will be solving corners last.
Given S, here is an outline of an edges-first approach to solving:
1. Solve the top layer edges, and turn the cube over (easy with a little practice).
2. Solve the middle layer:Rotate the middle so centers are correct, and then use S to place each of the edges. S can be used to move an edge up to the top to then go to a different middle position. Also, if an edge needs to be flipped before placing it, rotate the up layer and position the cube so you want to move UB to RB with a flip, and do S in reverse:3. Solve the top edges:T = R- U R U-S can be used to permute edges; for example:4. Position the corners:S U- S U- does the cycle UF -> UL -> UB -> UFIf some edges need to be flipped, some clever playing around with S and T should work.First, use the corner cycle operation to get the correct corners on the top and bottom (by temporarily positioning a side face to be up), then use it on the up and down faces.5. Rotate the corners:Use the corner rotator operation to finish the up and down faces.
In time, for smoother operation, cubes were sold with redesigned central axes and adjustable springs in the centers; here is an example:







Plastic, stickerless, made in China, purchased from Amazon.com in 2015.
(left: Newisland, sold by YaMiYo, comes in a with a storage bag, 3.25" square;
right: DaYan, sold by Maxin, comes in a fitted box, 2.3" square)
In the early 2000's, smoother working versions of Rubik's 3x3x3 were widely available, with screws / springs for adjustable tension and smooth turning even when layers are not exactly aligned (beveled interior corners in conjunction with the spring action give a minimal degree of automatic alignment). The Newisland cube shown above was a gift from a friend who does speed cubing; it is smooth and quiet, comes with a storage bag and directions, and its literature explains PA plastic lower resistance, anti-popping, and internal construction. The less expensive Da Yan cube shown above has different but similar construction; here are photos of it apart:




Here are two examples of more expensive cubes advertised for speed cubing.Rubik 3x3x3 With No Center Assembly
In addition to complex mechanisms that include screws and springs, the Valk cube shown on the left below has magnets to give a slight click stop effect. The GANs cube on the right below has a similar weight and smooth action as the Valk, but with no magnets.
Both are beautiful cubes that are pleasurable to use, even if you are not speed cubing.

"Valk 3", designed by Mats Valk,
purchased from Amazon.com 2017.
(plastic, 2+3/16" square;
3.75" square box with a magnetic lid
and extra stickers and springs)
"GANS 356 Air Advanced,
purchased from Amazon.com 2018.
(plastic, 2+3/16" square;
with display box and nut tool,
and 4 pages of instructions 1, 2, 3, 4)
The original Rubik cube as well as modern versions are all based on a center spindle assembly that connects the six center squares and holds the whole cube together where the other pieces flow around it.
The Rubik 3x3x3 Void Cube is based on a completely different idea. There are no centers (one can pass their finger through the cube in all three directions).
The Rubik 3x3x3 Edges Only Cube (a.k.a. cornerless void cube) uses the same mechanism and eliminates the corner pieces as well.
One way to measure large is the dimension of the cube; for example cubes of size 33x33x33 have been made. But another measure is the physical size of the cube. This cube, made by Tony Fisher, is 1.57 meters (over 5 feet) tall:



McDonalds, 2.2"

Chex Cereal, 2.2"

Jack Daniels, 2.2"

UPS, 2.2"

Mickey Mouse, 2.2"

MatLab, 2.2"

Small Cube, 1.2"

Small Shiny Cube, 1.2"

Dice made by Volker (Germany), 2.2"
Assembly Cube, 2.2"
Beust's Page, from: http://beust.com/rubik
Bieber's Page, from: http://www.ronaldbieber.de/Fun/Rubik
Chess And Poker Page, from: http://www.chessandpoker.com/rubiks-cube-solution.html
Cheyer's Page, from: http://www.ai.sri.com/~cheyer/rubiks/rubiks.html
Dedmore's Page, from: http://www.helm.lu/cube/solutions/rubikscube
Dry Erase Board Page, from: http://www.thedryeraseboard.com
Fridrich's Page, from: http://ws2.binghamton.edu/fridrich/cube.html
Jaap's Page, from: http://www.jaapsch.net/puzzles/cube3.htm
Jasmine Page, from: http://peter.stillhq.com/jasmine/rubikscubesolution.html
Jeays' Page, from: http://jeays.net/rubiks.htm
JJuergen's Page, from: http://www.mathematische-basteleien.de
Marshall's Page, from: http://helm.lu/cube/MarshallPhilipp
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/rc/RubCub0.htm
Monroe's Page, from: http://www.alchemistmatt.com/cube/rubik.html
Nerd Paradise Page, from: http://www.nerdparadise.com/puzzles/333
Olefsky Puzzle Solver Page, from: http://www.puzzlesolver.com
Ortega and Jelinek Corners First Solution Page, from: http://rubikscube.info/ortega.php
Oxford ComLab Text Solution, from: ftp.comlab.ox.ac.uk
Petrus' Page, from: http://lar5.com/cube
Rob's Rubik Repair Page, from: http://www.roobik.com/cgi-bin/rubix/rubix.cgi
Rubiks.com Solution, from: http://www.rubiks.com
Scared Cat Page, from: http://www.scaredcat.demon.co.uk/rubikscube/the_solution.html
Shengshou Speed Cube Solution, from: http://www.speedsolving.com/wiki/index.php/Shengshou
Shon's Rubik's Place Page, from: http://www.rubiksplace.com
Still's Page, from: http://peter.stillhq.com/jasmine/rubikscubesolution.html
V-Cube Page, from: http://www.v-cubes.com/v-cube-world/v-cube-news/how-to-solve-the-v-cube-3
You Rubik Page, from: http://www.yourubik.com
WikiHow Page, from: http://www.wikihow.com/Solve-a-Rubik's-Cube-(Easy-Move-Notation)
Rubik Hungarian Patent, BE887875.
Rubik U.S. Patent, from: www.uspto.gov - patent no. 4,378,116
Sugden Patent, from: www.uspto.gov - patent no. 6,974,130
Sugden Design Patent, from: www.uspto.gov - patent no. D495,378
Scott Patent Application, from: www.uspto.gov - application no. 2010/0230897
God's Number is 20, from: http://www.cube20.org
Kociemba's Two Phase Algorithm and Cube Math, from: http://kociemba.org/cube.htm
22 Moves, from: http://www.springerlink.com/content/q088143tn805k124/fulltext.pdf
Speed Solving Page, from: http://www.speedsolving.com/wiki/index.php/Main_Page
Superflip, from: http://www.speedsolving.com/wiki/index.php/Superflip
Rubiks.com Page, from: http://www.rubiks.com
Rubiks.com Booklet, from: http://www.rubiks.com
Rubiks.com Diagrams, from: http://www.rubiks.com
Rubiks Cube Typesetting with TeX, from: http://www.ctan.org/pkg/rubik
Rubik's Home Cube Assembly Instructions, from: http://www.rubiks.com/World/Rubiks%20downloads.aspx
Philip K's Rubik's History Puzzle List, from: http://hjem.get2net.dk/philip-k/puzzles/puzzlist.htm
Cube Lovers Archive, from: http://www.math.rwth-aachen.de/~Martin.Schoenert/Cube-Lovers
Wikipedia Page, from: http://en.wikipedia.org/wiki/Rubik%27s_cube
Wikipedia - God's Algorithm, from: http://en.wikipedia.org/wiki/God%27s_algorithm
Wikipedia - solutions, from: http://en.wikipedia.org/wiki/Optimal_solutions_for_Rubik's_Cube

Made by SOCUBE, Kuala Lumpur, Malaysia, 2009.
(plastic, 2.1 x 2.1 x 1 inch;
white opposite yellow, red opposite orange, blue opposite green)

Availabe at McDonalds in the U.K. 2002.
(plastic, 3.5 inches)
A very easy (but cute) puzzle.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/morph.htm




TM & Copyright Universal Studios, sold with McDonalds Happy Meals, 2018.
(plastic, 1 x 2 x 3 inches)
A simpler puzzle in the theme of Rubik 1x3x3. Part of a collection of 1x2x3 and 2x2x2 Rubik's cubes sold by McDonalds. Has the Minions characters from the 2010 movie Despicable Me. These versions are identical except that the one on top has its first row with arched edges. On the bottom left of the one on top it says:Further Reading
Minions Wikipedia page, from: https://en.wikipedia.org/wiki/Minions_(Despicable_Me)
Purchased 2012.



(plastic, 3.9" x 1.5" x 3/4" inches)
A mechanically fun and not too hard puzzle, although the graphics can make it confusing to look at it mixed up and determine what needs to be done. Jaap's Page presents a solution that first solves the edges and then the corners.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/index.htm


Rubik 1x2x9 "Chopsticks",
designed by Oskar Van Deventer and Ola Jansson, sold by Mefferts 2013.
(plastic, 5+1/8" x 1+7/8" x 1+3/8")
A longer puzzle in the theme of Rubik 1x2x5. Shown above is the puzzle and it turned over.

a.k.a. Unlucky Twist
Designed and custom made by Oskar Van Deventer, 2013.
(plastic, made with a 3D printer, 10.25" x 1.5" x 3/4")
A larger version of the mass produced Rubik 1x2x9. Here are photos of successive manipulations, where the third photo is a close up of the center of the second one to see how the mechanics of how the layers build out from the middle cube:






Designed by Katsuhiko Okamoto 2007, purchased from Gentosha, Japan, 2009.
(plastic, 2.25 by 2.25 by 3/4 inches;
by the same designer as the Rubik 3x3x3 Void Cube)
Seems to impossibly stay together as sets of three are flipped:



Notation: L (left), R (right), F (front), B (back) denote flip that side.
Jaap's Page presents a computer analysis that shows there are only 192 reachable positions, each requiring at most 8 moves to solve. By just playing with this puzzle it usually does not take very long to solve, or to get it to where it can be fixed with the following simple transformation:

F R F R F R
(flip two adjacent edges)
The directions that came with the puzzle also present the following transformations (after doing the last two, rotate or turn the puzzle over to get the views shown):
Further Reading

L F L R B R
(flip two opposite edges)
L F L R F R
(exchange opposite edges)
F L R B
(flip center and
exchange two opposite edges)
Jaap's Page, from: http://www.jaapsch.net/puzzles/floppy.htm

a.k.a. Magic Floppy Cube
Made in Hong Kong, 2009.
(plastic, 2.25 by 2.25 by 3/4 inches)
A version of the Rubik 1x3x3 Floppy Cube where the cube sizes progress from small to large in both horizontal dimensions; it can be solved in exactly the same way. Fun shapes can be formed:




Unlike the Rubik 3x3x3 Mirror Cube which progresses in all three dimensions, here all cubes have the same thickness and not all unsolved positions have a jumbled shape. In fact, because for this puzzle it is very easy to get back to the square shape, it is perhaps even easier to solve than the normal floppy cube. By randomly mixing and restoring to a square the puzzle is typically quickly solved or in a position where two adjacent edges are flipped, which can easily be fixed with the following transformation (F and R denote flips of the front and right sides, 3 means do it three times):

(F R)3


Designed by Katsuhiko Okamoto, made by Gentosha, Japan, 2010.
(plastic, 2.25 by 2.25 by 3/4 inches)
A generalization of the Rubik 1x3x3 Floppy Cube Rubik 1x3x3 Floppy Cube where a 1x1x2 portion can rotate (see also the Rubik 1x3x3 Floppy Mirror Cube); here are a sequence of three moves to make an edge piece sit up:



Jaap's Page presents an analysis, but by just playing it is relative easy to solve, and it is easy to make interesting shapes, like the one on the left below, and then return the puzzle to flat.


Notation: L (left), R (right), F (front), B (back) denote flip that side, L90 to turn the left side 90 degrees clockwise, B90 to turn the back side 90 degrees clockwise.
Once flat, moves for the 1x3x3 Floppy Cube can be used to solve or to be left with one edge flipped as shown on the right above. To fix this, make the edge opposite to this edge sit up, then use the edge pair flipping transformation from the 1x3x3 Floppy Cube (LFL RBR), and then put the opposite edge back down; all 90 rotations are in pairs, so all movement can be clockwise:L90 B90 L90 L F L R B R L90 B90 L90
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/floppy2.htm

Made by J. A. Storer from a standard Rubik 2x2x2 cube, 2007.
(two brass plates glued to a Meffert's Eastsheen Rubik 2x2x2 cube, 2 inches)
This is a relatively easy puzzle that can usually be solved without too much effort by playing a bit. However, it can get more mixed up than is first apparent. An organized way of solving is to combine repositioning of the bandaged portion with transformations for the standard Rubik's 2x2x2 cube that only use R and D rotations, such as these which are shown on Jaap's Page.
Notation: R (right) and D (down) for 90 degree clockwise rotations of the corresponding faces, - to do counterclockwise instead of clockwise, and 2 to do it twice; corners are denoted with three letters (e.g., FLD- = counterclockwise rotation of the front, left, down corner).FLD-, BRD+: R2 D- R D2 R- D2 R D- R2 D
FRD-, BRD-, BLD-: R- D- R D- R- D2 R D2
FRD+, BRD+, BLD+: D2 R- D2 R D R- D R
FRD-, BRD+, BLD-, FLD+: R2 D2 R D2 R2 D
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/cube2.htm

Made by J. A. Storer from a standard Rubik 2x2x2 cube, 2007.
(four brass plates glued to a Meffert's Eastsheen Rubik 2x2x2 cube, 2 inches)
This is an easy puzzle, but still fun, that can be solved without too much effort by playing a bit.

a.k.a. Rubik 2x2x2 Super Square
Made in China, 2010.
(plastic, 2.2 inches)
Works like a Rubik 2x2x2, and also each face has a circle that rotates. So this puzzle is a bit like a 2x2x2 nested inside a standard 2x2x2 cube.



Two, three, or four Rubik's 2x2x2 cubes joined, purchased from UK3 2005.
(plastic, each formed from 7/8 inch 2x2x2 cubes inches)




Made for McDonalds 2018, copyright Rubiks 1974.
(plastic, 2+1/8" square)
Further Reading Minions Wikipedia page, from: https://en.wikipedia.org/wiki/Minions_(Despicable_Me)


a.k.a. Slim Tower, Franken Tower
Made by Gentosha, Japan, 2009.
(plastic, 1.5 x 1.5 x 2.25 inches;
generic (left): opposite red is orange, opposite blue is green, opposite yellow is white;
Gentosha (right): opposite red is yellow, opposite blue is light green, opposite gray is black)
An extended Rubik's 2x2x2 where two dimensions are restricted to 180 degree rotations.
Notation: With a 2 high by 3 wide surface facing you, F (front), B (back), U (up), and D (down) denote 180 degree clockwise rotations of the corresponding faces, L (left) and R (right) denote a 90 degree clockwise rotation of the corresponding faces, - to rotate counterclockwise instead of clockwise, 2 or 3 to do it two or three times.
Solution: The solution that comes with the Gentosha puzzle gives the following transformations that may be used to solve the corners and edges independently.It's easy to make the left and right faces their correct color but with some or all of the corners out of place; then solve the corners using the following transformation as needed:BRU <-> BRD: U F R F L- U L U R- U RSolve the edges using the following transformation as needed:UF <-> UB: (U R2)3
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/cube223.htm


Made in Japan, purchased from Mefferts 2010.
(plastic, 1.7" x 1.7" x 3.4"
green opposite yellow, red opposite orange, white opposite blue)
Unlike Rubik 2x2x3, 90 degree turns on the long dimension can lead to jumbled shapes; here is a sequence of three 90 degree turns:



Solution
1. Return the puzzle to the correct shape.One approach is to think of this as a 2x2x2 cube formed by the center portion with stuff hanging off of it, and employ Rubik 2x2x2 transformations.2. Use a solution for Rubik 3x3x4.(Steps to correct edge pieces can be omitted).

a.k.a. Rubik 2x2x4 Super Square
Made in China, 2010.
(plastic, 2.2 inches)
The middle portion is just like a Rubik 2x2x2 Nested, (where each face has a circle that rotates), and then this puzzle has a standard layer added to the top and bottom.






a.k.a. Overlap Cube
Designed by Oskar Van Deventer, purchased from Shapeways 2013.
(Lots of little uncolored plastic pieces in a 3.5" by 5.5" plastic bag;
buyer must color and assemble to have a puzzle as shown in the pictures above
from the Shapeways web page; good luck!)


Designed by Erno Rubik 1983; left purchased circa 1985; right purchased 2009.
(plastic, 1.5 inches high by 2.25 inches square)
Put the numbers in order on both sides.
Notation: R for a flip of the right side, U, D for clockwise rotations of the up and down faces (- for counterclockwise, and 2 to do it twice). We also use M to denote rotating the whole puzzle 90 degrees clockwise (with respect to looking down), as a convenience so that only right flips are needed (easier to hold and also useful for the solution to Rubik 3x3x4).
Move pieces to their correct layers:
1. Repeatedly position pairs of edges on the wrong layers on the right and do R.
2. Repeatedly position two corners on the wrong layers at the front right and do:Exchange UFR and DFR: R U R U- RSolve the two layers independently:
3. Use this to permute corners; X = Step 2 transformation, Y = reverse of X:Exchange URF and URB: X M- Y D-4. Use this to permute edges:Exchange UF and UR: (R U)2 (R U2)2 XJaap's Page presents the transformations above (and others), as well as the following transformation to change a side to its mirror image (F denotes a front flip):Further reading:
R F T- F T2 R (T F)2 T2 R T- F R
Jaap's Page, from: http://www.jaapsch.net/puzzles/domino.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/rdml/rubdom1.htm

Made in China, purchased 2010.
(plastic, 1.5 inches high by 2.5 inches diameter)
A smaller version of Rubik3x3x3 Layered and mechanically the same as Rubik2x3x3, but with each layer being a single color (and this version has been made in a circular shape).
Although any solution for Rubik's 2x3x3 could be used, the puzzle is much easier to solve. It is easy to flip the sides as needed to make the centers match the edges (i.e., each side has a cross of a single color). Then corners can be fixed with just 180 degree rotations of the front (F2) and clockwise or counter-clockwise rotations of the top (U, U-). If you want to memorize a simple transformation, this one exchanges the front top left corner with the front bottom left corner:F2 U F2 U- F2After the above transformation has been used to fix pairs of corners, such shown below on the left, a flip of the front and back sides followed by a flip of the left and right sides gives the checkerboard pattern shown below on the right.




Made in China, 2012.
(plastic, 2.8" x 2.1" x 1.4" inches)
The shape can change quickly. Here are three successive moves; the first turns the back face 90 degrees clockwise, the second turns left and right two halves 180 degrees with respect to each other, and the third turns the front face 90 degrees counter clockwise:



Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/cube234.htm


a.k.a. WitEden 2x4x4
Purchased from Mefferts, 2013.
(plastic, 2.7" x 2.7" x 1.75";
white opposite yellow, green opposite bule, orange opposite red)
The top and bottom layers can rotate 90 degrees; the other rotations are limited to 180 degrees.


Copyright Winning Moves Inc. 2020.
(plastic 2.25 inches square, white opposite yellow, green opposite blue, orange opposite red)
A version of the standard Rubik's 3x3x3 cube, and although any solution for the standard Rubik's 3x3x3 Cube can be used, the jumbled shape it takes when mixed up can make it much harder to perform a solution. For an even harder version of this puzzle to visualize while solving, see the Rubik's Mirror cube that has all faces the same color.
Here are photos of the other sides of the puzzle, the puzzle shape as shipped, and starting with a clean 3x3x3 cube, what it looks like after just the three moves R F R-:




a.k.a. Yong Jun Cube
Purchased from Yong Jun Toys / Mega House, 2009.
(plastic with silver stickers, 2.25 inches)
A version of the standard Rubik's 3x3x3 cube where the cube sizes progress from small to large in all three dimensions. Each piece is distinguished by its shape rather than it color. Here are photos of three successive moves:



Any solution for the standard Rubik's 3x3x3 Cube can be used, although it may be more confusing to identify each piece based on its shape when the puzzle is mixed up than it is to look at colors on a standard cube. Rubik's Color Blocks is arguably a more friendly version of this puzzle that has colored sides.

a.k.a. Square King
Designed by T. Fisher, purchased from Mefferts 2009.
(plastic, 2.2 inches;
silver opposite gold, green opposite blue, red opposite orange;
also made with a black body)
Works just like a a standard Rubik's 3x3x3 Cube, but can be confusing when the shape becomes very jumbled. Meffert's also made this puzzle in all silver and all gold, and versions from China were sold as the "Square King":



Here are photos of 4 consecutive moves:








a.k.a. Holey Cube
Designed by Katsuhiko Okamoto 2007,
top by Gentousha 2009 and uses stickers,
bottom two purchased from CubeFans 2009 and are all plastic.
(plastic, 2.25 inches;
top: gray opposite black, red opposite yellow, blue opposite light green;
bottom: green opposite blue, yellow opposite white, red opposite orange)
By the designer of the Rubik 1x3x3 Floppy Cube. Logically the same as the classic Rubik's 3x3x3 Cube, but mechanically very different. The standard Rubik's 3x3x3 cube relies on central 3D axes to which the centers are attached and the other pieces flow around. Here, one can look through the center of the cube along any of the three axes (i.e., a square bar with a 1x1 unit cross section can be passed through the cube in any of the three directions). Solving is the same as the standard version, except for the void cube parity issue, described on the following page.
In a standard Rubik's 3x3x3 Cube, not all possible positions are reachable by mixing up the puzzle. For example, it is not possible to end up with the cube solved, except for two adjacent corners exchanged. Note that this fact is not at odds with such a situation being possible for the Rubik's 2x2x2 Cube, which has no middle layers. For example, cycling the UFL, UBL, UBR corners counterclockwise followed by rotating the up layer 90 degrees clockwise results in the UFL and UBL corners being exchanged and the remainder of the 2x2x2 cube unchanged, but for the 3x3x3 cube this would leave the edges of the up layer disturbed.
The void cube parity problem is when the puzzle is almost solved in an apparently impossible position. For example, using the simple layer at a time solution, as was presented for the standard Rubik's 3x3x3 cube, you may get stuck at the end with something like this:

Such a configuration corresponds to a standard Rubik's 3x3xx3 cube where in addition to the two exchanged corners, some center squares are mixed up as well. Other solution approaches could result in impossible configurations of the edges. With the void cube, there are no middle tiles to get mixed up, and some impossible positions for the standard 3x3x3 cube are now possible.
Rather that mix up up the puzzle and try again, there are many ways that have been published for fixing the problem. But without having to remember something new, a simple approach is to try to solve using whatever method you use for the standard cube, and if it works fine (you lucked out and got the right mode of parity), and if not, go back to a place where you can make a move that will change parity with respect to the center squares and resolve from that point forward.
When using the basic 6-step layer by layer solution for Rubik's 3x3x3, one can just solve as usual, hoping things will work, and if not, rotate the middle layer 90 degrees, and then resolve from that point on.
When using a corners first solution, at the last phase that solves the middle, the same sequences can be used, possibly preceded with an additional 90 degree rotation of the middle layer.


a.k.a. Cornerless Void Cub
Left: made by Smaz Smart Toy Shop IQ Toys from a Gentosha Void Cube 2009.
right: mass produced by Cube For You (C4Y) 2009;
(plastic, 2.25 inches,
left: white opposite yellow, blue opposite green, orange opposite red,
right: blue opposite green, purple opposite red, and yellow opposite gray;
left looks nice, right has a smoother mechanism)
A simplified Void Cube that removes everything but the edges from a standard Rubik 3x3x3 Cube; complements the Rubik 2x2x2 Cube that removes everything but the corners.




The puzzle has exactly two solutions. To see this, observe that for each color there is exactly one other color for which it shares no edge, so this determines the pairs of colors that are opposite each other. Now choose two adjacent colors to make a standard orientation with one on the top and one on the front (for example, for the puzzle on the left above, blue on top and purple on front), which uniquely determines the bottom and back colors, and now it is possible to solve the puzzle with either choice for the left and right colors.
Although a solution for the void cube can be used here (omitting solving corners), shorter sequences can be employed because there is no need to avoid disturbing the corners when manipulating the edges.

Rubik 3x3x3 with graphics on the middle squares, produced in 1988.
(plastic, 2.1 inches)
Many promotional versions of the standard Rubik's 3x3x3 cube have graphics printed on the faces that require the middle square to be properly oriented. Rubik's 3x3x3 Fourth dimension adds minimal graphics for this purpose. Here are the directions from from the box lid:

Some Rubik's solutions, such as Marshall's Page, employ transformations that preserve center orientations. For others the centers can be fixed at the end with simple moving around and rotating of the middles that does not affect the remainder of the puzzle. The Dry Erase Board Page gives the following idea:0. Optional: Rotate an outside layer (or more than one if you want).Jaap's Page gives specific transformations.
1. Rotate a middle layer.
2. Rotate a different middle layer.
3. Reverse step 1.
4. Reverse step 2.
5. Reverse step 0.
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/cube3.htm
Dry Erase Board Page, from: http://www.thedryeraseboard.com/mechpuz/333/centersolve
Marshall's Page, from: http://helm.lu/cube/MarshallPhilipp/Rubikfourth.htm

Sold in Scotland, 2019.
(plastic, 1+3/8 inches square)
Like the Rubik 3x3x3 Fourth Dimension orientation of center squares matters. In addition, all sides are different but similar (harder to see where squares should go when the puzzle is mixed) and the centers must be oriented to match the direction of the fabric:

top
front
botttom
back
left
right

Custom made Rubik's 3x3x3, one color per layer, purchased 2006.
(plastic, 2.2 inches)
Mechanically the same as Rubik's 3x3x3, but with each layer being a single color. Although any solution for Rubik's 3x3x3 could be used, the puzzle is much easier to solve; the solution below is the same as that for the Rhombi Diamond.
Solution:
1. Solve the middle layer.Easy if you don't care about the rest of the puzzle.2. Solve the top and bottom edges.Easy by using 180 degree front rotations to exchange incorrect edges.3. Solve the bottom back right and bottom back left corners.It is easy to play with top rotations and 180 degree front rotations to make at least one bottom corner red; rotate this corner to the bottom back right. If the bottom back left corner is green, play some more with these rotations to make the top front left and top front middle red, then rotate the front 180 degrees to bring these two red cubes down, and then rotate the bottom 90 degrees to bring the red corner to the back right (and making the red corner that was in the back right now in the back left).4. Solve the remaining incorrect corners.This can be done with just 180 degree rotations of the front (F2) and clockwise or counter-clockwise rotations of the top (U, U-). If you want to memorize a simple transformation, this one exchanges the front top left corner with the front bottom left corner:F2 U F2 U- F2


Ideal Toy Co., 1981.
(plastic 2.2 inches, with cardboard can with plastic lid)
A standard Rubik's 3x3x3 Cube for which each day of the year one can solve the top face to that day. It is much easier than the standard cube, since only one side has to be solved. For a given day, the top left and bottom right corners of the top face are blank, the top middle square has day, the top left has one of Sun, Mon, Tues, Wednes, Thurs, Fri, Satur, the middle three squares are the month, JAN, FEB, MAR, APR, MAY, JUN, JUL, SEP, NOV, DEC, and the bottom right two squares are the date (or just the bottom right if the date is only one digit).
Here is a Dutch version Here is a Dutch version solved for Monday, Jan 1 on the left, and on the right the other three sides for this solution (in Dutch, day=dag, Sunday through Saturday are Zondag, Maandag, Dinsdag, Woensdag, Donderdag, Vrijdag, Zaterdag, and January through December are Januari, Februari, Maart, April, Mei, Juni, Juli, Augustus, September, Oktober, November, December).




a.k.a. Bicube
Made by Mefferts, 2009.
(left: plastic 2.3 inches, red opposite white, yellow opposite orange, blue opposite green;
right: plastic 1+5/8", red opposite orange, green opposite blue, yellow opposite white)
The bandages restrict the way in which a Rubik's 3x3x3 cube can be mixed up, and the sequences to solve it are also restricted. Jaap's Page presents analysis and solution sequences. Here is what the other three sides look like:


Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/bandage.htm


a.k.a. Fused Cube
Made in China 2008.
(plastice, 2.2 inches)
In a theme similar to Rubik's 3x3x3 Bandaged, the "patches" restrict the way in which a Rubik's 3x3x3 cube can be mixed up, and the sequences to solve it are also restricted. Here is what the other three sides look like:



a.k.a. Brick Cube
Made by Hidetoshi Takeji, 2008.
(plastic, 2.2 inches)
This is a Rubik's 3x3x3 cube that has been patched in pairs along two of the three dimensions; to see this, rotate the middle section by 90 degrees:

Here is what the other three sides look like:



Designed by Katsuhiko Okamoto, purchased in Japan, 2010.
(plastic, 2.2 inches square)
Like a standard Rubik 3x3x3 cube but movement is restricted so that a face may only turn in the direction of the arrows. When solved, all faces have consistent arrows and can rotate only in the indicated direction. When mixed up, some faces may have no arrows (and can rotate in either direction) and some faces may have arrows in both directions (and cannot be rotated in either direction). Here are box back and the other three sides:


a.k.a. TomZ Constrained Cube, Tom's Constrained Cube
Purchased from Mefferts, 2012.
(plastic 2.2" square;
TomZ Constrained Cube 90,
TomZ Constrained Cube 180,
TomZ Constrained Cube 270,
TomZ Constrained Cube Ultimate)
Locks in the center allow the corresponding face to only rotate a particular number of degrees. Below is a photo of the 180 degree cube, and also a photo of a second 180 degree cube which came with its blue face set to 90 degrees. The ultimate cube has a mixture of degrees on its faces, including 0 degrees.


Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/quarter.htm

Purchased from Mefferts 2018.
(plastic, 2.3" square)
Works like a standard Rubik 3x3x3 cube, and when solved, the top layer can be snapped off to access an internal compartment. Here is a view of the other three sides and the puzzle apart:




Made by Cube 4 You (C4U), 2009.
(plastic, 2.2 by 2.2 by 3 inches; white body has opposite sides white / blue, red / orange, green / yellow, the same as the color scheme as the standard Rubik's 3x3x3; black body has opposite sides black / white, red / yellow, green / blue)
This extension of the standard Rubik 3x3x3 cube allows only 180 degree rotations in two of the dimensions. One solution approach is to think of an "outer" Rubik 2x2x3 Domino formed by the top and bottom layers with an "inner" domino in the middle:
1. Solve the outer domino.
2. Solve the inner domino, except if your solution makes use of flips of the front, back, or left sides, replace each such flip by a flip of the right side (that is, rotate the middle layers appropriately, flip the right side, rotate the middle layers back).
3. If Step 2 ended up using an even number of flips, then the puzzle is solved. Otherwise, perform the following transformation, adapted from Jaap's Page for the domino, that does nothing to the middle two layers (by exchanging an upper and lower middle edge) using an odd number of flips:D2 R M- (D2 R) 3 M R D2Further Reading
Notation: R denotes a flip of the right face, M a 90 degree clockwise rotation of the middle two layers (with respect to looking down from the top), D and D- clockwise and counter clockwise rotations of the lower middle layer (with respect to looking up from the bottom), 2 and 3 mean do it two or three times.
Jaap's Page, from: http://www.jaapsch.net/puzzles/cube334.htm(Presents a similar approach with many additional transformations.)


Designed by Aleh & Eveniy, purchased from Mefferts 2013.
(plastic 3.75" x 2.25" x 2.25";
red across from orange, blue across from green, yellow across from white)

Designed by Aleh, Tont, & Eveniy, purchased from Mefferts 2013.
(plastic 3.75" x 2.25" x 2.25";
red across from orange, blue across from green, yellow across from white)
One of a number of generalizations sold of Rubik 3x3x5. Unlike the standard 3x3x5 shape or the big brother of this puzzle, the Rubik 3x3x5 Cross, the shape of the puzzle can change quickly; below are three successive 90 degree clockwise rotations:




Designed by Aleh, Tont, & Eveniy, purchased from Mefferts 2013.
(plastic 3.75"; red across from orange, blue across from green, yellow across from white)
One of a number of generalizations sold of Rubik 3x3x5. Like the standard 3x3x5 shape and the little brother of this puzzle, Rubik 3x3x5 X, the shape of the puzzle does not change as it is manipulated.

Made by WitEden, sold by Mefferts 2011.
(plastic, 2.25 inches;
WitEden made a number of variations, many sold by Mefferts,
including smaller heights, white bodies, RoadBlock versions, and Crazy versions)
Here are three successive moves (top, right, middle):




Made by WitEden, sold by Mefferts 2011.
(plastic, 2.25 inches;
a generalization of the standard 3x3x9 version; also sold in a white body)
Here are three successive moves (back two, middle slice, back):





Made by mf8, sold by Mefferts 2012.
(plastic, 2.1" x 2.75" x 3.5", with storage bag 7.4" x 5.75";
white opposite yellow, red opposite orange, green opposite blue)
For all three dimensions, only 180 degree turns are useful.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/cube345.htm
a.k.a. Rubik's Master Cube
Determine your cube color scheme: Since a Rubik 4x4x4 cube has no center squares, the first thing is to determine the color scheme of your cube (by looking at the corners and reasoning it out). Here is a diagram of the standard color scheme, which we use here:
Notation: We use the same notation as for Rubik's 3x3x3 with the additional convention that a lower case letter means move the corresponding row that is one in from that edge. For example, U, as with Rubik 3x3x3, means rotate the top clockwise 90 degrees, and u means rotate the layer below the top (the third layer up from the bottom) by 90 degrees clockwise. We use brackets to move two rows together; for example, [Uu] denotes rotating the top half of the cube 90 degrees clockwise. In fact, if it is a dexterity challenge to move a single middle layer, an easy way to do a u move, for example, might be [Uu] followed by U-.
Basic Approach:
The following three pages described the three phases of solving: Phase 1: Match up the centers.
Phase 2: Match up the edges.After Phases 1 and 2 are completed, each face will have the correct color in the center four squares and, although the edges are in general completely mixed up, they are all in matching pairs; that is a typical face, such as the red face, might look like this:Phase 3: Solve like a Rubik's 3x3 cube.
 Normal Rubik 3x3x3 moves never mess up the center groups or edge pairs (the pairs move around just like single edges do on a Rubik 3x3x3 cube). Solve using any layer at a time Rubik's 3x3x3 solution.
Normal Rubik 3x3x3 moves never mess up the center groups or edge pairs (the pairs move around just like single edges do on a Rubik 3x3x3 cube). Solve using any layer at a time Rubik's 3x3x3 solution.
It may be that after solving, there remains a single edge pair flipped and / or exactly two corners or edge pairs exchanged (which cannot happen with a standard Rubik 3x3x3 cube), and a little additional work is done to finish up.
This can be done one face at a time (in any order) with a variation on a simple 3 move sequence. For example, if there are a pair of red squares on the front face and also a pair on the up face, then the faces can be oriented so that the pairs line up, and then do:Or suppose that the front face already has three red squares and the fourth one is on the top face: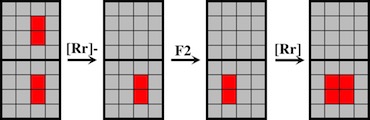 Or suppose there is a red square on the back that needs to come to the front.
Or suppose there is a red square on the back that needs to come to the front.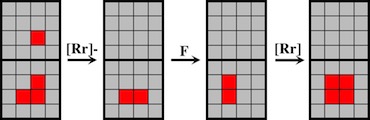 All three of these examples are essentially the same simple idea:
All three of these examples are essentially the same simple idea: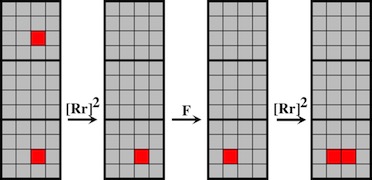 Orient the cube so that the face is on front and what you want to move to the front is on the up face or the back face, then rotate the two faces so that that after the first step you will not have two squares diagonally opposite, and do:1. Rotate the right half of the cube as appropriate (or left half also works).
Orient the cube so that the face is on front and what you want to move to the front is on the up face or the back face, then rotate the two faces so that that after the first step you will not have two squares diagonally opposite, and do:1. Rotate the right half of the cube as appropriate (or left half also works).
2. Rotate the front as appropriate.
3. Rotate the left or right half back.
Edges can be paired one at a time (in any order) by first placing two to be paired in either of the two positions shown here
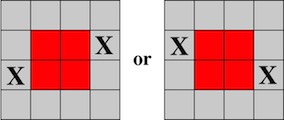
then doing [Dd] if they are positioned as on the left or [Uu] if they are positioned as on the right, then doing the simple three move sequence
R U R-
and finally doing a [Dd]- or [Uu]- to restore things. The net effect is to move XX to the up-front position, and to split the pair in either the up-back position or the up-right position. So before doing this put an unmatched pair in the up-back position if it is the case on the left above or the up-right position if it is the case on the right.
At first things are slow when one repeatedly hunts for a pair of matching squares to move them into position. If when you get them in position they are not offset, it is easy to fix that; e.g.:
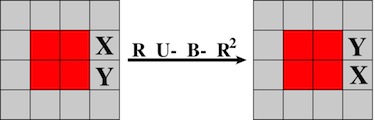
R U- B- R2
It is not necessary to memorize this sequence; regular 3x3x3 moves never un-pair edges, and just playing around suffices to move squares around. However, it saves time to remember it.
Finally, all edges will be paired, or exactly two are not, which can be paired with this sequence:
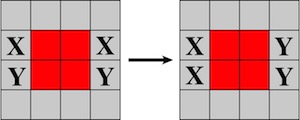
[Dd] R F- U R- F [Dd]-
This sequence is pretty easy to remember because of its symmetry, the [Dd] and [Dd]- at each end with a U in the middle, and it is RF- to the left of the U with the same to the right of the U except signs flipped to be R-F.
Step 3A: Solve using any layer at a time Rubik's 3x3x3 solution.*** At this point if you are lucky, the cube is completely solved!Step 3B: Fix OLL parity if present.
However, there is a 50-50 chance of each of two problems:PLL parity: Exactly two corners or two edges are exchanged in and otherwise solved cube.
OLL parity: A single edge is flipped in an otherwise solved cube.A complex sequence shown on the following page can be employed. However, at the cost of a little resolving, OLL parity can be fixed as follows with having to memorize anything new:Step 3C: Fix PLL parity if present.A. Do a single r move.Note: It doesn't matter how you hold the cube when you do Step A; the flipped edge can be in the front up position or any other position. Re-solving is much less work; the left and right faces are not affected, and the front top, back, and bottom faces all have the simple pattern of 2 of the correct color and 2 of the color from the adjacent face. For example, fix the front face by doing an F2 followed by the standard [Rr]- F2 [Rr] sequence of Phase 1, and repeat for the top and back face (which also fixes the bottom face). Now just a few edges need to be paired up again using Phase 2.
B. Use Phases 1 and 2 to fix the affected centers and edge pairs.
C. Solve as for Rubik 3x3Starting with the cube fully solved except for two exchanged edges or two exchanged corners on the up layer, this sequence will fix PLL parity leaving the bottom three layers still solved, and so all that is left is to re-solve the up layer (in fact, if it is a front back edges exchange, the up layer will also end up fully solved):r2 U2 r2 [Uu]2 r2 u2This sequence is relatively easy to remember as three r2 moves, each followed by a variation of an up two move; think of the up moves as going inward, first U2 (the outer face), then [Uu]2 (the outer face and inner slice), and lastly u2 (just the inner slice).
OLL Parity is the number of slice moves, a 90 degree turn of a single inner layer. For example both r and [Rr] perform a slice move, but [lr] does not be becasue it comprises two slice moves, l and r. It is when OLL parity is odd that we end up with a single edge flipped, something that would be impossible for a 3x3x3 cube. Here "fixing" OLL parity refers to reversing OLL parity from odd to even in order for the cube to be fully solvable.
The basic [Rr]- F2 [Rr] sequence of Phase 1 and the basic [Dd] R U R- [Dd]- or [Uu] R U R- [Uu]- sequences of Phase 2 do slice moves in pairs ([Dd], [Dd]- or [Uu], [Uu]-), and so Phase 1 and Phase 2 (done in the normal way) do not change OLL parity. So after Step 3B begins with a single slice move to change OLL parity, OLL parity is not further changed. And Step 3C does not change it either since it performs an even number of slice moves. So in Step 3B, after the single r move is done, it doesn't matter exactly how the cube is repaired so long as all slice mores are done in pairs (which is true of the straightforward implementations of Phases 1 and 2). Just don't try to get fancy and slip in an extra slice move.
It could be that Step 3B changes PLL parity. That's ok; Step 3C will fix it if needed.
Step 3B avoided having to memorize anything new to fix OLL parity. But if you like memorizing long sequences, this is a faster way to do it. Start with the cube solved as much as possible with the single flipped edge in the front up position, and use this sequence to correct that flipped edge and leave the rest of the cube unchanged (i.e., fully solved unless there is still an OLL parity problem to be fixed). Commas and the extra spacing have no meaning other than to help reading.r2 B2, U2, l, U2 r- U2 r U2, F2 r F2, l-, B2 r2To make it easier to manipulate the cube, r and l can be replaced by [Rr] and [Ll]. The resulting sequence shown below also fixes OLL parity, but requires re-solving the up layer. This resolving does not amount to additional work if you identify the OLL parity problem before solving the up layer (it is present if the number of the up edge pairs correctly flipped is 1 or 3).[Rr]2 B2, U2 [Ll], U2 [Rr]- U2 [Rr] U2, F2 [Rr] F2, [Ll]-, B2 [Rr]2
The terms PLL and OLL parity are standard in the Rubik's cubing literature. Parity is just a property of a current cube state that is even or odd. OLL parity is the number of 90 turns of an inner layer (a slice move r, l, f, b, u, or d), where at the end an even number is good and an odd number results in a flipped edge. PLL parity refers to a relationship between edge and corner permutations; problems can arise with even dimenson cubes where there is no center square to guide you (see also, for example, the Rubik 3x3x3 Void Cube or using a Rubik 3x3x3 solution to solve a Rubik 2x2x2 cube). Here the references to "fixing" OLL and PLL parity are just informal ways of saying that the corresponding parity needs to be reversed from odd to even in order for the cube to be solvable.
Although these parities always remain even when solving a standard Rubik 3x3x3 cube, they can become odd during the solving of a 4x4x4 cube because there is more than one visually equivalent way to configure identical pieces when forming center groups or edge pairs. For example, the figure below shows how the cube could be fully solved except for exactly two edge pairs that are exchanged (an example of a PLL parity problem). This is impossible for a standard Rubik's 3x3x3 cube but in the 4x4x4 cube, each of the two halves of two edge pairs can be exchanged independently.The complex sequences presented on the preceding page for directly solving OLL parity are from Hardwick's Page. There is much written in general about solving Rubik's 4x4x4 (and larger cubes) by reduction to 3x3x3 solving. There are also completely different approaches (e.g., layer by layer).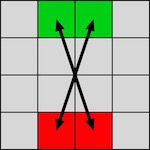
Jaap's Page, from: http://www.jaapsch.net/puzzles/cube4.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/rr/RubRev1.htm
Helm's Page, from: http://www.helm.lu/cube/solutions/revenge
Hardwick's Page, from: http://www.speedcubing.com/chris/4-movelist3.html
Hardwick's Speed Page, from: http://www.speedcubing.com/chris/4speedsolve.html
Jeays Page, from: http://jeays.net/rr.htm
Rubiks.com booklet, from: http://www.rubiks.com/World/Rubiks%20downloads.aspx
Rubiks.com assembly page, from: http://www.rubiks.com/World/Rubiks%20downloads.aspx
Adventures In Cubing Page, from: http://adventuresincubing.com/2013/08/25/4x4-parity
Rubik's Place 4x4x4 Solution, from: http://www.rubiksplace.com/cubes/4x4
Cube Skills Rubik 4x4x4 Solution, from:
http://cubeskills.com/uploads/pdf/tutorials/beginners-method-for-solving-the-4x4-cube.pdf
Ruwix Notation, from: http://ruwix.com/the-rubiks-cube/notation/advanced
Ruwix 4x4x4 Solution, from: http://ruwix.com/twisty-puzzles/4x4x4-rubiks-cube-rubiks-revenge
Ruwix Parity, from: http://ruwix.com/twisty-puzzles/4x4x4-rubiks-cube-rubiks-revenge/parity
Speed Solve Parity, from: http://www.speedsolving.com/wiki/index.php/4x4x4_Parity_Algorithms
MZRG SiGN Notation Page, from: http://www.mzrg.com/rubik/nota.shtml
Wikipedia Page, from: http://en.wikipedia.org/wiki/Rubik%27s_Revenge
Sebesteny Patent, from: www.uspto.gov - patent no. 4,421,311
Li Patent, from: www.uspto.gov - patent no. 5,992,850


Made in China 2012.
(plastic, 2.75 inches;
blue opposite green, red opposite orange, yellow opposite white)
Here are three consecutive 90 degree turns:





Made in China 2012.
(plastic, 2.8 inches;
blue opposite green, red opposite orange, yellow opposite white)
Here are three consecutive 90 degree turns:




Made in China, 2011.
(plastic 2.3" x 2.3" x 2.9";
blue opposite green, yellow opposite white, red opposite orange)
Turns on the 4x4 planes can be 90 degrees, while turns on the 4x5 planes must be 180 degrees; Jaap's Page presents a solution.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/cube445.htm




a.k.a. TomZ 4x4x6 Cuboid
Purchased from Mefferts; made by the Now Store, Hong Kong, 2012.
(plastic, 2.5" x 2.5" x 3.5";
orange opposite red, blue opposite green, yellow opposite white)
The shape can change quickly; shown below are three consecutive 90 degree turns. Solution steps are outlined on the Rubik's Ultimate Solution Page.



Further Reading
Jaap's Page,, from: http://www.jaapsch.net/puzzles/cube446.htm
Ultimate Page, from: http://rubiksultimatesolution.blogspot.com/2012/04/4x4x6-cuboid.html
Solution can work pretty much exactly the same as for the Rubik 4x4x4 solution that reduces solving to that of solving a Rubik 3x3x3; which we refer to here:
Phase 1: Match up the centers.Like the Rubik 4x4x4 solution, the same simple sequence can be used over and over to match up the center 3x3 regions. A little more organization for this process helps. Do the yellow face first, turn the cube over and do the other faces one at a time. For all but the last face, first make a column of three that passes through the center, and then for the other two columns, assemble a column of three in an adjacent unsolved face and then add it in (using the same simple sequence). The last face may end up solved after solving the second to last face, but if not and it looks like a complicated situation (e.g., just two squares exchanged between the two faces), don't worry, just perssit with the same simple sequence in different ways until you get them solved. You will likely have to mix up the second to last face as yo do this, and it may be helpful to make use of the variation where you twist the middle row along with the outer two.Phase 2: Match up the edges.Like the Rubix 4x4x4 solution, the same simple sequence can be used over and over to pair edge pieces, except now, first pair two and then pair them with the third piece. When down to the last two to be solved, the same final sequence for the last pair cane be used when the two edges are configured to look like this (where the X's are correct but the middle Y may be flipped):Phase 3: Solve like a Rubik's 3x3 cube.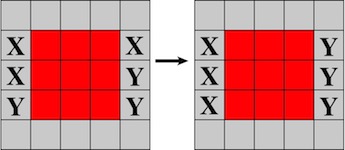 Solve as you would for a standard Rubik's 3x3x3 cube (the edge pairs and the center 3x3 squares stay together as you do the standard U, D, L, R, F, B moves). At this point if you are lucky, the cube is completely solved!
Solve as you would for a standard Rubik's 3x3x3 cube (the edge pairs and the center 3x3 squares stay together as you do the standard U, D, L, R, F, B moves). At this point if you are lucky, the cube is completely solved!
However, although the PLL parity of the Rubik 4x4x4 cube is no longer possible, OLL parity may have to be fixed. The single flipped edge triple will have a correctly oriented center piece and the two pieces to its left and right flipped. In fact, due to the presence of the correct center in a flipped triple, the presence of OLL parity becomes apparent at the end of Phase 2. For example, when referring to the figure above, either the center Y piece is flipped on the left (and things work out ok) or it is not and ends up flipped on the right.
Meffert's Page, from: http://www.mefferts.com/puzzles/profsol.html
Jaap's Page, from: http://www.jaapsch.net/puzzles/cube5.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/rp/RubPro1.htm
Monroe's Page, from: http://www.geocities.com/alchemistmatt/cube/5by5cube.html
Instructables Page, from: http://www.instructables.com/id/How-to-solve-a-5x5-Rubiks-Professor-cube
Ruwix Page, from: https://ruwix.com/twisty-puzzles/5x5x5-rubiks-cube-professors-cube
Simply Rubik Page, from: http://rubik.rthost.org/5x5x5_edges.htm
wikiHow Page, from: https://www.wikihow.com/Solve-a-5x5x5-Rubik%27s-Cube
Wikipedia Page, from: http://en.wikipedia.org/wiki/Professor's_Cube
Krell Patent, from: www.uspto.gov - patent no. 4,600,199
Li Patent, from: www.uspto.gov - patent no. 6,129,356
Verdes Patent Application, from: www.uspto.gov - patent application 2007/0057455

a.k.a. V-Cube 6x6x6
Patented by P. Verdes 2007, made by V-Cube 2008.
(plastic, 2.75 inches;
opposite black is yellow, opposite red is orange, opposite blue is green)
Uses slightly rectangular cubes on the edges and larger square cubes at the corners; works with a click-stop action. The Verdes patent describes designs as large as 11x11x11. Below are photos of the this puzzle partially disassembled and the pieces that are used; note that some of these pieces are used for filling space that is not seen from the outside. The reduction to a Rubik 3x3x3 solution used for Rubik 4x4x4 and Rubik 5x5x5 solutions can be used for solving this cube.



Further Reading
Jaap's Page,, from: http://www.jaapsch.net/puzzles/cube6.htm
Wikipedia Page,, from: http://en.wikipedia.org/wiki/V-Cube_6
Verdes Patent Application, from: www.uspto.gov - patent application 2007/0057455
Verdes Patent, from: www.uspto.gov - patent no. 7,600,756

a.k.a. V-Cube 7x7x7
Patented by P. Verdes 2007, made by V-Cube 2008.
(plastic, 3.1 inches;
opposite black is yellow, opposite red is orange, opposite blue is green)
This cube has a slightly bulging shape. The V-Cube 7x7x7 on the left is described in the same patent as the V-Cube 6x6x6 (the patent describes designs as large as 11x11x11), and like that cube, it uses slightly rectangular cubes on the edges and larger square cubes at the corners (the 7x7x7 has continuous action, whereas the 6x6x6 has click stop action).
The reduction to a Rubik 3x3x3 solution used for Rubik 4x4x4 and Rubik 5x5x5 solutions can be used for solving this cube.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/cube7.htm
Wikipedia Page, from: http://en.wikipedia.org/wiki/V-Cube_7
Verdes Patent Application, from: www.uspto.gov - patent application 2007/0057455
Verdes Patent, from: www.uspto.gov - patent no. 7,600,756






Made in China, 2010 - 2013.
(8x8x8: plastic, 3+1/4", red opposite orange, yellow opposite white, blue opposite green,
9x9x9: plastic, 3+3/4", yellow opposite gray, orange opposite red, blue opposite green,
10x10x10: plastic, 3+7/8", yellow opposite white, red opposite orange, green opposite blue,
11x11x11: plastic, 4+1/2", yellow opposite black, orange opposite red, blue opposite green)
The patent for the Rubik 6x6x6 and Rubik 7x7x7 cubes presented designs for up to 11x11x11 cubes. Subsequently 8x8x8 through 11x11x11 cubes were mass produced in China. The even dimension 8x8x8 and 10x10x10 cubes shown on top above are square in shape but with larger edge and corner tiles, and the odd dimension 9x9x9 and 11x11x11 cubes shown on the bottom above are also slightly curved in shape.
The reduction to a Rubik 3x3x3 solution used for Rubik 4x4x4 and Rubik 5x5x5 solutions can be used for solving these larger cubes.
Further Reading
Chris Hardwick's Page On Big Cube Speed Cubing, from:http://www.speedcubing.com/chris/bigcubes-info.html


YongJun MoYu 13 Layer, made in China, 2015.
(plastic, 5+1/4", over 1000 pieces, weighs 5+1/3 pounds)
This cube goes improves the 11x11x11 design with extra tabs on the ends of some pieces. Tony Fisher does an impressive job in a video showing a complete disassembly of the cube, and a second video showing a reassembly; he identifies 38 piece classes.
Even larger Rubik's cubes have been custom made with 3D printing. In February 2011 Oskar Van Deventer presented a Rubik 17x17x17 cube called "Over The Top" (using Shapeways 3D printing technology), In 2016 Coren Puzzle made a 22x22x22 cube), with 2,691 pieces, and in 2017 Grégoire Pfennig demonstrated this 33x33x33 cube with 6,153 pieces (and 6,534 stickers):

The reduction to a Rubik 3x3x3 solution used for Rubik 4x4x4 and Rubik 5x5x5 solutions can be used (in principle, with enough patience) for solving large cubes of any size.
Further Reading
Tony Fisher Disassemble,, from: https://www.youtube.com/watch?v=JlbsR--UVf8
Tony Fisher Reassemble,, from: https://www.youtube.com/watch?v=xP8AdF8Tl-w
Deventer presentation February 2011, from:http://twistypuzzles.com/articles/building-17x17x17/building-17x17x17.pdfShapeways Page, from: http://www.shapeways.com
Rubik 17x17x17 Video, from: http://www.youtube.com/watch?v=ihWyzvOM9pk
Rubik 17x17x17 Disassembly Video, from:http://www.youtube.com/user/OskarPuzzle?blend=2&ob=1#p/u/2/CBY7JRh2YOoRuwix Page about the 22x22x22 cube, from:https://ruwix.com/the-worlds-largest-cubic-nxnxn-rubiks-cube-puzzle-22x22x22Ruwix Page about the 33x33x33 cube,, from: https://ruwix.com/33x33x33-rubiks-cube
Greg's 33x33x33 video,, from: https://www.youtube.com/user/RubixFreakGreg


Made in China by WitEden, 2012.
(plastic, 2.25" square; white opposite yellow, green opposite blue, red opposite orange)
Looks at first like a Rubik 3x3x3 cube with unequal sections; but turns so as to realign the center planes in a way that causes shape to change quickly; here are three successive 90 degree turns:





Made in China by WitEden, 2012.
(plastic, 2.7" x 2.7" x 2.25"; white opposite yellow, green opposite blue, red opposite orange)
A larger version of the Camouflage Cube 3x3x3 where turns realign the center planes in a way that causes shape to change quickly; here are three successive 90 degree turns:




Made by Fabio Causarano, 2007.
(plastic, 2 by 3 by 4 inches)
Constructed by combining Rubik's cube mechanisms. In only a few twists the puzzle can become quite jumbled; here is an example of a sequence of four moves:




Referring to the diagram on the right above (which uses the colors gray, orange, and blue to denote the three portions of the puzzle), the center four gray cubes form a solid block to which two essentially separate puzzles are attached; each of the two 2x3 orange sections can be rotated (by temporarily rotating blue out of the way to solve the orange portion independent of the blue, and similarly the blue portion works independent of the orange. The colors are useful to help think about what is going on (although it is not necessarily the case that the colors will be correct whenever the puzzle has the correct shape).

Made by Fabio Causarano, 2007.
(plastic, 1.4 inches)
Like the Evil Cuboid 2x3x4, constructed by combining Rubik's cube mechanisms. Here is an example of a sequence of four moves:






Made by Fabio Causarano, 2007.
(plastic, 2.2 by 2.9 by 3.7 inches)
Like the Evil Cuboids 2x3x4, constructed by combining Rubik's cube mechanisms. Here is an example of a sequence of four moves:




Here is another example of a sequence of 5 moves:







Made in China, 2010.
(plastic, 1.6 inches high by 2.2 inches square,
yellow opposite white, blue opposite green, red opposite orange)
A smaller puzzle in the theme of the Crazy Cube 3x3x3. Each side can be flipped 180 degrees as in a standard Rubik 2x3x3. cube. In the solved state shown above with yellow on top, when grasping the bottom and rotating the top, the yellow face rotates about the center circle. After one flip of an edge, holding the bottom and rotating the top turns the entire top face as with a standard Rubik 2x3x3 cube and rotates the circle in the bottom. Each successive flip of an edge reverses the relative movement of top and bottom. That is, one full side is always connected to the center circle of the other. Here are four successive moves of flip right, rotate top 90 degrees clockwise, flip right, rotate top 90 degrees clockwise:





Crazy Cube Mars, purchased from Mefferts, 2010
(plastic, 2.2 square, white opposite yellow, blue opposite green, orange opposite red;
Crazy Cube 2x3x3 is a smaller puzzle with this theme)
There are two types of faces:Spin Around: The circle in the center stays fixed and the remainder of the face rotates.The Mars member of a series of eight (Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune) that differ in the configuration of the faces; it has the following face configuration:
Spin Together: The entire face moves, as in a standard Rubik's Cube.white = around, yellow = togetherHere is a sequence of three clockwise moves of the left, right, and top faces:
blue = together, green = around
orange = together, red = around




a.k.a. WitEden Super Magic Cube
Made by WitEden, sold by Mefferts 2011.
(plastic, 2.25" x 2.25" x 1.75"; also sold in a white body)
In the same theme of Rubik's Cube 3x3x3 generalized to the Crazy Cube 3x3x3, this puzzle generalizes the WitEden 3x3 stacks (that were made as large as 3x3x9) to have the added movement. For this one, the circle turns with the top layer, and the bottom layer turns around the circle; a version was also made where both the top and bottom layers turn around the circle.

Made in China, 2010.
(plastic, 2.6" square, white opposite yellow, blue opposite green, orange opposite red;
Crazy Cube 2x3x3 and Crazy Cube 3x3x3 are smaller versions;
Crazy Cube 4x4x4 Two has a larger center circle)
Faces rotate around the center circle; here is a sequence of three face rotations:



Here is a sequence of 4 rotations about the center:




Jaap's Page presents a solution.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/crazy444.htm

Made in China, 2010.
(plastic, 2.6" square, white opposite yellow, blue opposite green, orange opposite red;
Crazy Cube 2x3x3 and Crazy Cube 3x3x3 are smaller versions;
Crazy Cube 4x4x4 Crazy Cube Two 4x4x4 has a smaller center circle)
Faces rotate around the center circle; here is a sequence of three face rotations:



Jaap's Page presents a solution.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/crazy444.htm

Designed by Oskar van Deventer, made by Witeden, purchased from Amazon.com 2014.
(plastic, 2+9/16" square)
A Rubik 3x3x3 cube generalized so that the middle section can turned by 45 degrees. The designer says this on the Shapeways Page:"Mixup Cube is like a Rubik's Cube, but with an unexpected twist. When a mid plane is turned by 45 degrees, other turns are possible. This way of turning mixes up the center and edge pieces. Although the concept has already been patented in 1985 by Sergey Makarov, this version has an internal 2x2x2 "cube" for extra stability."Here is a 45 degree turn of the middle followed by a 90 degree turn of the front followed by a 90 degree turn of the left side:



Further Reading
Shapeways Page, from: http://www.shapeways.com/model/31732/mixup-cube.html



Designed by Adam G. Cowan, purchased from Mefferts 2014.
(plastic, 2.2 inches, left silver edition, middle stickered edition,
right stickered version with three turns)
The Meffert's Page says"The ghost cube is an exercise in making a 3x3x3 shape modification that is as challenging as possible while only allowing one solution. Misaligned layers, odd shaped pieces, and only one color all add to the challenge."and it quotes the designer:"When I designed this puzzle back in 2008, I was inspired by Tony Fisher's Golden Cube, itself an iconic puzzle. The Ghost Cube design gradually formed over several days of 'tweaking' a basic concept until I had something really interesting. The very first prototype was printed by Geert Hellings and shown at DCD 2008 with good reviews, and early in 2009, several were made for sale by Jason Smith. After the initial sales, the Ghost Cube concept sat on the back shelf for a while, and to my surprise, several puzzle builders created their own hand made versions (including a 7x7x7 version!). Suddenly there was a strong desire to produce this puzzle, and I set to work on an injection molded production design. I am very happy with the results, and glad that I will be able to share this puzzle with the entire puzzle community! Enjoy!"


Designed by Justin Eplett, purchased from Mefferts 2013.
(plastic, 2.25" square; smooth mechanism;
left 2 color version, right 4 color version)
The off-axis points of rotation combined with two sizes of cubes, allows for jumbled shapes to be formed; for example, here are three consecutive 90 degree turns:




Designed by Adam G. Cowan, purchased from Mefferts, 2010.
(plastic, 2.2 inches;
yellow opposite white, green opposite blue, orange opposite red)
This puzzle works like a Rubik's 3x3x3 Cube where looking at each face there are three layers that can turn. Here are two views from the top of the two layers turned.


Any move makes a non-square shape, and successive moves make a completely jumbled shape. Here is a sequence of three moves, a clockwise rotation of the back layer, followed by a clockwise rotation of the front layer, followed by a clockwise rotation of the lower right layer:




a.k.a. Pyraminx Cube
Purchased from Meffert's 2007.
(plastic, 2.2 inches)
Here is a photo of the other three sides:

It can be rotated along any of the planes that passes diagonally through the cube:



Jaap's Page credits this puzzle to Tony Durham, says that it was originally called the Pyraminx Cube by Uwe Meffert, that Douglas Hofstadter coined the name Skewb in a 1982 Scientific American article, discusses the relationship of the Skewb to the Pyraminx, and presents a solution. There are a number of variations of this puzzle, including the Skewb Diamond, Super Skewb Diamond, Skewb Ultimate, Skewb Kite, 3D Skewb, and Skewb Ball
Further Reading
Meffert's Page, from: http://www.mefferts.com/puzzles/skewbsol.html
Jaap's Page, from: http://www.jaapsch.net/puzzles/skewb.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/Skewb.htm
Dry Erase Board Page, from: http://www.thedryeraseboard.com/mechpuz/skewb/solution
A Cubist Page, from: http://www.acubist.com

Augmented Faces Skewb
a.k.a. Polymorphix Limited Edition
Purchased from Meffert's 2008.
(plastic, 2.9 inches)
Same as the Skewb where each face has a protruding piece on it. The colors of each of the four faces of a protrusion must match the color of the corresponding adjacent face, which gives an explicit constraint to the orientation of a face with respect to its corners.

Augmented Corners Skewb
a.k.a. 3D Skewb
Purchased from Meffert's 2008.
(plastic, 2.9 inches)
Same as the Skewb where each corner has been replaced with a protruding piece (that has the same three colors that match the adjacent faces).
a.k.a. Void Skewb
Designed by Tony Fisher, purchased from Mefferts 2010.
(plastic, 2.2 inches)
In the theme of the Rubik 3x3x3 Void Cube, same as the Skewb but without the centers, so that one can look through the center of the cube along any of the three axes (i.e., a square bar can be passed through the cube in any of the three directions).

Designed by David Pitcher, purchased from Mefferts, 2015.
(plastic, 2+3/4" square)


Designed by Tony Fisher, purchased from Meffert's, 2009.
(plastic with metallic finish, 3.1 inches;
made in a number of colors in addition to gold,
including silver shown above, copper, white, black)
A Skewb mechanism with sections offset; makes a big mess when it is mixed up. In the same spirit as the Rubik 3x3x3 Mirror Block pieces of the cube are distinguished by shape rather than color.


Designed by David Pitcher, 2017.
(plastic made with a 3D printer and custom stickers, 2.25 inches square,
red opposite purple, blue opposite green, yellow opposite orange,
left custom 3D print by David Pitcher, right purchased from Amazon 2019)
A fun to use puzzle with smooth movement. Like the Dino Cube, corners can twist. However, here only half of them can, where the spots in the middle of the three faces move with the face. It is easy to play with the puzzle until the edges are all correct, and then four move sequence can then be used to permute the spots.
As shown on the left below, consider a solved cube with green on the top face, yellow on the front face, purple on the right face, and red on the left face (which cannot be seen here). Refer to the lower left corner of the front as LL, the upper right corner of the front as UR, let cw denote a clockwise rotation of a corner, and cc a counter clockwise rotation. These four corner rotations move the front spot to the right, the right spot to the left, and the left spot to the front. By repositioning and performing this sequence a number of times the puzzle can be solved.

LL cw
UR cw
LL cc
UR cc
Further Reading
Six Spots Twisty Puzzles Museum Page 2019, from: http://www.twistypuzzles.com
Twisty Puzzle Pitcher Puzzles museum pages 2019, from: http://www.twistypuzzles.com




a.k.a. Dinosaur Cube
Described in patent of J. Holloway 2000, first manufactured in the mid 1990's,
left: custom made from a Rainbow Cube mechanism by D. Calvo 2007,
middle two: sold by SMAZ 2011,
right: sold by Mefferts 2011 (a similar cube made by Mf8 and sold on Amazon.com 2018).
(All are plastic, left 2.3 inches, others 2.2 inches,
left three: yellow opposite orange, pink opposite red, blue opposite white
right: yellow opposite white, blue opposite green, red opposite orange)
Each corner can twist. Below are photos of the other three sides and of the puzzle mixed up:


Next to Six Spots (which can be viewed as a simplier version of the Dino Cube) and Pyraminx Duo, the Dino Cube is one of the most easy (but fun) Rubik's type puzzles. Hold the cube with one corner facing up and determine what colors must go on what faces. Start by solving just this upward facing corner. Then do the three adjacent corners to it. Finally, the corner facing down may just need to be rotated. Three-deep reasoning can be used, like "to rotate this triangle into place, I need to first rotate this corner so it doesn't get messed up (and then rotate it back afterwards), and before doing that I should rotate this other corner so it doesn't get messed up (and rotate it back afterwards)". This reasoning works because you don't care what happens to the bottom corner until the end, when it will end up solved except for rotating it.
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/dinocube.htm
Holloway Patent, from: www.uspto.gov - patent no. 6,056,290



a.k.a. Black Flower Cube, Star Cube, Rex Cube
Made in China, 2010.
(plastic, 2.2 inches;
white body: yellow opposite black, blue opposite green, red opposite orange;
block body: yellow opposite white, blue opposite green, red opposite orange)
Generalized Dino Cube, with two paths across each diagonal; here are 3 successive moves:



Designed by Oskar Van Deventer, sold by Mefferts 2011.
(plastic, 2.4 inches;
yellow opposite orange, blue opposite green, red opposite purple)
In the theme of the Dino Cube, but much more complex; corners rotate in two different layers:





a.k.a. Super Cubix, Cube 21
Patented by K. Hrsel and V. Kopsky 1993, copyright Irwin Toys 1990.
(plastic, 2.1 inches)
Three layers that form a cube when solved. The middle layer has two identical trapezoid pieces that can be in only one of two states, square or nonsquare. The top and bottom each have four 60 degree corner pieces and four 30 degree edge pieces. The only moves are to rotate the top or bottom layers by a multiple of 30 degrees and to make a vertical 180 degree twist along the reference plane that passes through the two middle pieces. The middle can be solved independent of top and bottom. Repeating three times a twist followed by a 180 degree rotation of the top changes the state of the middle (if you don't care about disturbing the top and bottom, a single 30 degree rotation followed by a twist suffices). A twist followed by 180 rotations of the top and bottom, followed by a twist flips the middle upside-down. And we can rotate the top and / or bottom after a sequence of moves to align them with the middle. Hence, we address solving the top and bottom, without worrying about the middle.
The easier problem of getting the puzzle back to a cube shape, but with colors in any arrangement (as in the second figure above) requires no explicit memorization. Gather the 8 edges in the top to form the "flower" pattern; the figure below shows the flower on the left and patterns resulting from 4 twists. The bottom layer below the flower has all 8 corners arranged in a star, however, the four positions resulting from each of the twists all have identical patters on the top and bottom. So the rule for this sequence is "rotate along the major axis of symmetry 4 times" (shown by the dark lines). The only exception is when a twist gives you the same pattern back; in this case, rotate the bottom by 90 degrees before performing the twist (step 3).

Making the flower is not hard. Pairing edges and then combining pairs is the general approach, but you typically cannot avoid having two "stragglers" that are not paired. The key is to get a pair of stragglers separated by exactly two corner pieces; then you can park them in the bottom left, use rotations of the top and twists to get the other 6 edge pieces together, and then twist up the stragglers to become the first and last of the 8. If you get stuck with two stragglers separated by only one corner piece, split a group and rearrange, sooner or later things will work.
We combine approaches of Jaap, Vandenbergh, and Nerd Paradise for a solution of more moves, but requires only 3 non-trivial sequences to be memorized.
Holding the puzzle: Hold in your left hand with Square 1 on the left, your thumb on the short orange section of the front of the middle layer and your finger on the long red section of the back of the middle layer. All twists are relative to the reference plane that goes from the front left to the back right.
Notation: Pieces are denoted by direction U (up), D (down), L (left), R (right), F (front), B (back); UFL corner, BR edge, etc. For moves, / denotes a twist and (x,y) means rotate the top x units and the bottom y units; a positive number is clockwise and a negative number is counterclockwise. For example:change state of middle layer: (6,0) / (6,0) / (6,0) /Step 1: Make the puzzle into a cube, as described on the previous page.
flip the middle layer: / (6,6) /
Step 2: Get all the white corners to the top and all the green corners to the bottom (but not necessarily in their correct locations). If you are at the level that you can make it into a cube, you can easily do this. Get two green together and park them in the lower left. The using rotations of the top and twists get the other two greens together and twist them down.
Step 3: Get all the white edges to the top and all the green edges to the bottom (but not necessarily in their correct locations), using the transformation UB <-> DF:
(0,-1) / (-3,0) / (4,1) / (-4,-1) / (3,0) /
A note on using the puzzle upsidedown: The moves in Steps 4 and 5 are defined for the top layer. To apply them to the bottom layer, turn the puzzle upsidedown, hold the puzzle with Square 1 on the left (your thumb on the long red section on the front and your finger on the short orange section on the back) and precede a move sequence with (-1,1), which restores the reference plane to effectively go from front left to back right.
Step 4: Position corners using the transformation UFL <-> UFR:
/ (3,-3) / (3,0) / (-3,0) / (0,3) / (-3,0) /* Three times to swap diagonally, or do directly using UBL<->UFR:Step 5: Position edges using the transformation UF <-> UR:
/ (3,3) / (3,0) / (3,3) / (3,0) / (3,3) /
/ (-3,0) / (0,3) / (0,-3) / (0,3) / (2,0) / (0,2) / (-2,0) / (4,0) / (0,-2) / (0,2) / (-1,4) / (0,-3) /* Three times to swap opposites, or do directly using UL<->UR:Step 6: Fix the middle layer if necessary.
/ (3,3) / (-1,0) / (2,-4) / (4,-2) / (0,-2) / (-4,2) / (1,-5) / (3,0) / (3,3) /
Exchange the top and bottom layers:/ (6,6) / (5,-5)Exchange the UF and UB edges with DF and DB (Nerd Paradise "Sequence A"):(1,0) / (-1,-1) / (0,1)Exchange the 4 top edges with the 4 bottom edges:(1,0) / (-1,-1) / (-2,-2) / (-1,-1) / (0,1)Exchange two pairs of corners (from Jaap's page):UFR<->UBL, DFR<->DBR: / (3,0) / (-3,0) / (3,0) / (3,0) / (6,0) /Exchange two pairs of edges (from Jaap's page):
UFR<->UBR, DFL<->DBR: / (0,-3) / (0,3) / (0,-3) / (0,-3) / (0,6) /UF<->UB, DF<->DB: (1,0) / (-1,-1) / (6,0) / (1,1) / (-1,0)Exchange two edge corner pairs (Nerd Paradise "Sequence B"):
UL<->UF, DR<->DF: (1,0) / (-3,0) / (-1,-1) / (3,0) / (1,1) / (-3,0) / (-1,-1) / (4,1) / (-1,0)DL<->DR, DLB<->DRB: / (3,0) / (-3,-3) / (0,3) /
Square 1 is shipped mixed up in a way that looks intimidating but can be solved with 7 twists that are provided in the directions:
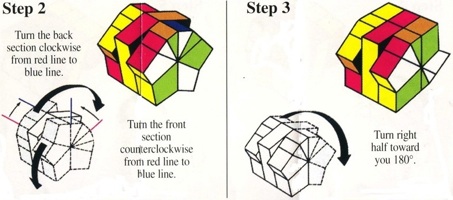
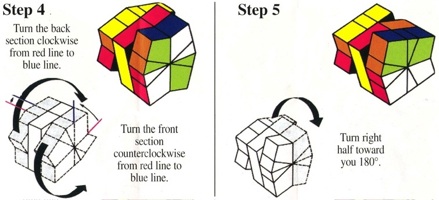
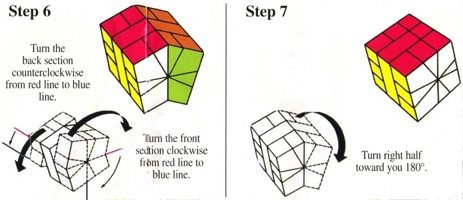


Left: Purchased from Mefferts 2012.
Right: "Dodecagonal Barrel", custom made by Laurent Langlade 2007.
(plastic, made with Square 1 parts; 2.2 inches;
top and bottom layer can each rotate by multiples of 30 degrees
and a vertical 180 twist can be made along a single reference plane)





"Super Square 1", by Smaz Smart Toy Shop IQ Toys, Hong Kong, 2008-2009.
(plastic, 2.2 inches high;
extra center layer where everything rotates around a center post that splits;
switching top and bottom layers will not change color of the top of the posts.)

"Two-Layer Square 1, made in China 2011. (plastic, 2.2" x 2.2" x 1.1", a Super Square 1 without the middle layers)
Further Reading
Jaap's Page - Square 1, from: http://www.jaapsch.net/puzzles/square1.htm
Jaap's Page - Square 2, from: http://www.jaapsch.net/puzzles/square2.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/sq1/sq1xf.htm
McFarren's Page2, from: http://www.geocities.com/abcmcfarren/math/sq1/sq1xf.htm
Alchemistmatt Page Page, from: http://www.alchemistmatt.com/cube/square1.html
Dry Erase Board Page, from: http://www.thedryeraseboard.com/mechpuz/square1/solution
Nerd Paradise Page, from: http://nerdparadise.com/puzzles/square1
Vandenbergh's Page, from: http://www.cubezone.be/square1.html
Monroe's Page, from: http://www.alchemistmatt.com/cube/square1.html
Eggermont's Page, from: http://web.inter.nl.net/users/C.Eggermont/Puzzels/SquareOne
Eggermont's List of all Square 1 configurations,from: http://web.inter.nl.net/users/C.Eggermont/Puzzels/SquareOne/SquareList.htmlF2 Page, from: http://f2.org/maths/square1
Hrsel and Kopsky Patent, from: www.uspto.gov - patent no. 5,193,809


Designed by A. Cowan 2005, purchased from Mefferts, 2010.
(plastic, 2+3/8 inches;
black body: red opposite white, yellow opposite orange, blue opposite green
white body: red opposite black, yellow opposite orange, blue opposite green)
Each of the 12 edges can rotate 180 degrees; here is a sequence of three moves:



In addition, an edge may be partially rotated so that subsequent moves create a jumbled shape; here is the same sequence of three moves as shown above except the first is a partial rotation:



Designed by Tom van der Zanden, purchased from Mefferts, 2012.
(plastic, 2+3/8 inches;
red opposite orange, yellow opposite white, blue opposite green)
A curvy version of the Helicopter Cube:




Designed and custom made by Oskar Van Deventer, 2012.
(plastic, made on a 3D printer, 2.3" square;
red opposite orange, yellow opposite white, blue opposite green)
The puzzle has 4 layers where the sides are yellow (front), green (left), blue (right) and white (back). Layer 1 (top) is red on top and layer 4 (bottom) is orange on the bottom. In the top layer there is a 35 tooth center gear, three 10 tooth planet gears, and 55 teeth around the edge. In the bottom layer, using finer teeth, is again a 35 tooth center gear (but of a smaller diameter than the top one), three 21 tooth planet gears, and 78 teeth on the outside. The center gears are fixed to a common axle. The axles for the top planet gears are attached to layer 2. The axles for the bottom planet gears are attached to layer 3.
Basically playing with the puzzle involves confusing rotations seeking least common multiples of numbers based on the gears. Here are general properties:
- Hold the middle two layers and rotate the top layer 7 clockwise 180 degree turns and end up with the top and bottom layers rotated 180 degrees with respect to the middle two layers.
- Hold the bottom layer and rotate the top two layers together 8 clockwise 180 degree turns and end up with layer three rotated 90 degrees clockwise with respect to the other three layers.
- Hold the top layer and rotate the bottom two layers together 18 clockwise (as you look up) 180 degree turns and end up with layer two rotated 180 degrees with respect to the other three layers (9 clockwise 180 degree turns to rotate layer 2 counter clockwise 90 degrees with respect to the top layer and rotate the bottom two layers 180 degrees with respect to the top layer).


a.k.a. David Gear Cube
Designed by David Tzur.
Left: Custom 3D print by Oskar Van Deventer / Shapeways, 2012.
Right: "David Gear Cube" sold by Mefferts 2018.
(plastic, 2.3" square;
yellow opposite white, orange opposite red, green opposite blue)
In the theme of the 3x3x3 Gear Cub, fully functional Rubik 2x2x2 with gears. On the left below the top layer has been turned, in the middle the turning of the top has completed to make the puzzle square again, and on the right the front layer has been turned until the puzzle became square again:




Designed by Oskar van Deventer, purchased from Mefferts, 2014.
(plastic, 2.25" square;
black body: red opposite white, yellow opposite orange, green opposite blue;
white body: red opposite b;ack, yellow opposite orange, green opposite blue)
This geared 2x2 type cube allows 90 degree turns and quickly gets very messy. Starting with the orientation shown above, here is a 90 degree turn of the right side followed by a 90 degree turn of the front:



Invented by Oskar van Deventer, purchased from Mefferts, 2010.
(plastic, 2.3 inches)
Looks like a complicated version of Rubik's Cube, but is actually much easier to solve (see the Gear Cube Extreme for a harder to solve version). Here is the puzzle solved, the right face rotated 90 degrees, and the right face rotated 180 degrees:



Call the operation of rotating a face 180 degrees a flip; it is the only thing you can do:Jaap's Page presents a solution. Here is an approach that requires essentially no memorization:
- A 90 degree rotation of a face locks up the puzzle.
- Middle layers can only be manipulated by flip operations.
- A flip cycles the adjacent middle layer by 90 degrees and rotates its 4 gear edges by 60 degrees each; 3 flips returns the adjacent middle layer to flat, and 12 flips returns you to exactly where you started. A flip also has the effect of reordering two of the gear edges in each of the other two middle layers.
- Centers move around, but gear edges of a middle layer never leave that layer.
Further Reading
- Restore puzzle to be flat (easy - do flips as needed).
- Solve the corners (easy - faces cannot rotate 90 degrees).
- Use step A to solve as much as possible, use Step B, and repeat until solved (repositioning the cube as appropriate):
- Flip the right face clockwise 6 times.
(Exchanges front/rear and top/bottom of the vertical center layer).
- Flip the bottom face clockwise, flip the right face twice clockwise, flip the bottom face counter clockwise, flip the right face twice counter clockwise.
(Exchanges front/rear of vertical center layer and left/right centers.)
Jaap's Page, from: http://www.jaapsch.net/puzzles/gearcube.htm

Purchased from Mefferts, 2017.
(plastic, 2.6" diameter by 2.6" high;
green opposite blue ends, colors clockwise are yellow, purple, orange, red)
In the theme of the Gear Cube, works like a Rubik 3x3x3 Rubik 3x3x3, with gears moving.


Invented by Oskar van Deventer, purchased from Mefferts, 2011.
(plastic, 2.3 inches)
A harder to solve version of the Gear Cube where the edge pieces along the middle layer are not geared; shipped with stickers to go in the black U's below the gears to make a more difficult puzzle that Mefferts calls the "Gear Cube Extreme". Six turns bring the puzzle back to its shape; below are some example moves. Jaap's Page presents a solution.



Further Reading
Mefferts Page, from: http://www.mefferts.com
Jaap's Page, from: http://www.jaapsch.net/puzzles/gearcube2.htm



Designed by Timur Evbatyrov, purchased from Mefferts, 2015.
Another puzzle in the theme of the Gear Cube.
(plastic, 2.25" square)

Designed by Oskar van Deventer and Bram Cohen, made by Mefferts 2011.
(plastic, 2.25 inches)
As shown on the left below, the puzzle spins around (keep spinning and get back to where you started). As shown in the middle below, the difficulty of this puzzle comes from its ability to be split apart along any of the three axes to allow the orientation of two halves to be changed by spinning only one half, as shown on the right below.




Designed by Oskar van Deventer, sold by Mefferts 2012.
(plastic, 3.25" high, each ede is 3.75";
yellow opposite orange, green opposite blue, red opposite purple)
Here are some sample moves:





a.k.a. Gear Mastermorphix
Designed by Oskar van Deventer, sold by Mefferts 2012.
(plastic, 3.25" high, each ede is 3.75";
yellow opposite orange, green opposite blue, red opposite purple)
Here are some sample moves:


Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/gearcube.htm


Designed by Oskar van Deventer, sold by Mefferts 2012.
(plastic, 3.25" high, each ede is 3.75";
plastic, 2.5" face to face;
yellow opposite orange,
blue opposite light blue,
light green opposite green,
white opposite gray,
pink opposite red,
purple opposite light purple)
These two puzzles are the same except for the stickers.
Rotations are limited to rotating a pair of parallel sides. When rotating, the faces do not become flat again until you rotate all the way back to the start. However, this does not prevent other rotations while the sides are not flat. For example, here is rotating the right side a little, then rotating the right side some more, and then rotating the front side a few turns:





Designed by Tony Fisher and Oskar van Deventer; sold by Mefferts 2013.
(Plastic, 2.5" face to face; two versions identical except for stickers; pink opposite red, white opposite gray, yellow opposite orange, light purple opposite dark purple, blue on lower left opposite light blue, light green on lower right opposite dark green)
In the theme of the Gear Cube, gears move, the shape temporary changes, and then returns to normal as you twist along a plane. Starting with it solved and twisting along a single plane restores the shape every two twists and restores the faces to the correct colors every 8 twists. It takes 24 turns to restore both the face colors and have the T. Fisher on the white face and the Oskar on the yellow face in their original orientations.




a.k.a. Timur Gear Corner Turning Octahedron
Sold by Mefferts 2013.
(plastic, each edge is 3";
yellow opposite orange, green opposite blue, red opposite purple)
A geared version of the Octahedron. Here is how it moves:


Designed by Oskar van Deventer, sold by Mefferts 2012.
(plastic, 3" diameter;
yellow opposite orange, green opposite blue, red opposite purple)
Works like the Gear Cube.

Tomy Pyraminx, Patented by Meffert 1981 and Copyright by Tomy 1981;
(back blue, bottom green, 4" along an edge;;
see also Mefferts Jing's Version of this puzzle)
Notation: There are 4 tips, 4 corners that the tips are attached to, and 6 edges. Holding the puzzle with one of the faces towards you, clockwise and counterclockwise rotations of the top, lower left, and lower right corners are denoted by T+, T-, L+, L-, R+, and R-.
An Edges First Solution:
1. Orient the tips (and to stay organized, keep them correct after each step).
2. Place the bottom edges (easy when you don't care about the corners).
3. Rotate the top so that at least one of the three remaining edges is correct, and position the puzzle so that this correct edge is in back.
4. The two front edges will now be in position; if they are flipped, do:R- T- L- T+ L+ R+ T+5. Correct two corners at a time with simple 5-sequences that rotate the two front corners, where here x and y are each either + or -, and 5 means repeat five times:
Note: Memorize +++--- with a twist" The "twist" is that T is in the middle of the -'s and first of the +'s. No need to remember the final T+, that will be obvious.(Lx Ry)5Choose + and - to be opposite the direction you want to go. For example, do L- R+ five times to rotate the front left clockwise (60 degrees) and the front right counter-clockwise. (to correct a single corner, make it and an adjacent corner incorrect and then use a second 5-sequence to correct the two).
If Step 1 is skipped, then after completing Step 2, Step 3 is 1 move, Step 4 is 7 moves, Step 5 is 10 moves to correct two corners or 20 moves to correct 1, 3, or 4 corners, and finally correcting the tips is 3 moves, for a total of 31 moves in addition to Step 2. This is far more than used by an optimal algorithm (Jaap's Page describes a computer analysis that shows that a solution is always possible in at most 11 moves). However, it is a simple method that amounts to memorizing the sequence of 7 moves for Step 4. Also, if one is careful to choose the easiest face for the bottom and minimize the number of moves for Step 2, the solution compares well with the total of 38 moves mentioned in the directions to the original Tomy version:


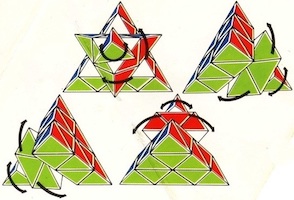
A corners first solution may use fewer moves but is harder to remember; we use the same notation as for the edges first solution:
1. Orient the tips to match their corners.
2. Orient the corners to be correct.
3. Solve the top three edges using ++-- or --++ on adjacent corners. These transformations leave the corners solved, do not disturb two of the top edges, and permute the other edges. With practice it is pretty easy to get the top pyramid of the puzzle solved.
4. Turn the puzzle so that the face with the unsolved three edges faces you. Use these two transformations cycle the three edges clockwise or counter clockwise until the puzzle is solved, or all that is left is to flip the two upper front edges:T- R T R-5. If the two upper front edges need to be flipped, we are now in the same situation as Step 4 of the corners first solution, except use a more complicated transformation that does not disturb the corners:
T L- T- LR T- R- T R- L R L-

a.k.a. Hollow Pyraminx
Sold by Mefferts to celebrate its 50th Anniversary, 2019.
(plastic, 4" along an edge)





up-left: metalized surfaced with click stops, 4" on an edge, Mefferts 2006;
up-right: D-FantiX Qiyi Qiming Stickerless, 4" on an edge, Amazon.com 2017;
down-left: plastic 4" on an edge, Mefferts 2006;
down-right: right plastic with chain, 1.75" on an edge.
Further Reading:
Mefferts Page, from: http://www.mefferts.com/puzzles/pyramsol.html
Jaap's Page, from: http://www.jaapsch.net/puzzles/pyraminx.htm
Ruwix Page, from: https://ruwix.com/twisty-puzzles/pyraminx-triangle-rubiks-cube
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/PyrMin.htm
Dry Erase Board Page, from: http://www.thedryeraseboard.com/mechpuz/pyraminx/solution
Nerd Paradise, from: http://www.nerdparadise.com/puzzles/pyraminx
Monroe's Page, from: http://www.alchemistmatt.com/cube/pyramix.html
Meffert Europena Patent, EP042695A2.

Purchased from Mefferts, 2017.
(plastic, each edge is 3.5", as pictured, back is blue and bottom is green)
A larger version of the classic Pyraminx.






An idea of Rob Stegmann, designed by Oskar van Deventer, purchased from Mefferts 2014.
(plastic, 3.25 inches high, each edge is 3.75" long,
left black body, right white body)
In the theme of a simplified Pyraminx, rotating a corner also rotates the centers.
In addition to the Rubik 1x2x2 cube, this is perhaps the most simple to solve Rubik's type cube that has been mass produced. What makes it a great puzzle is that at first glance it looks like it might be complicated to solve. The puzzle has a fun click stop action where two clicks are used to rotate a corner, giving the illusion that more is going on.
A simple 5 move solution is to pick a color, determine the face that that color must go on, turn two of the corners to that face, use a third turn to put the center color for that face with the third color, use a fourth turn to turn that corner to complete the face, and then finally a fifth turn may be needed to rotate the remaining corner correctly.
This five step solution can be reduced to 4 steps by choosing a color initially that already has one corner turned to its face. Or, if none of the colors is on its face, then one of the colors can be turned into its face with three moves where the third move also turns in the correct center color, and then, like the 5 move solution, a final fourth move can be used to rotate the remaining corner correctly.


Purchased frm Mefferts, 2015.
(plastic, 3" along an edge, 4" tip to tip)
A generalization of the Pyraminx Duo that moves in the same way:




a.k.a. Rounded Halpern-Meier Pyramid
Made by Mefferts, 2010.
(plastic, 4 inches;
left: fluorescence labels - back is orange, bottom is green;
right: Cube Smith labels - back is green, bottom is blue)
This puzzle is like the Pyraminx, except it does not have the tips but does have face centers (triangles). We use the same notation for solving, less any reference to tips.
Notation: There are 4 corners and 6 edges. Holding the puzzle with one of the faces towards you, clockwise and counterclockwise rotations of the top, lower left, and lower right corners are denoted by T+, T-, L+, L-, R+, and R-; 3 means do it three times.
Solution:
- Solve the corners and edges with a solution for the Pyraminx.
Note: Without tips to keep you oriented, it can help to determine the colors of the sides once at the start, and then for the remainder of the solving, keep the puzzle in a fixed orientation with the same side facing down and the same side facing you.
- Use the following transformation, given on Jaap's Page, to fix the centers (it exchanges the front and bottom triangles and the left and right triangles):
( R T R- T- ) 3
Further Reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/PyraminxJing.htm

a.k.a. Crazy Tetrahedron Plus
Purchased from Mefferts, 2011.
(plastic, 3.75 inches)
In the same spirit as the generalization of Rubik's Cube 3x3x3 to the Crazy Cube 3x3x3, this is a generalization of Jing's Pyraminx. Shown above is Meffert's "regular" version that has no restrictions on moves; each face can rotate around the circular portion in its center. Like the Crazy Cube 3x3x3, Meffert's also has produced different move restriction variations, with names of the planets (Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune).

Purchased from Mefferts 2007.
(plastic with plastic tiles, 2.5 inches)
This is the same puzzle as the Pyraminx, without the tips (or the same as Jing's Pyraminx without the centers), and the same solution can be used. The colors are arranged so that the yellow triangle is opposite the blue face, the blue triangle is opposite the yellow face, the red face is opposite a green triangle, and the green face is opposite a red triangle)
Note: Without tips to keep you oriented, it can help to determine the colors of the sides once at the start, and then for the remainder of the solving, keep the puzzle in a fixed orientation with the same side facing down and the same side facing you.

Designed by Timur Evbatyrov, made by Mefferts 2011.
(plastic, edges are 3.6", stands 3.4" high;
yellow, orange, blue, green)
A large version of Pyraminx, here are photos of the three types of rotations:




Designed by Timur Evbatyrov, sold by Mefferts 2010.
(plastic, edges are 3" long;
yellow, blue, orabge back, green bottom)
A generalization of the Pyraminx, where in addition to tips and corner sections that rotate, faces can also rotate:





a.k.a. Supernova
Patented by H. Corbeck and C. Bandelow 1982, G. Obermair 1982;
Left Tomy 1982, right Mefferts tiled version 2009.
(plastic, 2.75 inches between opposite faces)
Twelve sides, each a different color, can each be rotated. Jaap's Page gives a solution, mentions the relationship of this puzzle to Alexander's Star and Impossiball (see also Dogic), and has a discussion of a number of origins of this puzzle.
On opposite sides the Tomy version has:red / greenOn opposite sides the Meffert version has:
blue / magenta
yellow / maroon
white (Tomy graphic in center) / orange ("MEGAMINX TOMY" in center)
dark purple / green
light blue / pinklight blue / brownFurther reading:
green / light green
red / orange
white / yellow
purple / pink
blue / dark blue
Meffert's Page, from: http://www.mefferts.com/puzzles/megasol1.html
Jaap's Page, from: http://www.jaapsch.net/puzzles/megaminx.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/mm/MegMin1.htm
Dry Erase Board Page, from: http://www.thedryeraseboard.com/mechpuz/megaminx/solution
Corbeck and Bandelow GB Patent, from: http://www.ipo.gov.uk - patent no. GB2101491
Obermair DE Patgent, from: www.epo.org - patent no. DE3204033
Wikipedia Page, from: http://en.wikipedia.org/wiki/Megaminx

Mefferts 2009.
(plastic, 2.75 inches between opposite faces)
Like the standard Megaminx but with no center portion; in the same theme as the Void Cube.
On opposite sides the colors are:light blue / orange
green / light green
brown / red
white / yellow
purple / pink
blue / dark blue


a.k.a. Crazy Megaminx
Purchased from Mefferts, 2011.
(plastic, 3.1 inches from face to face)
In the same spirit as the generalization of Rubik's Cube 3x3x3 to the Crazy Cube 3x3x3, this is a generalization of the Megaminx. Shown above is Meffert's "Saturn" version, where for each pair of opposite faces, one rotates around the circle in the center (denoted on the packaging as a "0") and for the opposite side the circle rotates with the face (denoted on the packaging as a "1"); the faces and their colors are:white = 0 opposite gray = 1,Like the Crazy Cube 3x3x3, Meffert's also has produced different move restriction variations, with names of the planets (Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune).
red = 1 opposite orange = 0,
green = 1 opposite light green = 0,
blue = 1 opposite light blue = 0,
light yellow = 0 opposite yellow = 1,
pink = 0 opposite purple = 1


a.k.a. Flowerminx
Sold by Mefferts 2009.
(in black and white bodies, plastic, 2.9 inches between opposite faces)
Twelve sides, each a different color, can each be rotated. A simpler version of the Megaminx (see also the Master Kilominx). Here are views of the other six sides:


Both versions use the same colors, except the white face is changed to black when going from the black body to the white body version; on opposite sides the colors are:red / gold
blue / light blue
orange / light purple
yellow / white or black
pink / purple
light green / dark green
Jaap's Page notes that this is the same puzzle as the Impossiball and presents a solution.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/impossi.htm


Made by mf8, sold by Mefferts 2012.
(plastic, 3.4 inches between opposite faces, with storage bag 7.4" x 5.75")
Rotations through the center work like the standard Kilominx (where the puzzle stretches a bit); there is an additional layer on all faces that can rotate.
On opposite sides the colors are:white opposite gray
green opposite light green
blue opposite light blue
pink opposite purple
light yellow opposite yellow)

Made by Cube 4 You (C4U), 2009.
(plastic, 3.5" between opposite faces, 4.2" between farthest points)
A larger version of the Megaminx; twelve sides of distinct colors each have two layers that can be rotated.
On opposite sides the colors are:white (with C4U logo in center) / gray
light blue / dark blue
dark yellow / light yellow
light green / dark green
orange / red
purple / pink

Made by Cube 4 You (C4U), 2009.
(plastic, 3.5" between opposite faces, 4.2" between farthest points)
An even larger version of the Megaminx than the Gigaminx: twelve sides of distinct colors each have three layers that can be rotated.
On opposite sides the colors are:white (with C4U logo in center) opposite brown
yellow opposite aqua
blue opposite light blue
purple opposite pink
light green opposite dark green
orange opposite red


Made by Mefferts 2008.
(plastic, in both black and white bodies, 3.5 inches)
Twelve axes of rotation in a similar theme to the Megaminx, but different because here, each of the twelve faces is rotated along a plane that passes through the center of the puzzle. The six faces shown above are orange, green, blue, purple, brown, and white; as shown below, opposite these faces are the colors teal, dark green, dark blue, pink, burgundy, and yellow:


Jaap's Page presents a solution.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/pyracrys.htm


Made in China by MF8, 2012.
(plastic, 3.5" between opposite faces, each edge is 1+5/8";
black opposite gray,
green opposite light green,
blue opposite light blue,
red opposite light red,
pink opposite purple,
yellow opposite orange)
In the theme of the Helicopter Cube, edges twist:


Purchsed from Mefert's 2007.
(plastic, 2.5 inches between faces, 4 inches point to point,
opposite faces are light blue / blue, yellow / white, green / light green, red / orange)
Rotation is not about the points of the diamond; rather it is along each of the four planes that cuts the puzzle in half. This puzzle is a variation of the Skewb (it is a smaller version of the Super Skewb Diamond). Jaap's Page presents a solution that is a bit more efficient that applying his solution for the Skewb.
Further Reading
Meffert's Page, from: http://www.mefferts.com/puzzles/solution-skewb-diamond1.html
Jaap's Page, from: http://www.jaapsch.net/puzzles/diamond.htm

a.k.a. Diamond Octahedron
Purchased from the Cuber Shop, Tiawan, 2009.
(plastic, 2.25 inches between faces, 4 inches point to point,
opposite faces white / yellow, orange / black, magenta / blue, green / red)
A larger version of the Skewb Diamond; this is a different puzzle than the Octahedron. Rotation is not about the points of the diamond; rather it is along each of the four sets of two planes that divide the puzzle between opposite faces:


a.k.a. Pyraminx Ball
Purchsed from Mefert's 2008.
(plastic, 3 inches between opposite faces)
There are twelve faces and six colors (red, blue, green, orange, yellow, and pink). When solved, each pair of opposite faces is the same color. Like the Skewb Diamond, rotation is not about the points, rather it is along each of the four planes that cuts the puzzle in half, and this puzzle is a variation of the Skewb. However, Jaap's Page explains that this puzzle is harder because orientation of the components of a face matters, and presents a solution. Mefferts also made this puzzle in a 12 color version (yellow opposite white, light green opposite dark green, pink opposite purple, orange opposite light purple, gold opposite red, light blue opposite dark blue); here are views of the front and back:


Further Reading
Meffert's Page, from: http://www.mefferts.com/puzzles/solution-skewbultimate1.html
Jaap's Page, from: http://www.jaapsch.net/puzzles/ultimate.htm


Designed by Tony Fisher, Purchased from Meffert's 2010.
(plastic, 12 sides, 3" between faces, 4" between farthest points;
uses the Skewb mechanism;
left black body, right white body;
yellow opposite orange,
light green opposite dark green,
light blue opposite dark blue,
gray opposite white,
red opposite pink,
dark purple opposite light purple)

Designed by Tony Fisher, purchased from Mefferts 2010.
(plastic, 2.5" between hex faces, 3" between square faces;
based on the Skewb;
6 square faces are dark green;
8 hex faces are yellow opposite orange, purple opposite pink,
red opposite light green, blue opposite light blue)

Purchased from Mefferts, 2009.
(plastic, 2 inches across minimum dimension;
2.75 inches across farthest points)
Like Rubik's 2x2x2 Rubik's 2x2x2 cube with each corner cut diagonally in half so that the three corner faces become a single face. It is shipped with a solved state of two adjacent yellow faces, two adjacent red faces, two adjacent green faces, and two adjacent blue faces. Mix it up, and then any solution method for Rubik's 2x2x2 can be used.


a.k.a. Figurenmatch, Distortion Demon Square
Patented by Manfred Fritsche 1983.
left: shiny stickers 2007, other sides are red and green, plastic, 3.8";
right: Mefferts keychain purchased 2007, plastic, 2.25" edges)
This puzzle is manipulated by turning along a cutting plane (the tips don't turn). It can be hard to visualize what is going on after the puzzle gets into some strange shapes. It is fairly easy to get it back to the pyramid shape; Meffert's Page, Jaap's Page, and McFarren's Page present solutions where this is the first step, but then the final steps employ transformations that temporarily go through non-pyramid shapes. Using a plain colored version of this puzzle, here are some photos of some of the shapes the puzzle can take.





Further Reading
Mefferts Page, from: http://www.mefferts.com/puzzles/jpmsol.html
Jaap's Page, from: http://www.jaapsch.net/puzzles/pyramorf.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/pmorph.htm
Wikipedia Page, from: http://en.wikipedia.org/wiki/Pyramorphix
Fritsche DE Patent, from: www.epo.org - patent no. DE3245341

a.k.a. Star of David, Sterns Puzzle
Patented by I. Goldfarb 1985 and B. H. Apsan 1995,
custom made by EBay member jamf55 in Spain 2007.
(plastic, 2.5 inches)
This puzzle is like a Pyramorphix with a pyramid glued to the center of each of its faces, and the same solution sequences can be used; the colors on this one are arranged so that it is solved when the planes induced by the pyramids each are a single color. Here is a photo of the other sides:

Further Reading
Goldfarb Patent, from: www.uspto.gov - patent no. 4,496,155
Apsan Patent, from: www.uspto.gov - patent no. 5,386,993




a.k.a. Master Pyramorphinx
Left two: made by Mefferts 2009;
right two: made by Smaz Smart Toy Shop IQ Toys, Hong Kong, 2009.
(plastic, left 3.8 high", right three 2.75" high;
left three all have the colors yellow, green, red /orange, blue)
A big brother to the Pyramorphinx. Each of the 6 edges of this puzzle can twist. If one stays limited to 180 degree turns of the edges, then this is a puzzle of mixing up the colors and then restoring them, where the puzzle always has its correct shape. However, the fun begins when you employ 90 degree turns to transform the puzzle into a jumbled mess; here are 4 moves using a black body version from Smaz:





This puzzle works like a Rubik's 3x3x3 cube, where each of the 6 edges corresponds to a face of Rubik's 3x3x3, the four vertices of the Mastermorphinx correspond to 4 non-adjacent corners of Rubik's 3x3x3 (e.g., two diagonally opposite corners on top and two diagonally opposite corners in the other direction on the bottom), and the four faces of the Mastermorphix correspond to the other 4 corners of Rubik's 3x3x3 (where a face corresponding to a corner includes a triangular half of each of the three faces incident to that corner). That is, imagine the 6 edges of the Mastermorphix running diagonally across each face of the 6 faces of the cube, where the 6 center pieces of the edges of the Mastermorphix correspond to the 6 centers of the cube, the 4 tips of the Mastermorphix together with the four centers of the Mastermorphix correspond to the eight corners of the cube, and the remaining 12 face sections of the Mastermorphix correspond to the 12 edges of the cube). So any solution for Rubik's 3x3x3 can be used, but in practice this puzzle can be very connfusing when mixed up into a jumbled shape, until one gets used to looking at it. In a theme similar to the Skewb Egg, just getting the shape back with the single color gold version is a challenge.


Designed by Traiphum Prungtaengkit, purchased from Mefferts 2013.
(plastic, 3.3" along an edge, box is 2.5" square)
A tetrahedron in the theme of a Dino Cube where the tips can twist, but also with the added ability to turn faces; here are three successive moves of twisting the top tip counterclockwise, turning the front face, and twisting the top tip clockwise:




a.k.a. Cushion Cube
Circa 1980's?
(plastic, 2.2 inches)
A Rubik's 3x3x3 Cube that has been beveled and employs a different color scheme; a solution method for Rubik's 3x3x3 Cube can be used to solve this puzzle.
The solution is not unique since when the top and bottom sections are rotated, the puzzle remains solved. The stickers around the middle are gold, silver, white, and light blue. The top and bottom tips have white stickers. The eight slanted faces have the colors green, orange, blue, light purple, yellow, dark purple, red, and pink, but the arrangement of these stickers may vary from one puzzle to another.

a.k.a. Polish Cushion
Custom made by Mariusz Dabrowski 2007.
(plastic, 2.2 inches wide, 2.75 inches point to point;
yellow opposite green, orange opposite pink)
A Rubik's 3x3x3 Cube that has been beveled and employs a different color scheme; like the Pillow Cube a solution method for Rubik's 3x3x3 Cube can be used to solve this puzzle.

Made by SOCUBE, Kuala Lumpur, Malaysia, 2009.
(plastic, 2.2 inches)
Like the Pillow Cube, this is the same puzzle as a Rubik's 3x3x3 Cube. However, as the name indicates, it is confusing because when orientated as shown in the photo above, the top and bottom layers do not rotate (e.g., referring to the front left corner, the two white triangles and the red triangle are part of a single piece). To see the correspondence with Rubik's 3x3x3, turn the puzzle on end so the horizontal planes correspond directly to those of a Rubik's 3x3x3 and each pair of vertical parallel diagonal planes correspond to the pairs of vertical planes of Rubik's 3x3x3; that is, this puzzle is like the Rubik 3x3x3 Fisher Cube with shaped sides. Here are photos of the other sides and how the puzzle moves:




Made in Hungary circa 1980's?
(plastic, 2 inches)
A Rubik's 3x3x3 Cube that has been beveled and employs a different color scheme; like the Pillow Cube a solution method for Rubik's 3x3x3 Cube can be used to solve this puzzle.

a.k.a. Diamond Style Puzzler
Rhombi Diamond, purchased 2007.
(plastic with tiled plastic faces, 2.3 inches)
A Rubik's 3x3x3 Cube that has been beveled like the Pillow Cube and the Hungarian Diamond but uses a simpler color scheme like the Layered Rubik's 3x3x3 Cube; same solution can be used.
This is a fun puzzle that is much easier than the standard Rubik's Cube. It has a nice feel and works very smoothly if lubricated when it is first received (in a few places use a small screwdriver in a crack to make a small opening to squirt in some silicone grease).
Note: It works just like a Rubik's Cube; you must remember to rotate layers 90 degrees at a time, even though the puzzle may look ok after a some 45 degree rotations. If the puzzle seems to be jammed and cannot rotate along a particular axis, don't worry, it is probably because of 45 degree rotations (e.g., the right side will not turn because the top and the bottom layers have been turned 45 degrees); just try some 45 degree rotations until the puzzle works again.
This puzzle was made with any of the three colors in the middle. Below are two unopend ones in the other colors, and also on the right is an earlier version of this puzzle:

Rhombi Diamond,
with orange middle.
Rhombi Diamond,
with white middle.
Diamond Style Puzzler,
circa 1980's.
(plastic with stickers, 2.1")
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/diamstyl.htm
Brooks Patent, from: www.uspto.gov - patent no. 6,644,665

(This description is for top layer = white, middle layer = yellow, bottom layer = orange.)
1. Solve the middle layer.Easy if you don't care about the rest of the puzzle.2. Solve the top and bottom edges.Easy by using 180 degree front rotations to exchange incorrect edges.3. Solve the bottom back right and bottom back left corners.It is easy to play with top rotations and 180 degree front rotations to make at least one bottom corner orange; rotate this corner to the bottom back right. If the bottom back left corner is white, play some more with these rotations to make the top front left and top front middle orange, then rotate the front 180 degrees to bring these two down, and then rotate the bottom 90 degrees to bring the orange corner to the back right (and making the orange corner that was in the back right now in the back left).4. Solve the remaining incorrect corners.This can be done with just 180 degree rotations of the front (F2) and clockwise or counter-clockwise rotations of the top (U, U-). If you want to memorize a simple transformation, this one exchanges the front top left corner with the front bottom left corner:F2 U F2 U- F2


a.k.a. Magic Octahedron
Patented by C. Hewlett 1984.
(plastic, 1.8 inches between faces, 3 inches point to point,
opposite faces are green / white, yellow / blue, red / orange, magenta / gold)
This puzzle has the look and feel of a generalized Pyraminx. The rotating tips have no effect on solving (the Flowered Jewel is the same puzzle without the tips); each pyramid formed by a tip and the layer below it can rotate (this is a different puzzle than the Super Skewb Diamond). However, mechanically, the Octahedron is equivalent to a Rubik's 3x3x3 Cube without corners (or a Rubik 3x3x3 Edges Only Cube with centers) where there is one tip for each face and one face for each corner. The square on which each tip sits is the center of each face of the Rubik 3x3x3 cube and the center point of each face corresponds to a (missing) corner. The correspondence between the Octahedron and the Rubik 3x3x3 Cube may be easier to visualize by looking at the Full Octahedron which includes the centers on each face. Jaaps Page gives a direct solution.
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/octahed.htm
Hewlett Patent, from: www.uspto.gov - patent no. 4,451,039
Ibrahim Patent, from: www.uspto.gov - patent no. 4,593,908
Abu-Shumays Patent, from: www.uspto.gov - patent no. 4,706,956


Made in Hong Kong, 2010.
(plastic, 1.9 inches between faces, 3.2 inches point to point,
opposite faces are green / dark green, yellow / white, blue / light blue, orange / red)
This puzzle is equivalent to the Octahedron with triangles in the center of each face and without the extra rotating tips (or a Flowered Jewel with triangles in the center of each face). It has the look and feel of a generalized Jing's Pyraminx. However, mechanically, it is identical to Rubik's 3x3x3 Cube, where each of the six points is a center square of a face of the cube, and each of the eight center triangles is a corner of the cube.


a.k.a. Jewel Puzzler, Christoph's Magic Jewel, Christoph Bandelow's Jewel
Left made in Taiwan circa 1990, right made by Mefferts 2010.
(left: plastic, 2 inches between square faces, opposite colors are
magenta / yellow, green / white, orange / red, blue / gold;
right: 2.6" between square faces, all squares are brown, opposite colors are
yellow / light blue, red / orange, purple / pink, green / blue)
Like the Octahedron, but without tips (it has the same dimensions and appears to have the same origin of manufacture). A puzzle like this but with less interesting graphics was sold as Christoph's Magic Jewel, and more recently by Meffert's as Christoph Bandelow's Jewel.
Here views of the other 7 hexagonal faces:










Inventor Tony Fisher, purchased from Mefferts 2024.
(plastic, 3" between parallel faces)
In the theme of the Ghost Cube, it becomes very jumbled looking very quickly. The puzzle has click stops, where the solved position is not at a stop. So initially, the only move is to rotate to a stop, and then the puzzle can be mixed up bu moving from stop to stop along possible lines of rotation. The three photos above are solved, rotation to a click, one additional move to a click.
Patented by Erno Rubik, 1983.
(plastic, 2.5 inches diameter by 1.5 inches high;
yellow opposite green, blue opposite orange, grey opposite red;
also made in promotion versions and with six distinct pairings of the six colors;
originally packaged like a cheese, with directions on the package bottom)
A predecessor to the Rubik UFO where the two layers cannot rotate with respect to each other. Similar to a Puck Puzzle with fewer sections and without the center portion (but with the ability to flip along any of the three lines). Although this is not a trivial puzzle (harder than Rubik 1x2x2), it is not hard to solve by just playing with it. It can be solved to different color combinations (e.g., left below) and different patterns (e.g., the two on the right below). Jaap's Page presents a solution.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/kepkorong.htm
Rubik Patent, from: www.uspto.gov - patent no. 4,410,179


Distributed by Winning Moves, purchased 2005,2007.
(plastic, same puzzle with different colors, 3.25 inches)
The two types of moves that can be made are to twist by 180 degrees along one of the three axes (having the effect of exchanging three top segments with three bottom segments), and to rotate the top and bottom with respect to each other by multiples of 60 degrees. This mechanism can be viewed as a generalization of Rubik's Cheese where the ability to rotate has been added.
McFarren's Page presents a solution that first solves the top and then the bottom. Jaap's Page also presents this approach, as well as one that starts by pairing up top and bottom segments.
The opposite sides of both versions shown above are black (the green/black is translucent):


Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/rubufo.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/ufo/ufo1.htm
Rubiks.com booklet,, from: http://www.rubiks.com/World/Rubiks%20downloads.aspx


Made in China 2011.
(plastic, 2.7" diameter, 1.6" high;
blue top, green bottom,
purple opposite gray, yellow opposite white, orange oposite red)
Made in the theme of Rubik's Cheese but works the same as Rubik's UFO (the top and bottom layer can rotate with respect to each other). Here it is flipped over:

Made in China, 2012.
(plastic, 1.75" high by 1.75" diameter;
a 3-layer version of UFO Cheese)

a.k.a. Hockey Puck Puzzle
Patented by Z. Pataki, U. Mszmp, and . Csomos 1991, purchased from PuckPuzzles.com 2007.
(plastic, 2.9 inches diameter by 1 inch thick)
The outer ring can rotate around the center, and there is an axis along which two halves of the puzzle can be flipped with respect to each other. This puzzle is different, but in the theme of Rubik's Cheese Rubik's Cheese and Rubik's UFO Rubik's UFO. The puzzle can be easier depending on the graphics used; below are some other examples. Jaap's Page presents a general solution, and notes that this puzzle mechanism is virtually identical to the earlier Kep Korang puzzle.






Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/puck.htm
Smith Patent, from: www.uspto.gov - patent no. WO9,102,574

Purchased 2007.
(plastic, 4.1 inches diameter with 2.3 inch diameter center sphere)
Works the same as the Puck Puzzle but has fewer sections. Jaap's Page presents a solution and also discusses the relationship of this puzzle to the Brain Ball, Master Ball, and Top Spin.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/saturn.htm



a.k.a. Varia Disk
Patented by I. Perdy 1983.
(plastic, same puzzle with different colors, 4 inches)
The four pegs, each composed of four quadrants, can be rotated. In addition, the top and bottom halves can rotate with respect to each other, causing two quadrants of each of the four pegs to be moved to the next peg. The goal is to match each quadrant of each peg with the color on that position of the body. Each of the eight colors appears on two of the quadrants. For a harder puzzle, the two copies of each color are marked with one or two dots, and the puzzle can be solved by making the markings match as well (one dot goes to the left and two dots to the right). A newer version of this puzzle was sold as the Tricky Disky.
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/tricky.htm
Peredy WO Patent, from: www.epo.org - patent no. WO83/01009

a.k.a. Tricky Disk, Mind Trapper
Patented 1989.
(plastic, 2.4 inches diameter, 3.5 inches prong to prong)
This is a later version of the Hungarian UFO puzzle that was patented in 1983 (different cosmetically, but the same puzzle). The two copies of each color are distinguished by a small circle or triangle (instead of one or two dots as in the case of the Hungarian UFO), and these same markings are on each end of the color bars on the body.
Here is a simpler three-prong version and the directions that were sold with it:


Made in China, 2007, body is 2.2 inches diameter.
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/tricky.htm
International Patent, DE3,821,297.

a.k.a. Alpa-2-Go
Patented by D. Pop 1992, made by 2MUCHFUN, Bellevue, WA.
(plastic, 3 by 3 by 1.8 inches;
was also sold with a white body)
This puzzle was sold in a box where the front has a photo of the inventor and the back has a letter from the inventor and directions for use (an owners manual was also included).
Each of the four hexagons, formed from six triangles, can rotate; in addition, the upper and lower halves of the body can rotate (the puzzle works in a way similar to the Hungarian UFO and Tricky Disky, but has six triangles per hexagon rather than four quadrants per peg). When solved (as shown above), each hexagon face is one of the colors red, white, blue, or yellow, and when looking perpendicular to a face, you see the same color on the face, the top and bottom edges of the square, and the two diagonal edges of the two adjacent hexagons. This puzzle was also made with a white body and in promotional versions.
Jaap's Page presents a solution where, by reserving one hexagon for temporary use, one can solve the other three hexagons in six steps that consist of simple cycling triangles into the upper or lower half of a hexagon; then specific transformations are presented for fixing the final hexagon without disturbing the already solved three.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/alex.htm
Pop Patent, from: www.uspto.gov - patent no. 5,116,052

Netblock UFO,
Patented by K. Chan 1997,
purchased from Mefferts 2006.
(plastic, 3.5 inches)
Sando Ring,
Patented by Z. Pataki et. al. 1996.
(plastic, 5.5 inches)
Each of the three balls can rotate, and so can the halves of the balls. Also, the upper and lower halves of the puzzle can rotate with respect to each other (so it is possible to mix up the eight quadrants of the three balls with each other). This is a relatively easy puzzle where you can solve one ball at a time. Jaap's Page prersents a solution.
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/ufo.htm
Chan Patent, from: www.uspto.gov - patent no. 5,628,512
Pataki WO Patent, from: www.epo.org - patent no. WO96/08297

a.k.a. Meeting Colors, Disco Puzzle
Made in Indonesia and purchased in 2007.
(plastic, 5/8 diameter beads in 3.75 inch ring)
Eight beads each have 4 sections and can rotate. In addition, the upper and lower halves of the ring can rotate with respect to each other (so it is possible to mix up the 4 sections of the eight rings with each other). Similar to the Netblock UFO and Sando Rings puzzles, this is a relatively easy puzzle that can be solved one bead at a time. Jaap's Page notes that a similar puzzle is described in the patents of Ayers and presents a solution.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/octo.htm
Power Strike Page, from: http://www.powerstrike.net/puzzles/spotlight/octo.htm
Ayers Patent, from: www.uspto.gov - patent no. 4,708,345
Ayers Second Patent, from: www.uspto.gov - patent no. 4,881,738


Patented by Gerhard Huncaga 1994.
(plastic, 4.4 inches)
Each of the eight balls is split in half, and so is the main center white disk. By rotating the two halves of the disk with respect to each other, different halves of the balls can be matched up. As shipped from the factory, the blue center dial can be rotated to point the red dot to any ball, and pushing the white button in the middle of the dial causes that ball to be flipped. The puzzle can be solved one ball at a time:If necessary, use the button to make both halves of this ball you want to fix be on the top half of the disk. Rotate the bottom half counter clockwise from the position of one ball to the other. Flip that ball. Then rotate the bottom half clockwise to match the two halves. Since the bottom half was rotated the same amount in both directions, the previously solved balls remain solved, and so this procedure can be repeated to solved all the balls.In this basic factory configuration, this puzzle amounts to a simpler version of the Octo puzzle. However, the white cap of the button can be unscrewed to expose four rods with teeth that can be pulled out. In the factory setting shown on the right above, one rod (at the lower left) has been pulled out of its slot and pushed back in at the lower left corner, which causes the point of the dial that faces down to be active (rotate the ball a half turn first so after pushing in the rod it positions correctly). This can be done to any of the rods, allowing the push of the button to cause 1, 2 (at both 90 and 180 degree configurations), 3, or 4 balls at once to be flipped. The dot on each of the four points of the dial (on both sides) can be rotated between blue and red to remind you of which points are active. Do all of this with the puzzle in the solved state (since not all positions are reachable in other settings). Jaap's Page gives solutions for all other settings.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/gerdig.htm
Gerhard Patent, from: www.uspto.gov - patent no. 5,370,394





Patented by A. Unsicker 1999.
(plastic, 3.5 inches, the back side of each number is white)
Numbers are yellow on one side and white on the other, and can rotate any number of positions in either direction. In addition, there is a north pole that spans three numbers (13, 1, 2 in the photos above) and a south pole that spans four numbers (6, 7, 8, 9 in the photos above); a flip turns these 7 numbers along the pole axis:
->
Solution: Use ideas from Jaap's Page (which also presents moves to speed up solving). For a positive integer n, n and -n denote clockwise and counter-clockwise rotations by n positions, and / denotes a flip. The pole position P is the center of the north pole, and the two positions to its right clockwise are Q and R.
Step 1: Make the side facing you all yellow by using as needed:2/-2/2/-2 = flip the pole positionStep 2: From 1 to 11, move counter clockwise to its position, using:1/-1/6/-6/-6/-6/-1 = PQR -> RPQStep 3: If 12 and 13 are reversed, change parity by changing the side facing you from yellow to white (which mixes the numbers) turn over the puzzle, and repeat Steps 1 and 2:
That is, repeatedly move the next piece to position R and use this transformation to advance it two positions towards its goal. If it is only one position away, first advance number to its right./5/5/ = flip all of the numbersFurther reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/brain.htm
Unsicker Patent, from: www.uspto.gov - patent no. 6,003,868


K8 Ball
(plastic, 3.25 inches)
A Rubik's 2x2x2 with a smooth internal mechanism patented by S. Khoudary 2000. It has been made with different graphics besides the "K8" graphics shown on the two balls above; here is an example:


Ying-Yang Ball
(plastic, 3.25 inches;
on one section "K-Ball" is molded into the plastic near the point
and near the opposite side of that section,
"World Patents WO0025874 Made in China")
Further reading:
Khoudry International Patent, IP25874.


Works like a Rubik's 3x3x3.
(plastic, left 3 inches, right 3.5 inches)

Made in China, 2010.
(plastic, 2.8 inches wide, 3" high with stem)
Mechanically, the same puzzle as the standard Rubik 3x3x3, and any solution for that puzzle can be used, but here it is the shape that gets mixed up rather than the color.

a.k.a. Duo Master
Patented by Geza Gyovai 1989.
(3 inches)
The three basic moves are a north or south pole 45 degree turn, an equator 45 degree turn, or one of the four longitude 180 degree turns. Solve the rest of the puzzle first and then solve the poles by interleaving pole turns with pairs of longitude turns; or, solve the poles first and then as you do the rest maintain the poles solved (or in solved halves that can be fixed at the end). The NS pattern, where the top half is white and the bottom half black, is easy to visualize and not hard to do once you have worked with the puzzle a bit.
From NS, one longitude turn followed by one equator 180 degree turn gives EW:



From EW, the following sequence gives a rectangular checkerboard:



Or, the use four steps to get the "slice" pattern, and one more to get the "checkerboard":






Like the standard Master Ball, except with stars on one pole (has no significant effect on solving) and the letters U, S, A on three of the center white tiles. Two possible solutions are shown below. On the left is the slice pattern (the A is on the next white slice to the right of the S), on the right is the NS pattern, and in the middle is a pattern than can be used to go from the left to the right, as described below.



Solving the slice pattern with letters arranged:Solving the NS pattern with letters arranged, method 1:
- Ignore letters and solve checkerboard as for the standard ball.
- With the checkerboard pattern, longitude 180 degree turns and equator 90 degree turns preserve the checkerboard pattern; so it is easy to permute the center white tiles to put the U, S, and A tiles where ever you want.
- Do a 45 degree equator turn to restore slices, and fix the poles.
Solving the NS pattern with letters arranged, method 2:
- Starting with the slice pattern, rearrange the letters (using step 2 of the slice pattern solution above) to the position shown in the middle photo above.
- Reverse the NS to slice pattern transformation of the standard master ball by starting with the U to the left of the plane used for the first longitude turn.
NOTE: For a different transformation for slice to NS, the correct starting position can be determined by marking the center white tiles and seeing where they go when you do your transformation.
Once solving the standard and USA versions has been mastered, this is not too much harder. Again, poles can be solved separately. Then, one approach is to get the top and bottom halves to each have one of each color, and then use method 2 for the USA Masterball (which also has the effect of exchanging two bottom tiles) to make tiles to line up from top to bottom.Other Versions of Master Ball

a.k.a. Geo Master
The Master Ball has been made (with the identical size and mechanism) with many different graphics (Circus Master, Dragon Master, Soccer / Football Master, Tennis Master, Cat Master, WWF, etc.), including promotional versions (e.g. Paramount Pictures IQ), making the puzzle a bit harder than the rainbow version by making all sections unique. Jaap's Page presents a general solution.



Circus Master



Soccer Master
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/master.htm
Gyoval Patent, from: www.uspto.gov - patent no. 4,856,786


a.k.a. Creative Puzzle Ball
Patented by U. Meffert 1994; purchased from Mefferts.com 2005.
(plastic, 3 inches, keychain is 1.5 inches)
This puzzle rotates about the center along 4 different planes that partition the surface into 8 triangles and six squares. Rotation has click stops but is not symmetric in that if you split a ring in half by turning half the puzzle 180 degrees, you don't end up in a click stop. Internally, it uses a mechanism equivalent to the skewb cube. Here's what Meffert's says about the puzzle:
"The 3-D Puzzle Ball moves a group of three squares and four triangles through 120 degrees by rotating around the triangle at the center of the group. It has precision injection moulded parts with spring-loaded bearings which make operation easy and exact; this is a puzzle which definitely won't fall apart in your hands. The idea of the puzzle is to scramble the colors and then return them to the initial state. You may also want to make pretty patterns with it as well though. The Beach Ball Puzzle is difficult enough to be a real challenge, but easy enough to master, without help, in a few days. Just in case you do have difficulty in solving the Puzzle, a solution booklet is included with the puzzle."
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/beachbll.htm
Meffert's Page, from: http://www.mefferts.com/puzzles/creasol.html
Meffert Patent, from www.uspto.gov - patent no. 4,474,376

a.k.a. Incrediball
Patented in 1984 by William O. Gustafson and others;
purchased from Mefferts.com.
(3 inches)
Each of the groups of five triangles can rotate (it doesn't look like they should be able to, but there is a spring mechanism that lets them flex up enough to rotate). The groups intersect in twelve circles. In the solved state, there are six distinct circle colors, where each circle has the same color as the one opposite it. Jaap's Page notes that this is the same puzzle as the Kilominx, and presents a solution.
Further reading:
Meffert's Page, from: http://www.mefferts.com/puzzles/impossol.html
Jaap's Page, from: http://www.jaapsch.net/puzzles
Gustafson Patent, from www.uspto.gov - patent no. 4,474,376)
Blazek and Jandora Patent, from www.uspto.gov - patent no. 6,994,343)
Djukic DE Patent, from: www.epo.org - patent no. DE20211793
Djukic WO Patent, from: www.epo.org - patent no. WO03105978
Obermair DE Patent, from: www.epo.org - patent no. DE3204033


Patented by Zoltan and Robert Vecsei 1993, purchased from Mefferts 2007.
(plastic, 3.5 inches)
This puzzle has twenty faces that meet at 12 vertices. Mefferts has made this puzzle in a number of color schemes, including the 12 color "Dogic 1" (on the left above) where each vertex is colored, the 10 color "Dogic 2" (on the right above), where each face is colored (and each color appears on two of the 20 faces), the 5 color "Dogic 3", the 2 color "Dogic 4" and "Dogic 5", and the 20 color "Dogic 6". A set of 5 faces can be rotated about a vertex, or just the five triangles that meet at a vertex can be rotated.
Here are what a few moves of Dogic 1 look like:




Here are what a few moves of Dogic 2 look like:




Jaap's Page gives a solution that solves one tip at a time, and then uses the solution for the Impossiball to solve the faces.
Further Reading
Meffert's Page, from: http://www.mefferts.com/solution/dogic/dogic_solution.htm
Jaap's Page, from: http://www.jaapsch.net/puzzles/dogic.htm
Vecsei HU Patent, from: www.epo.org - patent no. HU214709


a.k.a. Eight Planets Bermuda Cube
Purchased from MF8 China, 2012.
(plastic, 2.1" square base, 2.5" floor to peak)
A Rubik 3x3x3 in a house shape, constrained in two different ways, the "Red Roof" and "Green Roof" versions:








Designed by Li Chung Man, sold by SMAZ, 2012.
(plastic, 2.6" face to face;
yellow opposite white, blue opposite green, red opposite orange)
This puzzle works like a Rubik's 2x2x2 puzzle with the addition of a wheel of 12 numbers on each face. It can also be viewed as a generalization of the Smart Alex and the Hungarian UFO / Tricky Disky puzzles.

a.k.a. Magic Octagonal Prism, The Octagon, The Barrel
P.G. CO, circa 1980's.
(left plastic 2.2 inches, right metal ring and plastic 1.25 inches)
This is the same as Rubik's 3x3x3 Cube with the corners beveled along the vertical dimension, and the same solution can be used. However, as shown below, it can look like a bit of a mess and, as explained on Jaap's Page, Jaap's Page, you may have to flip a single edge by flipping it and a beveled one, or exchange two pieces by exchanging them and also a pair of beveled ones.

Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/barrel.htm

Same puzzle as the standard 3x3x3 Rubik's Cube.
(plastic, 2.2 inches)
This puzzle is shaped like the Rainbow Cube (a cube with the corners cut off); there are six square faces corresponding to the faces of a cube (colored green, blue, light blue, orange, yellow, and white) and eight triangular faces corresponding to the corners of a cube (colored red, green, gold, purple, grape, pink, white, and cream). However, the operation of this puzzle is different. Here, a layer parallel to a square face can rotate, and a solution for a standard Rubik's 3x3x3 Cube can be used.
Further Reading
Wikipedia Cuboctahedron Page, from: http://en.wikipedia.org/wiki/Cuboctahedron

Purchased from PUZL.co.uk 2007.
(plastic, 2.25 inches)
This puzzle is shaped like the Cuboctahedron (a cube with the corners cut off); there are six square faces corresponding to the faces of a cube (opposite pairs are colored red, yellow, and orange) and eight triangular faces corresponding to the corners of a cube (opposite pairs are colored green, blue, light blue, and purple). However, the operation of this puzzle is different. Here, triangular faces (formed from 4 little triangles) can be rotated.
Jaap's Page gives a solution, notes that this puzzle has eight axes of rotation like the Skewb, and discusses the relationship of this puzzle to the Dino Cube, Brain Twist, and Platypus.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles

Designed by Tim Selkirk, sold by Mefferts, 2012.
(plastic, 3.25" x 3.75" x 2.3")
Works like a Square 1 puzzle with different restricted movement:
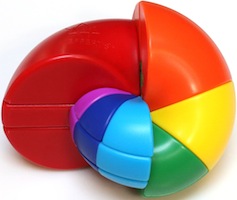





Sold by Mefferts, 2013.
(plastic, 2.5" high by 3" wide from point to face)
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/pentahed.htm





Sold by Mefferts, 2013.
(plastic, 2.5" high by 3" wide from point to face)







Sold by Mefferts, 2013.
(plastic, 2.5" high by 3" wide from point to face)
Like other "crazy" cubes such as the Crazy Cube 3x3x3, faces either spin around a circle or the circle spins with it, depending of which version of the 8 versions named after the planets is purchased; this one is the "Mercury Version".






Sold by Mefferts, 2013.
(plastic, 2.5" high by 3" wide from point to face)

Made in Hungary, circa 1980's?
(plastic, 2.25 inches across minimum dimension, 3.5 inches across farthest points;
white body with colors red, light blue, dark blue, green, yellow, brown, gray, black;
the same puzzle was also made with different color schemes,
including orange, yellow, red, blue, and green bodies)
Each of the six points can rotate, and the object is to make a circle of the same color on each of the six faces on which the points sit.
This puzzle is commonly referred to as the "Dino Star" because it is logically the same puzzle as the Dino Cube. Each of the six points corresponds to a corner of the Dino Cube. When a point rotates, 3 pairs of colors move. For example, looking at the photo above, when rotating the forward facing point, the circle of red rotates, and as it does, the red and blue segments rotate together (as do the other two red segments with the two other colors that cannot be seen in the photo). These pairs of colors that move together correspond to the pairs of triangles that move together on the Dino Cube (a total of 12 pairs in either puzzle). To color the Dino Cube to be like the Dino Star, start with a blank cube and draw a circle of a unique color around each corner; the result will be each triangle pair having two different colored arcs on it:
->

a.k.a. Other Name
Patented by Adam Alexander 1985, made by Ideal Toy Co. 1992.
(plastic, 3.5 inches)
Each point can be rotated around the plane perpendicular to it. The solved state, as shown in the photo above, is when each pair of parallel planes is the same color. Jaap's Page mentions the relationship of this puzzle to the Megaminx and presents a three step solution, where the first step uses only two simple trnsformations to solve everything except the five pieces around one vertex, the second step positions the edges of this final vertex using one of five transformations, and the final step employs two transformations to orient these edges.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/alexandr.htm
Alexander Patent, from: www.uspto.gov - patent no. 4,506,891
Nieto Patent, from: www.uspto.gov - patent no. 4,500,090


a.k.a. Jackpot
Patented by Seyhan 2006, purchased from Mefferts 2007.
(plastic, 4.5 inches;
both have tips A, K, Q, J and faces clubs, diamonds, hearts, spades;
a "collectors" version on right has faces colored green, yellow, red, blue)
Both the tips and faces can be rotated:



Jaap's Page presents a solution and relates it to that for the Dino Cube, Rainbow Cube, and Brain Twist. Mefferts has made a number of versions of this puzzle and gives four challenges for the Jackpot version that is shown on the right above:1. Match all four card suites on each side.Mefferts has sold other "collectors" versions, and also versions with electronics where lights go on when a side is solved.
2. Match the same 3 outside card suites to different card suite centers.
3. Line up all the J (Jacks) Q (Queens) K (Kings) and A (Aces) on each of the 4 apex columns.
4. Line up the matching color bars in 6 locations around the center core.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/dinocube.htm
Mefferts's Page, from: http://www.mefferts.com/solution/jackpot/index.html
Seyhan International Patent,, WO03/004117.


a.k.a. Golden Egg, Silver Egg, etc.
Designed by Tony Fisher, purchased from Meffert's, 2009.
(plastic with metallic finish, 4.25 inches high by 3 inches diameter;
left "Golden Egg", middle "Golden and Silver Egg", right "Silver Egg";
also made in gold+silver, copper, white, red, green, blue, and yellow)
Like the Golden Cube, uses a Skewb mechanism and has a shiny metallic finish, and in the same spirit as the Rubik 3x3x3 Mirror Block pieces of the cube are distinguished by shape rather than color. In fact, the shiny surface combined with the egg shape make this puzzle almost like a fish eye lens when photographed (one can see the photographer and much of his kitchen in the photos above).



Patented by C. Hoberman and M. Davis 2005, made by Hoberman Designs.
(plastic, each edge of the pyramid shape is 4.75 inches)
Below are the directions that came with the puzzle. Jaap's Page presents a solution and relates it to that for the Dino Cube, Rainbow Cube, Platpus.

Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/dinocube.htms
Hoberman and Davis Patent,, from: www.uspto.gov - patent no. 7,125,015


Patented by F. Gruber 1993, Copyright Interconcept GmbH.
(left: plastic, 3 inches, 3-wing version, red / blue / yellow;
right: plastic, 4-wing version, black / white / blue / green / red / yellow / gray / purple)
The basic operation is to make two of the semi-circles co-planar and then rotate the resulting circle 90 degrees. After mixing up, restore the puzzle to a fun pattern. Below are the directions that were sold with the 3-wing version. Jaap's Page presents a solution.




Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/roundy.htm
Gruber Patent, from: www.uspto.gov - patent no. 5,267,731

There are many puzzles that are not of the same general form as Rubik's Cube, but are in the same theme of a manipulation puzzle (often quite hard) that you can pick up, play with, and put down unsolved without being stuck with a bag of pieces.


a.k.a. Rubik's Magic Junior
Wallace and Gromit, made by A. R. Mason, U. K. 2007.
(plastic, four 2" panels held by wire loops, when front is solved, back is not)
The smallest of the Rubik magic panels puzzles. There are four ways to fold the puzzle in half; as shown in the directions to the Rubiks Magic Junior Picture Game series (see the next page), two of these let you do the loop transform (also called the roll) and two the star transform. By learning what they do, the puzzle can be solved very quickly, or by just more or less randomly playing with them, the puzzle usually solves without too much effort.
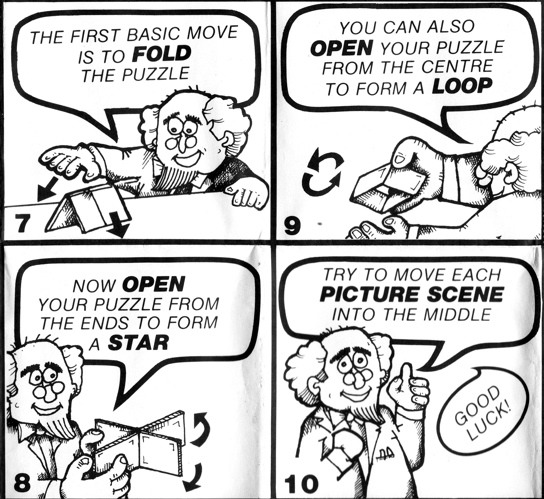
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/magicmini.htm#desc
This series of four puzzles, made by matchbox 1986 (plastic, four 2" panels), each has mice, so that the four can make a larger scene of mice. The opposite sides with backgrounds of yellow, brown, green, and blue, have cute characters that can be arranged in a number of ways.










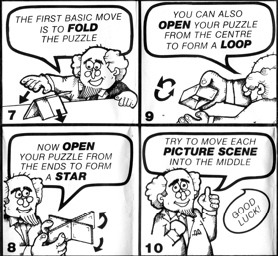



Rubik Studio Promotional Mice Theme 1985 (Hungarian).
(plastic, 2" panels, both sides always look solved;
shown is the position when the text runs along the bottom)


Rubik Studio Promotional Fantasy Theme 1988 (Hungarian).
(plastic, 2" panels, when front is solved, so is back)


Kellogg Promotional 1988.
(plastic, 2" panels, the little top center left triangle on the front side has been repaired,
"RUBIK/RUBIK'S MAGIC TM PROP OF 7 TOWNS LTD PATENT APPLIED FOR
C 1988 KELLOGG COMPANY MADE IN CHINA")


Hungarian Malev Airlines promotional 1989, Buda Castle on the back.
(plastic, 1.5" panels, front and back not solved at the same time)


Hungarian Malev Airlines promotional 1989.
(plastic, 1.5" panels, when front is solved, back is not)


Hungarian Apisz Promotional 1986 (paper and accessories store).
(plastic, 2" panels, when front is solved, so is back)


Scooby Doo, www.rubiks.com, circa 2000.
(plastic, 2" panels, when front is solved, back is not)


Simpsons, made by A. R. Mason, U. K. 2007.
(plastic, 2" panels, when front is solved, back is not)


England tourism promotional, made in the U.K 2007.
(plastic, 2" panels, when front is solved, back is not)




Patented by E. Rubik 1987-U.S. & 1985-Hungary.
(plastic, eight 2" panels, original black panels and newer red panels)
Eight panels, held by wire loops, can be folded and manipulated. Mix up and restore the 2x4 solution of 3 rings, or make the reverse side 3x3 (with a missing panel) solution of 3 linked rings. It is also fun to make different 3D shapes.
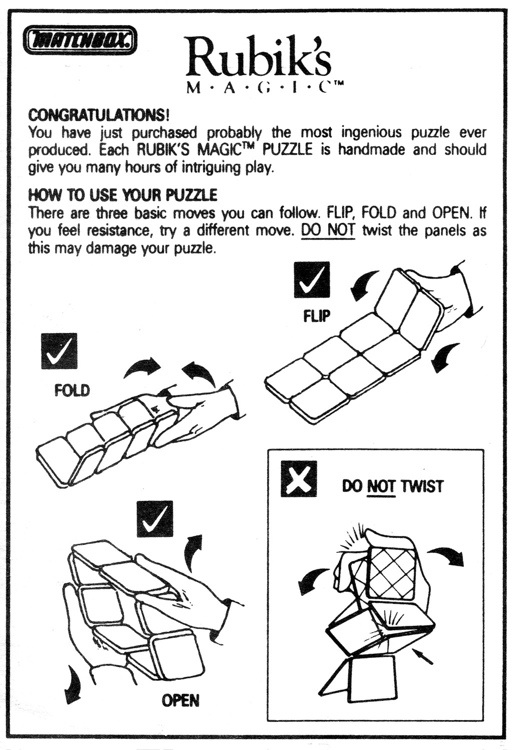
The star transform of Rubik's Magic Junior can be generalized, the Rubik's Magic directions show a generalized loop (called roll) and three new ones:
star transform:
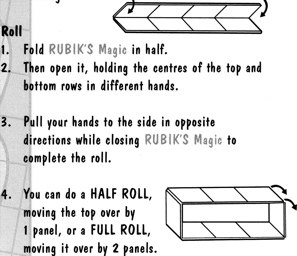
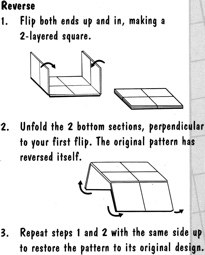
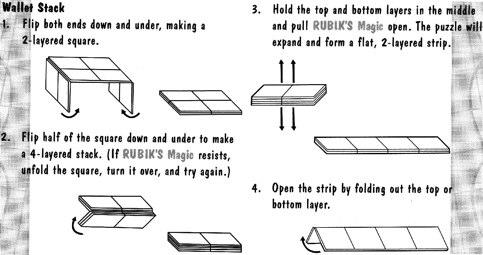
Note: If in Step 3 of the wallet stack
you pull it apart horizontally
instead of vertically, you get the
"row swap transform"
(see Jaap's Page) that exchanges
the top and bottom rows.
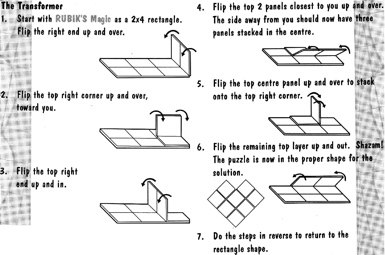
After mixing up the puzzle, simply playing with the basic transformations typically gets you back to the starting pattern of three disconnected loops, and the more you do it, the more you get an intuition on how to do it faster. At some point, it is useful to really think about what each transformation does. Below, on the left is shown the starting position with panels labeled from 1 to 8 (or the back of the starting position with panels labeled A through H). The right shows where each panel goes; bars indicate where the top of that panel is now positioned.
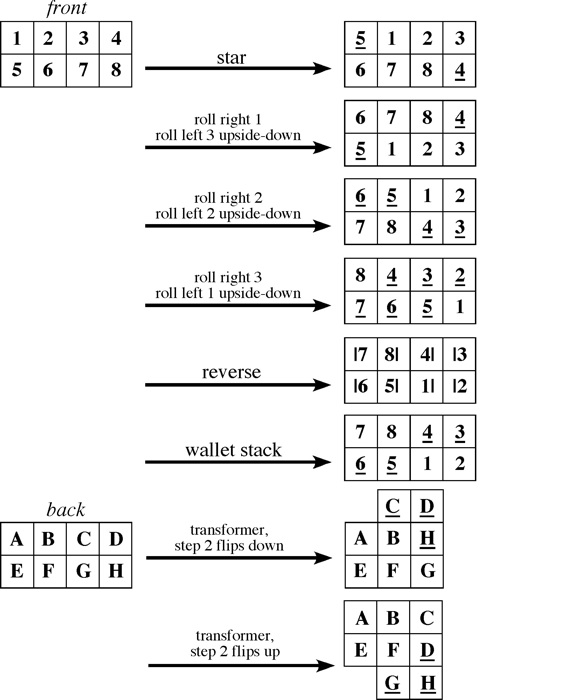

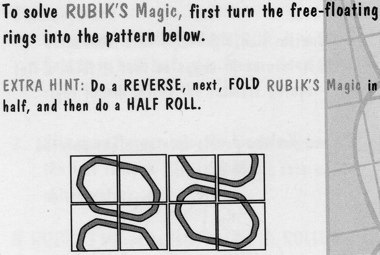
The basic transformations together with the two hints of the red panels directions shown above lead to the following solution. Some other versions of the puzzle (e.g. Simpson's and Harry Potter) have the graphics placed so that this solution works.
0. If necessary, as per Hint 1, play with transformations to restore the 2x4 solution; if using the new red version, reposition it with the copyright at the top (text upside-down).
1. As per Hint 2, do a reverse, and then position the puzzle horizontally (where the upper right three panels are are the lower right three panels of the linked solution):

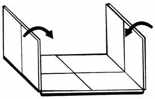
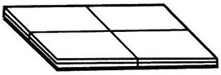
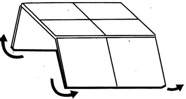

2. Continuing as per Hint 2, do a half roll towards the left that moves the upper right three panels to the lower left (when you are done, the underside has the pattern shown in Hint 2):

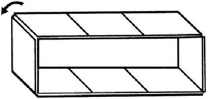


3. Do the transformer:
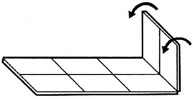
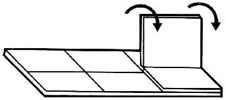
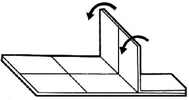

Jaap's Page credits the following method to Alexander Oohms.
0. If necessary, play with the transformations shown in the puzzle directions to restore the puzzle to the 2x4 solution.
1. Fold the right two panels up and then fold lengthwise:




2. Arrange into a 2x1 box where the right side is two panels thick, fold the extra two panels up through the box and back down (so they are now on the outside right), and then push the right side in to make a stack of 6 panels:




3. Push the stack of 6 down so that you have an open half box with a bottom that is 2 panels thick, flip the extra 2 panels under the bottom around 180 degrees to lie flat, and then rearrange into a Z shape:





4. Flip down the extra two panels on the back of the top of the Z (so the center of the bottom row is now three panels thick), flip the third center panel to the left so that all three sections of the bottom row are now two thick, then flip the extra row of three on the bottom down:






New orange version, 2" panels, same as new red one.


Simpsons, 2" panels.


Harry Potter, 2" panels.


Porsche / Mercedes, 1.5" panels.


Mini Dinosaurs, 13/16" panels (really small but it works).
Jaap's Intro, from: http://www.jaapsch.net/puzzles/magic.htm
Jaap's Transforms, from: http://www.jaapsch.net/puzzles/magictrn.htm
Jaap's Solutions, from: http://www.jaapsch.net/puzzles/magicstd.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/rm1/rm1int.htm
Koller's Page, from: http://www.mathematische-basteleien.de/magics.htm
Garron's Page, from: http://cube.garron.us/magic.htm
Rubiks.com booklet, from: http://www.rubiks.com/World/Rubiks%20downloads.aspx
Rubik Patent,, from: www.uspto.gov - patent no.4,685,680


Same mechanism as the standard Rubik's magic panels.
(plastic, eight 2" panels)
This puzzle works the same as the standard Rubik's Magic, and the same transformations can be used (star, roll, reverse, wallet stack, transformer, etc.). On the top side (shown above) all panels the same green, red, blue, yellow clockwise pattern. On the bottom side, all panels have the same 4 colors, but not all in the same order.
The goal is to make a cube sitting on a 2 panel base; this can be done with the standard Rubik's magic as well, but here the graphics allow for two nice looking solutions with matching colors at the corners. The "horizontal" solution shown above has the text horizontally on the side and the "vertical" solution used to illustrate the solution steps on the next page has the text going vertically on the side.
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/magiccrea.htm#desc
We illustrate one of the solutions presented on Jaap's Page that makes use of a box and lid construction in the flavor of Ooms method for the standard Rubik's Magic solution.
0. With the bottom side facing up, manipulate the puzzle using the standard transformations to have the arrangement on the left (which leads to the horizontal solution) or the arrangement on the right which leads to the vertical solution (which we use for the illustrations below). One can go between these two arrangements with a standard right roll transform.


1. Flip the left two panels up an over, fold lengthwise, arrange into a box, fold the extra two panels on the right up and down into the box so now they are in the inside of the right:





2. Rearrange to three long with a stack of 4 on the right, fold the back right panel left to the middle, and fold up the front three:




3. Hold the left two panels with your left hand (don't let go until this step is completed), pull up the middle pair of panels up with your right hand to make a box, flex the left two panels to fold together towards you and use your right hand to guide the formation of the box, then unfold the two panels still in your left hand to make the base for the cube:





Left top original made by Matchbox 1987, left bottom newer black version.




(plastic, twelve 2" panels)
This puzzle works the same as the standard Rubik's Magic, and the same transformations can be used (star, roll, reverse, wallet stack, transformer, etc.). The goal generalizes the standard Rubik's Magic Panels to make a W shape on the back with the 5 rings unlinked. The puzzle directions also show many 2D shapes that can be made:

Further reading:
Jaap's Intro, from: http://www.jaapsch.net/puzzles/magic.htm
Jaap's Transforms, from: http://www.jaapsch.net/puzzles/magictrn.htm
Jaap's Solutions, from: http://www.jaapsch.net/puzzles/magicmast.htm#desc
Jaap's Page credits the following solution to C. McFarren, which reduces the solution to two applications of the standard Rubik's Magic transformer transform. The illustration below is for the original silver version; the newer black version also shown shown on the previous page works exactly the same (although Jaap's page notes that some of these puzzles have graphics placed in a way that a mirror image solution us used).
0. Do a roll to the right:




1. Flip the left and right two panels up an over, flip the upper left and upper right top panels towards you, fold the left two and the right two up and over towards the center to form an upside-down T, then fold the bottom upper two up and back to length the stem of the T:




2. Roll the base of the T one panel to the right and then fold out the bottom 4 from underneath to form a reverse L shape:



3. Do the standard Rubik's Magic transformer transform on the top of the L (note that for the second step, the panel flips to the left):






4. Do the standard Rubik's Magic transformer transform on the leg of the L (note that for the second step, the panel flips upward):









Left made by V.V.V. Puzzle 1987, right made by CN Studio and purchased 2007.
(plastic, twelve 2" panels)
Twelve panels, held by wire loops (length and confoguration differs from Master Magic), can be folded and manipulated. To change the back side to a cross:
0. If necessary, use basic transformations (as for Master Magic) to restore the 2x6 solution. For the black version, turn puzzle over (V.V.V at the top, upside-down).
1. Fold the top half down, rotate right two panels, and unfold:



 Note: For the black puzzle, you instead roll to the left, to end up with:2. Fold each end over, fold at the middle, split each side and fold together, fold the two 2x2 sections down, and then unfold the left and right portions of the cross:
Note: For the black puzzle, you instead roll to the left, to end up with:2. Fold each end over, fold at the middle, split each side and fold together, fold the two 2x2 sections down, and then unfold the left and right portions of the cross:





3. It is now solved on the other side (for the black, you don't need to turn it over).
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/magicrings.htm#desc




Upper left is the "standard version", upper right has different background color,
bottom two have 4 chess square per tile, all purchased in 2005.
(plastic, sixteen 2" panels)
This puzzle works the same as the standard Rubik's Magic Panels, and the same basic transformations can be used (star, roll, reverse, wallet stack, transformer, etc.) to make many different 2D and 3D shapes. Jaap's Page shows how to solve the back to a big W shape with five balls on it. It can easily be made into 4x4 panels; for the chess versions that have 4 chess squares per panel, it can be a fun challenge to rearrange the 2x8 shape, and then see what chess position results on the (front or back) of the 4x4 shape.
Further reading:Jaap's Intro, from: http://www.jaapsch.net/puzzles/magic.htm
Jaap's Transforms, from: http://www.jaapsch.net/puzzles/magictrn.htm
Jaap's Solutions, from: http://www.jaapsch.net/puzzles/magicsuper.htm#desc
Twisty Puzzles build info, from: http://twistypuzzles.com/articles/magic-super-master.shtml








a.k.a. Genius Puzzle
(3 section, 6 column tower is 1.75" by 2.75" long with 5/8" tiles,
3 section, 6 column Genius tower is 1.75" by 2.8" long with 5/8" tiles,
3 section, 6 column keychain tower is 1.75" by 2.75" long with 3/4" tiles,
3 section, 6 column McDonalds tower is 1.875" by 3.125" long with 1" tiles,
2 section, 6 column custom made tower is 1.75 inches by 2" long with 3/4" tiles
4 section, 6 column keychain tower is 1.25" by 3" long with 1/2" x 3/8" tiles,
4 section, 6 column keychain tower 2 is 1.25" by 2.25" long with 3/8" tiles,
6 section, 6 column tower is 2" by 4.75" long with 3/4" tiles)
A number of sections that can rotate; solved when each column has a single color. One color has one fewer tiles than the others, and this gap is what allows pieces to be moved around. Because all tiles of a given color are identical, solving is relatively easy; any tile can effectively be moved to any position without disturbing the others, with any assignment of colors to columns, one tile at a time (larger versions just take longer). When the number of number of sections and columns is the same, a second problem is to put the same color tile in each row.
When the number of number of rows and columns is the same, a second problem is to put the same color tile in each row.
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/tower.htm


Circa 1980's except the custom 2 section version purchased 2014.
(4 section, 4 column tower is 1.4" x 3.5" with 5/8" diameter balls,
4 section, 4 column key ring tower is 5/8" x 1.75" long with 3/16" diameter balls,
2 section, 5 column tower custom made in Ukraine is 1.5" x 2.25" with 5/8" diameter balls,
5 section, 5 column tower is 1.6" x 4" with 5/8" diameter balls,
7 section, 7 column tower is 1.6" x 4" with 3/8" diameter balls)
This puzzle is slightly different from the Whip-It Towers in that instead of one column missing a ball to create the gap, there is an extra section that has the gap. However, just like the Whip-It towers, any ball can effectively be moved to any position without disturbing the others (given that all balls of a given color are equivalent), and these puzzles can be solved in any order (with any assignment of colors to columns) one ball at a time (it just takes longer when there are more columns and / or sections). In fact, if you first just park one of the balls in the gap, then this puzzle is identical to the Whip-It Towers, except at the end you just drop the ball on on the appropriate column.
Because the number of rows and columns is the same (except for the custom made 2 section version), a second problem is to put the same color ball in each row.
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/tower.htm
The Smaries tower is identical to the standard 4 section Varikon tower except for color and the addition of the text at the bottom "Smarties Smarties Smarties Only Smarties Have The Answer". It comes with directions that frame it as a game with a number of things to do.





Purchased 2008.
(material, 3.5 inches)
A slightly easier version of a Whip-It Tower puzzle, where pairs of columns have the same color. Here is a photo fo the other side:




a.k.a. Ivory Tower
Patented in 1982 "Arxon Speil + Freizeit GMBH", made by Ideal Toy Co.;
Jaap's Page credits design to Endre Pap, who designed the Hungarian Rings.
left: 5 sections, 6 cols., 1.9" base, 1.6" top, 3" long, 7/16" dia. balls;
middle: 6 sections, 6 cols., 1.9", 1.6", 3.5" long, 7/16" dia. balls;
middle: 7 sections, 6 cols., 1.9" base, 1.6" top, 3.9" long, 7/16" dia. balls
Go from darkest to lightest color type in each column (red, blue, green, yellow, brown, gray). Different from Whip-It Towers and Varikon Towers; instead of a gap, there is a spring between two of the bottom balls that allows one to be pushed in so that the ball above it can drop down. This solution based on Jaap's Page:Further reading:
- Make each column have the same color type: Push one ball in to create a gap and then proceed as for Whip-It Towers and Verikon Towers (i.e., when all shades of a given color are equivalent, you can essentially use the gap to move any piece where you want to).
- Place all but the top two balls of each column: If XYZ are three consecutive balls in a given column, by making a gap in a column next to it, you can do XYZ -> YZX -> ZXY, and thus X can be moved down 2 sections, or Y can be moved down one section. With this trick, all columns can be ordered correctly except possibly for the top two sections.
- Fix parity if necessary: If an odd number of columns have the top two balls out of order, then rotate the top layer one position and repeat Step 1 on the top two layers only (so that the top two layers have the same color type as the already solved lower layers).
- Work two columns at a time to fix the top two layers: Pairs of columns that have the top two balls out of order can be fixed with the following nine step transformation that manipulates 6 balls; the top two balls and the gap are denoted A, B, #, and the balls initially below these three positions are denoted X, Y, Z. In this figure, columns are shown next to each other, but they can be anywhere, and the top two layers are always shown rotated so that the 6 balls being manipulated are together:
Step 1
AB#
XYZStep 2
ABX
#YZStep 3
A#X
BYZStep 4
AYX
B#ZStep 5
AY#
BXZStep 6
AYB
#XZStep 7
#YB
AXZStep 8
XYB
A#ZStep 9
XY#
ABZ
Babylon Towers Directions.
Jaap's Page, from: http://www.jaapsch.net/puzzles/ivory.htm
Babylon Towers DE Patent, from: www.epo.org - patent no. DE3104021

Circa 1990?
(plastic, 2.75 inches across by 3.5 inches high inches)
The numbers 1 to 31 are arranged in 7 columns of colored tiles (6 red, 6 yellow, 6 purple, 6 green, 6 orange, 6 blue, and 5 white), and the goal is to put the days of the month in increasing order going clockwise and down. Similar to the Babylon Towers, and a similar solution can be used, although this puzzle is easier because there are two blank tiles at the bottom of the green, orange, and blue columns.

a.k.a. Clever Toys Tower
Purchased by J. A. Storer in Bangkok 2008, this puzzle also sold by Clever Toys.
(wood, 2.9"x4.1", five each red, blue, green, and yellow 9/16 inch diameter balls)
There are four columns, which when solved, each have 5 balls of the same color. The ends cannot rotate; one has a single receptacle that can hold one ball and the other has one receptacle for each column. Harder than the Varikon Towers, but easier than the Babylon Towers.
Solution: It is convenient to think of the bottom as the end with the single receptacle and the top as the one with four receptacles, and to work from the bottom up in three steps:1. It is easy to place the bottom balls (it doesn't matter how you mix up the remainder of the puzzle).
2. The second and third rows can be fixed in a manner similar to the Varikon Towers (they are adjacent to the center by which the rings rotate).
3. The top two rows are adjacent to the top edge of the center ring and can also be solved in a manner similar to the Varikon Towers.

Made in Hungary circa 1980's?
(plastic, 2.2 inches diameter by 2.9 inches long inches)
Tiles are numbered 1 through 6 in red, 7 through 12 in yellow, 13 through 18 in blue, and 19 through 23 in green. Tiles can rotate around the barrel in each of the three loops. Tiles can also move between loops in two positions (in the photo above, between positions 4 and 12 and between 16 and empty position 24). The numbers can easily be arranged in any order in a spirit similar to but even easier than the Fifteen puzzle.



Patented in 1981 by S. Hanson and J. Breslow.
(plastic, 1.5 inches square by 5 inches long;
deluxe version has same size / end labels / directions, and
although photos do not show it well, it has chrome rings on all sides;
keychain version is plastic 5/8 inches square by 2.25 inches long)
A piece can slide into the empty slot and the puzzle can twist at the end sections, but not the middle. It is easy to solve the yellow and green columns (or any two of the non-white colors), and then the red and white can be solved without disrupting the already solved columns, where the basic operations are cycling 5 pieces (all but the top of one column and the bottom of the other or vice-versa), or cycling 3 pieces at one end of the puzzle or the other.
This puzzle is harder than a 4-high Whip-It Tower because you can't rotate at the center (solving the last two columns by cycling pieces is more like a 3D version of the Fifteen puzzle).
Below are the instructions that came with it:

Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/missing.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/rdml/rubmlk0.htm
Below are the other two sides and end stickers of the Missing Link and Missing Link Deluxe, and the other two sides of the Missing Link keychain (the keychain does not have stickers):





There are other productions of this puzzle; some the same but with different stickers (e.g., one sold in France said "Le Chainon Manquant" on the stickers), as well as ones that have the same dimensions but different colors, different internal construction, or different overall quality. Here are three examples of different ones with English language stickers; for all three, the stickers on the two ends are the same:










Made by Mariusz Dabrowski, 2007.
(plastic, 1.5" square, 3.8" long)
Custom made by replacing the double center portion of a standard Missing Link puzzle by a single section. This makes a puzzle equivalent to the (much easier) 3-Section Whip-It Tower.
Has solid ends with no holes or exposed parts (so stickers are not required on the ends to cover anything up) and a very smooth click-stop action. Here are the other two sides:


Made by Mariusz Dabrowski, 2007.
(plastic, 1.5" square, 6.1" long)
Custom made by extending the center portion of a standard Missing Link puzzle from two to three sections (using parts from two puzzles) in such a way that these three sections cannot rotate with respect to each other (so like the standard Missing Link puzzle, only the two end sections of the puzzle can rotate). This extension does not change the basic complexity of the puzzle; it can be solved the same way as the standard version (and this remains true for an number of extensions of the middle).
This particular puzzle has solid ends with no holes or exposed parts (so stickers are not required on the ends to cover anything up) and a very smooth click-stop action. Here are what the other two sides and other end look like:


Made by J. A. Storer, 2007.
(plastic, 1.5" square, 7.1" long)
Custom made by adding a second double center portion to a standard Missing Link puzzle (using parts from three puzzles). Some 6-section Missing Link puzzles have been made where all four center sections are joined (so that the puzzle only rotates at the ends), but this is just a longer version of the Extended Missing Link puzzle (and is not any harder). This Doubled Missing Link puzzle can rotate in three places (the two ends and between the two double center portions), and so is a new puzzle that is a bit easier than the standard or extended versions, but still harder than the reduced version or a Whip-It Tower puzzle.
Here are what the other two sides and other end look like:

The central spindle may differ between different Missing Link puzzles. The most common version that was sold in the U.S. has a solid plastic center spindle with bumps on it; start by getting three of one of these:


After removing the stickers (save them), one end cap, call it the bottom, has a recessed hole in which sits a flat end of the spindle, and in the other end, call it the top, the spindle comes to a point and locks with two prongs into a smaller hole.
Take apart three Missing Link puzles. Force the top end off (ok if it breaks, it won't be used), slide off the sections, and slide the tiles out of the sections. All of the sections are identical; each has a locking side and free side (when two locking sides face each other, those two sections cannot spin with respect to each other).
Find a metal rod that has a diameter to match the holes in the sections, line up on the rod a bottom end, six sections, and a second bottom end, and mark where to cut so the length of the rod will be slightly shorter than the distance between the insides of the recessed holes of the end caps. Then drill and tap a 5/8 inch deep 6-32 threaded hole into each end of the rod (easiest to drill the holes on a lathe, and you can also use the lathe to face off the ends of the rods). The head of a 6-32 screw and a washer will fit in the recessed bottom end cap holes.
Screw one end cap on tight with a 1/2" 6-32 screw and washer. Add the 6 sections where the locking side of section 1 faces the cap, the locking sides of sections 2 and 3 face each other, the locking sides of sections 4 and 5 face each other, and the locking side of section 6 faces the other end cap. As you are adding caps, add tiles (you will have more of everything than you need except the center white tiles, so you can do some selecting for best fit, condition, and matching colors).
To attach the second end cap, start with a screw that is too long (e.g., 3/4 inch), screw it all the way in until it jams, and test how loose the puzzle fit is. Then repeatedly trim the screw a bit shorter and try again until the fit is just right. That is, because the rod is slightly shorter than the end to end distance, the fit is not determined by the length of the rod (another way to do this), but rather by how much the screw head / washer is protruding from the end of the rod when it is screwed in as far as it will go. The screws should jam in very tight so they will never move (but can still be removed in the future); can also add glue.
Finally place stickers on each end; you can glue them or use double sided tape.

Made by J. A. Storer, 2007.
(plastic, 1.5" square, 2.6" long)
Custom made by removing the center portion of a standard Missing Link puzzle. This makes a puzzle equivalent to the (much easier) 2-Section Whip-It Tower.
A fun to puzzle to make from left over parts from the construction of a puzzle such as the Doubled Missing Link, and could be made by using a new central spindle.
This particular puzzle made use of a version of the missing like puzzle in which the central spindle, rather than being solid and bumpy as is most common, is a smooth tube. The construction was very simple: Remove one sticker and end cap, take the puzzle apart, cut the spindle to just the right length, slide two sections onto the spindle with tiles placed appropriately, and screw the end cap back on with a 1" 6-32 screw. The screw has a loose fit in the tube but stays in place because it goes in an inch (and you can add glue if needed). The screw head and washer sit inside the recessed hole of the end cap, and the sticker is put back on to cover it up.
Here are the other two sides and the stickers on the ends:




Purchased on Amazon.com, 2013.
(plastic, 2.6" diameter)
Eleven balls protrude out of 12 holes (there is one empty hole at any time). A move consists of pushing in a ball that is adjacent to the hole to move from where it is into the hole position. Easy to solve; Jaap's Page presents a solution.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/index.htm


Hungarian Globe and Equator Ball, made circa 1982.
(metal covered plastic, 3 inches)

IQ Ball, circa 2000.
(plastic, 3 inches)
Three rings of 12 squares each (going around each of the three dimensions) can be rotated. The goal is to mix up the puzzle and then restore the original pattern, or in the case of the IQ Ball, the directions that were sold with it give different challenges. A number of 1980's and 1990's patents describe mechanisms for this puzzle, including the patent of R. Destics which describes a generalized mechanism (used by the Mozaika Puzzle) that can also twist along the equator, and the Magic Sphere puzzle allows faces to rotate. Jaap's Page presents a solution.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/equator.htm
Molnar GB Patent, from: www.epo.org - patent no. GB2088728
Green Patent, from: www.uspto.gov - patent no. 4,452,454
Green Second Patent, from: www.uspto.gov - patent no. 5,074,562
Liu Patent, from: www.uspto.gov - patent no. 5,114,148
Destics Patent, from: www.uspto.gov - patent no. 5,566,941
Maxim Patent, from: www.uspto.gov - patent no. 6,186,504



Made by Diff Design, Finland, purchased from Amazon.com 2011.
(plastic 2.75 inches diameter)
In a theme of the Hungarian Globe (a.k.a. Equator Ball), but with a gap into which pieces can move, mix up and then restore. This puzzle is the "Maailma" version; it was also made in a number of easier versions with simpler patterns; Jaap's Page presents solutions.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/index.htm

Patented by T. D. Chen 1998, copyright DaMert Co. 2005.
(plastic, 2.75 inches)
A generalization of the Hungarian Globe puzzle where six colored circular areas on the surface (red, orange, green, light green, blue, and purple) can rotate. This puzzle is all plastic with no stickers and works quite smoothly.
Further Reading
Chen Patent, from: www.uspto.gov - patent no. 5,816,571

K&T Toys,Inc., purchased 2007.
(plastic, 3.5 inches diameter by 6.5 inches long)
This is the "Limited Edition Patriotic Version"; this puzzle was also made with brown body. The directions give three increasingly hard challenges:1. Move the football from one side to the other.This puzzle can be solved in a fashion similar to the Fifteen puzzle (and a similar parity argument applies).
2. After mixing up the puzzle (e.g., after completing Challenge 1), return all the players to their respective sides (the end caps specify the red and blue sides of the puzzle).
3. Put the players into their correct sequentially numbered positions.

a.k.a. Wooden Screwball, Clever Toys Natural
Made by Clever Toys, 2008.
(wood, 3.5 inches diameter by 2.9 inches high)
This is a simpler version of the Rainbow Puzzle described on Jaap's Page, where the loops have only eight balls instead of ten (and the center ring moves only one row of balls) and when solved all balls in a loop have the same color.
Solution: Using two adjacent circles as scratch, it is easy to solve the other two. So without loss of generality assume that the puzzle is now solved except that in two adjacent circles, the red and black balls are mixed up. Rotate a black ball in the red circle to the center section, rotate the red ball in the black circle to one position away from the center section, spin the middle one position, rotate the black circle one unit, and spin the center section back. Keep repeating this step until solved. Note that this solution allows one to put the circles in any order.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/rainbowp.htm

a.k.a. Kaos
Patented by C. Hausammann 1993.
(plastic, 7 inches)
The top and bottom halves of these tubes can be rotated with respect to each other, and the balls can be shifted back and forth. Jaap's Page gives a solution. This puzzle was made in a number of versions that are the same except for the color of the balls and the packaging.




Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/chaos.htm
Hausammann Patent, from: www.uspto.gov - patent no. 5,176,382

Circa 1980's?
(plastic, 3.5 inches high by 2.75 inches diameter)
The top and bottom halves of the puzzle each have three tubes that can hold three balls each. By rotating the top and bottom halves with respect to each other, balls can be moved around to get to the solved state that has one empty tube and five tubes each containing three balls of the same color. This puzzle is in a similar theme to the Atomic Chaos puzzle, but easier to solve.

a.k.a. Stupid Cylinder
Czech Republic, circa 1990?
(plastic, 1.7 inches diameter by 2.7 inches long)
There are four columns such that when the puzzle is solved, each contains four tiles of the same color (red, green, blue, or yellow). The body can slide up and down and be used to rotate a row (which also rotates some blank tiles that are the same color as the body). The columns are not evenly spaced (two are adjacent and the other two are spaced apart from those and each other); below are some views of a solved puzzle. Jaap's Page gives a solution.



Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/pakovalec.htm


a.k.a. Billion Barrel, Tumbler Puzzle
Patented G. Yokoi 1983, made by Nitendo.
(plastic, 3.4 inches high by 2.8 inches diameter;
left 1980, green, blue, red, orange, yellow with black balls on green, yellow, red;
right 2009, orange, yellow green, blue, red with black balls on orange, red, green;
the Yoki patent also describes the Trillion puzzle) )
There are 23 balls in 5 columns, 4 of each of red, orange, yellow, green, blue, where three of the columns have an extra black ball. There are 6 rows of plastic rings around the puzzle where rows 1 and 6 cannot rotate, rows 2 and 3 rotate together, and rows 4 and 5 rotate together. The black body that holds the balls can slide up or down 1 unit inside the rings to shift the three longer columns. The goal is to put each of the 5 colors in their own column, with the three black balls on top of the three longer columns. Jaap's Page presents a solution. Here is a view of the other side of the solved puzzle, and a view of it mixed up:


Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/nintendo.htm
Martin's Page, from: http://www.smartbytes.co.uk/Tumbler/tumbler0.htm
Spanish Page, from: http://chelis.iespana.es/soto1.htm
Yokoi Patent, from: www.uspto.gov - patent no. 4,376,537


a.k.a. Russian UFO, Soviet UFO, Russian Flower, Festival Flower
Made in the Soviet Union circa 1980's
(plastic, 1.6 inch diameter disc, 2 inches across, 1+1/8 inches thick)
There are a total of 18 balls, 6 of each color. The discs on the top and bottom each hold 6 balls and rotate independently, there are six hidden positions in the middle layer and two extra holes on the side (a total of 20 holes). The puzzle can be manipulated to make different patterns, including one color hidden and the other two on each side.
Here is the green body version (shown above on the right) in its original packaging and the directions that came with it:





Made in the Soviet Union, 1985.
(plastic, 3" diameter by 1+1/8" thick, center is 1+5/8" diameter)
Same puzzle as the Russian Revolver of the previous page. Festival flower is the emblem of the World Festival of Youth and Students, and the puzzle was released in 1985 to the XII festival, which took place in Moscow. Here is the reverse side from the photo above:

Further Reading
World_Festival_of_Youth_and_Students Wikipedia Page, from: https://en.wikipedia.org/wiki/World_Festival_of_Youth_and_Students

a.k.a. Loophole
Patented by F. Lammertink 1992, copyright 1991 Binary Arts.
(plastic, 6 inches diameter by 1.25 inches thick)
Two discs that can rotate with respect to each other hold a total of 35 balls in six three ball slots on each side, at any time one slot is missing one ball, creating a gap into which a ball from that slot can be rolled or a ball from the other side can be pushed through if the discs are rotated appropriately. The slots on each side are arranged as three spokes and three outer slots; the three colors of the balls in the spokes are the same as the three colors of the outer slots on the opposite side. Jaap's Page observes that this puzzle is relatively easy to solve by first solving the inner two balls of each spoke and then the remaining balls, essentially correcting one ball at a time.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/backspin.htm
Lammertink Patent, from: www.uspto.gov - patent no. 5,172,912


Circa 1990's?
(plastic, 2.6 inches by 4.75 inches, left Pepsi graphics, right dinosaur graphics)
Plastic pieces slide on a diagonal grid in a generalization of the Fifteen puzzle. Here are views of the other sides:




Circa 1990's?
(plastic, 2.6 inches by 4.75 inches, left Coke graphics, right Sprite graphics)
Pieces can slide up and down and rows can rotate; a generalization of the Fifteen puzzle. Here are views of the other sides:



Copyright Winning Moves 2006, sold by Rubiks.com.
(plastic, 2.6 inches)
Twist the ring and pull to remove that triangle. Then slide the other triangles around to make different patterns. It is shipped in the pattern shown above with red on top, green on the bottom and a band of alternating blue and yellow around the middle.

a.k.a. Orb-It, l'ORBS
Patented by C. Wiggs and C. Taylor 1985, made by Parker Brothers.
(plastic, 3.5 inches)
When solved, the north pole ring has 8 yellow, the upper equator 20 green, the lower equator 20 red, and the south pole 8 blue beads. The puzzle can twist in 45 degree increments. The 45 (also -45, 135, and -135) degree rotations give one continuous loop along which all beads can rotate; fun, but the beads are hard to move this way, and it is not needed to solve the puzzle. A 90 (and -90) degree rotation creates two cycles of 28 beads that connect halves of the pole and equator rings. The 180 degree rotation joins opposite halves of the pole and equator rings.Based on the observation that incorrect beads always occur in multiples of 2, a simple solution, which is presented on Jaap's Page, works in three steps:

 1. Use 90 deg. twists to get yellow/blue to poles, green/red to equator.Steps 2 and 3 are easy; place one incorrect bead in each ring on opposite sides of the twist line, and then twist, rotate, twist, and repeat as needed. For step 1, a 90 degree twist followed by a rotation by one bead moves two beads from the poles to the equator and ice-versa. So first select an incorrect bead on each ring; if there are incorrect beads on only one pole or one equator ring, first use the ideas of Steps 2 and 3 to get at least one incorrect bead on each ring. Next, place the north pole incorrect bead next to the line on the left hemisphere, the upper equator incorrect bead next to the line on the right hemisphere, the lower equator incorrect bead next to the line in the rear on the right hemisphere, and the south pole incorrect bead next to the line in the rear on the left hemisphere. Then twist 90 degrees, rotate the vertical cycle counter clockwise one bead, and twist back. Repeat as needed.
1. Use 90 deg. twists to get yellow/blue to poles, green/red to equator.Steps 2 and 3 are easy; place one incorrect bead in each ring on opposite sides of the twist line, and then twist, rotate, twist, and repeat as needed. For step 1, a 90 degree twist followed by a rotation by one bead moves two beads from the poles to the equator and ice-versa. So first select an incorrect bead on each ring; if there are incorrect beads on only one pole or one equator ring, first use the ideas of Steps 2 and 3 to get at least one incorrect bead on each ring. Next, place the north pole incorrect bead next to the line on the left hemisphere, the upper equator incorrect bead next to the line on the right hemisphere, the lower equator incorrect bead next to the line in the rear on the right hemisphere, and the south pole incorrect bead next to the line in the rear on the left hemisphere. Then twist 90 degrees, rotate the vertical cycle counter clockwise one bead, and twist back. Repeat as needed.
2. Use 180 deg. twists to get north yellow, south blue.
3. Use 180 deg. twists to get upper equator green, lower equator red.
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/orb.htm
Wiggs Patent, from: www.uspto.gov - patent no. 4,553,754


Left Toy Brokers Ltd. / www.rubiks.com circa 2000, right Chinese purchased 2007.
(material, 4.5 inches)
Four loops of eight balls each are arranged in two perpendicular intersecting pairs. Since four of the balls are located at the intersections of the loops, there are a total of 28 balls, seven of each of the four colors (so when solved, each loop has one intersecting ball of its color and one intersecting ball of the other color). Each of the two axles has a button which when pushed in locks the two loops on that axle so that they must rotate together, which gives the puzzle three levels of difficulty (neither pushed, one pushed, or two pushed). Unfortunately, once a button is pushed, that cannot be undone so that someone else can enjoy the easier level (so if you like this puzzle, you may want to get three of them, and leave them set to each of the three levels). The goal is to mix up the puzzle and then put the colors back to the 4 loops. Jaap's Page presents a solution (for all three button states, and which works independent of what state the puzzle was in when a button was pushed), and the puzzle was sold with a solution booklet. Here are photos of the other sides:


Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/rubshll.htm
Solution booklet from Rubiks.com:, from: http://www.rubiks.com/World/Rubiks%20downloads.aspx

Patented by John Haris 1997.
(plastic, 3.5 inches)
This puzzle combines manipulation of the body (changing its shape) with movement of balls. The Harris patent includes figures showing its manipulation and construction. Jaap's Page presents a solution and notes that the inventer is the same person as the designer of Rolling Cubes.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/astrolab.htm
Powerstrike Page, from: http://www.powerstrike.net/puzzles/solutions/astrolabacus.htm
Harris Patent, from: www.uspto.gov - patent no. 5,645,278

a.k.a. Bloxbox, Qrazy Qube
Basic idea dates back to 1889.
(clear plastic box containing 7 red cubes with blue and white dots, 1.5 inches)
A box with 7 cubes and an empty space that allows you to move cubes around by tilting. One must shuffle the cubes so as to have only blue dots touching the faces of the box and three white dots showing in the position with the empty space. There is a little hole in one corner that had a pin inserted into it to prevent the puzzle from being disturbed during shipping. The puzzle is pleasant to use, and doesn't require great dexterity to move cubes. This basic idea is presented in the 1889 Rice patent, and also in the patents of Sinden and Postasy, and the design of this puzzle has been credited to Piet Hein 1972. Jaap's Page presents a solution.
Here are some other versions (the rightmost is a Soviet version). A parity argument implies that not all positions are reachable from a given position, and you cannot exchange two cubes without changing the configuration of the others. So if you try to solve a puzzle of this type and end up with two cubes exchanged, then it must be the other color has to be on the outside.
Further reading:

White with
red/blue dots.
(1.5 inches)
Blue with
red/white dots.
(1.5 inches)
Black with
red/white dots.
(1.5 inches)
Black with
orange/white dots.
(1.5 inches)
White with
red squares.
(1.4 inches)
Jaap's Page, from: http://www.jaapsch.net/puzzles/varikon2.htm
Rice Patent, from: www.uspto.gov - patent no. 416,344
Sinden Patent, from: www.uspto.gov - patent no. 3,841,638
Postasy DE Patent, from: www.epo.org - patent no. DE3027556

Patented by D. Kosarek 1974; 2x2x2 version dates back to 1889.
(clear plastic box containing red cubes with blue and white dots, 2.1 inches)
The center cube and the six cubes that are the center of each of the 6 faces form a single central solid "cross", leaving only 19 cubes that can move around this central cross by tilting the box. Like the Varikon Box 2x2x2, one must shuffle the cubes so as to have only blue dots touching the faces of the box and three white dots showing in the position with the empty space; the puzzle is pleasant to use (and doesn't require great dexterity to move cubes). There is a little hole in one corner that had a pin inserted into it to prevent the puzzle from being disturbed during shipping.
Jaap's Page presents a solution (using a Rubik's cube type notation) that solves the bottom two layers and then solves the top layer by repeatedly exchanging cubes as needed.
This is the same puzzle as Inversion, Inversion, and similar to the Vadasz Cage 3x3x3, a smaller version of Peter's Black Hole, and Mad Marbles. Here are some other versions:

White with red/blue dots.
(2.1 inches)
White with red/green dots.
(2.1 inches)
White with red/green dots.
(2.1 inches)
Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/varikon3.htm
Rice Patent, from: www.uspto.gov - patent no. 416,344
Coe Patent, from: www.uspto.gov - patent no. 785,665
Sinden Patent, from: www.uspto.gov - patent no. 3,841,638
Kosarek Patent, from: www.uspto.gov - patent no. 3,845,959
Postasy DE Patent, from: www.epo.org - patent no. DE3027556


Sold by Toys & International Games, patented by P. A. Roberts, 1985.
(plastic, 2.6 inches)
Like the Varikon Box 3x3x3, but here the 19 cubes are held in place by the edges of the central cross, and you use the puzzle by simply pushing the cubes around. Each cube is colored blue on three sides adjacent to one corner and red on three sides adjacent to the opposite corner. The puzzle is to go between all red and all blue on the outside. Here is what the box back says:



Further reading:
Jaap's Page, from: http://www.jaapsch.net/puzzles/varikon3.htm
Roberts Patent, from: www.uspto.gov - patent no. 4,511,144

a.k.a. Inside Out, Magic Jack, IQ Cube
Peter's Black Hole, circa 1990's.
(plastic, 3.25 inches)
One can reach in with a finger to move cubes inside a cage. The design of the Vadasz cage is often credited to Jozsef Vadasz circa 1995, although this basic idea is described in a number of patents dating back to the early 1900's; the patent of Peter Kassan shows a slightly more complex mechanism with a central cage. These puzzles can be viewed as generalizations of the Fifteen puzzle to three dimensions. It is most fun to use them in a more limited way where you just push from the ends (the only way needed for the 2x2x2 version), but the cubes can be moved individually (and you have to assume that this may have been done when you pick it up after someone else has used it). Jaap's Page gives analysis and a solution.

Vadasz Cage 2x2x2,
Hungary circa 1990's.
(plastic, 2.1 inches)
Vadasz Cage 3x3x3,
Hungary circa 1990's.
(plastic, 3 inches)
Vadasz Cage 4x4x4,
Hungary circa 1990's.
(plastic, 3.75 inches)
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/blackhole.htm
Coe Patent, from: www.uspto.gov - patent no. 785,665
Wooster Patent, from: www.uspto.gov - patent no. 1,518,889
Kosarek Patent, from: www.uspto.gov - patent no. 3,845,959
Kassan Patent, from: www.uspto.gov - patent no. 4,432,548

Circa 1980's?
(plastic, 1.8 inches square by 2 inches high)
This puzzle is similar to (but not the same as) the 3x3x3 Varikon Box, where balls are moved by tilting the box. The colored balls surround a 1 by 1 by 3 unit high core, so that when solved, there are 8 green balls in the bottom layer, 8 blue balls in the center layer, and 7 red balls in the top layer.


Designed and made by J. A. Storer, 2007.
(glued 2 inch plastic golf ball display box containing seven 22mm dice)
These two puzzles work like a 2x2x2 Varikon Box (where cubes are moved by tilting the box), but are easier to solve. Both are shown above in a random state, and for both the goals is:Pick a number and arrange so that number cannot be seen from any side.The black box has a solution for any of the numbers 1, 2, 3, 4, 5, or 6.
The white box can only be solved for 1 or 6 (for each of the numbers 2, 3, 4, and 5, there are four cubes that have this number facing in the same direction)

Patented by W. Clark 1984, made by Innoventures Inc.
(plastic, 1.8 inches)
Like the 2x2x2 Varikon Box 2x2x2 Varikon Box except that through holes in the box a finger can rotate a cube. Jaap's Page observes that it can be solved by first rotating each cube to its correct orientation and then solving like the 2x2x2 Varikon box. Here are the directions on the back of the package:

Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/clark.htm
Clark Frist 1984 Patent, from: www.uspto.gov - patent no. 4,424,971
Clark Second 1984 Patent, from: www.uspto.gov - patent no. 4,488,725

a.k.a. Pionir Cube
Made by Artex, Hungary, 1984.
(plastic, 2 inches)
A total of 67 balls can be moved along tracks one the inside edges of the box by tilting the box (e.g., in a fashion similar to the Varikon 3x3x3 Box); Varikon 3x3x3 Box); there are 7 balls on each edge (with the corner balls being shared between three edges), where one ball is missing. Each side of the box has a paper label with four colored dots on it. All the balls are black, except for 4 red, 4 green, and 4 yellow balls, which in the solved position, must be located in the middle of edges next to the same colored dot on the labels. Jaap's Page presents a solution.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/pionir.htm

Matchbox 1990.
(plastic with internal parts and magnets, 2.7 inches)
Plates inside a hollow cube that have white and red dots on them can be manipulated by tilting the cube; the goal is to make only white dote shown in the holes that have the pattern of a standard die. The 1993 patent of J. Bognar and E. Rubik of a similar mechanism with plated with a single hole on each side into which a finger can be pushed. Jaap's Page describes the configuration of the plates and gives a solution. Here is the English portion of the directions from the back of the box:

Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/rubdice.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/r90/dicenot.htm
Koller's Page, from: http://www.mathematische-basteleien.de/dice.htm
Bognar-Rubik Patent, from: www.uspto.gov - patent no. 5,184,822

a.k.a. Pyramid Piling Puzzle, Brahma Puzzle
Very old design, this puzzle purchased from Bits And Pieces 2007.
(wood stand and seven wood discs, 2.3" by 5.3" base by 3.5" high)
On Post A there are n rings of different sizes, in the order of the largest ring on the bottom to the smallest one on top. Posts B and C are empty. The object is to move the n rings from Post A to Post B by successively moving a ring from one post to another post that is empty or has a larger diameter ring on top.
Solution: Since any of the rings 1 through n-1 can be placed on top of ring n, all n rings can be moved by invoking the recursive procedure TOWER:procedure TOWER(n,x,y,z)TOWER(n,x,y,z) makes 2n-1 moves; e.g, TOWER(3,A,B,C) takes 7 steps:if n>0 then beginTOWER(n-1,x,z,y)end
write "Move ring n from x to y."
TOWER(n-1,z,y,x)
end
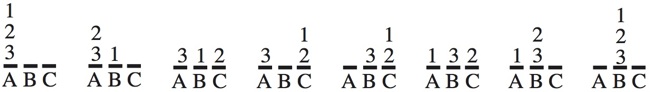
"Unwinding" the recursion of TOWER, yields the following simple iterative algorithm that moves the discs on post in the clockwise direction:if n is odd then d := clockwise else d := counterclockwise
repeatMove the smallest ring one post in direction d.
Make the only legal move that does not involve the smallest ring.
until all rings are on the same post

Pyramid Piling Puzzle, Well-Maid Wood Products, Suffield, CT, unknown age.



(cardboard box 3.7" x 5" x 3/4", wood base and pieces, directions, infor. sheet;
the discs were lost at some point and replaced)



Rainbow Puzzle, unknown age.
(2.5" diameter by 1.6" wood box with three 3/16" diameter 2" long wood pegs,
and 8 wood discs, from 11/16" diameter to 1+15/16" diameter;
to play, turn box over and put pegs into the holes in the bottom)
Further Reading
Excerpt from J. A. Storer's book.
Wikipedia Page, from: http://en.wikipedia.org/wiki/Towers_of_hanoi
Wolfram Mathworld Page, from: http://mathworld.wolfram.com/TowerofHanoi.html
Claus Page, from: http://www.cs.wm.edu/~pkstoc/toh.html
Ajtai Patent, from: www.uspto.gov - patent no. 5,992,851

a.k.a. a.k.a. Cardan's Rings, Baguenaudier
Very old design, this one owned by J. A. Storer's grandfather, circa 1900?
(2.4 by 8.5 by 1.75 inches high wood box with key and 6.5 inch long puzzle)
Each ring is attached to a post and, except for the rightmost ring (the one farthest from the handle), each goes around the post to its right (and under the ring to its right). Rings that are not on the skewer can pass sideways through the skewer. Initially, the skewer goes through all the rings. The goal is to remove the skewer from the rings (and then put it back).
Solution: Observe that the only two ways to move a ring are to put the rightmost ring on or off the skewer, or, a ring can be put on or off the skewer if and only if the ring to the immediate right is on but all other rings to the right are off. This leads to a simple iterative solution in a similar spirit to the Towers Of Hanoi puzzle; we use the phrase "complement a ring" to mean take it off if it is on or put it on if it is off:Take the rings off:Start with all rings ON.Put the rings on:
repeatMake the only legal move that is not complementing the rightmost ring.
Complement the rightmost ring.
until all rings are OFFStart with all rings OFF.
repeatComplement the rightmost ring.
Make the only legal move that is not complementing the rightmost ring.
until all rings are ON
Gray codes of n bits are a binary counting system where only one bit changes from the representation for an integer i to the representation of i+1, 0 &le i &le 2 n - 1. Let B(i,n) denote the standard binary representation of i using n bits, G(i,n) the Gray code of n bits, XOR the exclusive or operation, and ShiftRight the operation of shifting the bits of a code one position to the right (discarding the rightmost bit and setting the leftmost bit to 0). Although Gray codes are not in general unique, a standard form is one where:G(i,n) = B(i,n) XOR ShiftRight(B(i,n))Here is the correspondence for n=4;
all 4 bit binary sequences are shown, but we only need entries 0 through 10:Observe that when going from one row to the next, every other time it is the rightmost bit that changes, and for the other times a bit changes where the bit to its right is 1 and all bits to the right of that are 0. Hence, if we let 0 denote a ring off and 1 denote a ring on, then one can see that the Gray code sequence corresponds to our solution for the Chinese rings; that is, for the case of 4 rings, taking them off corresponds to moving from row 10 to row 0 in the above table, and putting them on corresponds to moving from row 0 to row 10.
The number of moves to put the rings on or off is the same, so let's count the number of moves to take them off. We can express our iterative solution recursively as follows:Represent the rings as an array R[1] .. R[n] where R[1] corresponds to the leftmost ring, and R[i] is 0 if the corresponding ring is off and 1 if it is on. Let FLIP(i) denote complementing R[1] through R[i], then set all positions to 1 and call FLIP(n):The number of moves M(n) for FLIP(n) is given by the recurrence relation:
procedure FLIP(i)
if i=1 then Complement R[1].
else if i=2 then Complement R[1] and R[2].
else doFLIP(i-2)
Complement R[i].
FLIP(i-2)
FLIP(i-1)
endM(n) = M(n-1) + 2M(n-2) + 1Two simple proofs by induction, one for when n is even and one for when n is odd, can now be used to show that the solution is:(2n+1-2)/3 if n if n is evenThe first few values of M(n) are:
(2n+1-1)/3 if n if n is odd1, 2, 5, 10, 21, 42, 85, 170, 341, 682. ...For the puzzle pictured here, which has seven rings, the solution is 85 moves.
Note: Sometimes people count the moving of the two rightmost rings as one move, in which case it can be shown that the number of moves is reduced to:2n-1-1 if n is evenAnd now the first few solution values become:
2n-1 if n is odd1, 1, 4, 7, 16, 31, 64, 127, 256, 511, ...






Patented by W. Keister 1972, made by Binary Arts / Think Fun.
(plastic, 12.5 inches)
There is a bar with knobs on it in a track. There is only one position along the track where a knob can be turned. When all of the knobs are turned horizontal (curved end to the left in the photo above) the bar can slide all the way out. There are only two possible moves at each point, and so to solve, one can repeatedly choose the move that does not return the puzzle to the previous position. Start by turning the rightmost knob.
The original version is shown first above. Binary Arts, which became Think Fun, later made the one shown second above, which allows the knobs to be reset (by flipping down the end and sliding out the bar); this one was purchased in 2008.
Jaap's Page presents this puzzle, which is essentially the same puzzle as the Hexadecimal Puzzle (described in another Keister patent) and the Chinese Rings (see that page for information about Gray Codes and additional links).
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/spinout.htm
Keister Patent, from: www.uspto.gov - patent no. 3,637,215

Patented by W. Keister 1972, made by Binary Arts.
(Cherry, 8.75 inches, in a 6.2 by 10.75 by 2.2 inch cardboard box)
There are eight bars that can either be up or down; and four fingers that can be either up (one) or down (zero). In the photo below, the leftmost two bars are up, the third bar from the left is down, the fourth and fifth bars from the left are up, the rightmost three bars are down, the left three fingers are up (three ones), and the rightmost finger is down (a zero). The assembly that holds the bars cannot slide out to the right and can only slide out to the left if all the bars are up. The finger assembly can be pushed in (it is spring loaded) to cause a center portion of the back edge to go back, allowing the bar that is lined up with the right edge of the finger assembly to move up or down; the difficulty is that the finger assembly can only push in when each 1-finger is aligned with a down bar and each 0-finger is aligned with a down bar (or the finger is to the left of the bars); in the photo below, it can be pushed in. The fingers can be set to any of the sixteen possible patterns by pulling out the peg that runs through them and rotating each as desired. The corresponding sixteen puzzles all have the goal of starting with all bars down, and sliding the finger assembly out to the left. Setting 1111 allows the bars to be moved up one at a tome and the bar assembly easily slid out. Setting 1110 is the hardest setting, which gives a puzzle equivalent to the Chinese Rings, and requires 170 moves.

The setting of 1110 that requires the longest sequence of moves can be solved exactly like Spinout (described in another Keister patent) or the Chinese Rings puzzle (see that page for information about Gray Codes and additional links), where moves alternate between the rightmost bar and the only other legal move. Shorter solutions for the other patterns can be solved by along the lines of the hints card provided with the puzzle. Jaap's Page gives some history of this puzzle (it was the first puzzle made by Binary Arts, which became Think Fun), cites an article about the inventor, and presents minimal solutions for each level, as well as some additional analysis of the solution space diameter (the maximum number of moves to go between any two positions, not necessarily the start and end positions); here is a table of the minimal solution lengths:
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/hexadec.htm
Keister Article, from: http://www.puzzles.com/products/ElephantSpinOut/ElephantInventor.htm
Keister Patent, from: www.uspto.gov - patent no. 3,637,216

Designed by Vilmos Serestey and sold at the Atlanta 1996 Olympics.
(plastic, 25 rings + base, 7 inches wide by 3.5 inches tall)
Five rings of each color numbered, 1 through 5. The only two legal moves are to move 2 rings at a time or to move 3 rings at a time. The posts are only long enough to hold 7 rings. After mixing up the rings, get them back to the solved puzzle where rings of each color on their correct base, arranged in order from 1 on the bottom to 5 on top. An easier puzzle is to ignore the numbers. Another puzzle is get five colors on each post (in the same order).
A Solution: Assume we start with 5 rings on each post (if not, it is always easy to make it so). The following sequence temporarily "parks" the top ring of one post (call it A) on another post (peg B):
- PARK: Move 2 rings from B to A, then move 3 rings from A to B.
(You can also "double park" by repeating this operation twice.)
- UNPARK: Move 3 rings B to A, then move 2 rings from A to B.
(If double parked, repeat this twice, or if another post C currently has only 5 rings, you can put back the two rings in reverse order by moving 2 rings from B to C, 2 rings from B to A, and 2 rings from C to B.)
Using this idea, we can do the following two key transformations:
- The top rings of any two posts can be exchanged.
(In fact with double parking you can exchange the top two rings).
- The rings of a given post can be permuted in any order. (The top 4 can each be parked on the other four posts so that they can be put back in any order. If the bottom ring also needs to be moved, it can be double parked with one of the rings that is going to one of the top 4 positions.)
The ability to permute the rings of a post combined with the ability to exchange the top rings of any two post suffices to solve the puzzle. Of course, additional shortcuts can be devised.

Designed by Toshio Akanuma, originally made by TRICKS Co. Tokyo Japan, 1983;
this one made by J. A. Storer, 2009.
(Ebony, Walnut, Purple Heart, Apple, brass, 2" x 8" x 3.75")
In the theme of the Towers Of Hanoi puzzle, but with a more complex analysis. Exchange the 4 tiles on levels 1, 2, 3, 4 on the left (marked with brass screws) with the 4 tiles on the corresponding levels on the right; tiles must be moved by sliding off one post and on to another, where the posts are long enough to hold a tile at level 5. The puzzle is constructed so that no tile can move below its initial level.
The original version made in 1983 has 10 identical tiles on each side that move in a board, where tracks on the back of the tiles enforce the condition that no tile can move lower than its first position. Baxter's Page has references to an analysis of the general solution for a puzzle of n tiles on each side (see also Jaap's Page), and Baxter's paper gives the following table of the number of moves required for puzzles of size 1 through 10 (where the entry for 10 is an upper bound and the others have been verified by computer to be optimal).
Further Reading
Baxter's Page, from: http://baxterweb.com/puzzles/panex
Baxter's paper, from: http://baxterweb.com/puzzles/panex/panex2rev.pdf
Jaap's Page, from: http://www.jaapsch.net/puzzles/panex.htm
Manasse and Sleator paper, from: http://baxterweb.com/puzzles/panex/panex-v1d.pdf
Manasse, Sleator, Wei, Baxter paper, from: http://baxterweb.com/puzzles/panex/panex5.pdf
Panex Search Program, from: http://baxterweb.com/puzzles/panex/program.htm
Bagley Play Panex Page, from: http://gwyn.tux.org/~bagleyd/java/PanexApp.html
Henderson Play Panex Page (4 high), from: http://www.cheesygames.com/panex


Patented by D. Rom 2004, made by elogIQ.
(plastic, left 5 inches with 1" balls, right 3.5 inches with 1" balls)
Comes in the standard 3 x 3 version (which was also made in a clear body) and the mini 2x2 version. Rotating a ball up or down makes all balls in the same column rotate the same way, and rotating a ball left or right makes all balls in the same row rotate the same way. Each ball has six colors.; the goal is to mix up the puzzle and then restore it to each side having a single color facing up. The puzzles come with solution hints, and Jaap's Page presents a solution. Here are what the reverse sides of the two puzzles look like:


Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/cmetrick.htm
Rom Patent Application, from: www.uspto.gov - application no. 2004/0000756

Patented by D. Rom 2004, made by elogIQ.
(plastic, 3.5 inches with 1.5 inch diameter balls)
Each of the six balls can rotate in each of the three directions. Each pair of adjacent balls shares a disc (so there are a total of 20 discs), and rotating a ball causes the shared disc or discs to move and be replaced. When solved, each ball shows a single color (red, blue, green, or yellow) and the hidden discs are all white.
A harder version of the puzzle, called Cmetrick Too Hard (two views shown below), has dots in the middle of the discs that must be the same color on each side of the puzzle when solved.


The puzzles come with solution hints, and Jaap's Page presents a solution.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/cmetrick.htm
Jaap's Contest Page, from: http://www.jaapsch.net/puzzles/cmetrick2c.htm
Rom Patent, from: www.uspto.gov - patent no. 6,773,011

Designed by Oskar van Deventer, made by Recent Toys International; the box this one came in says copyright DaMert Co. 2005.
(plastic, each edge is 3.5 inches)
Four balls each have a number of circular depressions that allow them to be packed tightly together inside a pyramid shaped cage. A ball can rotate only if it sits in the depressions of at least two other balls. The goal is to rotate the balls so that each side is a single color (red, green, blue, or yellow). Here are the other two sides:

By observing that the green and blue faces have only one depression, Jaap's Page observes that a relatively simple solution proceeds by solving green and blue first (to allow more depressions available for the remainder of the solution). That is, position the red-green-blue corner, then the green-blue-yellow corner, then the third planet on the blue side, and finally the remaining planet, where the last step may require some temporary rotations of the other balls.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/planets.htm


Patented by L. A. M. J. DeBergh 1996, made by LD Games, Belgium.
(plastic, 4.5 inches by 7/8 inch thick;
one the bar it says "SATURN 2x4 colors",
and on the other side of the bar is says "LD Games Belgium Patented C 1994")
Each side of the ring has 16 discs, where each of the 64 disc sides are colored with one of 14 colors. The goal is to have exactly 4 colors showing on each side (arranged in 4 sets of 4) for a total of 8 visible colors, where the remaining 6 colors are hidden. This puzzles is really a pencil and paper problem of determining which of the 14 colors are the 8 visible colors (see the next page); for the white body puzzle above they are:Visible: yellow, pink, magenta, purple, light green, green, blue, grayOnce the 8 visible colors have been determined, solving the puzzle is very easy. The bar across the center in the photos above, which the directions refer to as the "switch", is in the solved position that prevents the puzzle from being mixed up. Rotating the switch along its axis 90 degrees exposes a track on both sides. The first two positions on each side can each be used to temporarily park one or two discs, and the third position on the track allows a disc to pass from one side of the track to the other. Rotating the switch 180 degrees allows one to exchange discs from top to bottom or flip a disc:
Hidden: white, orange, red, light blue, brown, black
(Black body is the same except that brown visible and gray hidden.)




To solve:
- Flip all discs that have a hidden color showing.
- If a color is showing on 5 discs (all colors are on at most 5 sides), find the disc that does not have a hidden color on the reverse side and flip that one.
- Exchange discs one or two at a time until only four colors show on each side.
- Rearrange colors on each side into any desired pattern (e.g., 4 groups of 4).
Flip each disc to make a list of 32 color pairs that are comprised by the discs (see the next page). The number of times each color occurs is:

We refer to the colors that appear only 4 times as the sparse colors. The puzzle is not so simple as the 6 sparse colors are the 6 hidden colors.
A key observation is that If a sparse color is hidden, then all colors that appear on the opposite side of a disc with that sparse color must be visible. To determine which are the visible colors, we can employ some simple deductions. This is for the white body puzzle; similar logic for the black body with brown and gray reversed:Jaap's Page gives a similar solution (that motivated this one).
- There are two discs that have a sparse color on both sides, (brown, gray) and (brown, pink). It turns out that brown is hidden and gray and pink are visible (if we had guessed incorrectly and chosen brown as visible, then in the following steps one quickly reaches a contradiction where there is a color that can be neither visible or hidden).
- Brown is also paired with green and yellow, so at this point we know that 4 of the visible colors are gray, pink, green, and yellow.
- By checking our list of 64 pairs, we see that blue is paired with 4 additional colors (red, black, light blue, and white) and so if blue was hidden, that would add 4 more visible colors, making a complete set of eight. But this cannot be possible, because now light green, for example, cannot be visible (because that would make 9 visible colors) and cannot be hidden (because light green is paired with orange which is not one of these 8). Hence blue must be the 5th visible color.
- Similar to step 3, light green must be the 6th visible color.
- Similar to steps 3 and 4, magenta must be the 7th visible color.
- Similar to steps 3, 4, and 5, purple must be the 8th visible color.
Here is a tabulation, listed in alphabetical order, of the disc colors that appear in the two puzzles show in the photos on the first page. Although both have the same numbers of each color, the pairings are not the same:

Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/saturnld.htmm
DeBergh WO Patent, from: http://www.wipo.int - patent no. 0,000,000

Patented by S-H Juang, 1988.
(plastic, 2.8 by 11/16 inches)
Each of the 12 windows is positioned over a little drum that can be rotated to show one of the four patterns red square, green circle, blue triangle, or yellow squiggle. Three of the windows are marked with four dots on the outer edge (in the photo above, going clockwise from the top, the marked windows are at positions 2, 5, and 9). Rotating the front face clockwise one position causes the drums in each of the three marked windows to cycle by one pattern. Rotating the front face counter-clockwise repositions the windows without rotating any drums.
For example, if R denotes a clockwise rotation and C a counter-clockwise rotation, then repeating the two moves RC four times cycles the drums of the three marked windows four times (causing each to show the other three patterns and return to the pattern in which it started), and leaves the state of the puzzle unchanged.
The goal is to make all the windows show the same color. Jaap's Page gives a solution that can be used to solve for any of the four colors.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/orbik.htm
Juang Patent, from: www.uspto.gov - patent no. 4,752,074

Designed by John Harris, circa early 1970's.
(plastic, each cube is 1" square, box is 3.5" x 3.5" x 1.25")
Eight identical cubes can be flipped around (via the ridges on the tray); the go al is to mix them up and then restore to have the same color on top and the middle empty. This puzzle is similar to Cross Teaser. The tiles snap off if want to make a different puzzle. Jaap's Page presents a solution and describes the puzzle, noting that it was discussed in Martin Gardner's Mathematical Games column in Scientific American March and April 1975. He also notes that the designer is the same person as that for Astrolabacus.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/index.htm

Tobar Co. Challenge Games 2006; also sold by Recent Toys Internatioal.
(plastic, 4.75 inches diameter by 1 inch thick)
Eight three dimensional cross pieces each have a tip facing the top, a tip facing the bottom, two tips facing horizontally, and two tips facing vertically. A move consists of flipping a cross towards the empty position. For example, in the photo above, the cross in the center of the top row can be flipped down to the middle, leaving the to horizontal ends the same, causing the top and bottom tips to face vertically, and causing the formally vertical tips to face the the top and bottom. The goal is to mix up the puzzle then restore it so that there is a single copor of tips facing the top and a single color facing the bottom. The solved puzzle shown above has red tips on top, and below is a photo of the other side that has blue tips. This puzzle is similar to RollingCubes. Jaap's Page presents a solution.

Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/crosstsr.htm


Copyright Matchbox 1988, patented by C. Wiggs and C. Taylor 1989.
(plastic, 4.25 inches diameter by 1 inch thick)
Nine clocks are on each side (the reverse side is shown on the right above) are arranged in a 3 by 3 array with a yellow button and a knob at each corner. Each of the four yellow buttons can be up or down. Turning each of the four knobs on the side of the clock spins some subset of the clocks that depends on the buttons (all turn clockwise or counter clockwise depending on the direction the knob is turned), according to the following rules:
Adjacent to a down button: Turns all corner clocks adjacent to a down button.
Adjacent to an up button: Turns all corner clocks adjacent to an up button and for each of these corner clocks, the three clocks closest to them also turn.
The goal is to mix up the puzzle and then restore both sides to have all hands pointing up. Jaap's Page presents a solution that essentially solves one side at a time as follows:
- Make all non-corners point the same way: Put the top two buttons up, the bottom two down, and turn a top knob until the center clock matches the bottom middle clock (note that the bottom middle does not move and only the corners on the reverse side move); repeat three more time on successive 90 degree rotations of the puzzle.
- Make all non-corners point up: Put all buttons up and rotate all non-corners to point up.
- Repeat step 1 on the reverse side.
- Synchronize the corners on the reverse side: Since the corners are always the same on both sides, this step will synchronize corners on both sides, but be sure to do this from the perspective of the reverse side. Put the top left button down, the other three buttons up, and turn the top right knob until the center clock matches the upper left clock (note that the upper left clock does not move and the others all move together); repeat three more time on successive 90 degree rotations of the puzzle.
- Repeat Step 2 on the reverse side.

Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/clock.htm
Safalra's Page, from: http://www.safalra.com/other/rubiks-clock-solution
Stefan Pochmann's Page, from: http://www.thedryeraseboard.com/mechpuz/rubiksclock/solution
Dry Erase Board Page, from: http://www.stefan-pochmann.de/spocc/speedsolving/clock
Christian Eggermont's Page, from: http://web.inter.nl.net/users/C.Eggermont/Puzzels/Clock.html
Wiggs Patent, from: www.uspto.gov - patent no. 4,869,506

Mag-Nif Inc., 1989.
(plastic, 4.1 inches by 1.75 inches high)
Six red buttons can be pushed into one of three vertical positions; when the correct combination of positions is achieved, the puzzle comes apart into three sections. Here are views of the bottom of the puzzle and the bottom of the box, which invites you to purchase a solution sheet:


Solution: Leave every other button at the top position and push the other three to the middle position (none of the put-ons are pushed to the bottom position). The sections can then slide apart by pushing two opposite places on the top in directions roughly 90 degrees to each other.

Designed by William Hu, made by Eric Fuller 2014.
(Maple, Jatoba, Acrylic, 3+3/8" x 4" x 1+1/8";
the body is 5/8" thick and the square come out of both sides by 1/4")
Here is what the maker says about the puzzle:"Even though I knew it would be a difficult project, I couldn't resist making this puzzle. It's a very unique concept and execution. The acrylic maze piece must be removed, and the three key pieces are simultaneously manipulated to achieve the goal. Very tricky and very interesting looking, this puzzle begs to be solved. Construction was tricky...the solid side spine and endgrain key pieces were fun to make, but very labor intensive. Fit is excellent; should not have any issues with humidity. 42 made for sale, each signed and dated." With the humidity ok, one can hold the puzzle vertically and manipulate the squares to cause the plastic maze to fall down and eventually out. The idea and construction are very nice but solving is a painstaking process where the positioning of the pieces must be absolutely precise with respect to portions of the plastic maze that you cannot see. So I have not attempted to do it ..."Much of the plastic maze is hidden at any time, and things have to be lined up exactly to move; here is a photo of the maze starting to come out:


a.k.a. Mind Twister
Patented by Y-J. Husn, 1993.
(plastic, 3.25 inches)
Each of six rotating discs has slots to hold eight numbers. In the solved position, each disc has the numbers 1 to 8 of its color in clockwise numerical order, except the white disc which has the number 1 to 7 in clockwise numerical order and one empty slot. Where two discs are tangent and one of the discs has an empty slot at that position, the number of the other disc at that position can be slid into the empty slot. The object is to mix up the puzzle and then restore to the solved state. Jaap's Page presents a solution. Here is a photo of the other side of the puzzle:

Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/wisdom.htm
Hsun Patent, from: www.uspto.gov - patent no. 5,215,305

a.k.a. SpongeBob Cube
Burger King promotional item, 2004.
(plastic, 2.5 inches)
An easy but fun puzzle where the top and bottom halves can be rotated with respect to each other and a piece can be slid up and down. Jaap's Page observes that this puzzle is like a 2 high by 4 column Whipit Tower where all pieces are different (or similar to a small Babylon Tower), and presents a solution.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/spongebob.htm

Designed by Ferdinand Lammertink, copyright ThinkFun 2005.
(plastic, 3 inches by 6.25 inches with 1.5 inch diameter wheels)
Two tracks, each with five squares, can slide horizontally to three positions (left, center, and right). Each square has the same number on both sides, A pair of wheels on either side of the central 2 by 3 array of numbers can be used to flip them. The basic goal is to make the pattern 0 to 9 (i.e., 0 to 4 on the top row and 5 to nine on the bottom row). The directions also challenge you to make other patterns.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/flipside.htm
Passion For Puzzles Page, from: http://www.passionforpuzzles.com/puzzles/flipside.php

Hungarian circa 1980s?
(plastic, 3.25 inches)
Two openings in the clear outside shell allow fingers to be used to rotate the inner ball. The inner ball has pentagons with holes in them and the outer ball has dots. The goal is to rotate the inner ball so that each dot is inside a pentagon hole.


a.k.a. Rubik's Hat
Matchbox circa 1994.
(plastic, 2.4 inch top, 3.75 inch rim, 3 inches high)
Six discs, each with nine slices, can be rotated. In the initial position, with the letters* R u b i kin a vertical line down the outside, no rabbits are visible when turning over the hat and looking in the bottom with light behind. The goal is to rotate the discs so that nine rabbits, one in each slice, can be seen. Jaap's Page gives an analysis that shows the following solution to be unique (this view looks inside with the rim of the hat facing up):
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/rubrab.htm


Purchased from Rubik Fans 2007; a similar puzzle is described in the patent of R. Massimiliano 1996.
("Type 1" and "Type 6" puzzles, plastic, 3.25" diameter, 7/8" thick)
On top of the puzzle, eight outer circles and a center circle with ring around it can be rotated (there are no circles on the bottom). There are two dials, one around the edge of the top and one around the edge of the bottom (the center ribbed portion of the puzzle is just for holding it). Internal gears are arranged in a way so that the two dials can rotate different portions of the puzzle. This puzzle has been made with different graphics and different arrangement of internal gears. For example, with the "Type 1" puzzle shown on the left above, the top dial rotates 4 consecutive outer circles and the center ring, and the bottom dial turns rotates all eight outer circles and the center ring / circle combination (also, the entire center platter rotates slowly as the botom dial is rotated).
Jaap's Page describes an Enigma puzzle with an arrrangement of gears that rotate disjoint subsets of circles / rings, and having taken it apart, gives the number of teeth on the gears. The general idea of his solution, which seems to apply to all of these puzzles, is to start by solving a portion and then turn rings a number of times to match up with common multiples of ring revolutions.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/enigma.htm
Massimiliano WO Patent, from: www.epo.org - patent no. WO9602307


Copyright Maf-Nif Inc. 1989.
(5.5" x 5.5" x 3.2" cardboard box, 5" diameter by 2.8" high plastic puzzle)

Two dimensional manipulation puzzles include the movement of square pieces (e.g. Fifteen), rectangular pieces (e.g. Traffic Jam), rectilinear shaped pieces (e.g. Neo Black and White), balls (e.g. Hungarian Rings), pieces that can carry other pieces (e.g. Trap), and tokens (e.g. TeeZ), where sometimes movement may be mechanically assisted (e.g. Top Spin).
For the number of moves of a sliding block puzzle solution, cost metrics include:Unit: one move = slide one piece one unit horizontally or verticallyOne finger rule: These rules work by pushing a single piece with one finger, and do not allow a piece to push other pieces. However, when noted, generalized movements may allow other pieces to be pushed as the piece pushed by the finger moves (for example, when one piece has another one caught inside it and drags that piece along with it, when sliding a row of pieces is natural for a puzzle, or to shorten the presentation of a puzzle solution).
Straight-line: one move = slide one piece any distance horizontally or vertically
Rectilinear: one move = slide one piece along a rectilinear path


a.k.a. Game of Fifteen, Sliding Numbers, Gem Puzzle, Boss Puzzle, Le Taquin, ...
Old idea dating back at least to circa 1880, this version copyright ThinkFun 2000.
(metal with plastic case, 2.5 inches; keychain 1.75 inches)
Packaged with 1 through 15 arranged by row (lower right empty). After sliding pieces to mix it up, one must return to the starting position. The back of the box says that this one reproduces a 1933 design called the IMP:


To solve, the top two rows are easy, then cycle the last two rows, taking "short cuts" as needed to rearrange the order of pieces in the cycle.
Here are some other problems from the back of the ThinkFun Mini Fifteen keychain. The first, to make a magic square with the empty square counting as 0, is the Spanish Dungeon of H.E. Dudeney 1917 (see Baxter's Page). The last, the reversing problem, is noted as impossible:


The Fifteen-Fourteen Problem is starting with the puzzle solved with the empty square in the lower right, slide the pieces to exchange 15 and 14, leaving the puzzle otherwise solved and with the empty square again in the lower right.


Fifteen-Fourteen, used by J. A. Storer as a child circa 1965.
Can't be solved with the empty square lower right, but can with it upper right.
Both of these positions have odd parity.
(plastic, 2.5 inches)
After the Fifteen puzzle appeared in the 1880's it was not widely known that the 15-14 puzzle was not solvable (no internet then!). Puzzles commonly sold could have the pieces removed and then put back in a random position (with a 50-50 chance of being solvable). As late as the 1930's there were even prizes offered. for various solutions.
A parity argument shows that half the puzzle positionss cannot be reached from any given position (e.g., see the Wikipedia Page):Number the rows 0,1,2,3 going from bottom to top. The count of a position is the row number of the empty square plus the number of pairs of pieces that are out of order. The parity of a position is even if its count is even and odd otherwise. Moving a piece one left or right does not change the position count (does not change the empty square row number or the ordering of pieces). Moving a piece vertically always changes the position count by 4 because it changes the empty square row number by 1 and order with respect to 3 other pieces (either moving up due to the squares on its left and on the right above, or moving down due to the squares on its right and on the left below). Since both 0 and 4 are even, all positions reachable from a given position must have the same parity. In particular, the 1 to 15 position cannot be reached from the 1 to 15-14 position because these two positions have different parity.Parity can be used to see that the Fifteen Reversed problem is not solvable. The solved 15 puzzle start position has count 0 (even number) whereas the reversed solution has count 0+1+2 + ... +14 = 105 (odd number). But it can be done with 1 and 2 switched (reducing the count to 104).



"The Cross Number", circa early 1900's?
(wood box and 15 wood pieces, 4+3/8" x 4+3/8" x 1/2";
directions on top specify a solvable version of the Fifteen-Fourteen problem)
Old versions of the fifteen puzzle typically had pieces that could be removed, and sometimes a piece 16 was included that was not used to play the normal fifteen puzzle, or left in for making a magic square, of the numbers 1 to 16, defined as an arrangement so that the four rows, the four columns, and the two diagonals all sum to 34. One example is the Boss puzzle shown on the next page, which refers to this as the "Thirty Four" problem. Here is another:


"Le Taquin", manufactured by JJE Paris, circa 1880's?
(wood box and 16 wood pieces, 3.9 by 3.9 by 3/4 inches;
shown on page 61 of the Fifteen book,
the French directions on the inside top cover describe both 15 and magic square)
The idea of magic squares dates to over a thousand years ago; here are two old designs shown on the Wikipedia page:
The Winning Ways book (page 778-783) discusses the design of 4x4 magic squares and notes that the 880 ways to do it for the numbers 1 to 16 (not counting reflections and rotations) was worked out in 1693 by Frenicle de Bessy; see also the Wolfram Mathworld page.
Many puzzles sold combined problems for fifteen and sixteen pieces; here are the front and back of directions that came with a "2 puzzles in 1" keychain puzzle:






"BOSS THE NEW GAME OF FIFTEEN", W. H. Cremer, London, 1880.
(cardboard box and 16 wood pieces, 3.5 by 3.5 by 5/8 inches;
15 diagram on underside of the box top, and 17 page booklet about the 34 puzzle;
similar to the puzzle shown on page 73 of the Fifteen book)
This clipping was tucked into a copy of the 1893 Hoffmann book; from the text on the reverse side, it appears to be from a February 13, 1880 issue of an Albany newspaper.



Shown on page 102 of the Fifteen book. This 2.5 inch square metal puzzle was made in the 1933 to 1934 time frame in a number of similar variations, including different pegs on which the pieces slide (round vs. square), different colors, different text on the sides of the puzzle, different cases (shiny vs. textured red), similar but different booklets (all are 2.25 inches square with the same cover graphics), and even a braille version.
Many fun and promotional versions of the Fifteen puzzle have been made with graphics of some kind rather than numbers. Sometimes the graphics are such that every square is unique, and so it is really exactly the same puzzle as the standard Fifteen. However, when there are two pieces that are identical, as is the case with each of the four Warner Brothers puzzles shown below, it is possible to be stuck at a configuration where the puzzle is finished except that two adjacent pieces are out of order. In this case, solve the puzzle with the positions of the two identical pieces exchanged. For example, for the bugs bunny puzzle shown below, the pieces that go in positions 5 and 9 are identical (note that this is not the case for positions 8 and 12 because piece 12 is not quite blank); if you are not able to complete the last two rows because of this problem, move the blank piece that appears to go in position 9 to position 5 (causing the blank piece that was in position 5 to now be in the last two rows), and now solve the last two rows.

"Digit", Roalex Co., Forest Hills, NJ, circa 1950's and 1960's.
(card is 4.4 by 5.6 inches, puzzle is plastic 2.5 inches by 1/4 inch thick)
A similar puzzle was made by Plastrix.




"Popeye", "Superman", "Yogi Bear", "Pebbles",
Roalex Co., Forest Hills, NJ, circa 1950's and 1960's.
(card is 5 by 6 inches, puzzle is plastic 2.5 inches by 1/4 inch thick)
The Roalex Co. made numerous Fifteen puzzles based on cartoons and TV shows; some based four related characters in each of the columns (such as the popeye puzzle above) and some on individual characters (such as the Superman puzzle above that J. Storer played with as a child). These puzzles on their original cards (which sometimes had an extra piece on top) are a popular for collectors (see further reading).

Roalex Co., Forest Hills, NJ, circa 1950's and 1960's.
(card is 6.1 by 5.3 inches, puzzle is plastic 2.5 inches by 1/4 inch thick)
Although many Roalex cards were horizontal ones of an approximate shape of width 1.25 times height as with the version of Popeye on the preceding page, other shapes were used, including a shape of about height 1.14 times width, such as this version of Popeye.
Here is what is on the back of the Popeye card of the preceding page:


"Gem Puzzle No. 0", Matthias Rice, December, 1879.
(3.25 inches square by 1/2 inch thick cardboard box and 15 wood pieces;
shown on the cover page, page 8, and page 11 of the Fifteen book,
which dates this puzzle and gives some history)
The top of the box top says "THE GEM PUZZLE No. 0", the bottom of the box top says "Place the Blocks in the Box irregularly, then move until in regular order.", the left and right sides have been scratched out on this one, but originally on the left side was "MANUFACTURED BY M. J. RICE" and on the right side "For CARY, FULTON & Co., No. 29 Kingston Street, Boston."
Although the theme of the Fifteen book is that the origin of the Fifteen puzzle is unknown, it does indicate that the high popularity of the puzzle in the 1880 time frame started with this production of the puzzle in December of 1879, and describes a March 1, 1880 interview of Mr. Rice published in the Boston Herald that describes how he got the idea for making the puzzle from a version made in Hartford by deaf students, and sold for 75 cents apiece.


"Drueke's 15 Puzzle", Wm. F. Drueke & Sons, Grand Rapids, Mich.", circa 1960's.
(plastic, 2.5 inches square by 3/16 inch thick)




"15-Puzzle", Rudolph Steiner, NY, circa 1950's.
(cloth pouch, plastic puzzle, and cardboard instructions, 2.5 inches;
the back says THE "15-PUZZLE", ARRANGE NUMBERS. HORIZONTALLY, VERTICALLY,
DIAGONALLY, OR IN SPIRALS, ETC., PAT. APPLIED FOR, RUDOLPH STEINER CO., N.Y.C. U.S.A.)




"Lowe's 15-Puzzle", 1950's.
(felt lined pouch, plastic puzzle, and cardboard instructions, 2.5 inches;
shown on page 103 of the Fifteen book)

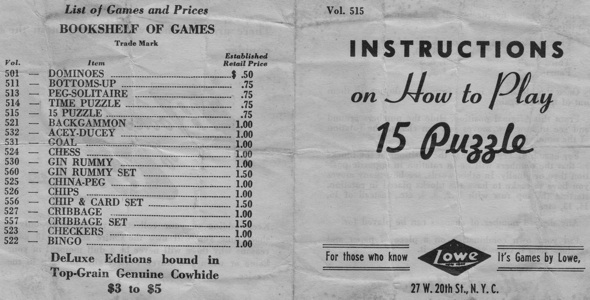

"15 Puzzle", Lowe's, circa 1940?
(4.75" square by 1" leather covered box with fifteen 1" square by 1/2" wood pieces)

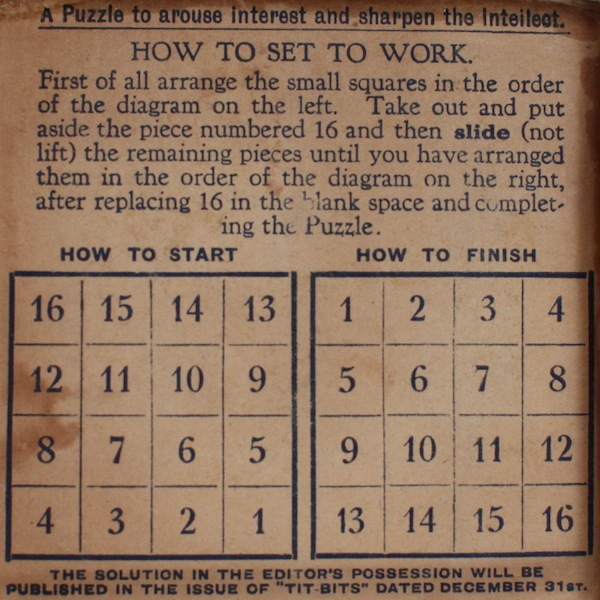
"Great 16 Puzzle", Tit-Bits Teaser No. 6, circa 1930's.
(wood pieces in cardboard box, 3.6" square x 3/8" thick)



"Celebrated Fifteen Puzzle", Fairy Queen Steamer, circa late 1800's?
(wood pieces in hinged wood box, 2.3" square x 3/4" thick)
The Fairy Queen steamer boat is mentioned in the 1885 Thorough Guide Series for Scotland; here is an excerpt from page 185:


Wood box with inlay of dancing couple and 15 wood pieces, 1837 ???
(4.6 inches square by 1 inch thick, pieces are 1 inch square by 1/4 inch thick,
the date 1837 is hand written on the back)
This box has a beautiful inlaid top showing a dancing couple and looks quite old. The date of 1837 written on the back raises the fun possibility that this puzzle pre-dates the 1880's Fifteen puzzle craze that is documented in the Fifteen book. However, it is hard to give this date too much weight; it could have been written by anyone at anytime. Below are photos of the inside, which looks quite similar (including the hinges) to the inside of the Souvenir d'Egypt puzzle (made in France) that is shown on page 97 of the Fifteen book.





"Calculator Puzzles", England, circa 1880's.
(4.5" square by 7/8" wood box and sixteen 1" diameter by 3/8" painted wood pieces;
paper label on box top and rules on underside of box top;
same box as the one shown on page 25 of the Fifteen book.
"Little Buttercup Puzzle", B. F. Gould, 40 Bromfield St., Boston, 1880.




(cardboard box and 15 wood pieces, 3 by 3 by 1 inch;
the ridged tops have the numbers 1-15 and the smooth bottoms have letters
(close-ups of the piece P / 5 are shown above),
the directions on the box top ask you to spell LITTLEBUTTERCUP
(the fourth T and the C are a too worn to read in the photo above),
the Fifteen book shows this puzzle on pages 20, 36, and 49
where it credits manufacture to B. F. Gould and shows a Feb. 1880 advertisement)



Hopkins, Oxford, NY, circa 1880's.
(wood tray and 15 wood pieces, 3.7 inches;
1 is a bit burned, 5 is damaged, and 10 was lost and replaced by a blank,
the back is stamped "J. A. Hopkins MAKER Oxford NY",
from J. A. Storer's grandfather in Oxford NY)

"The Game of Fifteen Gem Puzzle", manufactured by Alan L. Lovejoy, Boston, 1880.
(cardboard box. wood tray, and 15 wood pieces, 3.75 by 3.75 by 3/4 inches;
shown on page 19 of the Fifteen book where it cites manufacture and date)

"The Game of Fifteen Gem Puzzle", circa 1880.
(cardboard box. wood tray, and 15 wood pieces, 3.75 by 3.75 by 3/4 inches;
shown on page 23 of the Fifteen book)


"Double Puzzle Of Crack Brain And Thirty Four", Heyer Brothers, Boston, circa 1880.
(cardboard box, wood tray, and 16 wood pieces, 3.9 by 3.9 by 3/4 inches;
directions on the inside of the box top;
shown on page 40 of the Fifteen book.


"The Gem Puzzle / Double Puzzle", circa 1880's.
(cardboard box and 16 wood pieces, 3.25 inches square by 9/16 inches;
shown on page 34 of the Fifteen book;
includes piece 16 to have the magic square as a second puzzle)


"The Boston Puzzle", circa 1880's.
(cardboard box and 15 wood pieces, 3 inches square by 5/8 inches;
different than the "Boston Puzzle" shown on page 24 of the Fifteen book)



"The Puzzle Of 15 and 16", circa 1880's.
(cardboard box and 16 wood pieces, 3.25 inches square by 51/2 inches;
shown on page 38 of the Fifteen book;
"This little puzzle looks simple and easy but TRY IT ONCE.";
this one came with an article from a 1926 newspaper that reflects on the Fifteen Puzzle
as something from the past when R. B. Hayes was president)


"The Popular Fifteen Puzzle", F. Passmore, London, circa 1880's.
cardboard box and 15 wood pieces, 4.2 inches square by 5/8 inches;
directions on the inside of the box top;
On page 30 of the Fifteen book, but with a different English manufacture;
a very similar box top is also shown inside the cover of the Fifteen book)


German, circa 1880's.
(cardboard box and wood pieces, 2.5 x 2.5 x 3/8 inches;
shown on page 121 of the Fifteen book)
On the page of the Fifteen book that shows this puzzle is a nice discussion of how newspapers from February and March of 1880 had a large number of "notes, articles, and poems that claimed that the Fifteen Puzzle was driving solvers insane and overcrowding the lunatic asylims".


"15 Puzzle", Spear Works Bavaria 1915.
(cardboard box and wood pieces, 4 x4 x 5/8 inches;
shown on page 119 of the Fifteen book where it cites manufacture and date)




"Gem Puzzle" by John Heywood, Manchester, UK, undated.
(cardboard box and 16 wood pieces, 3.4 x 3.4 x 1/2 inch,
shown on page 29 of the Fifteen book)

"15 and 34" puzzle, De La Rue & Co., London, circa 1880.
(cardboard box. wood tray, and 15 wood pieces, 3.75 by 3.75 by 5/8 inches;
shown on page 35 of the Fifteen book)



"King George VI Coronation Puzzle", circa 1937.
(cardboard box and 16 cardboard pieces, 4.25 x 4.25 x 1/4 inch;
inside of box top has directions;
inside of the box bottom advertises Meadow Butter;
both the puzzle pieces and the box top have photos of the royal family; to read about king George VI, see for example
the King George VI Wikipedia Page,
from: http://en.wikipedia.org/wiki/King_George_VI )

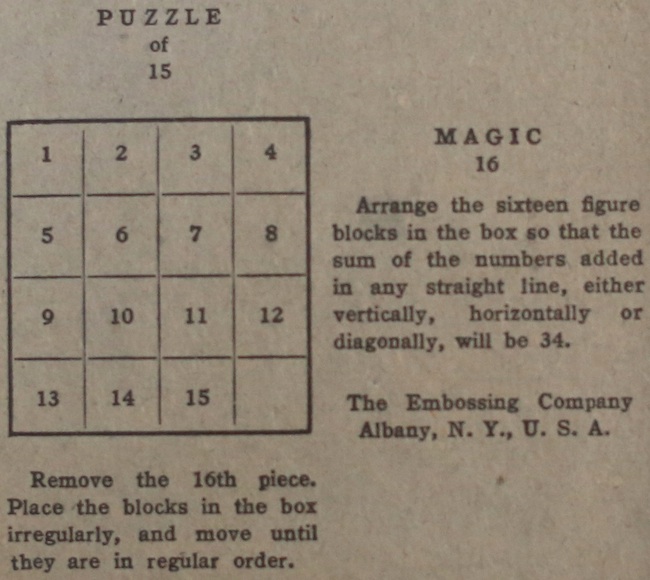
Magic 16 Puzzle", Copyright The Embossing Company, Albany, NY, 1930.
(3.3" x 3.3" x 9/16", sixteen 3/4" square by 1/2" thick wood pieces)




"15 Puzzle", The Embossing Company, Albany, NY, circa 1937.
cardboard box and 15 wood pieces, 4.2 x 4.2 x 5/8 inch;
this red version appears to have a second 6 instead of a 9,
same manufacturer and box size / style as the Time and Missionary Puzzles)




"The Combination Puzzling Puzzles", copyright Canada 1934.
(wood box, 15 wood pieces, 3.9 by 3.9 by 7/8 inches;
flip the puzzle over and the backs of the pieces have the letters GDOAETYNANALNI?,
? for piece 13 that has been replaced and had A hand written on the back)


Adams Co., unknown age.
(cardboard case and metal puzzle, 3.25 inches)

101 Dalmatians, Disney, circa 1960's?
(plastic, 3.5" x 3")

Donald Duck, Walt Disney Productions,
(plastic, 2+5/8" x 2+5/8" x 3/16")

Santa Claus, circa 2000?
(plastic, 2+3/4" x 4.5" x 3/16")
Wikipedia Fifteen Page, from: http://en.wikipedia.org/wiki/Fifteen_puzzle
Slocum's Page, from: http://www.puzzleworld.org/PuzzleWorld/jerry_slocum.htm
Baxter's Page, from: http://www.johnrausch.com/SlidingBlockPuzzles/15.htm
Jaap's Page, from: http://www.jaapsch.net/puzzles/fifteen.htm
Casselman's Page, from: https://personal.math.ubc.ca/~cass/courses/m308-02b/projects/grant/fifteen.html
Wikipedia Magic Square Page, from: http://en.wikipedia.org/wiki/Magic_square
Wolfram Magic Square Page, from: http://mathworld.wolfram.com/MagicSquare.html
May Patent, from: www.uspto.gov - patent no. 50,608
Kinsey Patent, from: www.uspto.gov - patent no. 207,124
McCleary Patent, from: www.uspto.gov - patent no. 284,037
Brown Patent, from: www.uspto.gov - patent no. 390,829
Bradshaw Patent, from: www.uspto.gov - patent no. 427,392
Brown Patent, from: www.uspto.gov - patent no. 433,444
Cook Patent, from: www.uspto.gov - patent no. 476,980
Anderson Patent, from: www.uspto.gov - patent no. 483,276
Eymann Patent, from: www.uspto.gov - patent no. 535,279
Johnson Patent, from: www.uspto.gov - patent no. 1,555,980
Fritz Patent, from: www.uspto.gov - patent no. 1,693,711
Nesis Patent, from: www.uspto.gov - patent no. 5,785,318
Examples of Roalex Puzzles For Sale

Roalex Co., Forest Hills, NJ, circa 1950's and 1960's.
(card is 4.4 by 5.75 inches, puzzle is plastic 2.5 inches by 1/4 inch thick;
the spacing of the copyright information at the bottom varies on some cards)
M. Keith discusses this puzzle and gives the solution shown in the photo above as well as a number of other sentences like "YAMS GROW BUT HIDE" and phrases like "DEAR BOYS WITH GUM" (M. Keith [2011], "Vintage Plastic Sliding-Letter Puzzles" Word Ways 44:4, 310-31; see also M. Keith [2012], "More Sliding-Letter Puzzles"). C. Bates has also found the sentence "I SAW THEM BURY GOD".





Copyright 1946 Goetze Games Co., Plymouth Wis.
(folding cardboard box and 15 wood pieces, 6.3" x 6.3" x 5/8";
the classic Fifteen puzzle with specific start / end position problems)



The Embossing Company, Albany, NY, circa 1930's.
(4.4"x4.4"x5/8" inch cardboard box and 16 wood pieces; directions inside box top)

a.k.a. Fifteen Puzzle
Basic idea dates to before 1900, this Escher drawing purchased 2007.
(plastic, 3.6 by 2.9 inches)
Like the Fifteen puzzle puzzle except there are sixteen pieces and a seventeenth extra space. The piece adjacent to the extra space in the solved position will always either be there (in which case no pieces can move until it is moved into the extra space) or be in the extra space. So this puzzle can be solved by first placing this piece in the extra space, solving the remaining Fifteen puzzle, and then moving this piece back. The position of the extra space does not matter, and varies from one puzzle to another. Here's one with the extra square by the upper right corner:

Flintstones, circa 1965?
(plastic, 3.6 by 2.9 inches)
Further reading:
Larabee Patent, from: www.uspto.gov - patent no. 1,477,371
Green Patent, from: www.uspto.gov - patent no. 2.007.530
Feller Patent, from: www.uspto.gov - patent no. 5,529,301

a.k.a. a.k.a. 5-Block Puzzle, Lodging House Difficulty
Very old design, this one made by J. A. Storer 2007.
(cardboard sleeve, 5 by 7 by 3/4 inch wood tray, and five wood pieces)
The problem is to exchange pieces A and B by sliding the pieces::
Presented in the 1914 Loyd book; both the 1942 Filipiak book and the Hordern book present a 17 moves solution (and Baxter's Page lets you play it on-line):
Further Reading
Baxter's Page, from: http://www.johnrausch.com/SlidingBlockPuzzles/classic.htm


a.k.a. Super Solitaire
"Super Solitaire", Roalex Co., Forest Hills, NJ, circa 1950's and 1960's.
(puzzle is held by sleeve in back and not glued to the card;
card is 5+1/4" x 4+1/8",
puzzle excluding the keychain loop is plastic 1+3/8" x 2+3/8" by 7/32")
Since the Fifteen puzzle can be solved by easily arranging the first two rows and then solving the last two rows, this puzzle captures most of its (limited) complexity.
A smaller version of the Fifteen Puzzle. Although relatively easy, graphics on the pieces tend to make solving more difficult than if the pieces were the numbers 1 through 8.

Superman
Copyright National Periodical Publications, 1966.
(plastic, 9" square by 3/8" thick)





Tweety Bird
Back reads: TM & C 1997 Warner Bros. DaMert Company Berkeley CA Made in China.
Card back reads: Copyright DaMert Company, Berkeley CA, 1997.
(plastic with raised graphics, 4" square by 1/4" thick tray, on an 8" x 5.5" cardboard card;
taking into account the raised graphics the puzzle is 3/4" thick;")


Gecko
Back reads: C 1993 DaMert Company San Leandro, CA Made in China Patent Pending
(plastic with raised graphics, 4" square by 1/4" thick tray;
taking into account the raised graphics the puzzle is 3/4" thick;")
The copyright shown on the back of this puzzle (photo above) is 1993, 4 years earlier that the Tweety version, and shows the patent pending. DaMert made a number of these sliding puzzles all the same size, where some had copyrights in the intervening time, such as the Turtle puzzle (copyright DaMert 1994, San Leandro, CA) and the Earth-Moon puzzle (copyright DaMert 1996, Berkeley, CA).


Alien
Back reads: C 1993 DaMert Company Berkeley, CA Made in China Patent Pending
(plastic with raised graphics, 4" square by 1/4" thick tray;
taking into account the raised graphics the puzzle is 3/4" thick;")
The copyright shown on the back of this puzzle (photo above) is 1993; same as the Gecko puzzle of the previous page except that the company listed is Berkeley, CA.

Praying Mantis.
(plastic with raised graphics, 3 inches)

Lisa Simpson.
(plastic, 1.9 inches)
Maggie Simpson.
(plastic, 1.9 inches)



Copyright Richard Appel, Inc., NY, 1943.
(2.5"x2.5"x1" cardboard box, 2.4" square board, and eight 13/16" wood cubes;
Described on pages 135-136 of the Hordern book, which dates the puzzle)
Start with the cubes placed on the board according to their color, and then move the purple cube in the upper left corner to the lower right corner in such a way that pieces of the same color never touch each other along a side. The two purple blocks may not touch, but are different shades of purple allow one to keep track of which is the one that started in the upper left.Includes a 24 move solution; Hordern presents a minimal 22 move solution:


G Y O Y G P Y O P G O G O Y G P Y O P G Y P
Figure from the 1985 Morrone Patent U.S. 4,548,410.
The Morrone patent (Fig. 3 shown above) shows a version of the Nine Puzzle where instead of a missing square there are 9 pieces and an extra tenth position into which one can be slid so the others can move around like the standard Nine Puzzle; the patent also shown an object of the puzzle to arrange the pieces so that the numbers add to 15 in all directions. Below is an add for Phenyo Caffein which was found tucked into the pages of the green cover version of the 1893 Hoffman book. It presents a 3x3 magic square puzzle. This puzzle is also shown on the back of the Phenyo Caffein solution to the Misfit Puzzle, and Phenyo Caffein also provides a version of the Sectional Checkboard Puzzle.


Further reading:
See also the The Great Fifty Puzzle for 4x4 Magic Squares.
Morrone Patent, from: www.uspto.gov - patent no. 4,548,410
Wikipedia Page, from: http://en.wikipedia.org/wiki/Magic_square


Craig Biscuit Co., Fort Wayne, Indiana, unknown age.
(cardboard box 4" by 4" by 1/2" and 16 wood pieces)
Make a 4x4 magic square where all rows, columns, and diagonals add to 34. This is in a theme similar to many versions of the Fifteen puzzle that include a 16th square so that one can make a magic square, as show above on the right.
Further Reading
See also the Double Puzzle Of Crack Brain And Thirty Four version of the Fifteen puzzle.
See also the Magic Square Puzzle 3x3...
Wikipedia Magic Square Page, from: http://en.wikipedia.org/wiki/Magic_square
Wolfram Magic Square Page, from: http://mathworld.wolfram.com/MagicSquare.html




Copyright S. S. A. Co., 1915.
(1.75"x4.75"x7/16" cardboard box and 12 wood pieces with paper glued to top;
directions are on the inside of the box lid)
Starting with the P and C exchanged, slide the pieces to put them back.
A parity argument (like that for the Fifteen puzzle) might lead one to think that a solution is not possible. However, the second and fourth squares of PANAMA can be exchanged without significantly changing the look of the picture formed by the pieces (if one ignores the background graphics, then shorter solutions are possible - see next page).
Panama Canal: Here is a 32 move solution, where 1, 2, 3, 4, 5 represent the five A's, and X, Y represent the two N's. If a piece can push other pieces, then this solution can be converted to 21 moves by combining steps 1/2, 8/9/10, 12/13/14, 16/17, 21/22, 28/29/30/31/32.
Panama Canal NB: For the simpler problem with no background, here is a 26 move solution. If a piece can push other pieces, then this solution can be converted to 17 moves by combining steps 1/2/3/4, 8/9, 15/16, 22/23/24/25/26.
Panama Canal H: For the even simpler problem with no background and "CANAL" can be right justified, Hordern's book gives a 23 move solution and Baxter's Page lets one search for a 21 move solution. If a piece can push other pieces, then this solution can be converted to 16 moves by combining steps 1/2/3/4, 8/9, 15/16.

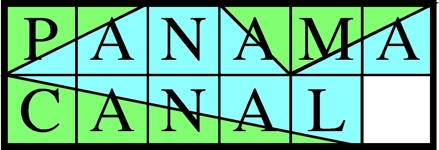
Designed and made by J. A. Storer 2007.
(3"x 7" x 1.4" wood box, 11 wood pieces, and a black wood keeper piece)
Panama Canal S: In this version, the second and sixth squares of PANAMA can be exchanged without changing the picture. Here is a 48 move solution. If a piece can push other pieces, then this solution cab be converted to 36 moves by combining steps 6/7, 11/12, 16/17/18, 20/21/22, 24/25, 29/30, 36/37/38/39, 43/44.
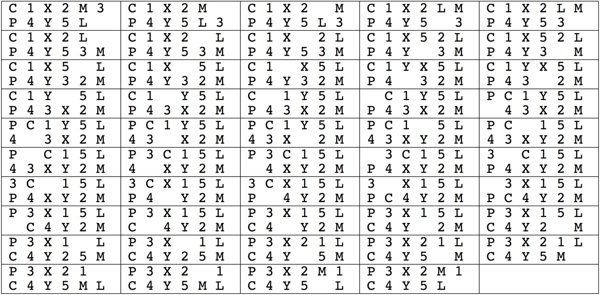
This version does a reasonable job of "exercising" the pieces. Since half of the possible positions are duplicates due to the two A's with the same background, there are 12! / 2 = 239,500,800 distinct positions. To find a solution, a computer program performing a simple breadth-first search visited 102,714,408 positions (43 percent). In contrast, the program visited 3,611,235 positions (1.5 percent) to solve the standard version, and for the NB and H versions, where the five A's are interchangeable and the two N's are interchangeable, giving 12! / 5! / 2 = 3,991,680 distinct positions, to find a solution it visited 120,542 positions (3 percent) and 42,602 positions (1 percent) respectively.
The 2-unit high shape has been used in similar puzzles. The 1923 Hartman patent shows the same puzzle but with the numbers 1 to 11 on the pieces (and the goal is to rearrange them so each column sums to 11). The puzzle below, purchased in 2008, has a 2 by 7 array of pieces and an extra position (similar to the Sixteen puzzle):

Further Reading
Baxter's Page, from: http://www.johnrausch.com/SlidingBlockPuzzles/classic.htm
Hartman Patent, from: www.uspto.gov - patent no. 1,464,424

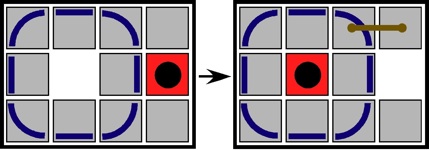
a.k.a. Bullseye, Target, Zot
Very old design, this one made by J. A. Storer 2007.
(wood box 3.5 by 6.5 by 1.25 inches, 11 wood pieces, and a brass clip;
shown on page 8 of the 1942 Filipiak book)
Move the red square to the middle by sliding the pieces. Hordern's book speculates that this puzzle may have began as a mistake when attempting to make the Get My Goat puzzle; it is the same except that the upper right corner is two pieces instead of a single piece (this version allows one to join these two pieces with a brass clip if one wants to play Get My Goat). Hordern's optimal solution of 17 steps shown below (along with an 18th step to adjust the final position) does not need to use the left column.




Skor-Mor Co., 1107 E. Kimberly Ave., Anaheim, CA
top:"FUN FOR ALL AGES / Made Of Hardwood
sides: "ZOT Puzzle"
bottom: "SKOR-MOR CORP./ 1107 E. KIMBERLY AVE. ANAHEIM CALIF. 92801 / EE17"
(cardboard box and 12 wood pieces, 5.25" x 4" x 1/2")



Peterson Games, 1972
(cardboard box with 12 wood pieces, 6.25" x 6.25" x 1/2")
Pieces are the same as for the Skor-Mor version, each 1.25" x 1.25" x 1/2". The box says:top: "ZOT! Peterson Games / c 1972"
left side: "Peterson Puzzles and games are designed primarily for adults and teenagers, however, they are both educational and challenging for children as young as nine years old."
right side: "Stimulate someone's imagination with a Peterson Puzzle or Game"
bottom: "ZOT! Peterson Games / NO. 111"

These directions have ? ? ? in the top row of the finish position, perhaps to encourage one to wonder whether the puzzle can be solved with Z and T ending in their original positions. The Hordern solution uses 17 moves to leave T at the upper left and Z at the upper middle, and an eighteenth move to move Z to the upper right, and makes no use of the last row. However, there is no way to solve the puzzle ending with Z and T in their original positions. On the other hand, if the large circle graphics are ignored and the problem is just to move the dot from the top middle to the third row middle, the puzzle can be solved in 10 moves with the Z and T ending in their original positions (again making no use of the last row). Note that, even ignoring the large circle graphics, it still takes 18 moves to end with T at the upper left and Z at the upper right.

Made 1919.
(cardboard box and 11 stone pieces, 2.6 by 3.3 by 7/16 inches)
Below are the directions that came with the puzzle. Hordern's book dates this puzzle, and gives solutions of 27 moves to get the three discs to the center and 28 moves to get them to the bottom (with GOOD LUCK on the first two rows).



a.k.a. Fourteen Puzzle
PLAS TRIX CO., Brooklyn, NY, 1950.
(soft plastic case, cards, and two 2.5 by 3.75 inch puzzles)
Similar to the Fifteen puzzle; use one puzzle to try to make different patterns (e.g., 1 to 14 in numerical order), or two puzzles to race an opponent to make patterns specified by the playing cards. Here are the front of the card box, the back of each playing card, the text from the back of the card box, and the front and back of the instructions card:






Circa 1960's?
(plastic, 20 tiles, 3.4" by 1.5" by 1/4" thick)
Larger version of the Nine Puzzle; can be solved in the same way.




The Embossing Company, Albany, NY, circa 1930;s.
(cardboard box 4.1" x 4.1" x 1/2" and 24 wood 3/4" x 3/4" x 3/8" wood pieces)
A 5 x 5 version of the Fifteen puzzle. Begin with the orange lettering up, solve the crossword puzzle on the orange side of the directions, and slide the pieces to make that pattern. Then turn over the pieces to have the green lettering up, turn the directions over to green side, solve that crossword puzzle, and slide the pieces to make that pattern. On the right above is each piece of the orange solution turned over.
A larger version of the Fifteen puzzle that can be solved the same way; (see also the 31 and 49 puzzles).

Unknown manufacture.
(wood, 3 by 4.75 by 1.25 inches)
The box can be turned over to play the One To Ten on the other side:


Circa 1960?
(plastic, 27 tiles, 4.7 by 2.9 by 3/16 inch thick)
Circa 1960?



(plastic, 27 tiles, 4 by 2.4 by 3/16 inches)


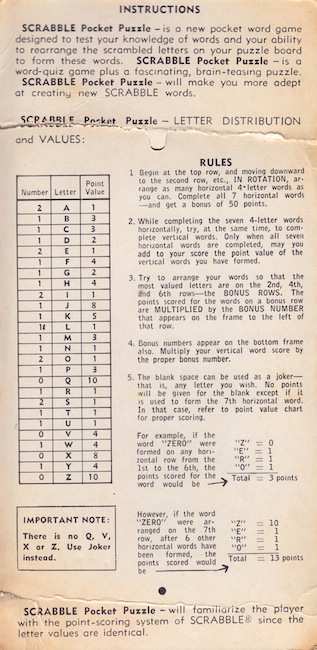
Copyright Plas-Trix Co. 1954, "under license by the makers of SCRABBLE".
(plastic, 4.9" x 3.1" x 3/16")

Requires one to work out a crossword puzzle, Plastrix Co., circa 1950's.
(9" x 7" cardboard card and plastic puzzle 4.9" x 3.1" x 5/16"; solution above from
M. Keith [2011], "Vintage Plastic Sliding-Letter Puzzles" Word Ways 44:4, 310-31; see also M. Keith [2012], "More Sliding-Letter Puzzles").


a.k.a. Jumble, TWIDL
Archer Plastics, Bronx, NY, circa 1960.
(plastic, 31 tiles, 5 by 2.9 by 1/4 inch thick)
A larger version of the Fifteen puzzle that can be solved the same way (see also the 27 and 49 puzzles).


Wm. F. Drueke & Sons, Grand Rapids, Mich.", circa 1960's.
(plastic, 31 tiles, 5.1 by 2.9 by 1/4 inch thick)
Map of the U.S., circa 2000?
(plastic, 31 tiles, 3 by 5 by 3/16 inches)
Puzzles of individual states have also been made (e.g. Oklahoma).

"Roalex's Zig-Zaw Puzzle Map of The World", circa 1960s.
(plastic, 31 tiles, 3 by 5 by 5/16 inches)


Wm.F. Drueke & Sons, Grand Rapids, 4, Mich.
(plastic puzzle with 31 tiles 2.9" x 5.1" x 1/4"; directions on the back)
With a computer in 2011, M. Keith identified 299 solutions using valid Scrabble words with the stronger requirement of having no two-letter words; 14 of them use only the first 7 columns (M. Keith [2011], "Vintage Plastic Sliding-Letter Puzzles" Word Ways 44:4, 310-31; see also M. Keith [2012], "More Sliding-Letter Puzzles").

Roalex Co., Forest Hills, NJ, circa 1960's.
(plastic puzzle with 31 tiles on a cardboard card, 5.5" x 7.5")
A detailed analysis of this puzzle (that concludes by liking the solution shown above) is presented by (M. Keith [2011], "Vintage Plastic Sliding-Letter Puzzles" Word Ways 44:4, 310-31; see also M. Keith [2012], "More Sliding-Letter Puzzles").

Roalex Co., Forest Hills, NJ, circa 1960's.
(plastic puzzle with 31 tiles on a cardboard card, 5.25" x 8.5")
Advertising for this puzzle called it "beautiful and Durable, dark color plastic frame with thirty-one E-Z moving squares".



Copyright DC Comics 1993.
(plastic, 6" x 4+78" x 1/4")
A larger version of the Fifteen puzzle in a 7x7 array that can be solved the same way (see also the 27 and 31 puzzles). The only difference is that, like the Sixteen puzzle, the keeper piece is in an extra space, where the piece adjacent to the extra space in the solved position will always either be there (in which case no pieces can move until it is moved into the extra space) or be in the extra space, and so solving can first place this piece in the extra space, solve the remaining 48 positions puzzle, and then move this piece back.


Roalex Co., Forest Hills, NJ, Version 1 circa 1950's and Version 2 circa 1960's.
(Version 1 - 3" x 8" x 7/17" puzzle on 5.25" x 10.25" card,
Version 2 - 2+13/16" x 8+1/"8 x 1/4" puzzle on 5+3/8" x 10.5" card)
Mike Keith in his 2011 article (M. Keith [2011], "Vintage Plastic Sliding-Letter Puzzles"; Word Ways 44:4, 310-31; see also M. Keith [2012], "More Sliding-Letter Puzzles") discusses this puzzle, presents solutions that have a single long word per line, and other fun activities with this puzzle, including writing a short story constrained by the puzzle.

The writing is faded and hard to read; here is what is there:

Mike Keith has pointed out that although the "solution" on the right is wrong (it has one too many of A,C,T, and leaves one two few of I,N,G), the second CAT could be replaced by GIN to make a legal solution:


a.k.a. Slide-Blocked Sliding Block
Designed by B. Cutler 1988, made by T. Lensch 2007.
(laser engraved wood, 7.5 by 5.5 by 3/4 inches)
The 5 unit size blocks slide in the tray and can't be removed due to interlocking edges. The edges are formed in a way that not all sliding motions are possible at any given time. The goal is to move Grandpa's car from the right to the left. The edges are such that the left door top / window bottom cannot slide above the car, and hence the middle two squares must be exchanged. By the same parity argument as for the Fifteen Puzzle Puzzle, this implies that the top two squares must also be exchanged. Hence, the puzzle is:
This puzzle is bit harder than the Moving Day puzzle but not too hard. The sheet that was sold with the puzzle gives the following solution of 41 moves; here we use a letter to denote moving the corresponding piece and a number to repeat the group in parentheses that many times:
(Y X A B G)3 Y B A X B Y G A Y B X Y A G B A (G B A X Y)2



Patented by T. Graham 1934, made by the Embossing Company of Albany 1937.
(cardboard box 4.4" x 4.4" x 5/8" inches and 13 wood pieces;
Hordern's book dates the blue version above as made in 1937, and gives a solution)
Slide the pieces, avoiding the two forbidden squares, to get go from a start position to a final position; here are problems 1, 2, and 3 from the directions that were sold with it:





Copyright 1942, Lowe Bookshelf Games, New York, NY.
(cardboard case, 4.6" x 4.6" x 7/8"; was also made with a red case)
Further Reading
Graham 1934 Design Patent, from: www.uspto.gov - patent no. Des93,344
Graham 1935 Patent, from: www.uspto.gov - patent no. 1,989,411

a.k.a. Motor Garage Puzzle, Parka Car, Sputnik Puzzle, E Peg Puzzle
Designed by H. E. Dudeney 1910, made by Binary Arts circa 2000.
(metal with plastic case, 2.5 inches)
Slide the pieces to exchange "WORK" and "GOLF":
Presented in Dudney's 1917 book Amusements in Mathematics as the Motor Garage Puzzle, which also presents the smaller Motor Car Puzzle. Hordern's book credits Dudney's 1910 submission to the Strand Magazine. Here is the 43 moves (85 straight-line moves) solution from page 27 of the 1942 Filipiak book (steps 6 and 7 have been corrected and letters are used instead of numbers to the left of arrows):
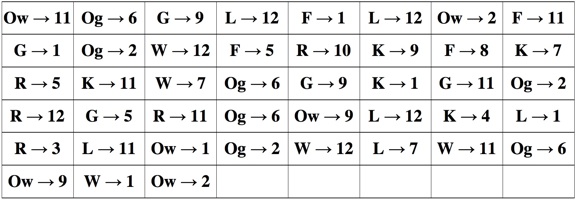
Further Reading
DeVos Patent, from: www.uspto.gov - patent no. 4,097,049

a.k.a. Black And White
Copyright Binray Arts 2002.
(originally "BLACK and WHITE" by K. Wells, Popular Mech. 1971; metal 1.75" x 3")
Here are every 6th step of a 42 rectilinear (57 straight-line) moves solution (note that the two O's of HONOR get exchanged in the process).
Here are every 8th step of a 56 rectilinear (74 straight-line) moves solution for the harder puzzle where every square is unique (as would be the case if the words were BLACK and WHITE); the second O of honor is represented by a Q (a 72 straight line moves solution is also possibe).
Here are every 6th step plus the final step of a 37 rectilinear (50 straight-line) moves solution for the easier puzzle when all three O's are interchangeable and the two R's are interchangeable:
Hordern's book Hordern's book gives a 62 rectilinear moves (85 straight-line moves) solution for the BLACK and WHITE version; starting with HONOR on top and GLORY on the bottom, with each tile made uniqueue by labeling it also with the corresponding letters from black and white, here are the positions resulting from the 23 non-straight-line moves, and the final position:


Designed by S. Gabarchuk, made by D. Namdarian, 2011, sleeve made by J. A. Storer.
(laser cut plastic, 4.8" x 5.9" inches)
As shown on the puzzle sleeve above, start with a pattern with a ball on the left and slide the pieces to form a symmetric pattern with a ball on the right. All the pieces have a square bottom layer that can pass under the curve rims at the corners. The three blank blue pieces can move anywhere, but the other pieces have a red or yellow shape on the top layer that prevents them from moving into some corners. Without the curved corner rims, the puzzle could be solved in 34 moves, but as is, 36 moves are needed:




Made in Russia, circa 1980's.
(plastic, 4.2 x 1.8 x 5/16 inches; was also sold with a green body)
From the directions figures, this puzzle is seen to be equivalent to the Towers of Hanoi Puzzle, where the tiles must be moved from the first to the third column in such a way that a tile is never above a lower numbered one.


a.k.a. Ride or Walk
Design, copyright, and 3D print by J. A. Storer, 2022.
(plastic, 3 x 4 x 3/8 inches, with cardboard sleeve)
Two simple puzzles in one. The easier version is to remove the two keepers and the s, and then slide the pieces to exchange Nite and Day; it can be done in 30 rectilinear moves. The harder version keeps the s and can be done in 58 rectilinear moves.

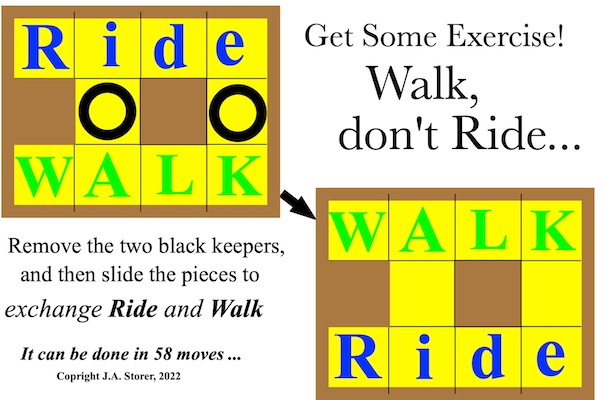
a.k.a. Nite and Days
Design, copyright, and 3D print by J. A. Storer, 2022.
(plastic, 3 x 4 x 3/8 inches, with cardboard sleeve)
Same puzzle as Nite and Days Remove the two keepers and then slide the pieces to exchange Ride and Walk; it can be done in 58 rectilinear moves.

a.k.a. Nite and Days, Ride or Walk
Copyright J. Andrew Storer, 2022. Made by J. Alexander Storer, 2022
(plastic, 3 x 4 x 3/8 inches, with cardboard sleeve)
Same puzzle as Nite and Days and Ride or Walk Remove the two circle keepers and then slide the pieces to exchange the light colored and dark colored pieces (keeping the order 1234); it can be done in 58 rectilinear moves.
Crafted from multiple woods:Tray and keepers: Leopard Wood
Light pieces: Morodo
Dark Pieces: Bocote
Pegs: Birch dowel

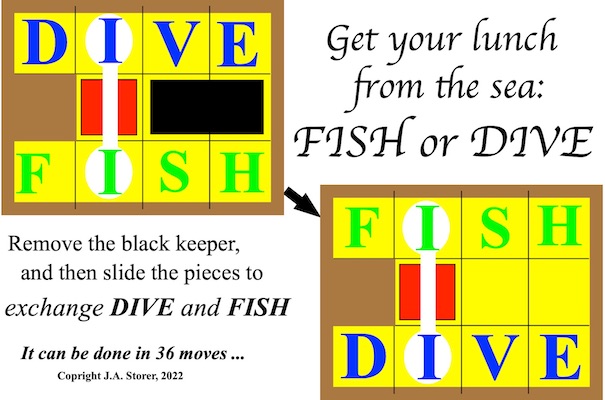
Design, copyright, and 3D print by J. A. Storer, 2022.
(plastic, 3 x 4 x 3/8 inches, with cardboard sleeve)
Remove the black keeper and then slide the pieces to exchange DIVE and FISH; it can be done in 36 rectilinear moves. Motivated by the small size of the Ride or Walk puzzle and the "bridge" of the Work or Golf Abridged puzzle, this puzzle has a single fixed square, a free moving square, and the two I's are connected (forcing them to move only left and right in lock-step).

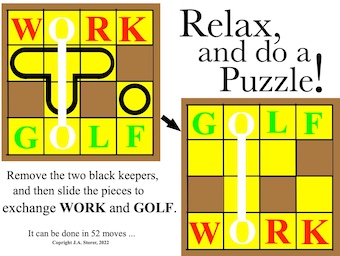
Design, copyright, and 3D print by J. A. Storer, 2022.
(plastic, 4 x 4 x 3/8 inches, with cardboard sleeve)
Inspired by the classic Work or Golf puzzle (which is based on a 5 x 4 grid), this puzzle is based on an "abridged" 4x4 grid where a "bridge" connects the O's (and forces them to move only left and right in lock-step). It can be done in 52 rectilinear moves.
Other words can be used to make effectively the same puzzle, so long as the second tiles on the top and bottom are the same. Using different colors, top and bottom words can have a letter in common (e.g. Cake and Bake). More than one letter on a tile is possible (e.g. M - A - R - S in G - A - LA - XY has a double character in the bottom two rightmost positions and WI - NI - N - G and DI - NI - N - G has a double character in the first two positions of both the top and bottom). Graphics could also be used instead of letters, such as a heart for L in ILNY (I Love New York).


a.k.a. Katch the Kaiser, Katch The Kron Prinz, ...
Patented by J. Wiley 1914.
(left: 2.9" x 3.75" x 7/16" cardboard box and 11 wood pieces 1/4" thick;
right: 2.9 by 3.75 by 3/8 inch cardboard box and 11 cardboard pieces 3/16" thick;
both box tops say "OFFICE 1058 BROAD ST. PROV. R.I. PAT. OCT. 6, 1914";
solution sheet of the red version says "Rust Craft Publishers, Inc., Boston, MA.";
shown on plate 6 of Hordern's book and page 134 of the Fifteen book;
similar to but a bit harder than the Bull's-Eye puzzle)
There are one 1x2 piece (in the upper right of the starting position), nine 1x1 pieces, and 1 keeper piece (center of the starting position). Both box tops have the same directions on the underside, that instruct one to move the goat to the middle:



Inlaid Company, Providence, R.I., patented October 6, 1914.
(2.9" x 3.75" x 3/8" cardboard box and 11 cardboard pieces 3/16" thick)


"BRITISH MADE, Patent No. 14356/16 Appd. for."
(2.9" x 3.75" x 3/8" inch cardboard box and 11 cardboard pieces 3/16" thick)

"Created by Zen", Bridgeport, CT, Copyright 1942.
(3.4" x 4.4" x 7/16" cardboard box with raised bottom and 11 cardboard pieces 1/8" thick)
Further Reading
Baxter's's Page, from: http://www.johnrausch.com/SlidingBlockPuzzles/classic.htm
Wiley Patent, from: www.uspto.gov - patent no. 1,112,746


The Embossing Company, Albany, NY, 1934.
(cardboard box 3.5 by 5.4 by 1/2 inches, 2 styles shown above, and ten wood pieces;
described on page 70 of the Hordern book, where it is dated and
credited as named to celebrate the birth of the Dionne quintuplets;
same manufacturer and box style as the Fifteen, Time, and Missionary Puzzles)
Line up the Quinties in the center row from the specified starting position; the directions are shown on the next page; here are diagrams of positions 0, 4, 8, 12, 16, 20, 25, 30 of the Hordern book solution of 30 rectilinear moves (equal to 33 straight-line moves):



Southern Toy Co. for Long Sales Co., Johnson City, TN, circa 1930's?
(wood box that looks like a book and 7 wood pieces, 8.5" x 6" x 5/8")
Exchange the dark and light pieces; here are selected positions of a not minimal 42 rectilinear moves solution (59 straight-line moves):
Starting with move 15 of the solution of the previous page (step 5 of the selected steps shown), here are different additional steps that can be taken to achieve a 39 rectilinear moves solution:
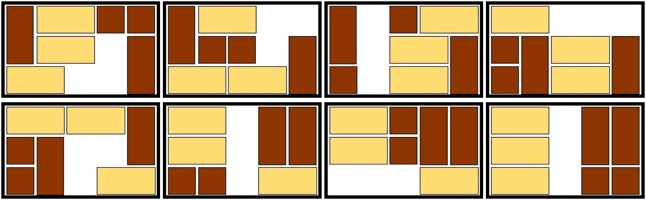
Here is the full 39 moves rectilinear move solution (59 straight-line moves):
Here is a 58 straight-line moves solution (41 rectilinear moves):

Designed by Serhiy Grabarchuk, made by J. A. Storer 2007.
(4" x 4" x 3/4" wood tray, 7 wood pieces, and black plexiglass keeper)
Move all the pieces clockwise one unit:
Baxter's Page lets you play this puzzle on-line to try to find the 31 move minimal length solution.
Further Reading
Baxter's Page, from: http://www.johnrausch.com/SlidingBlockPuzzles/serhiy.htm

Designed by Serhiy and Peter Gabarchuk, made by D. Namdarian, 2012.
(3 layers of laser cut plastic, 2.5" x 3+1/8" x 5/16", with directions that show two problems)
Here are 26 rectilinear (28 straight-line) moves and 20 rectilinear (22 straight-line) moves solutions for the two problems, as well as a 24 rectilinear (24 straight-line) move solution to go between the two solved positions (24 rectilinear moves, using 26 straight-line moves, suffice if X and Y are exchanged):

Copyright S. Grabarchuk, made by D. Namdarian 2012; sleeve made by J. A. Storer.


(plastic, 4+3/8" x 5+9/16" x 3/8";
2 layer base, 1 layer pieces and rim, each layer 1/8" thick)
Here is a solution of 33 moves:
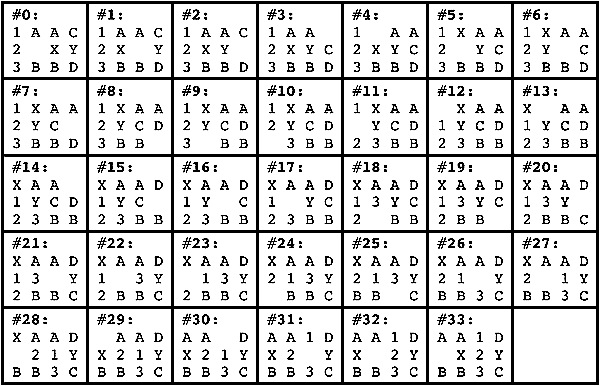
These were a series of cardboard puzzles (see the following pages for examples) that came in a fold-out mail envelope; presumably an inexpensive amusement that could be mailed to a friend or family member. They are based on 1x1 and 1x2 pieces on a 3 x 5 unit board. For example, here is the problem of the "Tank Attack" puzzle (shown on the next page):
The instructions for Tank Attack, like other puzzles in the series, show a filler piece no. 1 for the 2 x 1 empty space, call it a move to remove this piece and replace it at the end, and give a solution of 24 straight-line moves that includes these two moves. However, this solution is referred to as 22 moves. So we won't count those two extra moves her either. Also like other puzzles in the series, the instructions for Tank Attack pose the simpler problem of moving piece 4 to the lower right without regard to where the other pieces end up. Here is a 13 straight-line move solution to do that (or 11 rectilinear moves by combining steps 1 and 2 and combining steps 4 and 5); in the steps below, 0 denotes piece 10:







Electric Corporation Of America, Chicago, Copyright 1942.
(paper envelope and cardboard puzzle, 4.4" x 6.3")







Electric Corporation Of America, Chicago, Copyright 1942.
(paper envelope and cardboard puzzle, 4.4" x 6.3")







Electric Corporation Of America, Chicago, Copyright 1942.
(paper envelope and cardboard puzzle, 4.4" x 6.3")

Designed by Stewart Coffin 2005; this one made by J. A. Storer 2011.
(Walnut and Cherry with paper piece labels, 4" x 4" x 3/4")
Slide the pieces to fix the caterpillar and butterfly. Below are every 5th move of a 39 rectilinear (51 straight-line) moves solution. Solving for the order caterpillar - butterfly - Monarch can also be done in 39 rectilinear (50 straight-line) moves, and 39 rectilinear (51 straight-line) moves suffice to go between these two solutions.


Designed and made by D. Namdarian 2013; sleeve added by J. Storer.
(3 layers laser cut plastic, 4.75" x 4.74" x 3/8")
Legal chess moves are not always possible (e.g., consider the 1x2 piece with the white bishop for which a diagonal move would require at least 3 blank squares). However, here is a 36 rectilinear (40 straight-line) moves solution using normal sliding:


Copyright ThinkFun 2009.
(plastic, 3.2" x 3.2" x 1")
The object is to slide the arrow out the hole in the bottom. The rectangle is sufficiently large to allow the pieces to be slide in a non-rectilinear fashion to the position shown below, after which further sliding moves the arrow out.





a.k.a. Dad's Puzzle, Moving Puzzle, Tit-Bits Teaser No. 1,
Penant Puzzle, Box of Nine, Nine Block Puzzle
Patents and copyrights include L. W. Hardy 1909, J. W. Hayward 1926,
Frederic E. Aaron 1927, and C. O. Luce 1953, these two are not dated.
(cardboard box and 9 wood pieces, 4 by 3.25 by 1/2 inches;
presented on pages 78-79 and plate 6 of Hordern's book)
Slide the 2x2 piece from the upper left to the lower left (without picking up pieces); the positions of the other pieces don't matter:Perhaps the most produced mechanical puzzle of the first half of the 20th century, after the Fifteen puzzle. Many were made with the same 4 x 3.25 x 1/2 inch box, the same size and shaped pieces (sometimes plastic in later years), but with additional text or different cover art to promote products (laundry detergent, glue, etc.). See also the Humdinger version.
Here is a solution of 62 straight-line moves; it can be converted to 59 rectilinear moves by combining steps 6/7, 27/28, and 58/59:

(one move = sliding one piece any number of units in one direction)
The diagonal version of Dad's Puzzler is to move the 2x2 piece diagonally to the lower right corner; it is described on page 5 of the 1942 Filipiak book (which gives a solution of 59 moves).
(Move the 2x2 to the lower right; the positions of the other pieces do not matter.)
One might think that it would be a harder to move the 2x2 piece diagonally to the lower right corner since it is farther away than the lower left. However, here is a solution of only 31 straight-line moves; it can be converted to 29 rectilinear moves by combining steps 6/7 and 18/19:
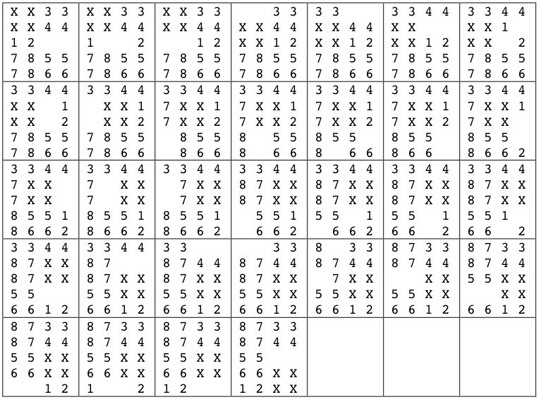
(one move = sliding one piece any number of units in one direction)
Note: For harder versions of Dad's Puzzler where there are additional constraints on the final position, see Dad's Puzzler Exchange.



Pennant Puzzle, circa 1910.
(cardboard box, 9 cardboard pieces, 4.1 by 3.3 by 1/4 inches)
Often credited as the first version made of Dad's puzzler. A slightly different manufacture of this puzzle has the same box top except at the bottom it says "PATENT ALLOWED DIRECTIONS ON BOTTOM OF BOX" and does not credit Hardy 1909, the same directions except the address for O. K. Novelty of Chicago is listed as "225 North Sangamon St.", and the same baseball teams on the pieces, which are more of an off-white color.


Tit-Bits Teaser, George Newnes, London, Made in the U.S.A., 1927.
(cardboard box, 9 wood pieces, 4 by 3.25 by 1/2 inches;
page 78 of Hordern's book list this as "Tit-Bits Teaser No. 1, 1927")
Moving Puzzle, Copyright Frederick E. Aaron 1927.




(cardboard box, 9 wood pieces, and solution sheet, 4 by 3.25 by 1/2 inches;
left: blank near the bottom where promotion text usually goes;
right: vendor sample version)



Eskimo Pie Co., "ELGIN ICE CREAM", circa 1940's?
(cardboard box and 9 wood pieces, 4 by 3.25 by 1/2 inches;
directions on inside of box top and solution sheet included;
different versions different Ice Cream distributor on the box top)

Copyright J. W. Hayward 1926,
manufactured by the Standard Trailer Company, Cambridge Springs, PA,
distributed by S-M News Co., Inc., 229 Fourth Ave., New York, NY.
(cardboard box and 9 wood pieces, 4 by 3.25 by 1/2 inches)
Here are the top / bottom (left below) and left / right (right below) box edges:




Here are the directions:


Copyright Standard Trailer Co. 1953.
(cardboard box and 9 plastic pieces, 4 by 3.25 by 1/2 inches)


"Pilgrim's Progress Puzzle", Cross Publishing, Copyright 1957.
(cardboard box and 9 plastic pieces, 3.25 by 4 by 5/16 inches)

C. O. Luce 1953, purchased by J.A. Storer as a child circa 1962.
(cardboard box and 10 plastic pieces, 4 x 3.25 x 1/2 inches)


"Stranded in Space", made in England, circa 1970's?
(cardboard card and 10 plastic pieces, puzzle is 4 x 3.25 x 1/2 inches)




Adams "Moving Day Puzzle", circa 1930.


metal tray and lid with nine metal pieces, 3.8" x 3.1" x 5/16";
along the top is shown a packaged puzzle that came with bottom nested inside the cover,
with folded solution sheet and directions summary between them;
the package back instructs one to move the piano and also has adds for other products;
on the upper right is a second one of these puzzles with a white piano square;
the solution first presents Dads Puzzler Diagonal and then the standard puzzle,
where the solutions allow one to push two or three blocks together)





Adams Company, circa 1940's.
(heavy metal tray and lid with nine metal pieces, 4" x 3.25" x 1/4",
pieces slide well with a nice fit;
directions on the box bottom, solution sheet included;
these versions the same except for case cover color;
the next page shows a newer version that is shown on page 62 of the Adams Co. History book)


Adams Company, circa 1950's.
(heavy metal tray and lid with nine plastic pieces, 3.8" x 3.1" x 5/16";
solution taped into inside of top cover;
shown on page 62 of the Adams Co. History book)

Adams Company, 1961.
(metal tray and nine plastic pieces, 3.75 x 3 x 5/16 inches;
shown on page 108 of the Adams Co. History book)
Came with solutions to both Dad's Puzzler and Dads Puzzler Diagonal:


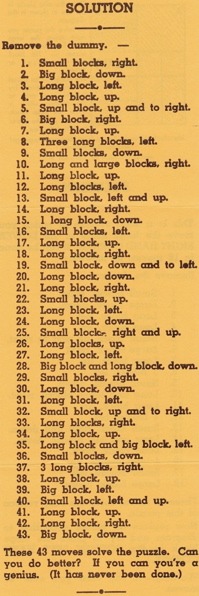



Dads Move A Block, unknown date.
(5.5 by 4 by 1.125 inch high wood box with wood pieces)

(wood box with 9 wood pieces, 4.1" x 3.32" x 5/8")



Central Specialty Co., Hutchinson, Kansas, unknown age.
(cardboard box and 9 wood pieces, 4.1" x 3.3" x 7/16""; directions inside of box top)




Leech Products Co., Hutchinson, Kansas, unknown age.
(cardboard box and 9 wood pieces, 3.5" x 2.8" x 5/16"; directions inside of box top)


Piedmont Premium Beer., undated.
(cardboard box and 9 wood pieces, 4 by 3.25 by 9/16 inches)


Frigidaire Jumble Puzzle, undated.
(cardboard box and 9 cardboard pieces, 3 by 2.5 by 5/16 inches)




Dad's Puzzle, Drueke Blue Chip Game Company, 1972.
(cardboard box and 9 wood pieces, 6" x 4+7/8" x 9/16")

Magnetic Square Puzzle,
WM. F. Drueke & Sons, Inc., Grand Rapids, MI, copyright 1961.
(plastic pieces with magnetic backs in cardboard box with metal bottom,
7.8 by 7.8 by 5/8 inches)

Kasko Puzzler, "REG US PAT OFF".
(cardboard box and 9 wood pieces, 4 by 3.25 by 1/2 inches)



Crane Packing Co., Chicago, Copyright J. W. Hayward 1926.
(cardboard box and 9 wood pieces, 4" x 3.25" x 1/2"; directions inside box top)


Nevers Crafts Shop, Ossipee, N. H., 1950's?
(cardboard box and 9 wood pieces, 5+5/16" x 4+5/16" x 1/2")




MOVING Puzzle, Copyright Frederick E. Aaron 1941,
"Hasley Bros. MOVING AND STORAGE", Pittsburgh, PA.
(cardboard box and 9 wood pieces, 4" x 3.25" x 1/2"; directions inside box top)



Moving Puzzle, Copyright Frederick E. Aaron 1927,
"GREYVAN STORAGE, INC. 1665 Main St., Buffalo 8, N.Y.".
(cardboard box and 9 wood pieces, with solution sheet, 4 by 3.25 by 1/2 inches)



Motor Grinding Co., copyright J. W. Hayward 1926.
(cardboard box and 9 wood pieces, 4 by 3.25 by 1/2 inches;
directions on inside of the box top)




F. C. Bellis Independent Oil, patent applied for, copyright J. W. Hayward 1926.
(cardboard box and 9 wood pieces, 4 by 3.25 by 1/2 inches;
2x2 piece has paper label; directions on inside of the box top)





Ohio Table Pad Co., copyright J. W. Hayward 1926.
(cardboard box and 9 wood pieces, 4 by 3.25 by 7/16 inches)
Some More Examples Of Dad's Puzzles
Walton Patent,, from: www.uspto.gov - patent no. 516,035Filed Mar. 14, 1893; granted Mar. 6, 1894.Moss Patent,, from: www.uspto.gov - patent no. 668,386
Block puzzle with 1x2 size blocks.Filed June 8, 1900; Feb. 19, 1901.Hardy Patent, from: www.uspto.gov - patent no. 1,017,752
Colored sliding blocks.Filed Dec. 14, 1907; granted Feb. 20, 1912.Kuczynski Patent, from: www.uspto.gov - patent no. 6,039,318
Shows as its preferred embodiment (Figure 1) a 4x4 tray with ten pieces
(one 2x2, three 1x2, two 2x1, and four 1x1).
Claims 8 and 9 addresses a general class of sliding block puzzles with three sizes of pieces,
and Claim 10 addresses puzzles with one 2x2 piece,
some number of 1x2 and 2x1 pieces, and some number of 1x1 pieces.Filed Mar. 4, 1998; granted Mar. 21, 2000.
Figures show Dad's Puzzler and specifications describe a frame for holding it.

Circa 1930's.
(cardboard box and 9 wood pieces, 4" x 3.25" x 1/2")
Move the 2x2 piece from the lower right to the upper right (without picking up pieces). Turn the puzzle upside-down and it is identical to the Dad's Puzzler except that the 1x1 pieces are shifted right 2 units. The inside of the cover has a 5 page pamplet glued to it:


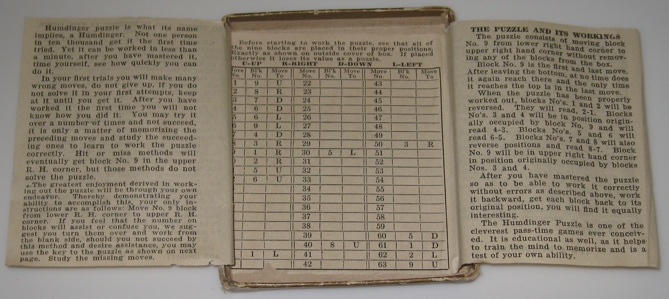
Since the first two moves of the solution presented for Dad's Puzzler are to move the two 1x1 pieces right, a Humdinger solution can be formed by skipping positions 0 and 1 of the Dad's Puzzler solution, giving 60 straight-line moves that can be converted to 57 rectilinear moves by combining steps 4/5, 25/26, and 56/57:

(one move = sliding one piece any number of units in one direction)

U Try It, circa 1930's.
(cardboard box and 9 wood pieces, 5" x 4" x 3/4")
Here is what the directions on the box say:

"Place the blocks as per the above chart and, by
sliding without removing or turning them,
you must get No. 9 to the position of 7 and 8."

Unknown age (sleeve with directions added by J. Storer 2007).
(cardboard sleeve, stained pine tray, 9 walnut pieces, 5.5" x 4.75" x 1.25",
the 2x2 piece is made by gluing two 1x2 pieces together,
the 2x2 has a metal tack on each side and the other have on in the middle,
pencil markings on the tray show a Humdinger start position,
sleeve also has directions for Nine Block, Quzzle, and Quzzle Killer)


New Deal, circa 1930's.
(cardboard box and 9 wood pieces, 3.4" x 4.1" x 1/2")
Further Reading
New Deal Wikipedia Page, from: http://en.wikipedia.org/wiki/New_Deal





"Infants' Hospital Puzzle", Chad Valley Co. Ltd., Harborne, England, 1920;
made for the Infants Hospital in Vincent Square, London, founded by R. Mond.
(cardboard box and 9 cardboard pieces, 6.2 by 5.2 by 1/2 inches;
see also Infants' Hospital Puzzle, Infants' Hospital - The Magic Line, A Ward Oin The Infants' Hospital, Infants' Hospital Jigsaw Puzzle)
This is an example of a version of "Dad's Puzzler". where the directions give additional constraints on the final position; see the following pages.
Further Reading
Infants Hospital History, from: http://ezitis.myzen.co.uk/westminsterchildrens.html
Robert Mond Wikipedia Page, from: http://en.wikipedia.org/wiki/Robert_Mond
The directions to the puzzle on the preceding page say one must not merely move the 2x2 piece to the lower left as with the standard Dad's Puzzler, but it must be exchanged with the two pieces there. Here are a number of interpretations of what this means:
The minimal length solution for the standard version (62 straight-line moves, 59 rectilinear moves) also works for the excange version. When the exchange must be strict, here is a 67 straight line moves solution; it can be converted to 65 rectilinear moves by combining steps 6/7 and 63/64:
Here is a 64 straight line moves solution; it can be converted to 61 rectilinear moves by combining steps 6/7, 27/28, 58/59:
Here is a 69 straight line moves solution; it can be converted to 67 rectilinear moves by combining steps 6/7, 63/64:
Here is a 167 straight line moves solution; it can be converted to 165 rectilinear moves by combining steps 6/7, 161/162:

(continued on the next page)
Here is a 167 straight line moves solution; it can be converted to 165 rectilinear moves by combining steps 6/7, 161/162:


Quzzle designed by Jim Lewis circa 2000.
(cardboard box containing plastic tray and 9 plastic pieces, 5.9 x 4.9 x 1/2 inches)
Uses 1x1, 1x2, 2x1, and 2x2 pieces on a 4x5 board like Dad's Puzzle. Below, from the start position shown on the left, slide pieces (without picking them up) to form the end position (a mirror copy of the start position) shown on the right:
It turns out that if the goal is stated to simply to be, from the start position, move the 2x2 to the upper right corner (so it doesn't matter what happens to the other pieces), then a minimal length solution of 93 straight-line moves (equivalent to 84 rectilinear moves) makes a mirror image, and so this simpler problem has the same basic complexity. When it was introduced, Quzzle was known for requiring a large number of moves for puzzle of its type. There are puzzles in Dad's Puzzle family that require many more moves (e.g., Century Puzzles), and even with exactly the same set of pieces as Quzzle, there are puzzles that require more moves. For example, Quzzle Killer of B. Henderson and Gil Dogon (discussed on Pegg's Page and you can play on Baxter's Page) requires more moves just to get the 2x2 piece to the upper right, and 6 additional moves to make the mirror image:
Further Reading
Quirkle Page, from: http://www.quirkle.com
Quzzle Page, from: http://www.quirkle.com/puzzle/index.htm
Quzzle Tips Page, from: http://www.quirkle.com/puzzle/tips.htm
Pegg's Page, from: http://www.maa.org/editorial/mathgames/mathgames_12_13_04.html
Baxter's Page, from: http://www.puzzleworld.org/SlidingBlockPuzzles/qkiller.htm
Here is the solution from the Quzzle Tips Page uses 95 straight-line moves.

Here is a solution of 93 straight-line moves; it corresponds to 84 rectilinear moves (by combining steps 5/6, 14/15, 20/21, 25/26, 34/35, 37/38, 73/74, 79/80, 88/89).

Here is a (minimal) solution of 99 straight-line moves that solve basic Quzzle Killer followed by an additional 6 moves (105 total) to solve the full mirrored version; it cn be converted to 90 rectilinear moves (also known to be minimal) by compining steps 11/12, 20/21, 26/27, 31/32, 40/41, 43/44, 79/80, 85/86, 94/95 for basic Quzzle Killer followed by 6 more moves:


Originally manufactured by Kum-Bak Sports, Toys & Games London, circa 1935;
this puzzle a 1961 Adams Co. Dad's Puzzle,
with cardboard sleeve by J. A. Storer 2007.
(cardboard sleeve, metal tray, and 9 plastic pieces, 3.75 x 3 x 5/16 inches,
the sleeve has directions for Nine Block, Dad's Puzzler, Quzzle, and Quzzle Killer)
The same piece set as Dad's Puzzler, and infact, this name is sometimes used to refer to Dad's Puzzler (e.g., in the Filipiak book). It is presented on the web page of Hirofumi Fujiwara as puzzle 17 of his "Step By Step Problems", and also in the Hordern book.
The start position is different from Dad's Puzzler, but the problem is the same; slide the 2x2 piece from the upper left to the lower left (without picking up pieces):
Here is a solution of 47 straight-line steps; it can be converted to 45 rectilinear moves by combining steps 6/7, 36/37:
(one move = sliding one piece any number of units in one direction)
Like Dad's Puzzler Diagonal, it is natural to consider moving the 2x2 piece to the lower right corner than the lower left:
Like Dad's Puzzler, the diagonal version of Nine Block is an easier problem. Here is a solution of only 29 straight-line moves that can be converted to 27 rectilinear moves by combining steps 6/7 and 18/19:

a.k.a. L'Ane Rouge, Which Way Out, Psychotease,
Escaping Jail, Cao Cao Escape, Klotski
Patented in England by J. H. Fleming 1932,
this one is "Which Way Out" by T.C. Timber Brain Twisters circa 1995,
in a box made by J. A. Storer 2007.
(maple, tray and 10 pieces, 2x2 is painted red, 3.75 x 3.5 x 0.9 inches;
box is resized cigar box with brass hardware, 4.75 x 4.75 x 1.75 inches,
lid diagram also shows Simple Traffic Jam, Century, and Super Century)
Hordern's book credits the Red Donkey as the third most sold sliding block puzzle (after the Fifteen puzzle and Dad's Puzzler). It is shown in the 1996 design patent of Mendelsohn and the 200 patent of L. Aryan. The goal is to slide the 2x2 piece (without picking pieces up) to the bottom center so that it can pass out through the opening (we do not charge an extra move for the the 2x2 piece passing through the opening). This puzzle is like Simple Traffic Jam, with the 1x2 piece between the 2x2 and 1x1's. There are a number of starting position variations, the leftmost being the original French L'Ane Rouge:



The September 2000 patent of L. A. Aryan describes the same puzzle as the Red Donkey puzzle. Figure 1 shows the puzzle (the box lid is corrected in a revised Figure 1 at the end of the patent). The claims describe a ten piece sliding piece puzzle with a hinged lid. Some study might be required to determine exactly what is new about this patent. Figure 4 presents a (not minimal) solution of 22 positions that require multiple moves (a total of 99 straight-line moves):
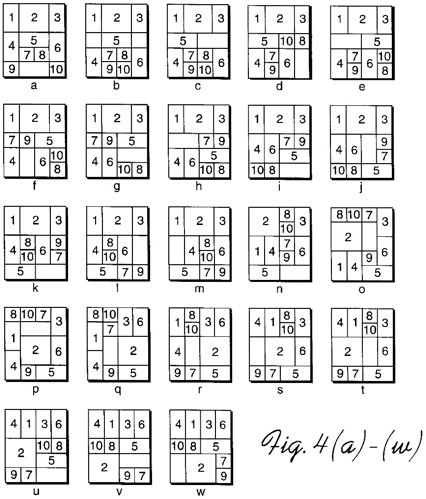
Here is the solution idea that came with Which Way Out. Many of these positions represent several moves (a total of 118 moves straight-line moves):


Here is a solution of 90 straight-line moves for Version A; it can be converted to 81 rectilinear moves by combining steps 10/11, 14/15, 24/25, 39/40, 47/48, 52/53, 55/56, 79/80, and 88/89:

The solution presented on the preceding page for Version A (and also the 81 rectilinear moves solution that is presented in Hordern's book - Puzzle C27d) is minimal and reaches exactly the same position at Step 4 as does a minimal 81 rectilinear moves solution (90 straight-line moves) for the Version B and C start positions (and so step 4 onward can be used for all three puzzles):
The Winning Ways book shows the Version D start position. Step 6 of a minimal solution for this variation is exactly the same as Step 4 above, and so this variation has a minimal solution (for both straight-line and rectilinear moves) of 2 moves longer than Versions A, B, and C (pieces 1, 2, 3, 4 must be renamed to 3, 1, 2, 4):

Simple Traffic Jam
Shafir Games 1981;
minimal solution of 64 rectilinear moves.
Century
Designed by J. H. Conway 1975;
minimal solution of 99 rectilinear moves.

Super Century
Designed by Gil Dogon 2004;
minimal solution of 138 rectilinear moves.


Psychotease, copyright 1969.
(cardboard box and 10 wood pieces, 9 x 11 x 1.5 inches)


Escaping Jail, copyright University Games Co. 1993, made by Raintree Puzzles.
(wood box and 10 wood pieces, 4.4 x 3.25 x 1.2 inches)


Cao Cao Escape, LEO Marketing, 1995
(wood box and 10 wood pieces, 3.8 x 3.125 x 3/4 inches)
Further Reading
Wikipedia Klotski Page, from: http://en.wikipedia.org/wiki/Klotski
Pegg's Page, from: http://www.maa.org/editorial/mathgames/mathgames_12_13_04.html
Baxter's Page,, from: http://www.puzzleworld.org/SlidingBlockPuzzles/4x5.htm
Aryan Patent, from: www.uspto.gov - patent no. 6,116,600
Armendariz Design Patent, from: www.uspto.gov - patent no. 367,502
Mendelsohn Design Patent, from: www.uspto.gov - patent no. 388,840


Shafir Games 1981.
(cardboard cover, plastic tray, and 10 plastic pieces, 4.8 by 4 by 3/8 inches)
Uses 1x1, 1x2, 2x1, and 2x2 pieces on a 4x5 board in the theme of Dad's Puzzler and Red Donkey. This puzzle is described in Hordern's book (puzzle C28); it is also shown in Figure 1 of a 1990 patent of T. Monoyios. From the start position shown on the left, slide pieces (without picking them up) to form the end position shown on the right:Here are the directions from the back of the box: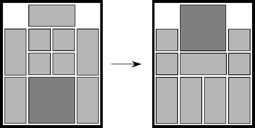


The basic steps for one approach to solve Traffic Jam are shown below, although there are many shorter solutions (the following page shows a minimal length solution).
Here is a solution of 69 straight-line moves; it can be converted to 61 rectilinear moves by combining steps 4/5/6 to 2 moves (rename 243 to 324) and combining steps 2/3, 12/13, 20/21, 26/27, 29/30, 53/54, and 62/63 (89 unit moves are used, although 87 unit moves are possible):

(one move = slide one piece any number of units in one direction)
It is natural to consider the simpler puzzle where we only care about the 2x2:
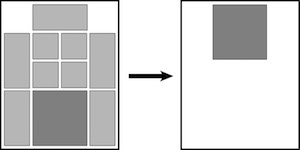
Simple Traffic Jam
Fewer moves are required if starting from the final position of Traffic Jam::
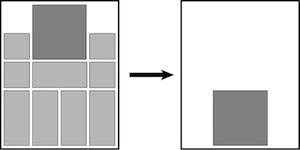
Reverse Simple Traffic Jam
Here is a 39 straight-line moves solution; it can be converted to to 34 rectilinear moves by combining steps 7/8, 16/17, 25/26, 28/29, 30/31:
(one move = slide one piece any number of units in one direction)
Further Reading
Monoyios Patent, from: www.uspto.gov - patent no. 4,927,150
Ling Design Patent, from: www.uspto.gov - patent no. 450,356

Century by J. H. Conway 1975, Super Century by Gil Dogon 2004;
this puzzle formed from two 1961 Adams Co. Dad's Puzzles,
with cardboard sleeve by J. A. Storer 2007.
(cardboard sleeve, metal tray, and 10 plastic pieces, 3.75 x 3 x 5/16 inches)
The Century puzzle is to move the 2x2 piece to the bottom center without regard to where the remaining pieces go. Century is discussed in the Winning Ways book vol. 2 and shown on a chart on Baxter's Page. Its name reflects a minimal solution of exactly 100 rectilinear moves formed by an initial 1/2 unit move of the central 2x1 piece followed by exactly 99 moves that end with a move of a 2x1 piece back to the middle. It is natural to consider a puzzle where the last position is fully specified; Century and a Half (also discussed in Winning Ways vol. 2) makes a vertical mirror of the start position, where its name reflects its solution of exactly 150 rectilinear moves formed by an initial 1/2 unit move of the central 2x1 piece followed by exactly 149 moves that end with a move of a 2x1 piece back to the middle.
Century
Century and a Half
The Super Century puzzle, using the same set of pieces as Century, is also to move the 2x2 piece to the bottom center without regard to where the remaining pieces go. Super Century is discussed in an article by E. Pegg and shown on a chart on Baxter's Page. It has a minimal solution of 138 rectilinear moves. Again, it is natural to consider a puzzle where the last position is fully specified. We refer to New Century as making a vertical + horizontal mirror of the start position; it has a minimal solution of 230 rectilinear moves.
Super Century
New Century
Here are every 3 steps of a 99 rectilinear steps solution (which can be converted to 111 straight-line steps by replacing with two steps each of steps 1, 4, 15, 18, 22, 25, 46, 48, 51, 77, 78, 98). This represents exactly 100 rectilinear steps when the initial 1/2 unit move is included.
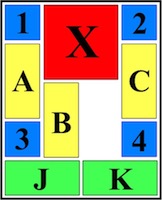
Here are every 5 steps of a 149 rectilinear steps solution (which can be converted to 170 straight-line steps by replacing with two steps each of steps 1, 4, 15, 18, 20, 23, 30, 37, 41, 49, 71, 72, 98, 101, 103, 123, 127, 131, 134, 145, 148). This represents exactly 150 rectilinear steps when the initial 1/2 unit move is included.
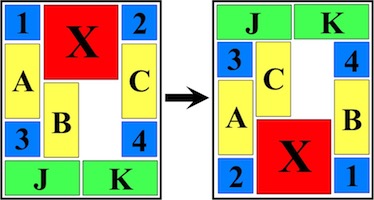
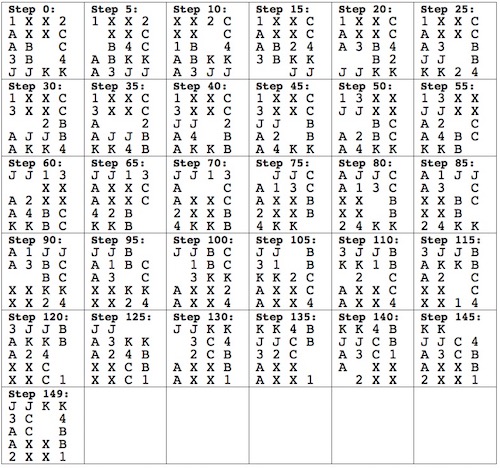
Here are every 4 steps of a 138 rectilinear steps solution (which can be converted to 150 straight-line steps by replacing with two steps each of steps 26, 28, 51, 53, 56, 65, 85, 87, 90, 116, 117, 137).
Here are every 7 steps of a 230 rectilinear steps solution (which can be converted to 254 straight-line steps by replacing with two steps each of steps 28, 51, 53, 56, 70, 75, 79, 83, 86, 88, 91, 111, 114, 115, 141, 144, 146, 166, 175, 178, 180, 203, 205).
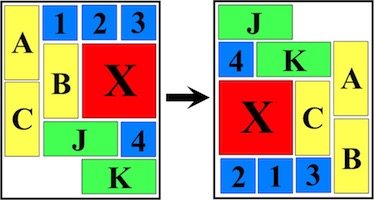
New Century does not end with the 2x2 piece centered at the bottom (since it produces a vertical + horizontal mirror of a start position that does not have the 2x2 piece centered at the top). However, it is natural to consider a "nice" fully specified ending position that does. One idea is ending with the two 1x2 pieces replacing the 2x2 piece:
Super Century 198
Here are every 10 steps of 198 rectilinear steps for Super Century 198 (which can be converted to 217 straight-line steps by replacing with two steps each of steps 26, 28, 51, 53, 56, 65, 85, 87, 90, 110, 113, 114, 140, 143, 145, 165, 173, 178, 189):
Further Reading
Pegg's Page, from: http://www.maa.org/editorial/mathgames/mathgames_12_13_04.html
Baxter's Page, from: http://www.puzzleworld.org/SlidingBlockPuzzles/4x5.htm


Made in Asia, purchased 2007.
(felt lined wood tray and 10 wood pieces, 8 by 8.5 by 1 inches)
The directions show Red Donkey (Version C) and some other problems including Little House.


Here is every 8th move of a solution to Little House of 250 straight-line moves, which can be converted to 233 rectilinear moves by combining 7/8, 41/42, 64/65, 75/76, 87/88, 91/92, 94/95, 118/119, 128/129, 134/135, 138/139, 165/166, 189/190, 192/193, 196/197, 208/209, 220/221. Positions 18 and 21 are also shown; by replacing moves 19 to 21 by two rectilinear moves, a solution results that is minimal for the straight-line and unit metrics, and only one move longer than a minimal 231 rectilinear moves solution (see the following page):
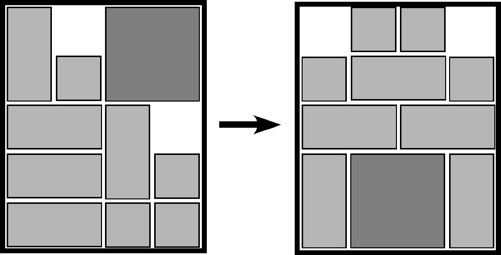
Little House
(Pierre-Francois Culand)
(one move = slide one piece any number of units in one direction)
Here is every 7th move of a solution of 231 rectilinear moves solution:
(one move = slide one piece any number of units in any number of directions)

Originally made by Himawari Japan 1981;
this puzzle formed from two 1961 Adams Co. Dad's Puzzles,
with cardboard sleeve by J. A. Storer 2007.
(cardboard sleeve, metal tray, and 10 plastic pieces, 3.75 x 3 x 5/16 inches,
the sleeve has directions for Ushi and Ushi Flipped))
The standard Ushi puzzle is shown on the left and on the right is a common variation where the center portion is flipped:

Ushi
Ushi Flipped
Here is a Ushi solution of 108 straight-line moves; it can be converted to 98 rectilinear moves by combining steps 11/12, 16/17, 20/21, 27/28, 38/39, 50/51, 54/55, 57/58, 81/82, 106/107:

Here is a Ushi Flipped solution of 110 straight-line moves; it can be converted to 103 rectilinear moves by combining steps 28/29, 40/41, 52/53, 56/57, 59/60, 83/84, 108/109:



Copyright University Games Co. 1997, made by Sports Pack Puzzles.
(wood box and 11 wood pieces, 4.4 x 3.25 x 1.2 inches)
Here is a solution of 61 straight-line moves; it can be converted to 48 rectilinear moves by combining steps 4/5, 7/8, 14/15, 19/20, 21/22, 25/26, 29/30, 32/33, 36/37, 39/40, 46/47, 50/51, and 59/60:

The Royal Out puzzle is described in Hordern's book as a collection of 5 puzzles consisting of Red Donkey (Version A) and 4 others; of those four, the one shown here requires the greatest number of moves. The King Out puzzle is Hole In One with the bottom row shifted up two units.
Hole In One

Royal Out

King Out

The first 2 straight-line moves of a minimal solution to Royal Out, which can be converted to 1 rectilinear move, yield the start position for Hole In One. Hence, Royal Out Can be solved with 63 straight-line moves, which can be converted to 49 rectilinear moves (by combining steps 1/2 of Royal Out and making the 13 combinations for Hole In One).

Royal Out Minimal Solution First Three Moves
The first 5 straight-line moves of a minimal solution to King Out, which can be converted to 4 rectilinear moves, yield position 15 of Hole In One (the 1x1 pieces can be renamed). Hence King Out can be solved with 51 straight-line moves, which can be converted to 40 rectilinear moves by combining steps 4/5 of King out and steps 19/20, 21/22, 25/26, 29/30, 32/33, 36/37, 39/40, 46/47, 50/51, and 59/60 of Hole In One.

King Out Minimal Solution First Five Moves


Originally manufactured by Hanabishi 1984;
left purchased in Japan 2010, right made by J. A. Storer 2007.
(left: cardboard box, 11 wood pieces + keeper, 4.75" x 5.8" x 7/16";
right: box, 11 purple heart and cherry pieces + keeper, 5" x 6.1" x 1.25")
The object is to move the cow inside the fences:
Here is the solution that was sold with the puzzle:
Here is a solution of 82 straight-line moves; it can be converted to 71 rectilinear moves by combining steps 2/3, 15/16, 19/20, 23/24, 26/27, 30/31, 33/34, 40/41, 45/46, 58/59, and 62/63 (this solution remains minimal even if graphics are ignored, and no solution is possible if the lower right two square are required to be blank):

(one move = sliding one piece any number of units in one direction)

Made by J. A. Storer, 2007.
(wood box with plexiglass bottom, lid, and 13 pieces, 5.75" x 7.75" x 1.25")
A box with a 4x5 tray and a 4x1 side tray to hold unused pieces. There are a total of six 1x1 pieces, six 1x2 pieces, and one 2x2 piece. Many classic 4x5 tray puzzles can be played; Dad's Puzzler, Nine Block, Quzzle / Quzzle Killer, Traffic Jam, Red Donkey, Century, Super Century, Century And A Half, Little House, Ushi, Hole in One, King Out, etc. Hordern's book shows many other puzzles that can be played. Another source for 4x5 tray puzzles is Fujiwara's Step by Step Problems page, which gives 25 problems of increasing difficulty (along with solutions if you get tired). Here are three of them and also Super Compo (designed by Junk Kato - see Baxter's Page), which is similar to but requires more moves that Fujiwara 25:
Fugiwara 15
Fugiwara 22
Fugiwara 25
Super Compo
Further Reading
Fujiwara's Page, from: http://www.pro.or.jp/~fuji/java/puzzle/slide/V1.0/fuji.index-eng.html
Baxter's Page, from: http://www.johnrausch.com/SlidingBlockPuzzles/4x5.htm
Here is a solution of 47 straight-line moves; it can be converted to 43 rectilinear moves by combining steps 13/14, 27/28, 33/34, 45/46:
(one move = sliding one piece any number of units in one direction)
Here is a solution of 64 straight-line moves; it can be converted to 62 rectilinear moves by combining steps 11/12, 53/54:

(one move = sliding one piece any number of units in one direction)
Here is a solution of 111 straight-line moves; it can be converted to 101 rectilinear moves by combining steps 2/3, 19/20, 23/24, 30/31, 41/42, 53/54, 57/58, 60/61, 84/85, 109/110:

(one move = sliding one piece any number of units in one direction)
Here is a solution of 132 straight-line moves; it can be converted to 123 rectilinear moves by combining steps 32/33, 39/40, 42/43, 62/63, 74/75, 78/79, 81/82, 105/106, 130/131:

(one move = sliding one piece any number of units in one direction)

Designed by Dries De Clercq, this one assembled by J. A. Storer 2013.
(cardboard sleeve, metal tray, and 10 plastic pieces, 3.8 x 3.1 x 5/16 inches)
Here is the start position and every position in which the 2x2 piece moves, along with steps 38, 50, 135, 154, and 164 (added to fill in longer gaps) of a solution of 209 rectilinear moves (using 241 straight-lines moves, although 238 straight-line moves are possible):

Designed by Dries De Clercq, this one assembled by J. A. Storer 2013.
(cardboard sleeve with SS Dries on back, metal tray, and 10 plastic pieces, 3.8" x 3.1" x 5/16")
Here is "Super Dries", and three other variations:
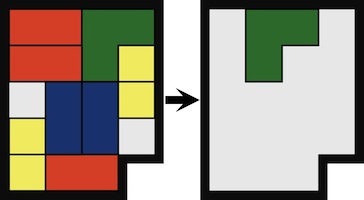
Super Dries (321 rectilinear moves)
Super Super Dries (381 rectilinear moves)
Super Super Dries 2 (396 rectilinear moves)
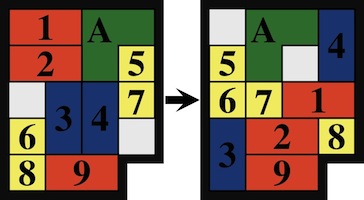
Super Super Dries 3 (403 rectilinear moves)
For Super Dries, here is the start position and every position in which the angle piece moves:


Copyright 1986 DU GLO Inc.
(plastic, pieces interlock and don't fall out when puzzle is turned over, 4.7" x 3.25" x 1/2")
Directions are on the back. Here is every 10th position and each position that the 2x2 piece moves in a 95 rectilinear moves (98 straight-line moves, 124 unit moves) solution; note that at move 80, with no change to the number of straight-line or unit moves, an extra rectilinear move (for 96 rectilinear moves total) keeps pieces A and B in the same left to right order at the end:



a.k.a. Infants Progress Puzzle
Chad Valley Co. Ltd., Harborne, England, 1920;
made for the Infants Hospital in Vincent Square, London, founded by R. Mond.
(cardboard box, 1/4" thick cardboard tray with 10 pieces, 6.75" x 5+7/8" x 9/16";
instructions on the underside of the box top;
Hordern's book gives the date and a 28 rectilinear /35 straight-line moves solution;
see also Dad's Puzzler - Exchange Version / Infants Hospital, Infants' Hospital - The Magic Line, A Ward Oin The Infants' Hospital, Infants' Hospital Jigsaw Puzzle)
Here is a 26 rectilinear moves (32 straight-line moves) solution:


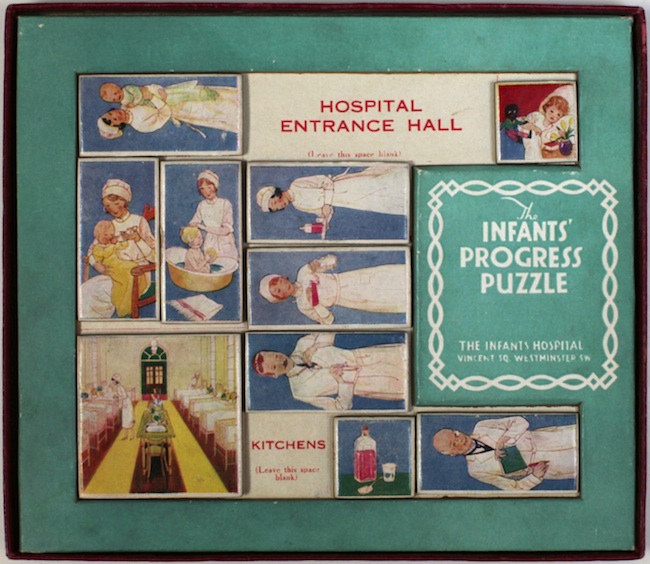
Further Reading
Infants Hospital History, from: http://ezitis.myzen.co.uk/westminsterchildrens.html
Robert Mond Wikipedia Page, from: http://en.wikipedia.org/wiki/Robert_Mond


a.k.a. Ten Block Puzzle, Traffic Cop Tangle
George E. Schweig and Son, Philadelphia PA.
(cardboard box and ten wood pieces, 4 x 3.25 x 1/2 inches)
Exchange the two 2x2 pieces. Described on pages 12-13 of the 1942 Filipiak book (which gives a 55 rectilinear moves / 70 straight-line moves solution). Below are all of the steps that move a 2x2 piece in a solution of 47 rectilinear moves (55 straight-line moves) that is presented in Hordern's book (pieces numbered the same with M,W instead of A,B):
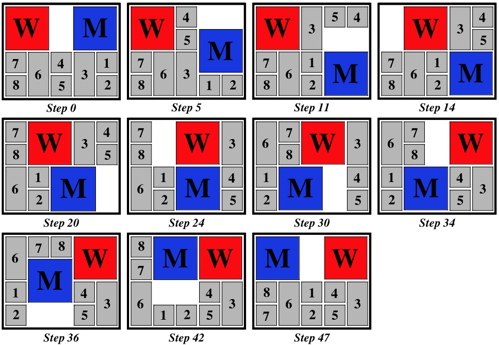
This solution is on the inside of the green cover shown on the preceding page.


Made in Japan by Hanabishi, circa 1985.
(cardboard box, wood tray, 2 keepers and 16 wood pieces, 4.75 x 9 x 5/8 inches)
A 4x3 portion on the left and a 4x5 portion on the right with a 2 unit high opening between; remove keepers and slide the pieces to make the 2x2 pieces meet. The right side is the Ushi puzzle, but solving is easier by making use of extra space on the left. Here are every 4th position of a 32 rectilinear (46 straight-line) moves solution that ends with the couple meeting along a unit long portion of their edges:
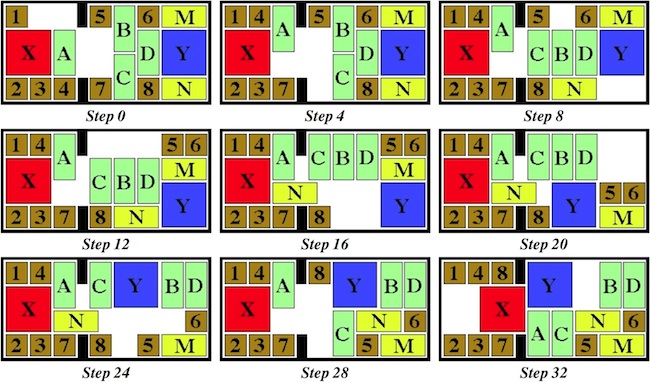
To meet on a full edge, here are 10 positions of a 39 rectilinear (64 straight-line) moves solution:
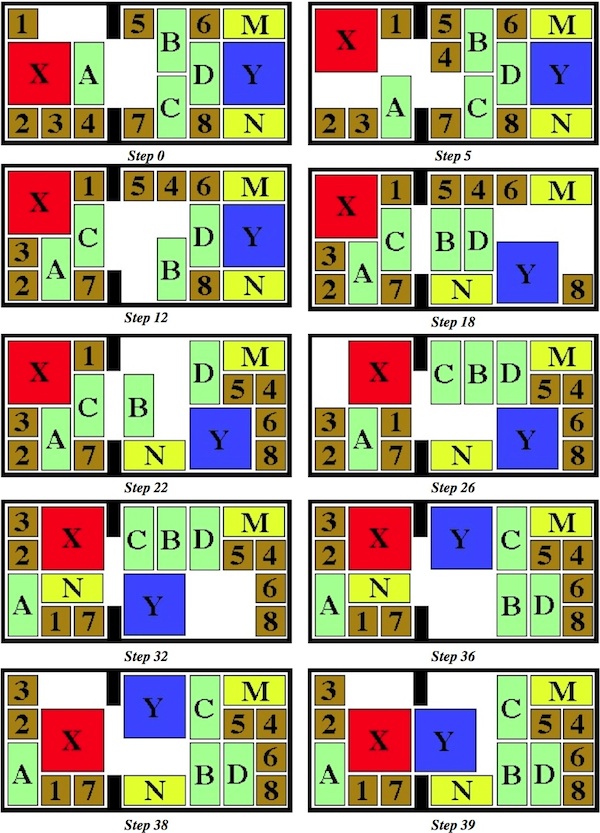
To meet on a full edge, here are 10 positions of a 39 rectilinear (59 straight-line) moves solution:
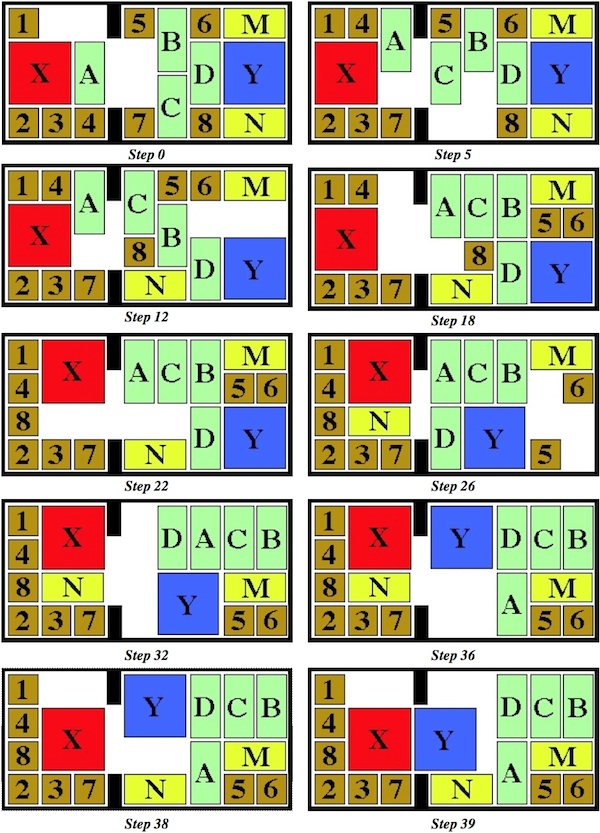
With the supply of extra pieces on the left, any of the Dad's Family puzzles can be played on the right (Dad's Puzzler, Traffic Jam, Red Donkey, Century, Hole In One, Ushi, etc.). Puzzles with two 2x2 pieces and puzzles played in a 4 by 3 area are also possible.
Ten Block: Presented in the 1942 Filipiak book (a.k.a. Trans-Atlantic Puzzle, Traffic Cop Tangle), the problem is to exchange the two 2x2 pieces; below are all of the steps that move a 2x2 piece in a solution of 47 rectilinear moves (55 straight-line moves) that is presented in Hordern's book (pieces are numbered the same as in that solution with M,W instead of A, B):
Hughes Puzzle: The Hordern book Hordern book, describes the Hughes Puzzle as having been submitted to Amateur Handicraft Magazine USA by F. Clark Hughes in 1947. The problem is to move the 2x1 piece from the upper left to the lower right; here are every 6 steps of a solution of 23 rectilinear moves (27 straight-line moves) that is presented by Hordern:
Boxes with an aspect ratio of about two to one are relatively common. The thickness of an inside liner and the thickness of the left to right dividers can be adjusted to make the 4:3 and 4:5 aspect ratios of the left and right sides exact.

Made by J. A. Storer, 2007.
(wood box, 2 plexiglass keepers, and 16 wood pieces, 5.1 by 9.6 by 1.25 inches;
box originally for an old Starrett Micrometer; underside of lid has directions drawn)


Made by J. A. Storer, 2007.
(wood box, 2 plexiglass keepers, and 16 wood pieces, 3.9 by 7.75 by 1.1 inches;
box originally for some Yema Tostada - a Spanish dessert)
Here are the directions from the back of the box and the solution sheet. It shows the couple meeting along a full edge, with the meeting edge to the left of the center bar. The 32-move solution for them to meet on a 1-unit portion needs to have the meeting edge to the right of the bar (otherwise it takes 35 moves), whereas the 39 move solution works either way (depending on the choice for steps 38 and 39).
Further Reading - Baxter's Sliding Block Pages, from:
(Main), from: http://www.johnrausch.com/SlidingBlockPuzzles
(Happy Couple), from: http://www.puzzleworld.org/SlidingBlockPuzzles/happyCouple.htm
(Ten Block), from: http://www.johnrausch.com/SlidingBlockPuzzles/10block.htm
(Hughes), from: http://www.johnrausch.com/SlidingBlockPuzzles/hughes.htm



a.k.a. Starry Puzzler, Tit-Bits Teaser No. 2, Ching Foo,
South Pole Expedition, Straight Arrow Puzzle
Patented by J. M Schneider 1928.
(cardboard box and 14 wood pieces, 4 by 4.75 by 1/2 inches,
box cover at the bottom says "PATENT NO 1663568. MARCH 27, 1928";
inside of the box cover has the solution shown above)
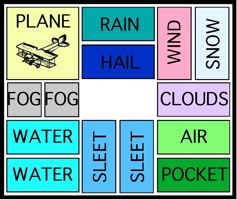
Hordern's book presents a solution of 55 rectilinear moves (59 straight-line moves); here are each of the positions after the plane moves, and two others of the first 25 (labels have been added to match Hordern's):
Hordern's book also presents a solution of 129 rectilinear moves (133 straight-line moves) for the harder problem of ending in a position which is the same as the start upside down. The first 28 moves are the same (shown in more detail in the first row above); here are each of the positions after the plane moves, and three others:


The Starry Puzzler, John M. Schneider Detroit Michigan, 1926.
(cardboard box and 14 wood pieces, 4 by 4.75 by 1/2 inches)
This 1926 version says it is manufactured by the inventor of the 1928 patent on this puzzle (filed March 1927). Written inside of the box top is: "This puzzle is easy to do if you know how, and I am the guy that knows how. $50 reward for any one that puts it together or a new dress."



Tit-Bits Teaser No. 2, George Newnes, London, Made in the U.S.A., circa 1928.
(cardboard box and 9 wood pieces, 4 by 4.75 by 1/2 inches; date is not shown, but is listed in Hordern's book as 1928)



Ching-Foo, Southwestern Distributing Co., Hutchinson, Kansas, 1927.
(cardboard box and 14 wood pieces, 4 by 4.75 by 1/2 inches;
the problem description is a symmetric version of the Flying Puzzle;
the white box has stamped on the back "The Rexall Store ST. MARYS, KANS.")


Ching-Foo, Premier Novelty Co., Denver, Colorado, undated.
(cardboard box and 14 wood pieces, 4 by 4.75 by 1/2 inches;
slightly different cover art than the ones on the previous page)
The version of the Flying Puzzle shown first on the left below has an undated patent reference on the box top (shown on the right below) and the solution is on a piece of paper rather than on the inside of the box top (shown below); the second version shown on the left below has no copyright information at all (and no solution on the inside of the box top).








Bona Fide Broom Co. Pacomia CA, not dated.
(cardboard box and 14 wood pieces, 4 by 4.75 by 1/2 inches,
inside of the box top advertises Dad's and Ma's puzzles)

Standard Trailer Co. Cambridge Springs PA, not dated.
(cardboard box and 14 wood pieces, 4 by 4.75 by 1/2 inches; the inside of the box top invites you to send ten cents for a solution)

Franco-American Novelty Co., not dated.
(cardboard box and 14 wood pieces, 4 by 4.75 by 1/2 inches;
nothing is written on the inside of the box top)

Silver Label Beer, not dated.
(cardboard box and 14 wood pieces, 4 by 4.75 by 1/2 inches;
nothing is written on the inside of the box top)
Further Reading
Schneider Patent, from: www.uspto.gov - patent no. 1,663,568
Murphey Design Patent, from: www.uspto.gov - patent no. Des372,745


Randles Novelty Company, Hutchinson, Kansas, copyright 1933.
(cardboard box and 1/8 inch thick cardboard pieces 4.1 by 4.9 by 1/2 inches,
copyright shown on box top, directions on inside of box top show two puzzles;
the first puzzle is a mirror image of the Flying Puzzle;
the second puzzle is the same as Nine Block Diagonal)


Manufactured circa 1930.
(cardboard box and 15 wood pieces, 4 by 4.75 by 1/2 inches)
Move the 2x2 to each corner of the puzzle in a clockwise direction starting with the top right. Described on pages 9-12 of the 1942 Filipiak book (which gives a 465 move solution) and on page 99 of Hordern's book (which presents a 122 moves solution). Can be done in 101 moves.
Here the start position and each position after the 2x2 piece moves:

Here the start position, each position after the 2x2 piece moves, and also position 9 (to fill in the relatively large gap between position 0 and position 19). This solution has the 2x2 piece moving through but not terminating a move at the first three corners; to count visiting a corner as a separate move, a position can be added before each of positions 37, 59, and 81, for a solution of 104 rectilinear (117 straight-line) moves.


Circa 1932.
(cardboard box and 13 wood pieces, 4" x 4.75" x 7/16"; directions inside the cover)
Further Reading
Wikipedia Rosevelt Page, from: http://en.wikipedia.org/wiki/Franklin_D._Roosevelt
Wikipedia Hoover Page, from: http://en.wikipedia.org/wiki/Herbert_Hoover
Here is every 3rd step of a 37 rectilinear moves (40 straight-line moves, 54 unit moves) solution:Hoover Solution
Here is every 3rd step of a 42 rectilinear moves (44 straight-line moves, 56 unit moves) solution:


Manufactured circa 1930.
(cardboard box and 13 wood pieces, 4 by 4.75 by 3/8 inches;
move the 2x2 Royal Scott from the upper left corner to the lower right corner;
1931 solution announced on inside of the box top)
Here are Hordern's book moves 0, 11, 15, 22, 32, 45, 55, 59 for every move of the 2x2 piece:
Here are moves 0, 1, 5, 12, 22, 31, 47, 53 for every rectilinear move of the 2x2 piece:
Here are every second position of a solution of 53 rectilinear (55 straight-line) moves:



a.k.a. South Pole Expedition
Standard Trailer Co., for the World's Fair 1933.
(cardboard box and 13 wood pieces, 4"x4.75"x1/2"; directions inside the box top)
Hordern's book presents 37 moves (40 rectilinear moves) to slide EAST to the lower left and 42 moves (44 rectilinear moves) to slide WEST to the lower left; for both solutions, here are the starting position, each of the positions in after a 2x2 piece moves, and one other position:
Further Reading
Wikipedia Page, from: http://en.wikipedia.org/wiki/Century_of_progress




Standard Trailer Co., 1934.
(cardboard box and 13 wood pieces, 4" x 4.75" x 1/2";
Hordern's Book lists a puzzle of this name as the Flying Puzzle, but this one is is not.)


a.k.a. Fifteen Block Puzzle, 1-2-3 Puzzle, ABC Puzzle,
Tenderfoot's Caution, Countdown
S. S. Adams Co., Asbury Park, NJ., "PAT. APP'D FOR 1927".
(6.4 inches square by 5/8 inches thick cardboard box with 15 3/8 thick wood pieces; directions are on the inside of the box top shown on the right above; most of the right side of the box top edge is missing)
Start with the position shown above and slide the blocks to end with 1 and 3 exchanged and block 2 in its original position. Described on pages 14-15 of the Filipiak book (where a 262 move solution is presented). Hordern's book presents a 136 rectilinear move solution (135 straight-line moves) and a 148 rectilinear move solution (147 straight line moves) to the harder problem of a final position where 1 and 3 are exchanged and all other pieces are in their original positions (Hordern lists the number of straight-line moves as 1 and 2 more respectively becasue he starts with the leftmost yellow block one unit down). Both of Hordern's solutions begin with the same 72 rectilinear moves; the following three pages show these common moves and then the remaining moves for each solution.
For both of Hordern's solutions, here are moves 0, 2, 9, 12, 19, 21, 27, 30, 37, 44, 47, 50, 53, 55, 62, 65, 72; these are all of the moves of the 2x2 pieces plus move 37:
For the remainder of Hordern's first solution, here are moves 72, 79, 86, 93, 100, 104, 107, 110, 113, 115, 120, 123, 130 for the 2x2 pieces:
For the remainder of Hordern's second solution, here are moves 72, 74, 77, 80, 83, 90, 93, 102, 105, 111, 114, 117, 120, 129, 132, 139, 140 for the 2x2 pieces:


Rochester Puzzle Co., Rochester NY, circa 1930's?
(cardboard box 5" x 5" x 1/2" and 14 wood pieces;
directions on inside of box top, start position on inside box bottom)
This puzzle has almost the same starting configuration as the 1932 Model Garage puzzle (a.k.a. Spotcheck, Blocade) shown on page 103 of the Hordern book, except that the middle top two rectangles of Model Garage are oriented horizontally.
Here are the start, every tenth position, and the end position of an 83 rectilinear move solution (88 straight-line moves); pieces are labeled the same as Hordern's book uses for the Model Garage puzzle, except pieces 11 and 12 are labeled X and Y:
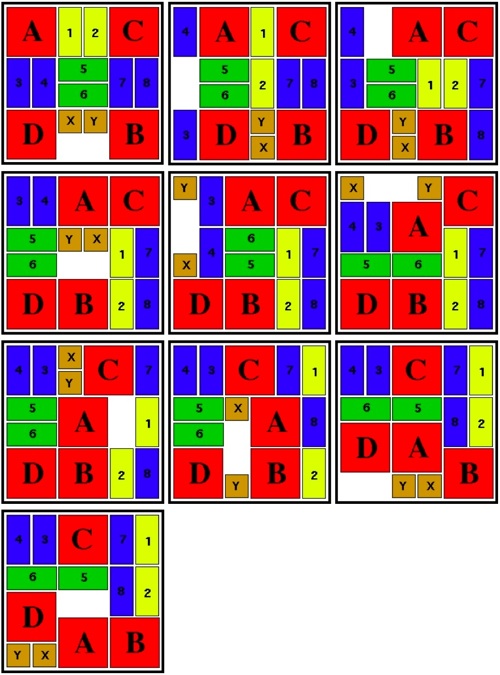
Hordern's book presents a 51 rectilinear move solution. Here are the start, every fifth position, and the end position of a 51 rectilinear move solution (54 straight-line moves):
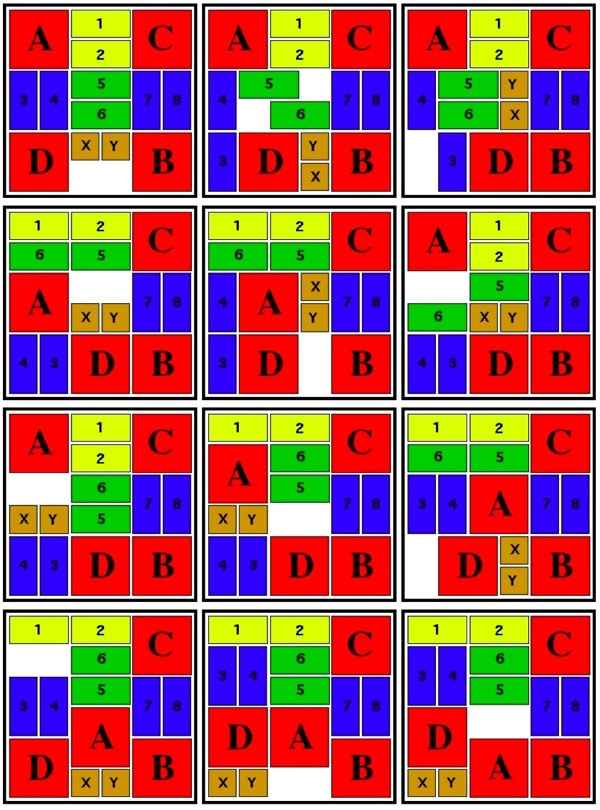
Hordern's book presents Model Garage A where both A,B and C,D must be exchanged, and Model Garage B that also requires that all other pieces end in their original positions, and gives the same 213 rectilinear moves (224 straight-line moves) solution for both, where the A version omits the last two moves of the B solution. Here are the start position and the position ending each row of the Hordern solution presentation:
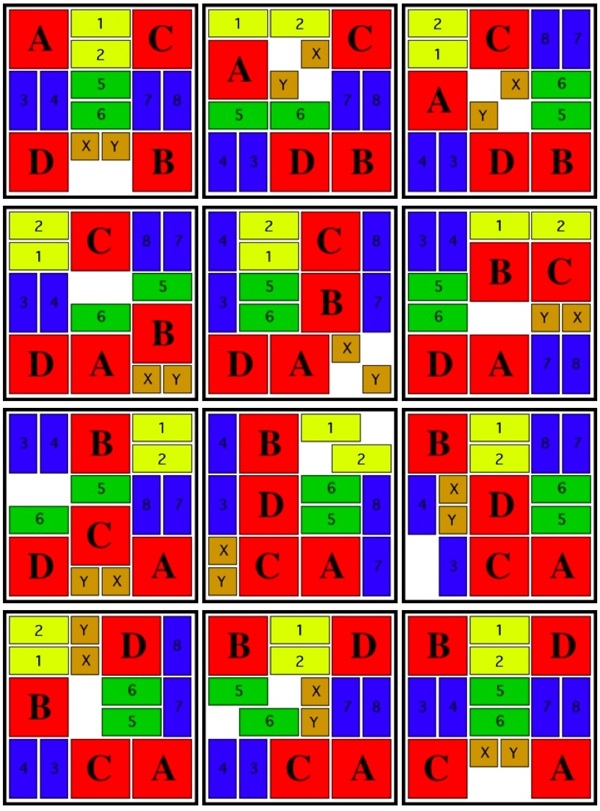
Slide A While Solution - 87 Straight-Line Moves (84 Rectilinear Moves)
Model Garage Solution - 51 Rectilinear Moves (54 Straight-Line Moves)
Model Garage A Solution - 210 Rectilinear Moves (222 Straight-Line Moves)
Model Garage B Solution - 212 Rectilinear Moves (225 Straight-Line Moves)
Model Garage B Solution - 224 Straight-Line Moves (213 Rectilinear Moves)




Designed by Nob Yoshigahara 1995, Rush Hour by ThinkFun.
(Tokyo Parking, wood tray and 16 wood pieces in cardboard box, 5.8" x 5.8" x 1";
Rush Hour, Plastic tray and 16 plastic pieces with storage bag, 6" x 5.5" x 2")
Rush Hour began with a license to Tokyo Parking, which comes with 36 problems. The Rush Hour problems are on cards in a tray that slides out of the front; four more problems are added for a total of 40 cards, where each has a solution on the reverse side. Each problem uses a subset of the pieces. The goal is to slide the pieces so as to be able to slide out a designated piece (the dark block in the Tokyo Parking directions or the piece labeled X on the Rush Hour cards) through gap on the right side of the tray. Pieces may only move in the direction of their longest dimension (that is, thinking of the pieces as vehicles, they can only move forward or in reverse); the Rush Hour tray has tracks that enforce this rule.
Rush Hour has been made in a number of variations, including metallic pieces, more problem cards, railroad cars, a junior version, and different packaging. Problem 36 of Tokyo parking is the same as problem 40 of Rush Hour (with a solution of 51 moves).
Further Reading
Rush Hour History, from: http://www.thinkfun.com/microsite/rushhour/creation
Tokyo Parking problem 36 (Rush Hour problem 40) can be solved in 51 straight-line movements; here is a diagram of the starting position, and the pieces at the finish:
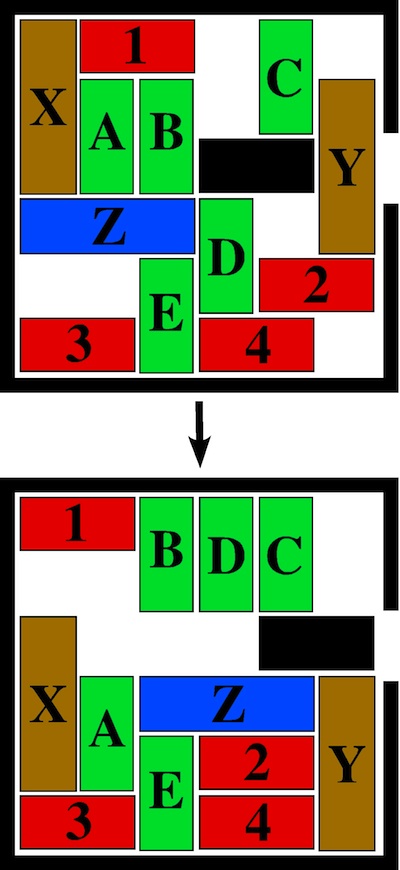

Designed and made by Minour Abe, circa 1985.
(cardboard box 4+58" x 4+5/8" x 3/4", wood tray, 8 wood pieces, and yellow keeper)
Starting with the pieces positioned as on the left below, slide them to correctly make the cow:
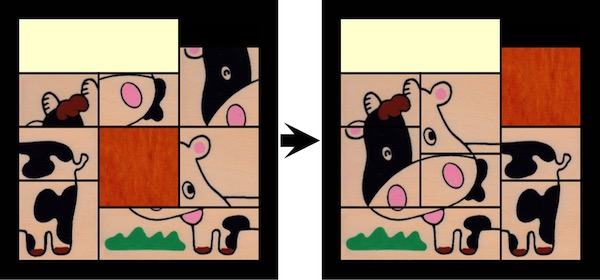
A somewhat tricky solution to start with is made more difficult because it is cumbersome at first to keep track of where pieces need to go when they are portions of a drawing rather than plain colors. The follow page shows a solution of 39 moves rectilinear moves (equivalent to 45 straight-line moves).

Designed and made by Nob Yoshigahara, circa 1985.
(cardboard box 4.75" x 6.5" x 3/4" and wood puzzle 5+7/8" x 4+5/16" x 9/16";
9 puzzle pieces and a green keeper piece to be removed;
box cover art added by J. A. Storer)
Here is a second one, with the pieces removed on the right:


The problem is to exchange PINK and BLUE (a smaller version of the Adam & Eve puzzle). The "police" piece in the center row is a bit wider than the others so as to not fit through the slots:
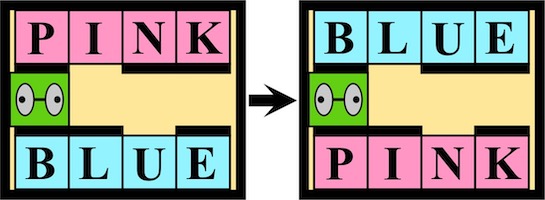
Here is a 44 rectilinear moves solution (corresponding to 104 straight-line steps):

Here is the 44 rectilinear moves solution of the preceding page in text format:


a.k.a. Comic Scramble Game
Designed by Nob Yoshigahara 1997, made in Japan.
(cardboard box, wood board, and 11 wood pieces, 6+3/4” x 5+5/8” x 3/4";
instructions ask for a solution of fewer than 57 moves; the following page shows 56 moves)
Here is every 7th move in a 56 rectilinear (130 straight-line) moves solution.


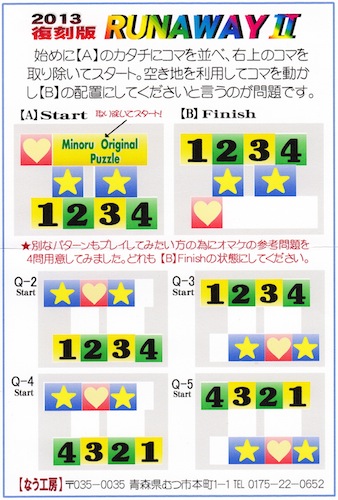
Designed by Minoru Abe, purchased 2013.
(cardboard box 4.3" x 5" x 7/8", wood tray, 7 wood pieces and wood keeper;
from the same designer as the RunAway puzzle)
All pieces are square except the large star is 4/3 wider than the others. The tray is arranged in three rows, where the top and bottom rows are each 4 units wide, but the top row is shifted 1/3 unit left with respect to the bottom row. The middle row has a one unit area, shifted 1 unit from the left edge of the top row, and a 4/3 unit area shifted 1/3 unit from the right of the top row (leaving 1/3 unit between the two areas).
The directions give 5 problems that have rectilinear solutions of 92, 73, 96, 38, 100, moves respectively. Here are the first, every 10th, and last position of a 92 rectilinear (111 straight-line) moves solution to problem 1:
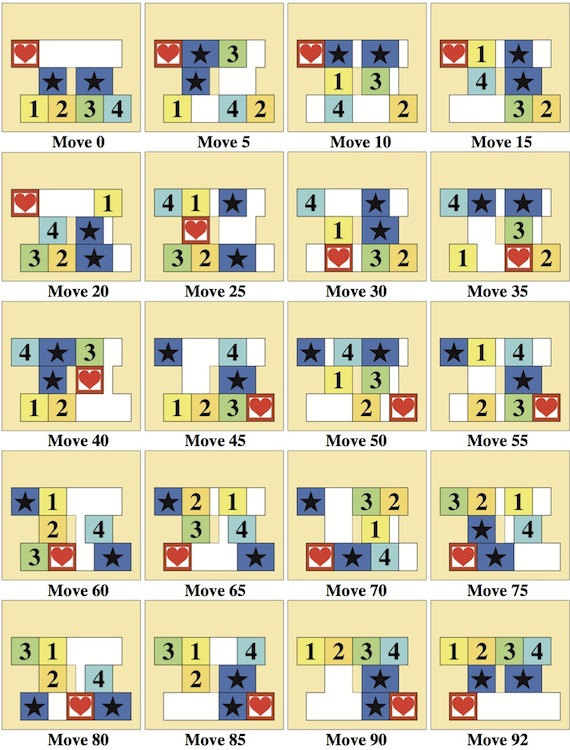

Designed and made by Minoru Abe, circa 1985.
(cardboard box 4+7/8" x 4+7/8" x 3/4", wood tray and 10 pieces, wood keeper and directions)
As shown in the directions on the left below, two 1/2x1 pieces and the 1x2 piece between the N and U are glued to the tray, and cannot move. Remove the 2x2 keeper piece and slide the pieces so as to exchange PINK and BLUE, leaving the blank 1x1 piece back in its original position:

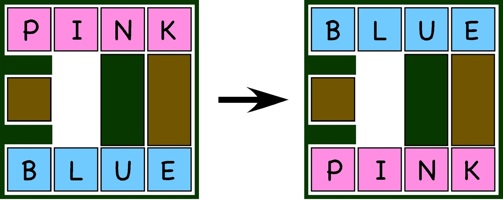
The following pages show a solution of 190 moves.

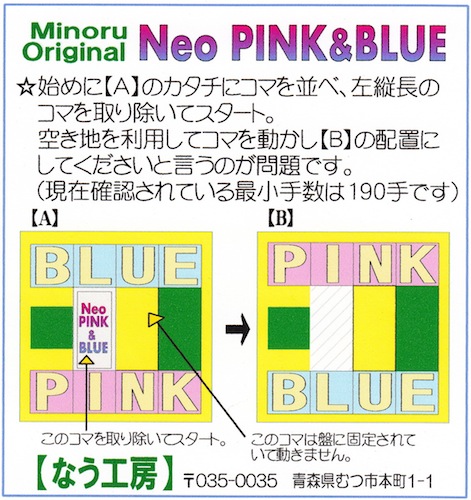
Made in Japan 2013.
(cardboard box 4.3" x 4.3" x 7/8", wood tray, 10 wood pieces and wood keeper)

Designed by Minoru Abe, made in Japan 2013.
(cardboard sleeve, Cherry tray, fixed 1/2x1's and 2x1 painted green, Oak PINK,
Bloodwood BLUE, Cocabola 1x1 & 2x1, black plexiglass keeper, 5"x5"x3/4")
Here is the starting position, every 8th step, and the final position of a solution of 190 rectilinear moves (233 straight-line moves):

(one rectilinear move = slide one piece along a rectilinear path)

a.k.a. Spirit of '76, Wooden Puzzle, Rectangle Puzzle
Patented by C. L. A. Diamond, 1927.
(orange cardboard box and 9 wood pieces, 4 by 4 by 1/2 inch)
Starting with the position shown below, slide the pieces so that the two L's form a 3 high by 2 wide rectangle in the upper right corner. Described on pages 16-17 of the 1942 Filipiak book (which presents a 56 move solution). Hordern's book presents a 23 rectilinear moves (26 straight-line moves) solution and two variations: make a rectangle from the two L's anywhere (19 rectilinear moves / 22 straight-line moves) and make a 2 high by 3 wide rectangle in the upper right corner (37 rectilinear moves / 41 straight-line moves).


Made by Harlekin, Germany, circa 2000?
(cardboard box, wood tray, and 9 wood pieces, 4 by 4 by 1 inch)
The booklet that comes with this puzzle gives the simplier problem that is also addressed in Hordern's book, of making a rectangle from the two L's anywhere (19 rectilinear moves corresponding to 22 straight-line moves); here is the solution given:





"MANUFACTURED BY THE STANDARD TRAILER CO. CAMBRIDGE SPRINGS, PA."
(blue / light blue / red / orange cardboard box and 9 wood pieces, 4" x 4" x 1/2")
The Standard Trailer versions of Ma's Puzzle on the previous page have various things written in the box. Inside the box lid the red and orange ones have a solution, whereas the blue and light blue ones invite you to send ten cents for one. Also, on the bottom, under the pieces, the blue and light blue ones advertize The Flying Puzzle and Dad's Puzzle:





"DISTRIBUTOR BONA FIDE BROOM &NOVELTY CO. PACOMIMA, CALIF."
(blue / light blue cardboard box and 9 wood pieces, 4 by 4 by 1/2 inches;
the label shown above is glued to the inside of the blue box top)
The Bona Fide Broom version of Ma's Puzzle on the previous page (blue box) has this label on the inside of the top cover:







a.k.a. Dad's Puzzler + Ma's Puzzle
Standard Trailer Co., Cambridge Springs, PA,
Dad's copright J. W. Hayward 1926, Ma's patented C. L. A. Diamond, 1927.
(cardboard box 4+1/4" x 5+1/8" x 1+5/8" containing
Dad's Puzzler 4" x 3.25" x 1/2" and Ma's Puzzle 4" x4" x 1/2")

Designed by Dick Hess 1980;
this puzzle made by J. A. Storer 2007
from a 1961 Adams Co. Dad's Puzzle and two plexiglass L-shaped pieces.
(cardboard sleeve, metal tray, and 8 plastic / plexiglass pieces, 3.75" x 3" x 5/16")
Hordern's book presents the following solution of 28 rectilinear moves (corresponding to 33 straight-line moves). Shown below are each of the moves where an L piece moves. The basic idea is to swap the 1x1 piece with the piece below it and then from Step 10 move the 1x1 piece to the lower right corner (Step 14) before trying to bring the L's together. Note that the only other possible final position can be achieved by modifying this lower right solution to have step 28 move an L up rather than down.



a.k.a. Tit-Bits Teaser No. 4
Patented 1928.
(cardboard box and 14 wood pieces, 4 by 4.75 by 1/2 inches;
box graphics are the same except that
the yellow one says "CAN YOU DRIVE THE CAR HOME?",
and the white one has "ORIENTAL ARTS CO." label on the box bottom)
The inside of the box lid of the Traffic Jam Puzzle shows 12 starting positions, where the goal is always to get the 2x2 to the lower right corner.

In the 1928 Babcock patent, the figures show problems 3 and 4, Claim 1 addresses puzzles of this type, and Claim 3 specifies this particular piece set. Hordern's book says this was also patented in the U.K. in 1930 (Tit-Bits Teaser No. 4), and presents solutions for the 12 problems of rectilinear (straight-line) moves:
43 (51) 52 (61) 58 (67) 60 (69) 57 (64) 73 (85) 75 (89) 99 (115) 80 (94) 128 (150) 132 (147) 223 (257)

Tit-Bits Teaser No. 4, George Newnes Ltd., London, 1931.
(cardboard box and 14 wood pieces, 4 by 4.75 by 1/2 inches;
text at top of box top says "COMPETITION CLOSES FEB. 28th 1931";
text at bottom of box top says "MADE IN U.S. A.")
Tit-Bits Teaser No. 4 is puzzle number 11 of the Traffic Jam puzzle. Hordern's book gives both a 132 move rectilinear move solution and a 147 move straight-line solution. Here is the 132 move solution that came with the puzzle:
Hordern's book credits this puzzle as manufactured by Dr Hex Association, USA, 1930s. It uses the same piece set as Traffic Jam (where one of the 2 unit pieces is oriented vertically), also uses a 5 by 6 unit tray, and has the same goal of moving the 2x2 piece to the lower right corner. Here is the starting position; the upper left corner is called "Detroit" and the lower right corner is called "Washington":
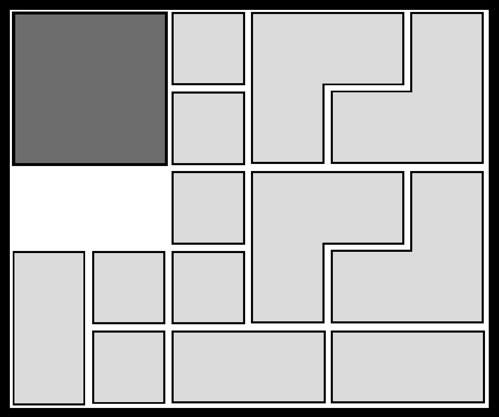
Further Reading
Babcock Patent, from: www.uspto.gov - patent no. 1,683,014
Designed Naoyuki Iwase circa 2012
(wood tray with 8 pieces, 4 inches square by 1/4"thick)
Below is the problem shown on the puzzle directions.
The fit of this puzzle is sufficiently loose that it can be solved by rotating and manipulating pieces in a non-rectilinear fashion, but a soution using rectlinear movement is also possible. The following page presents a 32 rectilinear moves solution.
Here is a 32 rectlinear moves solution:
Designed Naoyuki Iwase circa 2014
(wood tray with 9 pieces, 4 inches square by 1/4"thick)
Below is the problem shown on the puzzle directions.
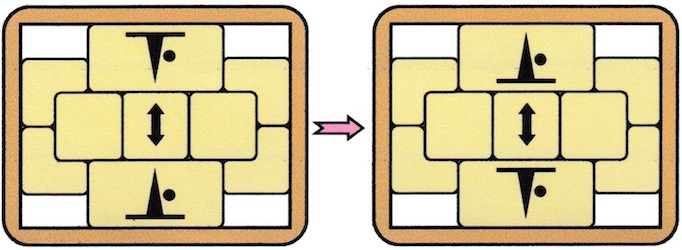
The fit of this puzzle is sufficiently loose that it can be solved by rotating and manipulating pieces in a non-rectilinear fashion, but a soution using rectlinear movement is also possible. The following page presents a 103 rectilinear moves solution.
Here is every third step of a 103 rectlinear moves solution:
Designed by Jerry Loo, made by Eric Fuller, 2016.
(Maple, Mahogany, Walnut, Acrylic, 6" x 3.75" x 3/4";
removable acrylic cover has starting position etched on it)
Exchange pieces A and B and finish with the other pieces in their original positions. Below are selected steps, including every step in which piece X moves, of a solution of 33 rectilinear steps (53 straight-line steps, 74 unit steps). Note that at step 22 pieces A and B are exchanged, and the remaining steps put the other pieces back.


Designed and made by Diniar Namdarian 2013; sleeve made by J. A. Storer.
(Laser cut plastic three layers, 3.75" x 6.75" x 3/8";
thickness are base 1/8", tray edge 1/8", pieces 1/8" back with 1/8" figures)
Problem 1: Exchange the clouds and sheep; here are every 7 steps of a 96 rectilinear steps, 114 straight-line steps solution (108 straight-line steps, are also possible):
Problem 2: Also exchange the rabbit and the sun; here are every 9 steps of a 113 rectilinear steps, 131 straight-line steps solution (130 straight-line steps, are also possible):



a.k.a. Hole In One, Idol Plays Slide Puzzle
Left "Slider" circa 2000, center "Hole In One" circa 2007, right "IdolPlays" circa 2024.
(Slider has aluminum tray and 5 aluminum pieces, 3.25 by 4.5 by 3/4 inches,
Hole In One has wood tray and 5 wood pieces, 4.5 by 6 by 1.25 inches,
Idol Plays has plastic tray and 5 plastic pieces, 4.25 by 6.25 by 3/8 inches,
directions added by J. A. Storer to Slider box top and Hole In One box bottom)
Idol Plays used in the show Survivor, sleeve made by J. A. Storer from its directions.
Move the 2x2 square inside the square surrounded by the four corner pieces. It can be solved in 22 moves. Here is the solution that came with Slider:

Designed by Minoru Abe, this one made by J. A. Storer, 2010.
(Walnut tray, Cherry L's, Bloodwood square, 4.4" x 6.5" x 3/4")
Move the square from outside to insdie the L's. Here is the start and every other position of a 28 rectilinear moves (33 straight-line moves) solution:

Designed by Ed Pegg Jr.;
this puzzle made by J. A. Storer 2007
from a 1961 Adams Co. Dad's Puzzle and two plexiglass L-shaped pieces.
(cardboard sleeve, metal tray, 6 plastic / plexiglass pieces, 3.75 x 3 x 5/16 inches)
From the starting position shown below, move the bottom 1x2 piece to the top (i.e., float the soap). Baxter's page on Pegg puzzles lets you play this game and indicates a minimal solutin of 43 rectilinear moves.
Further Reading
Baxter's Pegg Page, from: http://www.johnrausch.com/SlidingBlockPuzzles/pegg.htm


Designed by Minoru Abe circa 1985, this puzzle made by J. A. Storer 2007.
(cardboard sleeve, wood tray, plexiglass keeper, and 9 wood pieces, 6" x 7" x 3/4",
tray cherry, 2x2 walnut, L's purple heart, 1x2's bloodwood, 1x1's rosewood,
sleeve shows 45 problems - 12 on top and the remaining 33 on the bottom)
Starting from various positions on the 6 by 4 unit tray, the goal is to move the 2x2 piece to the top. The two 1x1 pieces painted black are glued to the tray and cannot move. The following page show a variety of starting positions; of these positions 17, 20, 32, 35, 40, and 45 are symmetric ones; here they are in increasing order of the number of rectilinear moves required, along with six examples of non-symmetric positions:
Problems 1 through 20 are on the Minoru Abe directions, 21 to 29 are problems D28, D29, D30, D32, D33, D34, D38, D39, D41 from pages 113-116 of the Hordern book (problems D24, D25, D26, D27, D31, D35, D36, D37, D40, D42, D43 correspond to problems 1, 6, 3, 12, 5, 11, 4, 13, 10, 15, 19), 30, 31, 32 are the three Henderson problems shown on the Fujiwara page, and 33 to 45 are Fujiwara's problems 1, 3-10, 12-15 (the Abe problems A-D shown on that page correspond to problems 13, 14, 12, 11, and Fujiwara problems 2, 11 correspond to 20, 17).

Designed by Minoru Abe 1979, purchased in Japan 2010.
(wood pieces ina cardboard box, 6" x 4.4" x 7/8")
Here is a 26 rectilinear moves (35 straight-line moves) solution to the first of the problems in the Abe directions:
Here is a 28 rectilinear moves (39 straight-line moves) solution to the second of the problems in the Abe directions:
Here is an 87 rectilinear moves (117 straight-line moves) to the last of the problems in the Abe directions (it can also be done in 115 straight-line moves that are equivalent to 89 rectilinear moves):

Further Reading
Fujiwara's Pages, from:(first) http://www.pro.or.jp/~fuji/java/puzzle/slide/V2.0/block10-eng.html
(second) http://www.pro.or.jp/~fuji/java/puzzle/slide/V2.0/block10.html


Designed and made by Minoru Abe, circa 1985.
(cardboard box 7+7/8" x 5.5" x 3/4" with
wood tray and 15 wood pieces, 7+7/16" x 5+1/8" x 9/16")
The puzzle has these pieces (a second red T-piece is a keeper piece to be removed):

The directions give four starting positions for the problem of moving the red T-piece to the top:
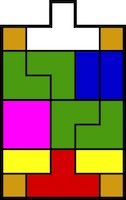
Problem 1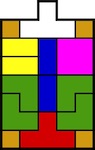
Problem 2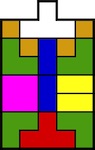
Problem 3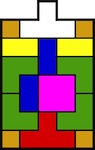
Problem 4
These four problems do not place any constraints on the other pieces of a final position. Here we also consider what we refer to as Problem 2A, which amounts to moving up the T-piece together with the two squares next to it and dropping down the remainder of the starting position:
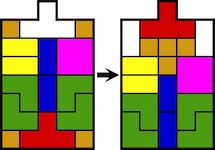
Here is every other step of a solution of 104 rectilinear moves for Climb 15 problem 1:
Here is every third step of a solution of 132 rectilinear moves for Climb 15 problem 2:
Here is every third step of a solution of 173 rectilinear moves for Climb 15 problem 2A:
Here is every other step of a solution of 101 rectilinear moves for Climb 15 problem 3:
Here is every third step of a solution of 148 rectilinear moves for Climb 15 problem 4:

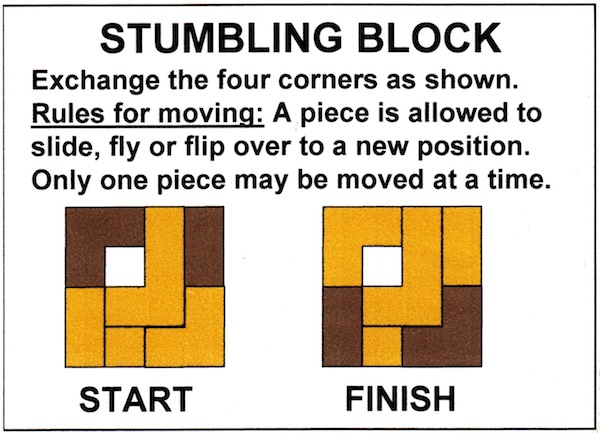
Designed by Dick Hess and made by Walt and Chris Hoppe 2010.
(wood pieces in a cardboard box 5.3" x 3.8" x 7/8")



Designed by Dick Hess and made by Walt and Chris Hoppe 2012.
(wood pieces in a cardboard box 5.3" x 3.8" x 7/8",
with two additional bottom cards and problem / solutions sheet)

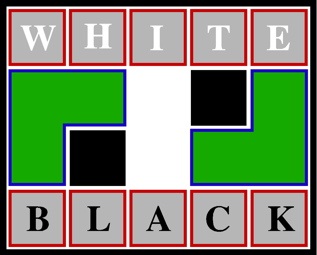
Designed and made by Minoru Abe 1985, directions in Japanese.
(cardboard box, wood tray, and 12 painted wood pieces, 5.25 by 6.25 by 3/4 inches)
The two blank 1x1 pieces are glued to the tray and cannot move. The center blank 2 by 1 keeper piece is removed to make the starting position shown on the right above. The goal is to slide the pieces so that BLACK is on top and WHITE is on the bottom.
Hordern's book shows 198 rectilinear (237 straight-line) moves and the Puzzler's Tribute book, in a chapter coauthored by Minoru Abe, shows 190 rectilinear (231 straight-line) moves.
Here are the start position, end position, and the positions of Hordern's solution for which an L-shaped piece is to be moved next:

We use a more verbose notation than Hordern's book. The first letter is the piece to be moved (X denotes the left L-shaped piece and Y the right one) and the second letter is the direction; all moves are a distance of 1 unit unless followed by a 2 (to specify two units). Two consecutive moves of the same piece are listed together as a single rectilinear move.
(198 rectilinear moves, 237 straight-line moves)
Here are the start position, end position, and the positions of Puzzler's Tribute solution for which an L-shaped piece is to be moved next:

We use the same notation as we did for the Hordern solution (like Hordern's book, the Puzzler's Tribute book uses a more compact notation than is used here). The first letter is the piece to be moved (X denotes the left L-shaped piece and Y the right one) and the second letter is the direction; all moves are a distance of 1 unit unless followed by a 2 (to specify two units). Two consecutive moves of the same piece are listed together as a single rectilinear move.
(190 rectilinear moves, 231 straight-line moves)
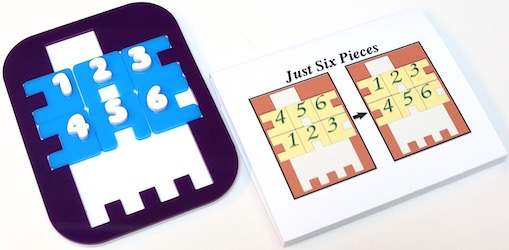
Designed and made by Diniar Namdarian, 2016; sleeve made by J. A. Storer.
(laser cut plastic, 5.5" high by 4.25" wide x 3/8" thick)
Exchange 4-5-6 with 1-2-3. A 41 rectilinear moves (73 straight line moves) solution is possible, and the puzzle directions show a 41 moves solution, every 3rd of which is shown here:

Designed by Minoru Abe, purchased 2012.

(cardboard box, wood tray, 5 wood pieces, and wood keeper, 4.4" x 5" x 7/8")
Pieces are 3 units square; all notches and protrusions are 1 unit square. With the keeper removed, exchange pieces 1 and 2 and exchange pieces 3 and 4. Here is the start, every 7th move, and the final position of a 35 Rectilinear moves (75 Straight-Line moves, 256 unit moves) solution:



Designed by Minoru Abe, circa 1985.
The directions are in the theme of the other Abe puzzles Solo and Egg Egg (a.k.a. Dinausaur Egg, Solo 2). It can be solved in 41 Rectlinear steps (94 Straight-line steps). Here is every third move:

Designed by Minoru Abe, purchased 2012.

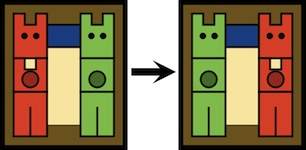
(cardboard box, wood tray, 7 wood pieces, and wood keeper, 5" x 4.4" x 7/8")
On the left and right, the top and bottom pieces are 4 units high by three units wide, and the middle pieces are 3 units square. The blue piece is 2 units high by 3 units wide. All notches and protrusions are 1 unit square. With the keeper piece removed, exchange the three pieces on the left with the corresponding three pieces on the right. Here is the start, every 7th move, and the final position of a 74 Rectilinear moves (108 Straight-Line moves, 308 unit moves) solution:


Designed By Minoru Abe, purchased in Japan 2010.
(wood, 10 moving pieces, one fixed piece, and keeper, 5" x 9" x 7/8")
At the top is a lizard from a 2-unit wide and three 3-unit wide pieces. At the bottom is a lizard from a 2-unit wide piece, a 3-unit wide piece, a 2-unit wide piece, and a 4-unit wide piece. On the left is a 2-row high by 2-unit wide piece. In the middle row, two units from the left, is a 2-unit wide piece glued to the bottom. On the right is a 2-row high L-shaped piece has a 2-unit wide top and a 4-unit wide bottom. Here is the start, every 8th, and the final position of an 85 rectilinear moves (109 straight-line moves) solution to exchange the lizards:

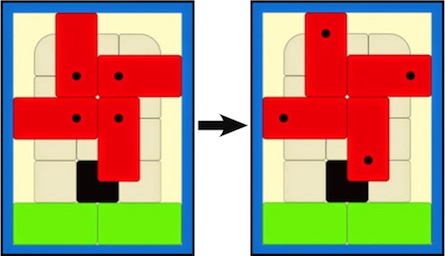
Designed by Serhiy Grabarchuk and made by Diniar Namdarian 2016; sleeve by J. A. Storer.
(laser cut plastic, 4.75" x 6.25" x 3/8" thick) Rotate the windmill 90 degrees clockwise.
A two layer puzzle with the red pieces on the upper layer, each of which is a rectangle 4 units long and 2 units wide. In addition to the two 1x1 gray pieces, the 1x1 black piece, and the two 2 x 4 green pieces, the bottom layer has four identical shaped 2 units wide by 4 units long gray pieces, each with a red piece attached to in centered and perpendicular. All four of these gray pieces have one corner that is a circular arc, where three of those arcs can be seen in the starting position, and the fourth arc on the piece under the lower right red piece is facing up and to the right, hidden under the lower left red piece.
A 66 rectilinear moves (90 straight-line moves) solution is possible, and the puzzle maker directions show a 66 moves solution, shown on the following two pages.



Designed by Serhiy Grabarchuk, Ukraine, purchased from Bits And Pieces 2007.
(wood tray and metal pieces, 3.75 by 4.25 by 1/2 inches)
Slide the pieces to solve the Double Square puzzle; the start and end positions are shown above. Here is the solution sheet that was sold with the puzzle:

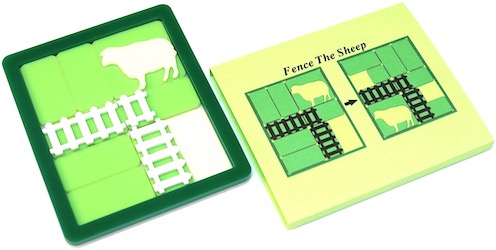
Designed and made by Diniar Namdarian, 2016; sleeve made by J. A. Storer.
(laser cut plastic, 5.75" high by 4.75" wide x 3/8" thick)
A two layer puzzle where the left end of the 1x2 horizontal fence is attached to a 1x1 piece below (and the right end sits above a 1x1 piece), the 1x1 fence sits on top at the left end of a 1x2 piece, and the 2x1 vertical fence sits on top at the upper end of a 2x1 piece.
The problem is to move the sheep inside the fences:
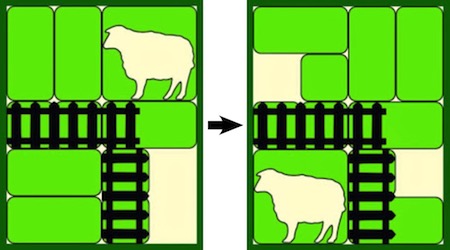
The puzzle directions give a 168 moves solution; the following pages show the details of a 168 rectilinear moves solution.
The puzzle directions also note that an easier puzzle may be constructed by having the 1x1 fence sit on top of a 1x1 piece (and to the right of that piece is another 1x1 piece), and provides a 70 moves solution; the following pages show the details of a 70 rectilinear moves solution.
In the solutions to follow, for each position, the bottom layer is to the left of the vertical row of $'s, and the top layer is to the right. For example, here are steps 0 to 3 of the Fence The Sheep solution:

Here is every 3rd step of a 168 rectilinear moves (178 straight-line moves) solution.
Here is every 2nd step of a 70 rectilinear moves (87 straight-line moves) solution.

Designed and made by Diniar Namdarian, 2016; sleeve made by J. A. Storer.
(laser cut plastic, oval 4+1/8" high by 7.5" long x 3/8" thick)
Two layers, where the butterflies are attached to single squares going down the diagonal below; the upper blue is attached to position (1,1), the lower blue is attached to position (2,2), the upper green is attached to position (3,3), and the lower green is attached to position (4,4), and the problem is to exchange the butterflies. A 52 rectilinear moves (68 straight-line moves) solution is possible; here is every 4th step of a 52 moves solution shown in the puzzle directions.

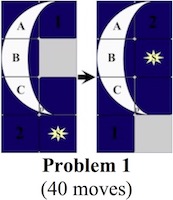
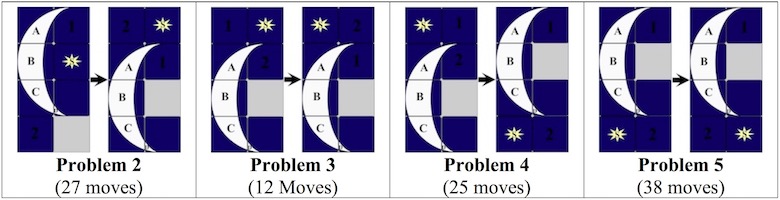
Designed and made by Diniar Namdarian, 2016; sleeve by J. A. Storer.
(laser cut plastic, 3+9/16" x 6+3/8" x 3/8" thick)
A two layer puzzle where the top tip of the moon overlaps (but is not attached to) the square next to it (and the raised tray edges prevents that tip from overlapping edges). Here are steps 1 through 40 from solutions provided by the puzzle directions for Problem 1:

In the solutions to follow, for each position, the bottom layer is to the left of the vertical row of $'s, and the top layer is to the right. For example, here are steps 0 to 2 of Problem 1 solution:

Starting with Step 2, here is every second step of a 40 moves solution:
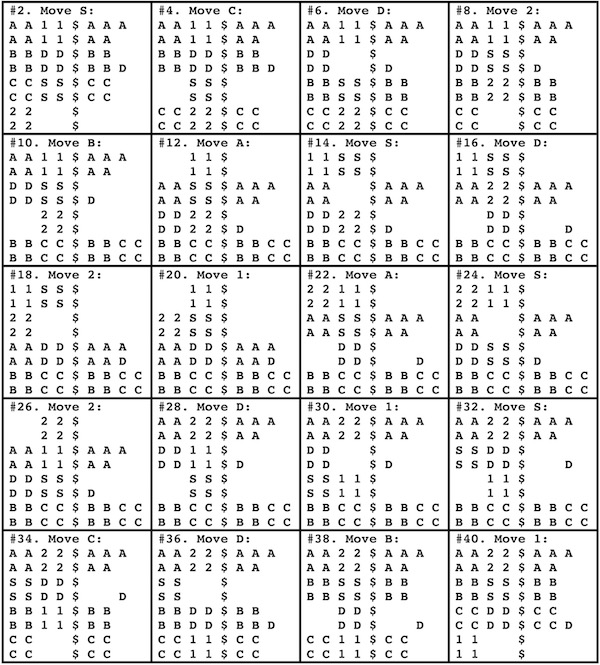
Here is every second step of a 27 moves solution:
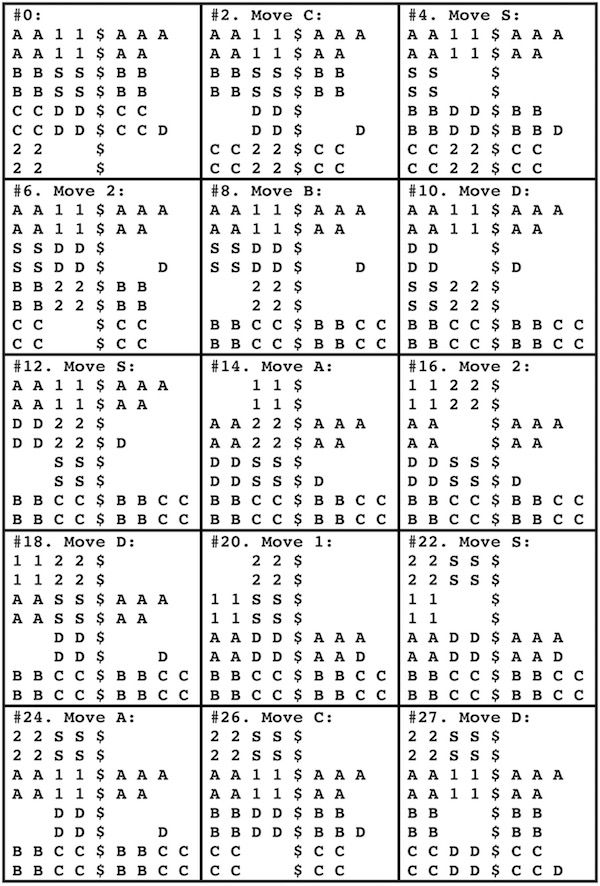
Here is a 12 moves solution:
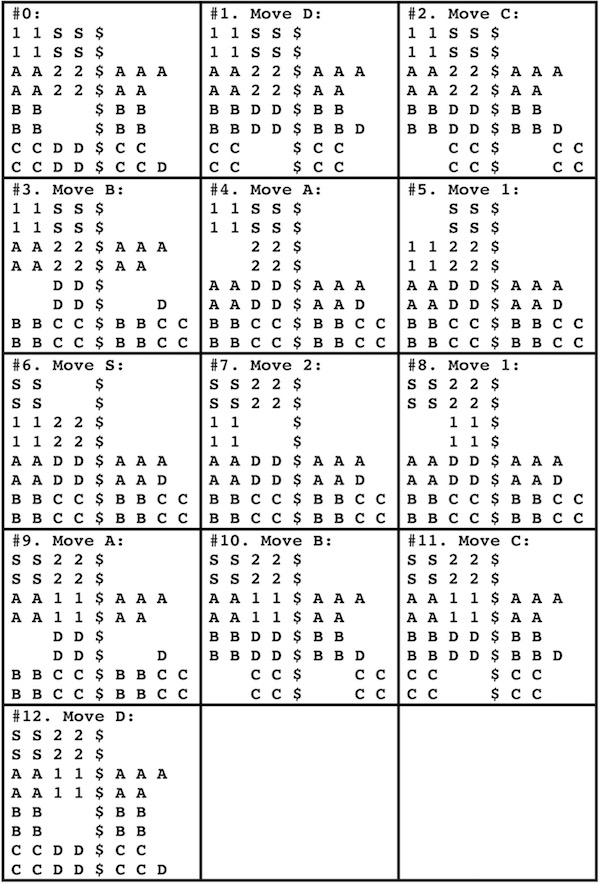
Here is every second step of a 25 moves solution:
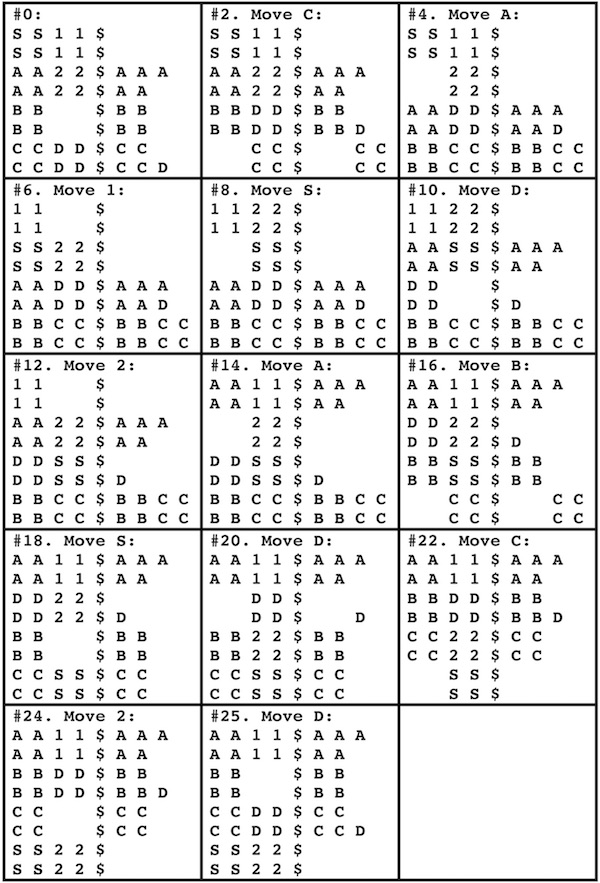
Here is every second step of a 38 moves solution:
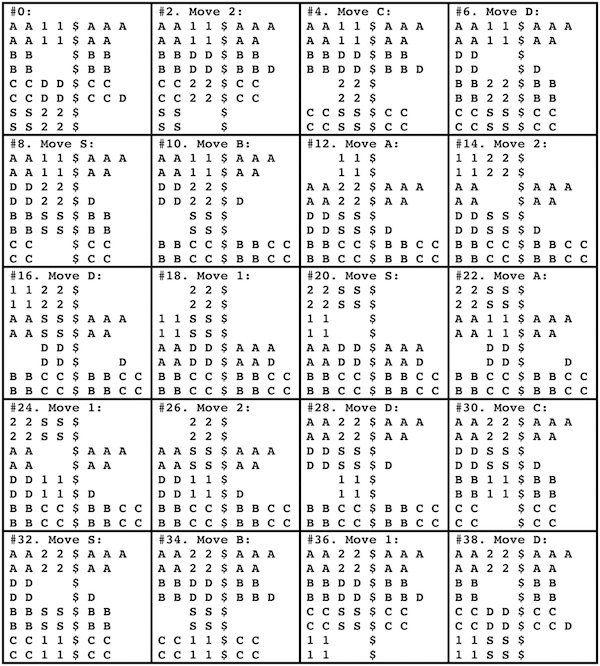


Designed and made by D. Namdarian 2013; sleeve added by J. Storer.
(made from 1/8" thick laser cut plastic, board 2 layers, pieces 2 layers, 4.3" x 5.5" x 3/8")
Looks like the classic Get My Goat puzzle, but the pieces are composed of two layers. The puzzle comes with a solution sheet showing a 70 move solution. The following page shows every fifth move of a 69 move solution that starts with the same first 19 moves.


Designed and made by D. Namdarian 2013; sleeve added by J. Storer.
(made from 1/8" thick laser cut plastic, board 2 layers, pieces 2 layers, 4.3" x 5.5" x 3/8")
The top layer has a blue egg on the left and a green egg on the right, each formed from three sections, arranged as two curved pieces side by side each occupying a 2 high by 1 wide space, sitting on top of a curved piece that occupies a 1 high by 2 wide space. The goal is to exchange the two eggs. Each of the six of the top layer egg sections occupies a 2 unit region of the top layer and has one of its halves glued to a 1x1 white piece on the bottom layer. The remainder of the bottom layer consists of 5 free moving 1x1 white pieces and one empty 1x1 region. As the pieces slide, portions of the top layer may slide over the free 1x1 pieces on the bottom layer. They may also slide over the rim of the puzzle. So although the board is based on a 3 by 4 grid, the top layer moves around what is effectively a 5 by 6 grid.
The following pages show the solution sheet that came with the puzzle which presents a 78 move solution. The moves of the free 1x1 pieces on the bottom layer can be achieved by pushing on the exposed portion of the piece or combining two moves by pushing on the top layer and dragging a 1x1 free piece below, with the exception of Moves 10 and 18. Move 10 can be overcome by combining Moves 10 and 11 so that the piece of Move 11 pushes the piece of Move 10 as it moves. Move 18 may require one to cheat just a little by lifting the blue egg section that covers the free 1x1 piece below it in the bottom row.
On the following pages, after the puzzle solution sheet, is shown a different sequence of moves that can be taken after move 58 to lead to a shorter solution of 74 moves.
It seems reasonable that when a top layer piece covers a free moving bottom 1x1 square that the two can move together to count as one move, in which case the solution sheet sequence can combine moves 4+4, 6+7, 13+14, 29+30, 34+35, 46+47, 48+49, 50+51, 62+63, 74+75, to reduce the total move count from 79 to 69. Or, the 74 move solution can combine moves 4+4, 6+7, 13+14, 29+30, 34+35, 46+47, 48+49, 50+51, 62+63, 72+73, to reduce the total to 64 moves.


Designed and made by D. Namdarian 2015; sleeve added by J. Storer.
Problem 1
Probllem 2
Problem 3A
Problem 3B
(made from 1/8" thick laser cut plastic, board 3 layers, pieces 2 layers, 4.375" x 6.75" x 3/8")
As shown in the figure on the upper right above, there are 14 unit square white pieces that slide on the lower layer, where some of them have portions of the red upper layer glued to them. The puzzle came with two trays, an easier tray that has a simple border, and a harder tray that has triangles on the upper left and lower right of the border that allow the bottom white layer of pieces to slide underneath. The directions describe Problems 1, 2, and 3A, where for all three of these, it makes no difference if the harder puzzle tray is augmented to also have a triangle in the upper right corner. Problem 3A differs in style from Problems 1 and 2 in that the blank square starts in the upper right but ends up in the upper left. Problem 3B is an additional problem where, like Problems 1 and 2, the empty square starts and ends in the upper right.
Solutions are as follows:
Easy tray:
Problem 1: 30 moves
Problem 2: 60 moves
Problem 3A: 24 moves
Problem 3B: 32 movesHarder tray:
Problem 1: 30 moves
Problem 2: 66 moves
Problem 3A: 24 moves
Problem 3B: 32 moves

Designed and made by D. Namdarian 2013; sleeve added by J. Storer.
(4 layers of laser cut plastic, 6.75" x 4.8" x 1/2")
Move the football from right to left goal square, where it can be carried in the square of a white player piece. Ignoring layers, here are selected positions of a 35 rectilinear (40 straight-line) moves solution (it goes to player Q at position 18 and is passed to player P at position 31):
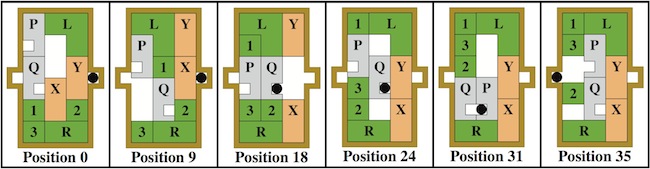
Taking layers into account, layer 1 underlies the whole puzzle, layer 2 forms the rim around it and has the bottom layer of the pieces, layer 3 has the ball and the top layer of the pieces, and layer 4 is decorative showing players. Here are selected positions of a 61 rectilinear (72 straight-line) moves solution where the ball never leaves layer 2 by only moving directly between two abutting squares (it goes to player Q at position 35 and is passed to player P at position 55):
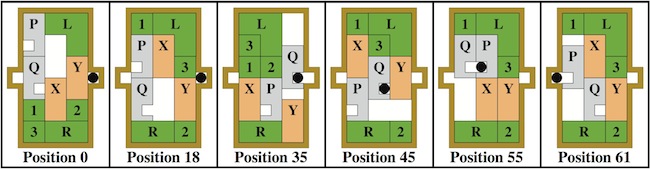
For a second problem given with the puzzle directions, here are selected positions of a 75 rectilinear, 84 straight-line moves solution (the ball goes to player Q at position 37 and is passed to player P at position 55):Football Match Problem 2 Alternate Solution
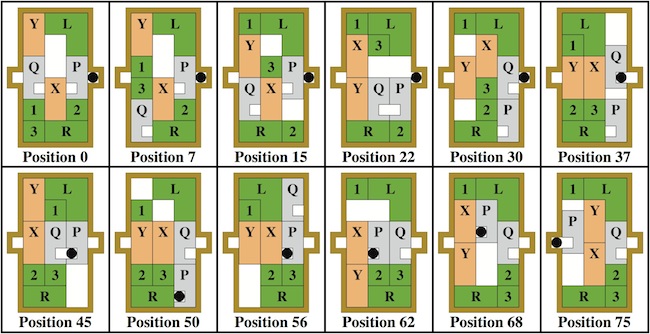
Here are selected positions of a 76 rectilinear, 83 straight-line moves solution to Problem 2 (the ball goes to player Q at position 50 and is passed to player P at position 70):
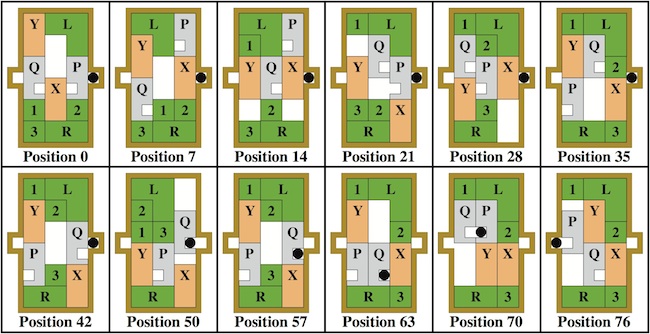
For a third problem given with the puzzle directions, here are selected positions of a 85 rectilinear (90 straight-line) moves solution (the ball goes to player Q at position 59 and is passed to player P at position 66):
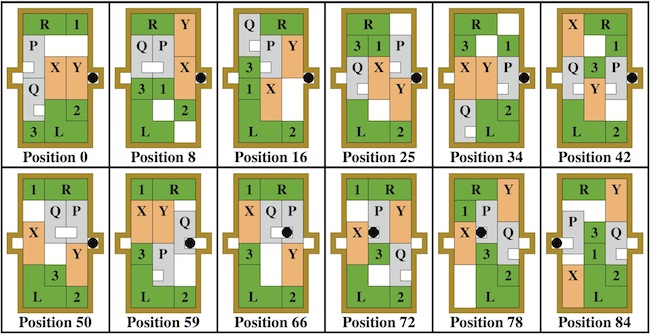

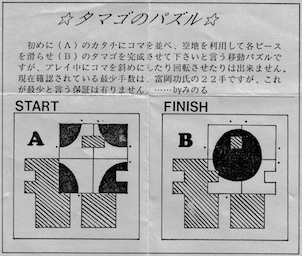
a.k.a. Dinosaur Egg, Dragon's Egg, Solo2
Egg designed and made by Minoru Abe, circa 1985.
(directions and wood tray with 5 wood pieces, 3" square; cardboard box by J. A. Storer)
After removing the brown keeper piece, the Egg puzzle is shown in the directions above and below, along with two other puzzles that we present here:
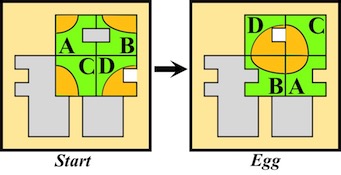
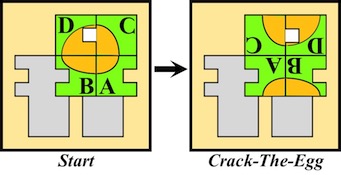
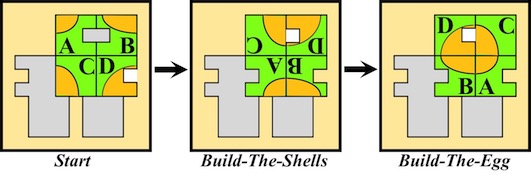
The puzzle geometry allows a piece to be rotated at any of locations 1, 2, 3, 4 as shown below, provided that there is sufficient unoccupied clear space below and next to it, and this ability allows a 13 moves solution (36 segments of either a straight-line move or rotation); rotations are at locations 1, 3, and 4 (an essentially identical solution rotates at locations 1, 2, and 4).
Unlike the Crack-The-Egg and Build-The-Egg problems, the basic Egg problem can be solved without rotations; here is a 22 moves (50 straight-line moves) solution:
Rotations are necessary to solve this problem. It is interesting to note that this can be done in 38 moves with rotations only in location 1, 38 moves with rotations only in location 2, or 23 moves with rotations only in location 3 (solving is not possible using only location 4 for rotations).
Here is a 15 moves solution (37 segments of either a straight-line move or rotation) that uses locations 1, 2, and 4 for rotations:
The second half of the problem, building the egg from the shell halves, can be done in 15 moves by reversing the Crack-The-Egg solution.
It is interesting to note that building the shell halves can be done in 30 moves with rotations only in location 1, 29 moves with rotations only in location 2, and 33 moves with rotations only in location 3 (solving is not possible using only location 4). Also, an interesting 22 moves solution does not rotate at location 4 and rotates piece A three times.
Here is a 14 moves solution (36 segments of either a straight-line move or rotation) to build the shell halves that uses only locations 3 and 4 for rotations; the last move of A can be combined with the first move of A in Crack-The-Egg reversed solution for a total of 28 moves.


Designed by Minoru Abe, purchased 2010.
(wood tray 4.5" x 4.5" x 3/4", 4 wood pieces, and wood keeper piece)
Here is the start position and every other step of the 22 rectilinear moves solution that does not use rotations, using photos from the puzzle:

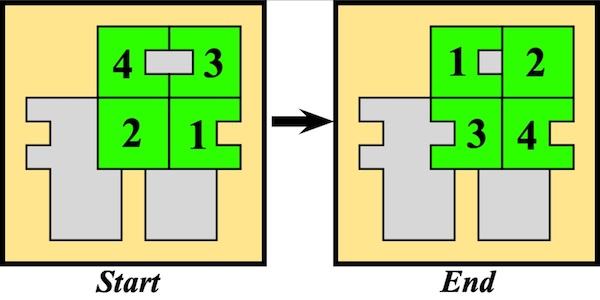
Designed by Minoru Abe, circa 1985.
The directions for this puzzle are identical as for the Egg puzzle, except there are no graphics on the pieces, just just numbers. The solutions presented for Egg work the same for this puzzle (substitute the labels 1,2,3,4 for A,B,C,D.

Designed and made by Diniar Namdarian, 2016; sleeve made by J. A. Storer.
(laser cut plastic, 3+3/8" high by 5.5" wide x 3/8" thick)
The directions ask one to exchange the upper left orange E with the lower right red E so that "ENJOY" is all red and "LIFE" is all orange:

In the theme of the Fifteen and Panama Canal puzzles, this is a seemingly impossible problem because of puzzle position parity; from any position, half of the other possible positions are reachable and half are not, and the start and end positions are in opposite halves.
However, there is sufficient free space in this puzzle to make moves that are not the straightforward movement of a piece left or right by a piece width or up and down by a piece height, and this allows two adjacent pieces to be exchanged (which reverses the puzzle parity).
The following pages show four ways to solve the puzzle, all of which fix the parity by effectively exchanging two letters that are adjacent to each other.
The first solution uses rotations to exchange L and I.
The other three solutions, using strictly rectilinear moves, move letters incrementally vertically; the first exchanges L and E, the second I and the orange E, and the third I and the red E.
We use E to denote the red letter E and e to denote the orange letter e.
1. Slide lifE right, e down, and N left to make:N . J O Y2. Exchange the l and i with non standard movement:
e l i f E1. L rotates 90 degrees clockwise and slides up.3. With parity reversed, 34 moves can finish the solution:
2. I slides left and rotates 90 degrees counter clockwise.
3. L rotates 90 degrees counter clockwise and fits next to J.
4. I rotates 90 degrees clockwise and slides left.
5. L slides down.
Here is a solution of 43 rectilinear moves (46 straight-line moves). Positions 23 to 30 change parity by exchanging L and E. Notice that moving e down in Position 22 gives a position identical to Position 30, except with L and E exchanged.
Here is another solution of 43 rectilinear moves. (48 straight-line moves). Positions 26 to 30 change parity by exchanging I and e. Notice that moving e up and then I left in Position 25, and moving I left in Position 30, gives identical positions except with I and e exchanged.
This solution shown here, from the puzzle directions, uses 43 rectilinear moves (48 straight-line moves). The red E is exchanged with I in steps 14 to 18 (in Step 18, if E is move up and I moved left, the position is identical to step 13 with I moved left and J moved up, except with I and E exchnaged).



Patented by F. G. Dustin 1935
Made by Diniar Namdarian 2019; sleeves made by J. A. Storer.
(laser cut plastic, left 5.25" x 4.75" x 3/8", right 4.75" x 4.75" x 1/4")
Looks like the Fifteen, puzzle at first, but except for 15, pieces are joined together in pairs. The blue puzzle on the left is the original described on page 151 of Hordern's book; the problem is to reverse the numbers, and it can be easily solved except for the 13-14 piece ending upside down, and then finishing as shown in the Dustin patent (below). The red puzzle has a slightly smaller interior space so as to not allow the Dustin solution (1,6,14,13,15 won't fit the diagonal); a 50 step solution of the puzzle maker to turn the numbers 90 degrees is on the following two pages.
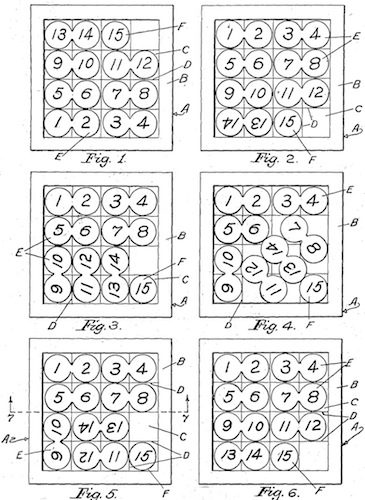

Further Reading
Dustin Patent,, from: www.uspto.gov - patent no. 1,993,211

Designed by Minoru Abe circa 2000; this one made by J. A. Storer 2012.
(1/4" thick aluminum turntable and maple plywood with Kingwood trim, 4x4x1/2 inches)
Remove the black keeper. Easy shown on the left below is to rotate the fruit; it can be solved in 226 rectilinear moves if a single move may pass through the turntable independent of its initial orientation, 250 rectilinear moves if both entering and leaving the turntable starts a new move, and 280 rectilinear moves if repositioning the turntable requires an additional move. On the right, which we call Tedious, is to cut the fruit; it can be solved in 302, 334, or 374, moves respectively.
Easy
Easy
These solutions never rotate the 1 2 pieces; below are key steps from the 302 rectilinear Tedious solution that can be viewed as two initial steps, followed by moving 1 2 from one side of the puzzle to the other a number of times to allow an exchange, followed by three final steps:
- From 1/4" thick maple plywood, cut the pieces.
- Make the piece graphics on a computer, print on glossy photo paper, cut them out, glue onto the pieces using a glue stick, and lightly sand to blend in the edges of the paper.
- Make the turntable piece; this one was made by roughing it out from 1/4" aluminum plate on a band saw, finishing on a lathe, drilling and beveling the hole, cutting the rectangle into it with a band saw, and then finishing the rectangle with some light sanding. Note that a hole was drilled and threaded in the center so that a screw could be inserted for the purpose of holding the turntable for turning on the lathe, and then this hole went away when the rectangle was cut.
- From 1/4" thick maple plywood, cut three rectangles to be significantly larger than the puzzle will be (e.g., 1" bigger on all sides); save rectangle 1 for the bottom of the puzzle. Cut rectangle 2 to be an L-shape for the left and top sides of the puzzle, but leaving it too thick and two long in both directions. Cut a hole in Rectangle 3 for the turntable and then cut it to be an oversize L with a partial circle positioned in the corner.
- Trim off the ends of rectangle 1 a little bit at a time until you get a nice fit for the pieces to move around when it is pushed together with rectangle 2 (use a miter saw to make clean ends so that the two seams will no show much).
- Using white glue, glue the L's onto the bottom piece, and let dry.
- Trim the puzzle to be square but still oversized with a band saw, and then using a table saw, trim to leave a 1/2" border around the puzzle area.
- From a dark wood cut 4 sticks that are 1/2" wide, 3/8" thick, and longer than the edges of the puzzle. Glue them to the edges of the puzzle in an overlapping pattern going around, leaving the excess ends sticking out:

- After the sticks have dried, trim off the excess with a band saw. Then, on a table saw, make final passes on the edges to form a uniform 1/4" wide dark wood border.
- Print on light cardboard stock a cover to slide over the puzzle, cut and fold to fit the puzzle so that the ends overlay about 3/4" on the back side, and use a glue stick to join the ends (for a bigger puzzle join in two places to a second piece on the back).

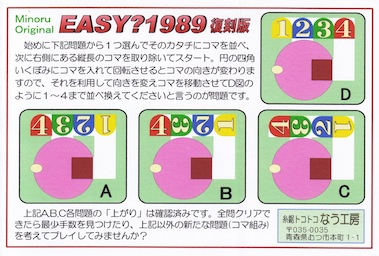

Designed by Minoru Abe circa 1989; this one purchased 2013.
(cardboard box and wood puzzle, 4.25" x 4.25" x 7/8")
The directions show 9 problems named A - C and 1 - 6 to remove the 2x1 keeper and rearrange the pieces to read 1 2 3 4 oriented properly, starting and ending with the blank piece in the turntable in its east position. Any permutation / orientation can be achieved by a combination of cycling positions (1,3), (1,4), (2,4), (3,4) while parking a piece in position (1,1), and exchanging pieces located in positions (1,1) and (1,3) by using the turntable slot in its north position, but finding a shortest sequence is harder. We consider three rules for counting moves:Rule 1: A single move may pass through the turntable independent of initial orientation.Although not the hardest, Problem 3 is arguably the most asthenic, and shown on the right above are 3 additional problems along those lines. Here are the rectilinear moves for solutions using each of Rules 1, 2, and 3 for the total of 12 problems:
Rule 2: A single separate move is required to use the turntable.
Rule 3: Repositioning the turntable requires an additional move. For example, moving horizontally, then rotating, then moving vertically, is 3 rectilinear moves if the turntable is east before the move, or 4 rectilinear moves if it must first be rotated.
Problem A
40, 56, 67Problem B
46, 64, 76Problem C
58, 78, 92Problem 1
42, 56, 67Problem 2
52, 71, 84Problem 3
26, 37, 46Problem 4
60, 83, 99Problem 5
57, 75, 88Problem 6
53, 71, 83Problem 7
32, 40, 48Problem 8
38, 55, 68Problem 9
22, 30, 35
Here a 26 rectilinear moves solution using Rule 1. Solving using Rules 2 or 3 can work the same by inserting extra moves at the appropriate places to achieve 37 or 46 rectilinear moves:

Designed and made by J. A. Storer, 2024.
(3D print, PLA plastic, 80mm x 164mm x15mm)
Remove the four circle keepers and starting with 54321, slide the pieces to be 12345; relatively easy, but fun. The two ends of the red "shuttle" are connected by rods in tracks under the 1,2,3,4,5 pieces (puzzle back is blank except for copyright):

For rectilinear moves where one move is defined as moving one piece (without pushing others), then the puzzle can be solved in 38 rectilinear moves. But if a piece can push one or more other pieces, then as shown below 22 push moves suffice.
For example, for move 2, piece 2 slides right and down while pushing 1,3,4,X (where X denotes the red slider), and for move 14, piece 1 moves left and down pushing 2,3,X.


Designed and made by J. A. Storer, 2024.
(3D print, PLA plastic, 80mm x 164mm x15mm)
Remove the four circle keepers and starting with 4321, slide the pieces to be 1234. Construction is similar to Shuttle Five (except copyright on top, not on the back). Arguably too easy for an adult, but perhaps appropriate for a child. Can be solved in 10 push moves:


Designed and made by J. A. Storer, 2024.
(3D print, PLA plastic, 80mm x 164mm x15mm)
Remove the four circle keepers, and starting with 321, slide the pieces to be 123. Construction is similar to Shutle 1234 (except copyright on the back), but even easier for a young child. Can be solved in 7 push moves:


a.k.a. Sliding Eight II
Made by Minory Abe, circa 1985.
(wood 2+13/16" x 7+7/16" x 7/8" with 10 pieces and a keeper piece;
tray itself is 5/8" high, numbers are 3/4" square by 9/16" thick; sleeve made by J.A. Storer)
Two long pieces can slide left or right to shift the numbers contained in each of their four slots. A number can move from the slot of one to an empty slot of the other or from the leftmost or rightmost slot of one to after the right or left of the other. The problem is to reverse the numbers:
The following page outlines a solution of 124 moves.
Call the upper long piece X and the lower one Y. Solving may move 4 out of the left slot of X to the left of Y so that Y is "locked" from moving and the leftmost slot of X is empty at Step 4:

Next a "X round" alternates a move of X and with the only legal move of a number between a slot of X and Y until the rightmost slot of X is empty at Step 15:
Next, after moving 1 and 4 up, X is locked, and a "Y round" alternates a move of Y with the only legal move of a number between a slot of X and Y until the leftmost slot of Y empty at Step 30:
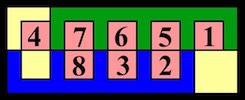
Next, move 4 down, X left, Y right, and 2 up, so X is again locked and now a Y round leaves the leftmost slot of Y empty, and 7 and 2 move down to leave the leftmost slot of X empty at Step 49:
Continue with an X round to step 64, another X round to step 74, some small X and Y rounds to Step 83, a Y round to Step 92, some manipulations to Step 96, a Y round to step 107, two moves to start new X round at step 109, a X round to Step 120, and moves to finish at Step 124:
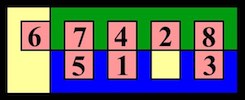
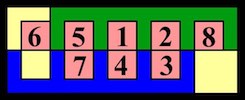
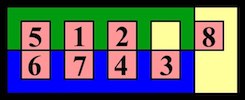
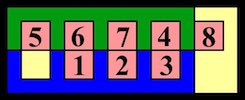


Designed and mad by Minoru Abe, circa 1985.
(cardboard box 5+1/4" x 6.25" x 7/8", 10 wood pieces, blue keeper, and directions)
The directions show three positions, giving rise to three problems:
The following three pages show solution for the three Shimokita problems.
Similar to the Moota-Kun puzzle by the same designer, a tricky solution to start with is made more difficult because it is cumbersome at first to keep track of where pieces need to go when they are portions of a drawing rather than plain colors.
The big piece at the bottom has a nook that makes it natural to perform a capture movement where it slides left or right with another piece in its nook. Here, we limit capture movement to one of the small pieces being carried, where when in the nook the small piece does not extend beyond the bounding rectangle of the big piece.
The following three pages show solutions for the three Shimokita problems where capture movement is allowed. Note, however, that by using move moves, without any capture movement Shimokita 1 -> 3 can be solved in 58 rectilinear moves, Shimokita 1 -> 2 in 55 rectilinear moves, and Shimokita 2 -> 3 in 65 rectilinear moves.
The figures here have piece labels added to match the solutions on the following pages. In all three solutions, the big piece labeled X, stays on the bottom and moves only two times.
For the main 1 -> 3 problem, here are positions 13 and 39 just after each move of X:


For the 1 -> 2 problem, here are positions 23 and 37 just after each move of X:


For the 2 -> 3 problem, here are positions 20 and 46 just after each move of X:

Here is a solution of 51 rectilinear moves (72 straight-line moves):

Here is a solution of 50 rectilinear moves (69 straight-line moves):

Here is a solution of 58 rectilinear moves (81 straight-line moves):


Designed and made by Diniar Namdarian, 2016; sleeve by J. A. Storer.
(plastic, 5+1/8" high by 5+1/8" wide x 3/8" thick; H arms are 1/3 the width of a square)
The H piece can slide carrying one or two pieces with it. Starting with red 1-2-3 on the left and orange 1-2-3 on the right, "Problem 1" is exchange them:
One can place a finger on the H itself or on one of the pieces it contains to push, which can move two pieces with the H, or only one, where another may be left behind. The directions show 9 other problems, all with the same end position as the start position for Problem 1:
The next page shows a solution of 57 moves for Problem 1; moves to solve the others are:2 = 35 moves, 3 = 49 moves, 4 = 31 moves, 5 = 54 moves, 6 = 40 moves,
7 = 36 moves, 8 = 46 moves, 9 = 29 moves, 10 = 47 moves,
Here is a solution of 57 rectilinear moves (60 straight-line moves):


Designed and made by Diniar Namdarian, 2016; sleeve made by J. A. Storer.
(laser cut plastic, 7+1/8" high by 5+1/8" wide x 1/2" thick)
Referring to the figure on the right above, on the left and right are 4 rectangular pieces where in the left the background color is a light blue and on the right it is a darker blue. Both sides have raised red plastic showing 4 size cups, labeled here as 1 to 4 on the left and A to D on the right. In the center is a single piece, labeled here as S, that has two sections connected by strip under the pieces. The S piece forms a slider that can go up and down and carry / push pieces with it.
The puzzle name comes from the classic Towers of Hanoi problem, here the basic problem is:Problem 5": Exchange the two towers.The puzzle directions also give four other problems:1: Invert the left tower.The following pages show solutions where all moves are simple straight-line movement:
2: Exchange 2 and B, exchange 4 and D.
3: Invert both towers, exchange 1 and A, exchange 3 and C.
4: Invert both towers.Problem 1: 99 moves
Problem 2: 95 moves
Problem 3: 93 moves
Problem 4: 106 moves
Problem 5: 64 moves
In all of the solutions presented, a single slide of the S piece counts as one move, which may have the effect of repositioning the one or two pieces between the two portions of the S piece.
If there are two pieces on the slider, then a single finger can push the slider, and they move as the slider moves. However, if there is only one piece on the slider, then exactly what happens depends on the puzzle construction.
Consider the S move depicted in the figure below. If the connection between the two parts of the slider does not contact the underside of the pieces on the slider (it goes under the puzzle or is a strip recessed down a bit and not as wide as a piece) then a single finger can push the S piece down where it bumps into piece 4 and finishes the slide with piece 4 in the correct position.
However, this puzzle is constructed with a strip connecting the two halves of the S piece that is as wide as a piece and level with the bottom of the pieces (and contacts the bottom of pieces on the strip), and so piece 4 moves with S as soon as it is pushed, and has to be stopped with a finger when it is in position, or it will be dragged too far down and then a second move has to push it back up.If one wants to count these situations as two moves, then the move counts for the solutions presented here can be adjusted upward accordingly.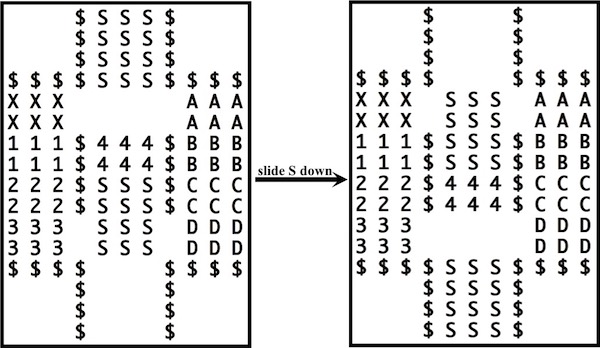
Here are moves 11, 22, 33, 44, 55, 66, 77, 88, 99 of a 99 rectilinear moves solution:

Here are moves 11, 22, 33, 44, 55, 66, 77, 88, 95 of a 95 rectilinear moves solution:

Here are moves 10, 20, 30, 40, 50, 60, 70, 80, 93 of a 93 rectilinear moves solution:

Here are moves 12, 24, 36, 48, 60, 72, 84, 96, 106 of a 106 rectilinear moves solution:

Here are moves 7, 14, 21, 28, 35, 42, 49, 56, 64 of a 64 rectilinear moves solution:


Designed by the Garbarchuk family; made by Diniar Namdarian 2012, sleeve by J. A. Storer.
(laser cut plastic 3.2" x 5.5" x 3/4", tray and 8 pieces)
A large piece containing two U-pieces, each covering half a disc, with along the bottom two curved pieces at the left and right and a square in the middle. The discs and bottom three pieces are all 2 units high and wide, the U-pieces are 2 units high by 4 units wide, the big piece is 4 units high by 10 units wide, and the tray interior is 6 units high by 12 units wide.
The puzzle directions, show three problems: Part 1 is to exchange the discs, Part 2 is to exchange the two U-pieces, and we refer to Part 3 as going from Part 1 start directly to Part 2 end.
The following pages report solutions for three ways to count moves:Generalized Rectilinear Moves: One move is pushing a single piece with one finger, where that piece may push or drag other pieces with it. A second finger may NOT be used to aid movement, prevent a piece from being dragged to far, etc.It is worth noting, that Part 2 can be easily solved by employing a combination of rotating and sliding. Slide the discs down, slide the big piece to the right, slide all the other pieces except the two U-pieces to the left and up, and now manipulate the two U-pieces and the right most bottom piece; here are three key positions:
Rectilinear Moves: Generalized rectilinear moves where, except for a group contained by X, a piece may not push other pieces.
Restricted Rectilinear Moves: Rectiliner moves with the restriction that for a group contained by X, the finger must be placed on X and not any of the pieces it contains (further adjustment of a piece inside X after the move of X is an additional move).

Here is a 31 generalized rectilinear moves, where one move is pushing a single piece with one finger (where that piece may push or drag other pieces with it).
If pieces (except for X) are not allowed to push other pieces, move 7 can be replaced by 2 moves and move 26 by three moves for a solution of 34 rectilinear moves. In additon, move 17 can be replaced by two moves for a solution of 35 restricted rectilinear moves.
Here is a 43 generalized rectilinear moves, where one move is pushing a single piece with one finger (where that piece may push or drag other pieces with it).
If pieces (except for X) are not allowed to push other pieces, moves 11, 16, 21, 24, 28, 33 can each be replaced by 2 moves for a solution of 49 rectilinear moves. In additon, moves 14, 30 can each be replaced by two moves for a solution of 51 restricted rectilinear moves.
(continued on next page)
Here is a 51 generalized rectilinear moves, where one move is pushing a single piece with one finger (where that piece may push or drag other pieces with it).
If pieces (except for X) are not allowed to push other pieces, moves 11, 16, 21, 23, 28, 41 can each be replaced by 2 moves for a solution of 57 rectilinear moves. In additon, moves 14, 25, 38 can each be replaced by two moves for a solution of 60 restricted rectilinear moves.
(continued on next page)
Adapted from the Sliding Three puzzle, J. A. Storer, 2020.
(Planned construction for 3d print, 2.7" x 4.7" x 3/8" thick, with cardboard sleeve.)
A variation of the Sliding Three puzzle puzzle where all interior and exterior rounds have been eliminated, except for the two discs.
The start is a large piece containing Square U-shaped pieces, each covering half a disc, with along the bottom three square pieces. The discs and squares are all 2 units high and wide, the U-pieces are 2 units high by 4 units wide, the big piece is 4 units high by 10 units wide, and the tray interior is 6 units high by 12 units wide.Problem 1: Exchange the discs. A solution that is identical to a Part 1 solution for the Sliding Three puzzle of 34 rectilinear moves (43 straight-line moves) is shown on the following page.All three solutions have some steps that involve moving the big piece while containing other pieces, and can be performed by pushing with a single finger on one of the pieces.
Problem 2: Exchange the Square U-pieces. A 40 rectilinear moves (54 straight-line moves) solution is shown on the following pages.
Problem 3: The combination of Problems 1 and 2 to exchange both the U-pieces and the discs. It can be done in Square steps by first solving Problem 1 and then Problem 2; the following pages show a shorter combined solution of 52 rectilinear moves (66 straight-line moves).

Designed by Minoru Abe, Made in Japan 2013.
(cardboard box 5" x 4.3" x 7/8", wood tray, 9 wood pieces and wood keeper)
The directions give 4 problems that have rectilinear solutions of 61, 47, 47, 49, moves respectively. Here are the first, every 6th, and last position of a 61 rectilinear (69 straight-line) moves solution to problem 1:

Designed by Minoru Abe, this one made by J. A. Storer 2011.
(cardboard sleeve, Purple Heart, Cherry, Maple tray and pieces, 4.6" x 8" x 5/8")
The start position has pieces labeled 1, 2, 3, 4 (in that order) along the bottom, and on top a U-shaped piece X that has piece O captured inside. The goal is to slide the pieces so that 1, 2, 3, 4 (in that order) is on top. One way to think of solving is to repeatedly place the puzzle in a position where there is an empty vertical column that allows pieces to be exchanged. Here are the start position, the end position, and each of the empty column positions in a 45 move solution (and with 1 or 2 additional moves the X and O pieces can be arranged as desired on the bottom).

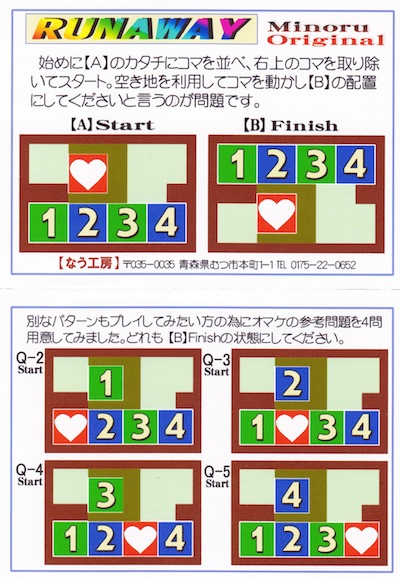
Purchased 2012.
(wood tray and pieces in a cardboard box, 3.7" x 5" x 7/8")
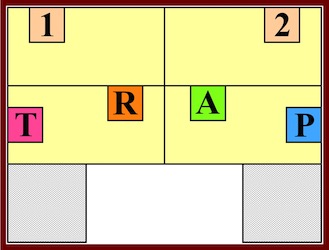


>

A modification of the Trap puzzle by Minoru Abe, by J. A. Storer, 2020.
(3D print design by J. A. Storer 2024 on a Bambu A1 Mini with 4-color AMS;
118 x 140 x 16 mm cover that slides over the puzzle has directions glued to the underside)
At first glance this puzzle looks identical to the Trap puzzle by Minoru Abe, but there is a small difference in construction that makes a significant difference to solving. The problem is the same, to exchange 1 with 2 and TRAP with PART:
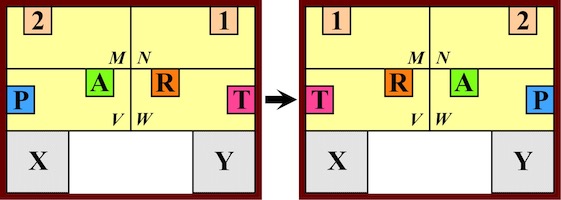
However, for Trap the size of the little squares 1, 2, T, R, A, P is more than half the height of the big pieces, and as a consequence cannot pass each other in a region of big piece height. For Easy Trap, the height of the little squares is less than half that of the big pieces. A same approach to solving as for Trap can be used - determine all of the positions that allow the swap of two letters, and then minimize the number of swaps. Although any solution for Trap may be used, such as the Hordern solution that uses 9 swaps, Easy Trap can be solved using only 5 swaps:

Here is a solution of 60 rectilinear moves (continued on the next page):

Designed by Minoru Abe 1986, this one made by J. A. Storer 2008.
(cardboard sleeve, cherry tray 4" x 5" x 5/8", 12 metal 1/4" thick pieces
with plexi-glass keeper; left half is aluminum and right half is brass)
There are four 1x2 rectangles, two 1x1 squares, and six 5/8x5/8 little squares labeled 1, 2, P, A, R, T; The rectangles have receptacles into which a little square can fit. Each little square is larger than 1/2 unit on a side, so that two little squares cannot pass each other in 1 unit wide opening (see Easy Trap where they can, and a shorter solution is possible, which for some may be more fun). The goal is to start with it reading 2 1 P A R T and slide the pieces to make it read 1 2 T R A P, where rectangles end up in the same positions as they started (piece coloring is just decorative).

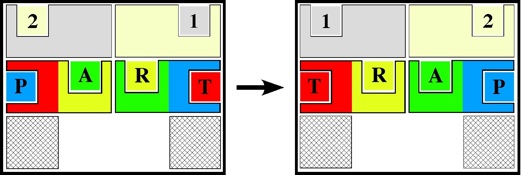
Hordern's book gives a solution of 177 rectilinear moves (196 straight-line moves), where a rectangle moving with little squares in its recepticle(s) counts as one move. Baxter's Minoru Abe Gallery indicates a solution of 174 rectilinear moves (which he has credited to Jim Henderson), which can be achieved by a slight modification to Hordern's solution. Those who enjoy this puzzle should also try the Tricky puzzle.
Further Reading
Baxter's Abe Gallery, from: http://www.johnrausch.com/SlidingBlockPuzzles/gallery.htm

Purchased 2012.
(wood tray and pieces in cardboard box, 5.4" x 6.375" x 7/8")
Hordern first determines the positions that allow one to exchange a pair of little squares, and finds that there are six possible exchanges that can be performed (there are six positions each for performing the 1<->P and 2<->T exchanges, whereas the other four each have a unique position in which they can be performed):
Solving amounts to planning a sequence of exchanges. Hordern finds that nine exchanges are needed, and gives a basic argument that 7 exchanges suffice to get A and R to their correct positions, where some ways of doing this need only two additional exchanges to fully solve the puzzle. He then finds that it takes between 7 and 27 moves to go between any one exchange position and another, notes that there are several orderings for nine exchanges that use a total of 179 moves, and presents this 177 move solution:
Partial Capture Moves: A little square can move (when there is room to move) by placing a finger on it and sliding it. This is also true of rectangle. However, if it is desired that a rectangle move so as to carry along with it the little square(s) it contains, it may be necessary to place a finger on a little square so that pushing it also results in pushing the entire assembly without a little square being left behind. Allowing such partial capture moves can save a move.
Below are the start and end positions and each of the nine positions that Hordern's solution visits to exchange a pair of little squares. The larger pieces are labeled M, N, V, W, X, Y.
We use a more verbose notation than Hordern's book. The first letter is the piece to be moved and the second letter is the direction; all moves are a distance of 1 unit unless followed by a 2 (to specify two units). Two consecutive moves of the same piece are listed together as a single rectilinear move. The little squares are denoted 1, 2, T, R, A, P, the two top rectangles by M and N, the two middle rectangles by V and W, and the two bottom large squares by X and Y.
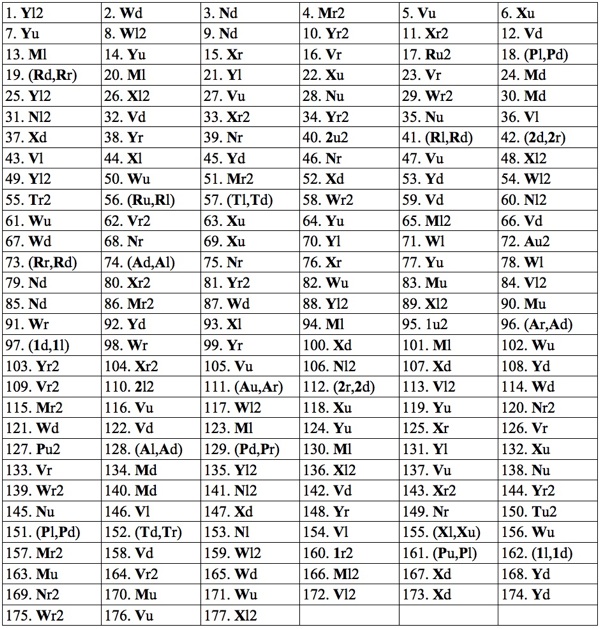
(177 rectilinear moves, 196 straight-line moves)
A two move reduction can be achieved by changing what happens at position 54 to accomplish the effect of the four moves 55 through 58 in three moves (left below) and also at (now) position 108 to accomplish the effect of the four moves 109 through 112 in three moves (right below):
An additional move can be saved by using a partial capture move for exchange 9. As shown here, partial capture moves can also be used for exchanges 3 and 6 (but are not necessary for those exchanges, which can instead be done in the same number of moves by employing a capture move that slides over a small square). Below are the start, end, and each of the nine positions where an exchange occurs.
For a 174 rectilinear moves solution, we again use a more verbose notation than Hordern's book. The first letter is the piece to be moved and the second the direction; all moves are a distance 1 unless followed by 2 (moves of a little square by a non-integral distance less than 2 count 1 unit). Two consecutive moves of the same piece are listed together as a single rectilinear move. The little squares are denoted 1, 2, T, R, A, P, the two top rectangles by M and N, the two middle rectangles by V and W, and the two bottom large squares by X and Y. In addition / means do not move that letter; e.g., Wl2/T means move W left two units but without dragging the T with it.
(174 rectilinear moves, 193 straight-line moves)
Define a partial capture move as one where the capture piece slides away from a captured piece and leaves it behind, and a catch capture move as one where the capture piece slides over a piece at the end of its move to capture that piece.
Computer simulation of Hordern's solution computed a solution of 175 rectilinear moves that uses only catch capture moves for exchanges and no partial capture moves. That solution can be reduced by one move to 174 rectilinear moves by using a partial capture move for the final exchange.
In the output shown below for exchange 9 of the 175 move solution, move 157 can use a partial capture move to leave piece 1 behind, and move 158 can be eliminated (position 159 now has piece 1 at the middle right, and move 60 can move piece 1 into piece M):

Designed by Minoru Abe 2008,



left made by J. A. Storer 2009, right purchased in Japan 2010.
(left: Cherry tray with 1/2 inch thick Walnut and aluminum pieces, 4.5" x 7.5" x 1",
right: wood tray, 7 wood pieces, and a wood keeper, 3.3" x 4.7" x 3/4")
A smaller puzzle in the theme of Trap, where here both exchanges and transfers are possible. The Abe puzzle instructions present five problems for arranging the numbers so they read 1-2-3-4 from left to right, the first of which is starting with them in the order 4-3-2-1 as shown on the right above (the other four are to start with 1-3-2-4, 2-3-4-1, 3-1-2-4, or 4-1-3-2). All five problems require that the blocks end up in their original positions (next page). It is a good warm up exercise to first ignore this requirement and solve the easier problem to read 1-2-3-4 on the bottom; starting with the position on the right above, here is a way to do that in 16 moves, using only transfer operations:
Call operations that move discs when the blocks are positioned in three of the four quadrants as "standard operations". Here is a map of the possible standard operations, where a line goes between two places if a transfer can be made and a line has double arrows if an exchange is also possible, where an s next to the line indicates that the exchange is possible for the version made by J. A. Storer shown on the previous page (the "disc version") but not in the Abe version (which instead of discs has little squares of a slightly larger relative size):

Rearranging to 1-2-3-4 is not possible using only the standard operations (there is no way to get 3 out of the way to clear a path for 2). Key are trick operations where, when positions C and Y are empty, an upper and lower disc can exchange places by circulating around a block:
Left Trick
Right Trick
Here are basic solution steps (red, blue, and green denote a move of the blocks that start in the upper left, upper right, and lower left respectively):1. blue, 2 -> Y (transfer - 1 move)The following two pages show how to implement a left trick with 5 moves, a partial left trick with 7 moves, and a right trick with 8 moves, for a total of 60 moves (or 56 moves for the disc version if the two left tricks are replaced with a standard exchange of 3 moves).
2. red, 4 -> X (transfer - 1 move)
3. green, 2 -> A (transfer - 1 move)
4. green, 2 <=> 4 (left trick - 5 moves)
5. red, blue, green, red, blue, 2 <-> 1 (standard exchange - 3 moves)
6. blue, red, green, blue, 2 <=> 3 (right trick - 8 moves)
7. red, 1 <=> 4 (left trick - 5 moves)
8. red, blue, green, red, blue, 3 <-> 4 (standard exchange - 3 moves)
9. blue, red, green, blue, red, 3 => C (partial left trick - 7 moves)
10. red, blue
A sequence of 11 rectilinear moves can be used for a left and right trick in an approximately symmetric fashion; they are the same for the Abe and disc versions, except that for the disc version the central block (green for a left trick or blue for a right trick) is vertically centered at step 2, whereas in the Abe version, it is all the way in and shifted down as much as possible):N. Baxter has observed that the number of moves for both tricks can be reduced. The left trick is 5 moves by not circulating disc L and employing a move that drags the green block by pushing disc U, and the right trick is 8 moves by a highly non-rectilinear move of the blue block that detaches from disc L and captures disc U:
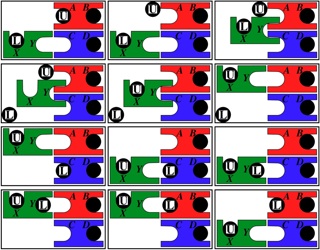
Left Trick
Right TrickAlthough a left trick is possible in the disc version, it is not needed because a standard exchange between positions A and X can be used instead. This additional exchange reduces the number of moves in a solution but does not make achieving 1-2-3-4 significantly easier (since once the right trick is discovered, so will the left trick); in fact, it may make the puzzle a bit harder because initially one may be more likely to think a solution with standard moves is possible.
Left Trick:
1. U comes out of the red block.
2. Green goes to the trick position.
3. L goes up to the upper left corner.
4. U goes into the green block
and pushes it to the lower left.
5. L goes into the red block.Right Trick:
1. Disc U goes straight to the right.
2. Blue block moves away from disc L,
captures disc U, and ends in the upper right.
3. Disc L goes into the green block.
4. Blue block moves down.
5. Disc L moves into the blue block.
6. Blue block moves up.
7. Disc L moves into the red block.
8. Blue block moves down.
Returning to the straightforward 11 steps for a left trick, observe that after move 7, disc L is in position C, and with one more move disc U can return to A for the net effect of moving disc L from X to C in 8 moves; we can optimize this to work in 7 moves:1. Disc 1 comes out.
2. Green block goes to the trick position.
3. Disc 3 moves to the lower left corner.
4. Disc 1 goes into the green block.
5. Green block goes to the upper left.
6. Disc three goes into the blue block.
7. Disc 1 pushes the green block down and then moves into the red block.
Note: The very next move after the partial left trick is to move the red left, so another way to implement step 7 of the partial left trick in this situation is: in move 5 of the partial left trick, do not move the green block all the way up, so now move 7 can move the green block down, leaving disc 1 behind, to be captured by the red block.
Here is the start position and the position after each of the basic steps:
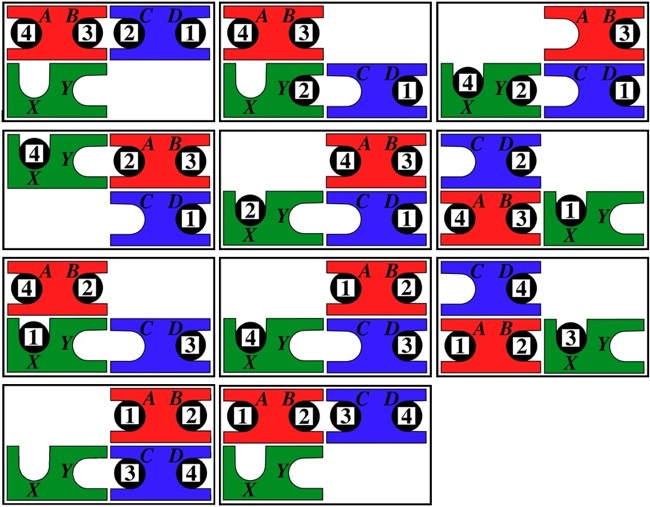
A shorter solution, that works for both the Abe and disc versions, can be achieved by using a different sequence (transfer, transfer, left trick, right trick, exchange, right trick, left trick, transfer) and optimizing local movements. Here are selected positions of this 49 rectilinear (69 straight-line) moves solution; it allows the capability for a piece to leave a captured piece behind during a move, and also to catch one during a move and continue on with it (if this capability is forbidden, then moves 3 and 48 can each be replaced by two moves, for a 51 moves solution).

For the disc version, the solution of the previous page is 46 moves (61 straight-line moves) by saving a move in the sequence at step 14 and saving two more moves in the sequence at step 39. For example, at Step 14, the disc version's ability to directly exchange discs at position A and X, allows us to keep disc 1 with the green block because there will be enough clearance to move it up past disc 2 into the red block.

Here is an equivalent 46 moves solution to that for the disc version on the preceding page; it uses squares of a size smaller than the Abe version (to allow the same clearences as for the discs):


Designed by Minoru Abe, produced in Japan circa 1990.
(cardboard box, wood tray, 8 wood pieces, and wood keeper, 5 by 5.25 by 1 inch)
There are four 1 unit square pieces, three 2/3 units high by 1 unit wide pieces, and a large U shaped piece that is 1+23 units high on left and 1+1/3 units high on right, with a step down to a 2 unit wide space and a second step down in the middle to a 1 unit wide space. The directions that are shown on the puzzle box top are to remove the big keeper piece and switch the dog and cat:

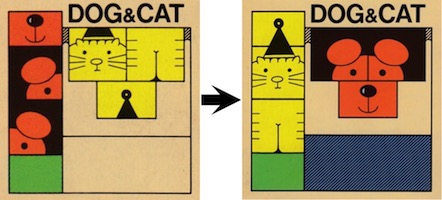
Besides moving the big piece down at the start and back up at the end, the big piece only moves left once and then back right once in the 67 rectilinear moves solution shown on the following two pages. However, given that it is a tricky solution, and it can be useful to start with the easier problem of solving the puzzle without the small blank piece, which can be solved in 51 rectilinear moves (or 47 rectilinear moves if started with the cat assembly at the bottom).

Designed and made by Diniar Namdarian, 2016; sleeve made by J. A. Storer.
(laser cut plastic, 4.75" high by 5.5" wide x 3/8" thick)
The problem is to move the dog to the middle of the four squares:
The next page shows a solution of 52 rectilinear moves.
Here is every 4th move of a 52 rectilinear moves (61 straight-line moves) solution:


Designed and made by D. Namdarian 2013; sleeve added by J. Storer.
(made from 1/8" thick laser cut plastic, board 2 layers, pieces 2 layers, 4.375" x 4" x 3/8";
the eight pieces are two layers only due to the dog ears)
The start position has the two dogs facing away from each other and the other 6 pieces neatly arranged above them. A natural problem is to exchange the two dogs while leaving the rest of the puzzle the same. A second problem, shown in the puzzle directions and sample solution, is where one of the square pieces ends up above the dogs and one between them.
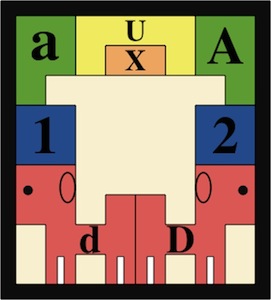
StartPosition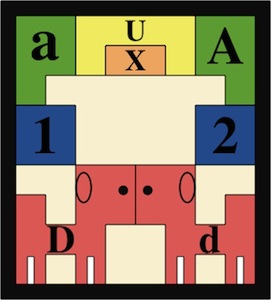
Problem 1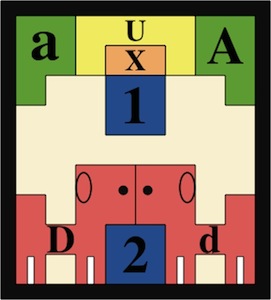
Problem 2
The directions allow pieces that are touching to move together; we call this a join move. Also, we say that a join move is an interlocked move if it is not possible to replace it by moving its pieces one at a time. For this puzzle, join moves are not merely a way to count moves; the puzzle cannot be solved without employing some interlocked moves.
The next page show a 27 move solution to Problem 1. In Step 14, X drags U and then lets it go before the end of the move; it this is considered illegal, then Step 14 can be replaced by two steps for a solution of 28 moves. If movement is restricted to only allow join moves that are interlocked, then steps 3, 4, 6, 11, 14, 16 can each be replaced by two moves (one of them possibly interlocked) for a solution of 33 moves.
Following the solution for Problem 1 is a 24 move solution to Problem 2. Like Problem 1, if Step 14 is considered illegal, replace it by two moves for a solution of 25 moves. If movement is restricted to only allow join moves that are interlocked, then steps 3, 4, 6, 8, 14, 20, 21 can each be replaced by two moves (one of them possibly interlocked) for a solution of 31 moves.

Designed and made by D. Namdarian 2014; sleeve added by J. Storer.
(made from 1/8" thick laser cut plastic, board 2 layers, pieces 1 layer, 3.6" x 6.75" x 1/4")
The puzzle directions show these two problems:
The puzzle sample solutions for Problem 1 and Problem 2 show that movement may be a collection of pieces that touch each other moving together. The following two pages show solutions for the two problems with the following rule for moves:Generalized Rectilinear Moves: One move is pushing a single piece with one finger, where that piece may push or drag other pieces with it. A second finger may NOT be used to aid movement, prevent a piece from being dragged to far, etc.--- 1303 --- Stacking Cups Solution, Problem 1Here is a 31 generalized rectilinear moves solution, where one move is pushing a single piece with one finger (where that piece may push or drag other pieces with it). For each position, the piece that was moved is changed to black.

--- 1304 --- Stacking Cups Solution, Problem 2Here is a 35 generalized rectilinear moves solution, where one move is pushing a single piece with one finger (where that piece may push or drag other pieces with it). For each position, the piece that was moved is changed to black.


Designed and made by D. Namdarian 2014; sleeve added by J. Storer.
(made from 1/8" thick laser cut plastic, board 2 layers, pieces 1 layer, 3.6" x 5.6" x 1/4")
A puzzle with many pieces and much white space. The solution sheet that comes with the puzzle shows a 105 basic steps, many of which are composed of several rectilinear moves where some require two pieces to slide together; here a 12 of those positions:



Designed and made with a 3D printer by Diniar Namdarian, 2018; sleeve added by J. Storer.
(plastic box 4.1 x 5.2 x 1/2 inches, 10 plastic pieces, and directions with solution pdfs)
The problem is to exchange the eyes. The circles slide on top of the pieces, where each have a raised portion, named "eyebrows" by the puzzle directions, that each can pass over everything except the opposite eyebrow. The precision afforded by this nice example of 3D printing provides for smooth sliding of the pieces.
In addition to allowing curved pieces, the solution that comes with the puzzle allows a piece (or a number of interlocking pieces) to push another piece (or a collection of interlocking pieces) as it moves; we refer to this as generalized rectilinear movement. For example, steps 16, 19, 25. 39, 49 of this solution move two pieces at once. Although this solution is presented as 65 generalized rectilinear moves, it appears that it can be improved to 59 generalized rectilinear moves, by combining steps 21+23, 26+27, 33+34, 44+45, 50+51, and 62+63.
At first, the puzzle looks to have a relatively simple solution that that exchanges an eye with the mouth, then exchanges the two eyes, and then exchanges the other eye with the mouth. Without the eyebrows this idea works, and a solution of 41 rectilinear moves (37 generalized rectilinear moves) is shown on the following three pages.
However, with the eyebrows, solving is more complicated. Following the three pages of the solution without eyebrows, is a 68 rectilinear moves (61 generalized rectilinear moves) solution.
Shorter solutions are possible by allowing the circles to be half on a piece and half hanging over empty space, but such movement is not allowed by the puzzle directions, and is not natural.
Note: For a solution of 37 generalized rectilinear moves (where pieces can be pushed by others), combine 3+4 (1 pushes 3+4+C east and continues north), 12+ 13 (2 pushes M north and continues east), 24+25 (1 pushes M north and continues west), 36+37 (2 pushes M north and continues east).
Note: For a solution of 61 generalized rectilinear moves (where pieces can be pushed by others), combine 12+13 (1 pushes 4 south), 21+22 (2 pushes 4 east and continues north), 30+31 (3 pushes M+1+A east and continues south), 48+49 (2+4+C pushes 3 east), 52+53 (2+4+C pushes M north), 58+59 (3 pushes 2 north), 61+62 (2 pushes 3+4+C south and continues east).


Siebenstein - Spiele 2011, Germany.
(wood and plastic, 3.7" x 3.7" x 5/8")
The puzzle works by using your fingers through the four large square holes in the plastic top. The top is nice for storage and transportation, but makes it hard to manipulate pieces; it can easily be temporarily removed for play by undoing the four corner screws (loosened with a screwdriver in the slots on the back side). Pieces can be rotated from certain positions. For example, from photo 1, the middle piece alone can be rotated counterclockwise (photo 3) or both can (photo 4):







Problem 1: Put the female symbols together and leave the other pieces neatly at the bottom:Problem 2: Put the female symbols together and leave the other pieces in the positions as shown on the directions, in their original orientations: Problem 3: Put the female symbols together and leave the other pieces in the positions and orientations as shown on the directions:
Problem 3: Put the female symbols together and leave the other pieces in the positions and orientations as shown on the directions: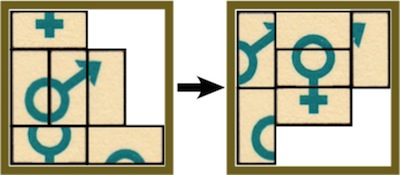
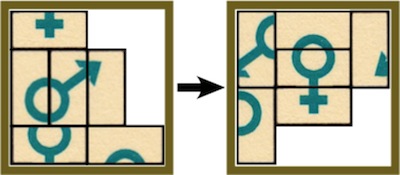
For solutions to be presented we charge for rotations as follows:
Type 1: Any of the 4 variations where block 1 on the left could be positioned 2 units to the left or block 1 on the right could be positioned 2 units down, count as 1 move:Type 2: Counts as 2 moves: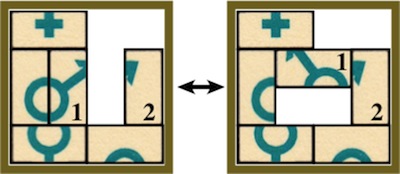 Type 3: Counts as 1 move:
Type 3: Counts as 1 move: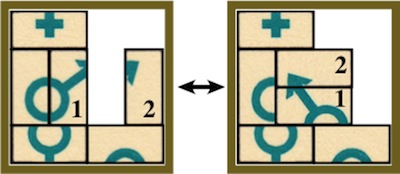
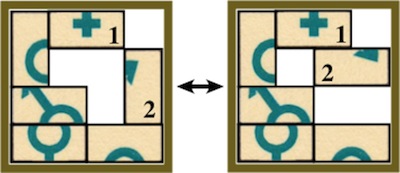
Here is a 23 rectilinear (29 straight-line) moves solution that uses only one rotation (a type 1 rotation at step 2):
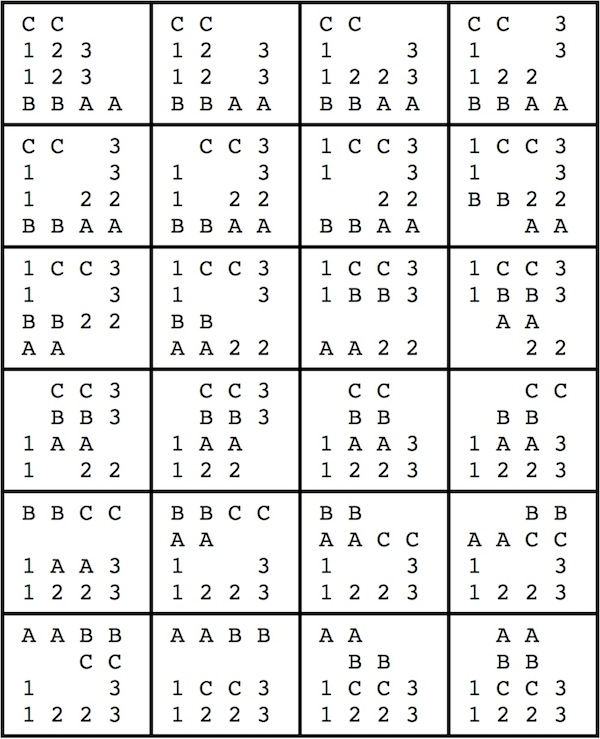
Here is a 31 rectilinear (39 straight-line) moves solution that uses only two rotations (a type 1 rotation at step 2 and step 21):
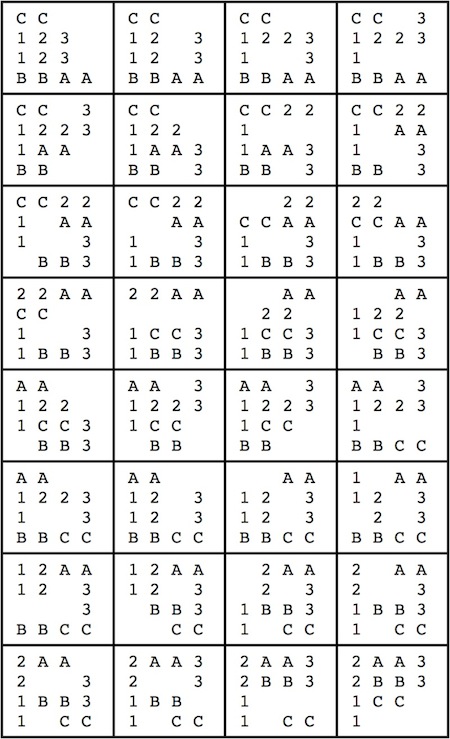
Here is a 55 rectilinear (62 straight-line) moves solution that uses 5 rotations; Type 1 at step 47, Type 2 at steps 2&3 (the two steps represent the cost of 2 for this double rotation), and Type 3 at steps 11, 20, 43). This solution does not allow rotation steps to be combine with other steps; otherwise, by combining the double rotation steps 2&3 with step 4, and combining the rotation step 47 with step 48, this solution translates to 53 rectilinear moves.

Maple, Walnut, Yellowheart, Paduak, Bubinga, Acrylic, 3.75 x 3/4 inches
(Maple, Walnut, Yellowheart, Paduak, Bubinga, Acrylic, 3.75 x 3/4 inches)
Take out the center piece and then work around to progressively manipulate / rotate the pieces until one can be removed. Hard to use; a wet fingertip or sticky finger may be needed to pull on the edges of the pieces. Here is what the puzzle maker said:"Another one by Goh Put Khiam, Fusion is the successor of RetroFit. As you would expect from how tricky RetroFit was, Fusion takes it to another level. The goal, to fit the five polyominoes into the partially covered tray, is MUCH trickier than it looks. Here is what Goh has to say about it: This is a redesign of my Crossroad puzzle. In that puzzle, the pieces are complex and the cover of the box requires eight protruding tabs. This has been greatly simplified in this design which I called Fusion because the "round" piece is suspended in the centre much like what happens in a fusion reactor. The box is now almost the same as that in the RetroFit puzzle except the hole in the cover is smaller. The coordinate motion move is the reverse of what happens in RetroFit. The puzzle also features moves with some resemblance to disentanglement puzzles. There are three other normal apparent solutions in this puzzle which are not possible due to the cover. The construction of this puzzle is solid, with excellent box joinery and every internal piece milled from solid wood."


Made in England, 1923.
(5.25 by 5.25 by 9/16 inch cardboard box and 15 wood pieces;
shown on page 131 of the Fifteen book, where it is dated;
Hordern's book also dates this puzzle and presents an 81 move solution)





Patented by R. Shaffer 1900, made early 1900's.
(top left: metal 1.6 by 3.5 inches,
"THE PERPLEXING PUZZLE, SPELLS, PERPLEXITY, PATENTED";
lower left: metal 1.75 by 4.2 inches, "AUTOMOBILE, PATENTED";
top right: metal 1.6 by 4 inches,
"WHEN YOU ARE DOWN IN THE MOUTH, THINK OF JONAH, PATENTED, HE GOT OUT";
lower right: metal 1.6 by 4 inches with paper sleeve,
"SOUVENIR PANAMA EXPOSITION 1915, R.E. ROSS PHILA.PA., PANAMA CANAL, PATD")
Some buttons are smaller with off-center shafts. As described above in the directions on the paper sleeve in which The Panama Canal came (its first button is "The"), generally, when the upper and lower slots are full, buttons cannot be parked on the vertical legs and still allow buttons to pass by horizontally, and when there are three buttons on the left, a button cannot enter the lower vertical leg. However, if things are done just right, a button can be rotated and parked in the lower vertical leg while there are three buttons to the left. Hordern's book describes a solution for Perplexity (using key letters XIRY), a solution for Automobile (using key letters BOOT or TILE), and mentions another version for the Louisiana Purchase Exposition in 1904.
Further Reading
Shaffer Patent, from: www.uspto.gov - patent no. 642,374

Unknown manufacture.
(wood, 3 by 4.75 by 1.25 inches)
This puzzle works in the theme of the Perplexity Puzzles, but rotation of buttons is not an issue as with those puzzles. The box can be turned over to play the 27 puzzle, on the other side:





Saleable Products, Los Angeles CA, design patent 1945.
(5.75" x 5.75" x 1.25" cardboard box with 5.5" x 5.25" x 1.25" puzzle)
Shown on plate XII, and pages 172-173, 228 of Hordern's book, which presents this solution:Notation: A1&A2 = left train, B1&B2 = right train, L, R, S = left, right, side tracksFurther Reading
A1 goes to R, A1 backs into S (pushing the freight cars to make room)
B1 & B2 go to L and attach to A2
A1 goes to R
B1 & B2 pull A2 to R, B1 & B2 push A2 into S, B1 & B2 detach from A2 and go to L
A1 backs into S and attaches to A2, A1 & A2 go into R
Sewell Design Patent, from: www.uspto.gov - patent no. D140,371

Patented by M. Fritsche 1986.
(plastic, 2.5 by 3.25 by 3/8 inches)
Two rings each contain seven discs each (six at 60 degree increments around the edge and one in the center) and overlap by three discs (the center and two others) so that they can be turned to mix up the puzzle. The goal is to restore the pattern of a top row of three red, a middle row of four yellow, and a bottom row of three green, and the numbers on the rows of the reverse side (molded into the white plastic) being 123, 4567, 890:

Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/rotos.htm
Fritsche DD Patent, from: www.epo.org - patent no. 236263



a.k.a. Turnstile, Twinspin, Engels Engima
Patented by D. A. Engel 1983, copyright GO Images Inc. 1986.
(plastic with cover, 4.75 by 6.4 by 1/2 inch;
the photos above show the puzzle on top of the cover)
The directions below are on the back of each puzzle; Jaap's Page presents solutions.
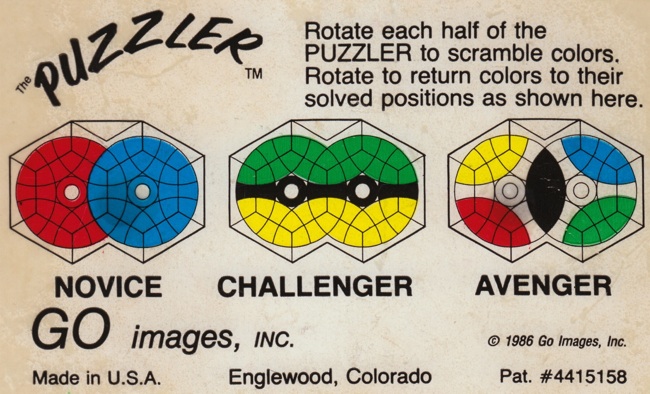
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles
Douglas Engels Solution Book, from: http://www.jaapsch.net/puzzles/circleman.htm
Engel Patent, from: www.uspto.gov - patent no. 4,415,158


a.k.a. Taquinoscope
Patented by Raoul Raba and copyright by Pentangle, England, 1977.
(plastic, 5.6 inches diameter by 1/8 inches thick;
front has three circles and back has Pentangle promotional graphics,
although sometimes this one was made with triangles on the back)
Three intersecting discs can rotate; the goal is to mix up the puzzle and restore it to the original pattern. Usually has a pattern of three circles on the back side and was made with different graphics on the front, including Concord plane (below), Marilyn Monroe (below), snake, serpent, wool mark, Sam Loyd, triangles containing figures. Jaap's Page presents a solution.






Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/rotascope.htm
Rabal FR Patents 7730347, FR2463632, FR2489164, FR2490102, from: www.epo.org
The puzzle came in a 1/4 inch thick flexible plastic case with a cardboard insert to hold it. The back of the case (shown below) describes the puzzle, gives some solution hints, mentions some puzzle history with regards to the Fifteen puzzle and Rubik's Cube, and shows copyright information.


a.k.a. Towers Of Hanoi Puzzle
Made by Oleg Raschkov, Germany, sold by the Puzzle Shop, 2018.
(plastic, 2 x 2.9 x 1/2 inches)
The two discs can rotate and exchange portions; kind of a more complicated version of the Rotascope puzzle. Jaap's Page describes solutions for three color scheme variations of this puzzle, the second of which is the one shown here. Here is the back:

Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/rashkey.htm



a.k.a. Rubik's Rings
Designed by E. Pap, made by Politoys in Hungary, 1982.
(left, plastic, 3.1 by 4.9 by 1/2 inches,
right is identical to left but with different colored balls,
bottom version circa 2000 is 3-dimensional but works the same way)
An old puzzle similar to this (the Race War Puzzle), with 22 balls in a ring and each ring one color, is shown on Page 131 of the Slocum and Sonneveld Fifteen book, and the mechanism is presented in the 1892 patent of W. Churchill.
Further Reading
Jaap's Page, from: www.geocities.com/jaapsch/puzzles/rings.htm
Churchill Patent, from: www.uspto.gov - patent no. 507,215

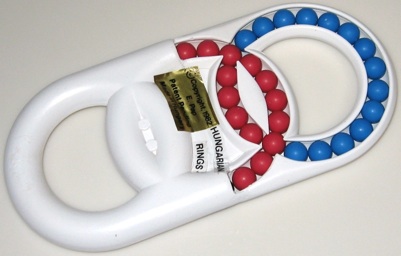
Designed and made by E. Pap, circa 1982.
(left: plastic, 3.1 by 6.8 by 1/2 inches,
right: plastic, 3.1 by 6.7 by 5/8 inches)
E. Pap made a number of designs in the early 1980's for generalizing the standard Hungarian Rings puzzle to three rings, two of which are shown above. Although it is not hard to see that they have been custom made, they both work quite smoothly. On the left is a straightforward generalization, and the one on the right is a "half-blind" version where one can only see half of the puzzle at a time and has to flip it over to see the other half; here is the other side:


Designed and made by E. Pap circa 1982.
(plastic, 4.9 by 5.7 by 5/8 inches pieces)
A generalization of the standard Hungarian Rings puzzle. This puzzle has a definite "prototype" feel to it, and if you turn it upside-down and shake you can get a ball to fall out (handy if you get tired of trying to solve it).


Produced in Hungary circa 1990's?
(plastic, 3.25 by 7.8 by 1/2 inches)
This generalization of the standard Hungarian Rings was also mass produced, but is harder to find as a collectible. The two shown above use the same set of colors, but have different numbers of each. The top one has 15 red, 15 blue, 14 green, 14 yellow, and 14 black, and the bottom one has 14 red, 14 green, 15 blue, 14 yellow, and 15 black.
The top one is solved as the two ring puzzle on the right with the other three rings attached; this allows for a solution that first uses the right two rings for "scratch space" to systematically solve the left three, and then solve the right two as with the standard two ring puzzle. In contrast, the bottom one shows a symmetric solution with the two 15 ball rings on each end. Both of these puzzles can be solved to have the black ring in the center as in the standard Olympic flag configuration; however, the bottom one will not have the correct overlapping pattern that requires the black ring in the middle to go under two other rings:


Designed and made by Diniar Namdarian 2012.
(laser cut plastic, plastic balls, and brass screws, 2.9" x 5.7" x 5/8";
mix up and restore to the position shown in the photo)


Designed by Josh Frankel, copyright Binary Arts 1998, made in China.
(plastic, 3.6 inches diameter by 5/8 inches thick)
Arrange the balls in numerical order. The balls can be cycled through the gaps at both ends, which are set back from the ends by one ball (so the order of the balls can be changed by parking and unparking balls at the ends as they are cycled). This puzzle ends up being as more of a dexterity puzzle than a logical one. Diamond Bob's Billiards Nine Ball Diamond Bob's Billiards Nine Ball is a harder puzzle in this theme.


Designed by Josh Frankel, copyright Binary Arts 1998, made in China.
(plastic, 3.6 inches diameter by 5/8 inches thick)
The puzzle has a circular track that can hold 9 discs and a track across the center that can hold two additional discs. The track across the center is actually Y-shaped, but this is just to make the piece fit well. The basic operations are to rotate the circle of discs, or to move a disc into or out of the center track (so there are a total of 10 discs and a gap, and at any time the circle has 10 discs and center track 1 disc, or the circle has 9 discs and the center track 2 discs). The goal is to mix up the puzzle and then restore it to the solved position where the discs numbered 1 to 9 are in numerical order around the circle and the white disc is in the center. Jaap's Page presents two different solution methods. A much easier puzzle in this theme is Diamond Bob's Billiards.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/nineball.htm

Made by Clever Toys, purchased 2007.
(wood, 4.75 inch diameter by 7/8 inches thick)
Three circles containing seven balls each, with a central turntable that simultaneously rotates sets of three balls between the circles. A simplier version of the Trio puzzle.

Made by Clever Toys, purchased 2007.
(wood, 5.25 inches by 7/8 inches thick)
Three circles containing ten balls each, with a central turntable that simultaneously rotates sets of for balls between the circles; in each of the circles, two of the balls are joined. Jaap's Page presents a solution.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/trio.htm

Made by Clever Toys, purchased 2007.
(wood, 5.25 inches by 7/8 inches thick)
Three circles containing ten balls each, arranged in five joined pairs, with a central turntable that simultaneously rotates sets of four balls between the circles. A version of the Trio puzzle where all balls are part of a pair.

a.k.a. Motyl
Made by Clever Toys, purchased 2007.
(wood, 5 inches by 7/8 inches thick)
Two rings each capable of holding 18 balls, with a central portion that moves 4 balls between the rings (there are a total of 32 balls); there a total of seven pairs of balls that are joined. The central portion has thick bars on each side constructed in a way so that when one ring is complete and can rotate, the other ring cannot move (and its balls cannot fall out). The balls are arranged in an alternating pattern of single ball and joined balls, and because the bar can only contain one pair at a time (because two pairs separated by a single ball would be 5 long), this alternating pattern is always maintained as the puzzle is mixed up. The goal is to mix it up and then restore the pattern shown above (yellow at one end, light brown in the vertical sections, and dark brown at the other end). Jaap's Page presents a solution.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/trio.htm
Copyright 2008 Aubrey Hearn.
(An Apple iPhone App available in 2010.)
This fun Apple iPhone App lets one solve 100 levels of puzzles. Below are levels 1, 2, 10, and 25. For all levels, a colored dot can only move along and edge of the same color, and the goal is to move the red dot with the subway car to inside the red goal circle. The following pages show the 589 move solution for level 100, shown above.
Problem 1, 3 moves.
Problem 2, 10 moves.
Problem 10, 16 moves.
Problem 25, 29 moves.


W. C. Horn, Bro. & Co. NY. "Manufacturers Since 1846", not dated.
(cardboard box, wood board, and painted wood pegs, 2 by 7 by 5/8 inches)
This old design is discussed on the Elliott Avedon Museum page. Exchange the two colors by successive moves of either moving a piece forward to an adjacent empty square or jumping forward a single piece of the opposite color:The 1942 Filipiak book presents the following 24 move solution: Except for the left and right ends, two adjacent of the same color leaves you stuck. So at any point, you have only one choice that does not quickly create this situation. This reasoning leads to the 24 move solution above, which can be viewed as increasing sequences of alternating colors followed by decreasing sequences, that works in 8 phases:
Except for the left and right ends, two adjacent of the same color leaves you stuck. So at any point, you have only one choice that does not quickly create this situation. This reasoning leads to the 24 move solution above, which can be viewed as increasing sequences of alternating colors followed by decreasing sequences, that works in 8 phases:
Move left.
Jump right.
Move right.
Jump left.
Jump left.
Move left.Jump right.
Jump right.
Jump right.
Move right.
Jump left.
Jump left.Jump left.
Jump left.
Move right.
Jump right.
Jump right.
Jump right.Move left.
Jump left.
Jump left.
Move right.
Jump right.
Move right.
Further reading:
Elliott Avedon Page (Map Games), from: http://www.gamesmuseum.uwaterloo.ca


TeeZ by K-T games, Sayville, L.I. N.Y., copyright 1954;
Brainbuster by International Games of Canada Ltd.
(both plastic, 5 blue and 5 red pegs on a 2 by 6 inch board;
TeeZ from the house of J.A. Storer's parents))
A larger version of the Eight Peg puzzle. The red and blue pegs must be exchanged by only moving blue right by one or hopping one and red left by one or hopping one. Here are the TeeZ puzzle and directions from the back of its box:


Like the Eight Peg puzzle, except for the left and right ends, two adjacent of the same color leaves you stuck. So at any point, you have only one choice that does not quickly create this situation. This leads to a solution of 35 moves, with increasing sequences of alternating colors followed by decreasing sequences, that can be viewed as working in 10 phases (delete phases 5 and 6 and you have the solution to the Eight Peg Puzzle):


Lubbers & Bell Mfg. Co., Clinton, Iowa;
top is 1922 First Edition, bottom is 1929 Fifth Edition.
(cardboard box 6.7" square by 1.2" thick, booklet, wood board, and wood pegs)
Starting with a peg in every hole but the center, hop the pieces over each other (like checkers) to remove them so that all that remains is a single peg in the center. The booklet that comes with the puzzles gives additional problems based on different starting positions.
Further Reading
1922 Peg Puzzle Booklet.
1929 Peg Puzzle Booklet.


a.k.a. Downsize
Binary Arts, circa 2000.
(plastic box, 12 pieces, 40 problem cards, 4.25 by 1.5 inches)
The board has 13 spots on which pieces can be initially placed. The goal is to remove all but one of the pieces by hopping them off (hopping over a piece removes it). Downsize is the same puzzle with the same cards, but different graphics. The 40 puzzles cards, rated from beginner to expert, including problems where the position of the final piece is specified. For example, here is the front and back of Card 40:



Patented by F. Lammertink 1989, made by Binary Arts.
(left "Top Spin", right "No. Crunch"; both plastic, 6 inches)
Numbers slide around the loop, and spinning the disc reverses the order of 4 numbers; the goal is to mix up and then restore to increasing clockwise order.
Notation:R = rotate the numbers right (clockwise) one positionSolution from the directions:
L = rotate the numbers left (counter-clockwise) one position
S = spin the disc (180 degrees)Note: S advances one number 3 positions clockwise, one number 1 position clockwise, one number 1 position counter-clockwise, and one number 3 positions counter-clockwise.
- Solve 7 to 20 by working from 19 down to 7, one number at a time:
A. Advance 3 positions clockwise until within 4 positions of destination.
B. Move counter-clockwise until exactly four units from destination.
C. Spin the disc.
- Get positions 1 to 6 as close to solved as you can.
- The following transformation advances a number in the left position of the disc 4 positions clockwise without affecting any other numbers:
S L S R S L S (That is, LRL with interspersed S's.)So to exchange two adjacent numbers, repeat this sequence 5 times to make a number go all the way around and come back exactly one position to its right (remember each time to put the number in the left position of the disc).
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/topspin.htm
Lammertink Patent, from: www.uspto.gov - patent no. 4,871,173
Cutrofello Patent, from: www.uspto.gov - patent no. 7,604,234
Chang Patent, from: www.uspto.gov - patent no. 5,622,368
Protheroe Patent, from: www.uspto.gov - patent no. 332,211










a.k.a. Tom's Turnstile
Copyright Brainwright, a division of Ceaco, 2016;
U.S. Patent 7,604,234 of Tom Cutrofello, 2009.
(plastic: 2 x 2.25 x 5/8 inches;
brass version: 2 x 2.25 x 5/8 inches, 6.1 ounces; box is 4 x 4 x 2 inches)
Two discs connected by a gear on the back, that spin together by turning the knob; similar but different from the Top Spin puzzle. Easy to rotate the discs, a bit slow to slide the numbers due to the small size (but it fits nicely into a pocket). The basic moves are:Shift all pieces one position right (clockwise) or left (counter-clockwise).It is tempting to argue parity for the number of exchanges in a solution, but since the pieces lie on a cycle and not a line, every piece is both ahead of and behind every other, and it is possible to exchange just two adjacent pieces and leave the rest of the puzzle the same (as shown in the photo above); call that transformation SWAP. Hence, solving is always possible from any permutation (although from any given permutation, faster solutions may be possible):
Flip the discs to change four consecutive pieces from ABCD to BADC.Phase 1: Consider 12 solved. Then, starting with 11 in the rightmost position, successively move 11 right one position with a shift left followed by a flip, until 11 is next to 12. Then repeat this for 10, 9, ... 5.
Phase 2: The final four can always be rearranged using successive swaps. For example, starting with 4321, swap(43), swap(42), swap(41), swap(32), swap(31), swap(21) results in 1234 (or, using only two swaps do flip, swap(41), flip, swap(32)).
Computer search found this SWAP sequence; R denotes move right (clockwise), L denotes move left (counterclockwise), and F denotes flip, and the letters 0,A,B stand for 10,11,12:

The existence of a SWAP sequence means that all permutations are possible and the solution method proposed on the previous page is well defined. Phase 1 placement of numbers 5 through 12 is straightforward, although it could be shorter for a given permutation. An interesting general question is to improve Phase 2 to fix the final 4 in a way faster than "brute force" use of SWAP. For example, the previous page noted that a final 4 of 4321 can be fixed with 2 flips and two SWAPs, for a total of 66 moves. However, it can be done in only 18 moves:

Computer search for all 24 permutations found that on average about 22.12 moves are needed to fix the final 4; here is a table of the lengths found for each permutation:
A natural task for this puzzle is to reverse the the numbers. After doing your best, compare the number of steps used to the sequence below, found by computer search, to convert the reversed sequence back to the original one. Note that this sequence is only 9 steps more than the minimum number of steps for a single SWAP.
One can imagine Turnstyle with a smaller number of pieces, and consider what sizes have the property that any permutation can be reached; i.e., for which a SWAP is possible.
Computer search shows that a SWAP is not possible for sizes less than 8, and also that it is not possible for puzzles of size 9 and 11.
Here are SWAP sequences for puzzles of sizes 8 and 10, where R denotes move right, L denotes move left, and F denotes flip, and the letters 0,A,B stand for 10,11,12.
Puzzle of size 8:

Puzzle of size 10:

Define JUMP4 to advance a pair of pieces right past 4 pieces; it can be implemented in 10 moves (the discs are in bold face, L = shift left, R = shift right, F = flip):

Define JUMP6 by using the first 8 moves of a JUMP4 followed by 8 additional moves to advance a pair of pieces right past 6 pieces:

Now consider a puzzle of size 14. A SWAP can be implemented by the sequence for 10 pieces presented earlier and using JUMP4 sequences to keep the turntable in the "zone" of 10 positions. That is, call the positions initially under the turntable EF, the four positions to the left of the turntable ABCD and the positions to the right of the turntable GHIJ, and use the SWAP sequence for 10 pieces to SWAP the pieces in position EF, with the modification that whenever shift operations cause the turntable to be at positions AB and the next operation is a shift left, then first do a JUMP4 on positions IJ, and whenever shift operations cause the turntable to be at positions IJ and the next operation is a shift right, then first do a reverse JUMP4 on position AB.
Similarly, SWAP for 12 pieces combined with JUMP4 gives SWAP for 16 pieces, and SWAP for 12 pieces combined with JUMP6 gives SWAP for 18 pieces. Doing the jumps in pairs gives swaps for 20, 22, 24 pieces, in triples gives swaps for 26, 28 30 pieces, and so on, to conclude that SWAP is possible for any even number of pieces of 8 or more.
Of course a shortest solution for a given permutation that may be much more efficient than a sequence of SWAPS.
Given that SWAP is not possible for sizes 9 and 11 but it is for sizes 8, 10, and 12, an interesting question is whether SWAP is not possible for puzzles of odd size.

Siebenstein - Spiele, Germany, circa 2010.
(wood and plastic, 1.2" x 8.1" x 11/16")
There are 7 unit size tokens labeled 1, 2, 3, 6, 7, 8, 9, and two 1x2 tokens, one labeled 4-5 and one labeled "LineArt". One 1x2 piece or two unit size pieces can be parked in the center above or below the middle row by sliding the center disc up or down. The middle row of 9 units can be slide so that any two positions are in the slider. The task is to mix things up and then put back to the solved position shown above.

Siebenstein - Spiele 2012.
(Wood and plastic, 3.4" x 6" x 1/2" body
with 8.5" long sliders made from 1/4" thick wood.)
The discs can be moved by tilting the puzzle, and one can prevent a disc from moving with a finger in the horizontal opening in the plastic. The task is to mix up and then arrange the discs so that the colors line up in pairs, with the pieces with the stars in the center on the bottom row. The discs are made with woods of different colors, but are hard to tell apart; this puzzle has color added along the rim of each disc to match the directions.





a.k.a. Zauberkreuz
Patented by A. Margaritis 1988.
(plastic, 5.75 inches by 3/4 inches thick)
The cross, where each direction is 2 units wide by 10 units long, contains 20 plastic tiles One diagonal half of each tile has a raised colored triangle (five each of red, blue, green, yellow, and black tiles). The two horizontal rows of six tiles each can slide together left or right one or two units, and similarly the two vertical columns of two tiles each can slide together up or down one or two units. Two clear plastic plates that are hooked into the openings in the bottom of the tracks (where one passes over the other) slide with the tiles to make them move together and prevent them from falling out The goal is to mix up the puzzle and then restore it to a pattern of five diamonds (or one of the other patterns shown on the back of the package). Jaap's Page presents move sequences to solve the puzzle that exchange pairs of tiles without disturbing the others (and he notes that this puzzle was sold on the 125th anniversary of the Red Cross). The solution is not unique; any color diamond can go in any position. In fact, once solved, it is easy to permute the diamonds by using only moves that slide two units at a time. For example, down two, right two, up two, left two cycles the upper left three diamonds (combine symmetric versions of this transformation to achieve different permutations of the diamonds).
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles
Margaritis DE Patent, from: www.epo.org - patent no. DE3711368

a.k.a. Rubik's Fifteen
Patented by E. Rubik 1984, copyright Matchbox 1990.
(plastic, 4.4 inches square by 3/8 inch thick)
The top side of the puzzle shown above has a 5 by 5 grid where the solved state has the numbers 1 through 16 (actually 1 through 15 and a star) arranged in row major order in the lower right 4 by 4 portion of the grid. There are three vertical plungers and three horizontal plungers. The vertical plungers can each be moved at any time to shift one of the middle three columns up or down one unit. The horizontal plungers are arranged with one for the top row, one for the bottom row, and a single one that simultaneously moves the middle three rows. In addition, the top and bottom plungers are constrained so that the top will only operate when all three vertical plungers are up, and the bottom will only operate when all three vertical plungers are down. The back of the tiles are yellow with numbers on them, and the back side of the puzzle has a 3 by 3 grid (centered in the puzzle) in which the solved state is to make a magic square of nine numbers (the sum of all rows, columns, and the two diagonals is the same). Jaap's Page presents a solution which can be used for both sides, and gives a table of all possible magic squares that can be made on the back. Tsukuda's Square and Uribock are similar puzzles with a different arrangement of plungers.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/rubik15.htm
McFarren's Page, from: http://www.geocities.com/abcmcfarren/math/r90/xvintro.htm
Wikipedia Magic Square Page, from: http://en.wikipedia.org/wiki/Magic_square
Rubik Patent, from: www.uspto.gov - patent no. 4,471,959

a.k.a. "It", 4x4 Four By Four Puzzle
Patented by T. Suga, 1983, copyright Gabriel Industries 1981.
(plastic, 3.5 inches square by 5/16 inch thick)
The back of the box in which the puzzle came challenges one to arrange the 4x4 array of tiles to form one of the four patterns shown below. There is a plunger on the top that can slide the rightmost three columns down one unit simultaneously, and four plungers on the left that can slide each of the four rows horizontally one unit to the right (any combination of plungers can be used except that the first of these four cannot be pushed if the top plunger is already pushed); the plungers are located on the back of the puzzle (see photo below) and have springs that cause them to snap back when you let go. So this is really a 5x5 grid with the empty left column and empty top row hidden. Rubik's XV and Uriblock are a similar idea, except with a different arrangement of plungers that do not have springs (and where for Rubik XV the empty column and row can be seen). The Four By Four version of this puzzle was made with the same graphics and also in a version with a picture of a lion, and the "It" version was made with the numbers 1 through 16. Jaap's Page presents a solution that has four simple sequences to cycle 7 tiles (two rows less a corner) in four ways (clockwise or counter clockwise, leaving out either an upper left or upper right corner), uses them to solve the first two rows and some of the bottom two rows, and then employs complicated combinations of these sequences to solve the remaining tiles.


Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/it.htm
Suga GB Patent, from: - http://www.ipo.gov.uk patent no. GB2,101,897

a.k.a. Mix Box
Brevettato (patented), Italy, circa 1980's
(cardboard box and plastic puzzle, 5 inches by 7/17 inches thick)
A 4 by 4 grid can be manipulated by sliding the rows and columns by one square. The top row can only move one square to the right, the second row one square to the left, the third row one square to the right, and the fourth row one square to the left. Similarly, the left column can only move one square up, the second column one square down, the third column one square up, and the fourth column square down. Mix it up and then solve to one of the patterns that are shown in the directions that were sold with the puzzle:

This puzzle is similar to Rubik's XV and Tsukuda's Square. Jaap's Page presents a solution that first observes that a local permutation of three squares can be achieved by the sequences of four moves consisting of sliding a row, a column, the row back, and the column back, and then solves by first placing the four corners and then repeatedly using this transformation to solve the remaining squares.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/uriblock.htm


Patented by G. Yokoi 1983.
(plastic, 3.5 inch diameter with arm, 3/4" thick,
with box 4.4 inches square by 1.2 inches high)
The puzzle comes in a plastic box as shown below; the Yoki patent also describes the Ten Billion Barrel puzzle. Seventeen pieces (one white and four each of orange, green, blue, and yellow) are arrange in a cross (a center piece and four pieces on each arm). A center disc can rotate the center five pieces (i.e., the center piece and the first piece on each arm), a middle ring can rotate the next two pieces of each arm, and an outer ring can rotate the outside pieces of each arm. In addition, a plunger can be temporarily pushed in to offset all of the pieces of a row by one unit (and while it is in, the outer ring cannot rotate). The goal is to mix up the puzzle and then solve it so that each concentric circle has the same color (with white in the center). Jaap's Page credits the puzzle invention to work at Nintendo and presents a solution.

Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/trillion.htm
Yokoi Patent, from: www.uspto.gov - patent no. 4,376,537


Patented by F. Lammertink 1996, copyright Binary Arts 1995.
(plastic, 4 inches by 6.25 inches by 7/8 inches thick)
The central portion of the puzzle is a 2 by 7 array of tiles, which can slide left or right by one unit. In addition, there are a pair of plungers that each have an array of 3 by 2 tiles where 4 of them intersect the main 2 by 7 array at columns 2 & 3 and columns 5 & 6. Pushing on them reverses which one is up and which one is down (i.e., when one is down the other is up). The goal for Port To Port is to move the boat from one side to the other. The goal for Triple Cross is to form a line and circle (or to start with an easier challenge of just binary arts tiles together, just the line, or just the circle); here is a photo of a gray body version mixed up:

The directions that were sold with Port To Port give a 30 step solution, and the directions that were sold with Trip Cross describe basic move sequences. Jaap's Page presents a solutions for both puzzles.

Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/port.htm
Lammertink Patent, from: www.uspto.gov - patent no. 5,542,673

Made by Binary Arts, 1994.
(plastic, 6.5 inches by 7.1 inches by 1 inch thick)
Slide rows left and right by one unit (by pushing on the ends of the rows under the left and right edges of the puzzle), tipping and rolling marbles so as to position them to match one of the 52 patterns suggested in the booklet that comes with the puzzle; four of these patterns are shown on the top and bottom edges of the puzzle.

Patented by G. Pahud 2005, purchased from www.swissmad.ch.
(plastic, 3.25 inches square by 3/8 inch thick)
A cross of 12 squares visible on both sides, where each side of each square is colored red or white (there are exactly three squares of each of the four possible combinations of red and white). The front has ridges on two of the center squares that can be used to slide each of the two columns up or down by one square and the back has ridges on the other two center squares that can be used to slide each of the two rows left or right by one square. The directions have the eight patterns shown below (this one came with Diversity on the front and Time on the back).
Jaap's Page observes that a simple sequence of 4 moves to cycle three squares (column down, row right, column up, row left) can be repeatedly used to solve the puzzle (except that at the end you may have to replace a square with an identical square to fix a parity problem), and lists which combinations of these eight patterns can be solved simultaneously on the front and back (possibly rotated by 90 degrees); Interaction and Balance can be solved on the front with any of the 8 patterns on the back, Time and Excellence with any except Mutual Help (and Mutual Help with any but Time and Excellence), and Diversity, Audacity, and Security with any of the other 5.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/swissmad.htm
Pahud WO Patent, from: www.epo.org - patent no. WO2005/053809



Designed and produced by Jean Claude Constantin, 2011,
presented at IPP 31, and also sold by Puzzle Master.
(1/8" thick clear plastic over laser cut pieces in 3/8" plywood base, 5.5" x 5.5" x 1/2";
front and back of directions sheet shown above)

a.k.a. Twisting Tri-Side Puzzle
Patented by Heng-Chun Ku 2000, copyright Playroom Entertainment 2002,
Made by Dah Yang Toy Industrial Co., China.
(plastic, 5 inches)
Turn the knobs to rotate a circle of six triangles. Mix up the puzzle and then restore it to six colored wheels as shown above, or make different patterns such as those shown below. Jaap's Page presents a solution.
Further Reading
Jaap's Page, from: http://www.jaapsch.net/puzzles/madtriad.htm
Ku Patent, from: www.uspto.gov - patent no. 6,022,021

a.k.a. Twisting Tri-Side Puzzle
Smaller version of the Mad Triad, same orgin of manufacture.
(plastic, 4 inches by 5 inches by 1 inch thick)
Here are some other patterns to make:
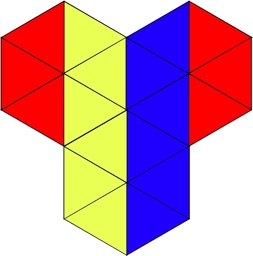
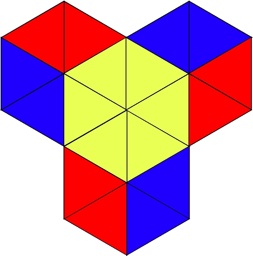

Designed and made by Robrecht Louage, purchased from Cubic Dissection 2009.
(milled from stainless steel, Corian, and acrylic, 4 by 6.25 by 5/8 inches)
Five vertical rods can be shifted up and down by one unit to allow two flat stainless steel plates with unit size teeth on them to slide out to the left. Here is a view of the initial position in which the puzzle was sold:




Designed and sold by David Litwin, 2012.
(laser cut plastic and stainless steel screws, 5.5" tip to tip, 3/4" thick)
This puzzle is beautifully custom made from layers of laser cut plastic. A middle plunger that moves horizontally is crossed by left and right plungers that form an X. The plungers can be moved to rearrange the gold tiles in the center that contain a circle pattern. Here is an example sequence of moves (that corresponds to a left rotation shown on the following page):





As shown below, moving the plunger in the wrong direction leaves the puzzle "locked" so that that plunger must be moved back to where it was. However, as shown on the following page, in any of the three orientations, there are three rotation sequences, each with a clockwise and counterclockwise version, that can be used to mix up the tiles, and then restore the circle pattern. A fun puzzle that is harder than it looks at first.

Left Rotation Sequences:Left: Rotate (1,2), (3,4), (X,Y) clockwise; that is:Right Rotation Sequences:Move middle RIGHT, right UP, middle LEFT, right DOWN.Left CC: Rotate (1,2), (3,4), (X,Y) counterclockwise; that is:Move right UP, middle RIGHT, right DOWN, middle LEFT.Right: Rotate (2,3), (4,5), (Y,Z) clockwise; that is:Center Rotation Sequences:Move left UP, middle LEFT, left DOWN, middle RIGHT.Right CC: Rotate (2,3), (4,5), (Y,Z) counterclockwise; that is:Move middle LEFT, left UP, middle RIGHT, left DOWN.Center: Rotate A,B,3 and rotate 2,4,Y clockwise; that is:Move right DOWN, left DOWN, right UP, left UPCenter CC: Rotate A,B,3 and rotate 2,4,Y counterclockwise; that is:Move left DOWN, right DOWN, left UP, right UP.



Designed and sold by David Litwin, 2012.
(laser cut plastic and stainless steel screws, 5.5" tip to tip, 3/4" thick)
This puzzle is beautifully custom made from layers of laser cut plastic. It is a successor to the Elemental Neon puzzle, and like that puzzle:Here are photos of each of the three plungers moving (and for each, the plunger can also move in the opposite direction):
- A middle plunger that moves horizontally is crossed by left and right plungers.
- The plungers can be moved to rearrange the red tiles in the center through which a pattern of 4 circles can be seen; it helps to do this under a light so the pattern is easier to see:

- Rotations of the triangles to mix up the tiles; then restore the pattern.
- Fun to use and harder than it looks at first.






Copyright 2006,2009 Douglas A. Engel, made by Flatland Gear Works.
(plastic puzzle in cardboard box, 4" x 4.75" x 7/16")

String puzzles can be great for a coffee table because what is essentially the same puzzle can have great cosmetic variety, and most of these puzzles have most of the advantage of a manipulation puzzle. True, the object is often to remove a ring or something, but it is usually much easier to put it back than to remove it, and if you get tired, you can usually untie a knot, put the ring back on, and put the puzzle back on the coffee table (without needing a bag to hold multiple pieces). Wire puzzles usually involve two pieces that must be taken apart. Like, string puzzles, wire puzzles can be great for a coffee table because what is essentially the same puzzle can have great cosmetic variety, and for most of these puzzles it is much easier to put the pieces back together than to take them apart (so you can put it back on the cofffee table).

Old design, this one purchased circa 1995
(steel, 12.75 inches)
To take the ring off, push the horse shoes together while twisting at the same time, so that they line up and the ring can come off (and reverse this idea to put it back on); here are photos of this process for the Wing It version of the puzzle:




"Wing It", copyright ThinkFun 2003.
(metal and plastic, 5.5 inches, 2.25" diameter ring)

a.k.a. Ball And Chain
Old design, this one made by J. Storer, 1990.
(wood block, steel ring, and copper tubing, main loop is 6", block is 2.5", ring is 2")
The block fits through the big wire loop, but not the ring, and the ring can pass through the smaller wire loop. Once solved it seems easy, but come back a year later and it can mystify you. To get the ring off, pass it down through the metal loop at the base of the puzzle, around the end where the string is attached, and back up to the position shown in the figure below. Now continue the ring around the main loop and back through the loop at the base to come off. If you make a mistake, you can wrap the string twice around the ring rather than get it off!


a.k.a. Moving Beads, Tiger Cross, Wizzard Wedding Ring
Old design, these made by J. A. Storer, circa 1990.
(brass with nylon cord, both rods 9/16 diameter by 5.75 inches long)
This is an example of a moving bead puzzle (e.g., see Coffin's Puzzle Craft book). To solve, pull out the loop and move one ring through the loop and off to the side, pull the whole knot through the hole, pass the ring through, pull the knot back through, move the ring back through the loop and adjust everything to be centered again. This puzzle is often made to look more confusing in a way that does not change the solution, such as making the rings large enough to pass over the rod (first puzzle above) or adding extra hardware (second puzzle above, whether or not a bead can pass through the extra ring does not matter).

Old design, this one made by J. A. Storer, circa 1990.
(made from 1/4 inch aluminum plate and 3/4 inch diameter brass rod, 6.5 inches;
the design of this puzzle reflects the figure in Coffin's Puzzle Craft book)
The square fits through the slot but not the ring. The ball fits through the ring, but not the slot. The ring fits through the slot and can pass over the narrow end past the slot, but not over the wide end. The task is to remove the ring. It can seem easier to put the ring on; one can retie the string with only one loop around the middle and first learn how to put the ring on.
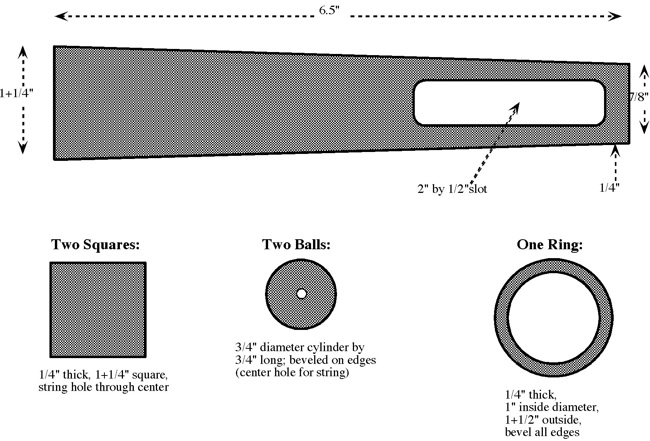
D. Barry has made STL files for a 3D printer:




You can instruct your browser to download these files (courtesy of D. Barry):Bar.stl
Ring.stl
Ball.stl
Square.stl
Further Reading
STL Wikipedia Page, from: http://en.wikipedia.org/wiki/STL_(file_format)

Purchaed circa 1970.
(wood with metal ring, 4 inches)
This is a simplier version of the Wit's End puzzle with only one loop around the puzzle body.

Patented by Robert Boomer 1968.
(metal and plastic, main piece is 3" high by 3" wide)
Take the ring off; here is the solution that was sold with the puzzle:

Family Games Inc. 2005.
(nylon cord, wood ball and block, 1/8" diameter metal wire, 6 inches)
Referring to the photo above, a left and right arm are joined along the bottom by a third wire piece. A cord goes from the ball, around the left arm, around the right arm, through the block to a ring. The block cannot pass through a ring but the ball can; however, it is only the ring on the right arm through which the ball passes in solving the puzzle (the ring on the lower right just serves to prevent one from flexing the right arm and passing the ring on the right arm around the bottom). The goal is to remove the ring from the right arm.
The solution passes the ball through the ring twice; first to get the ring from around the right arm to around the cord, and second to follow the cord out to the left and off over the ball. Here is the solution that came with the puzzle:

Old design.
(7/32" diameter steel, each piece is 1.75" by 2.25")
Perhaps the most basic wire puzzle; separate the two nails.

Purchased circa 2000.
(steel, 2 pieces, each U is 2.25 inches by 2.5 inches by 1 inch)
Separate the two pieces:


Purchased circa 2000.
(steel, 2 pieces, each piece is 5.5 inches long)
Separate the two pieces:


Purchased circa 2000.
(steel, 3 pieces, two that can't come apart, heart is 4" by 5", made from 1/4" rod)
Separate the heart from the remainder of the puzzle:




One of many in the Cast Puzzle series, Hanayama Co. 2007.
(metal, outside diameter 1.8 inches, inside diameter 1.1 inches;
the beveled ends of the two pieces have magnets in them)
The straightforward way to assemble the two pieces is to start with the two ends touching and twist counter clockwise. However this ends with the two beveled ends meeting backwards:


Instead, start with the inside ends of the two pieces meeting and twist clockwise, and the two bevels will meet properly to allow the magnets to snap the ring in place:




Copyright Hanayama Co. LTD 2000.
(steel, 2.25"; directions on the box back)


Cast Puzzles, Copyright Hanayma Co. 2008.
(metal, 2 inches)
Three spiral shaped pieces with carefully placed bumps and cuts on them (in different places for the three pieces) slide together. Although they feel loosly linked together when holding the puzzle assembled, the fit is very exact when dissassembling or assembling (a littly bit of force is required to make the puzzle spring loose on the first dissassembly step or back together on the last assembly step).

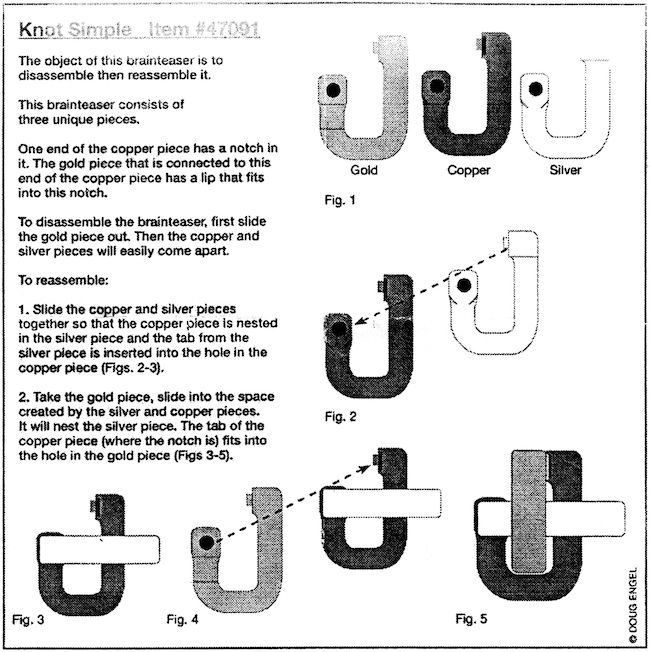
Made in China, 2011.
(three metal pieces, each is 2" long)

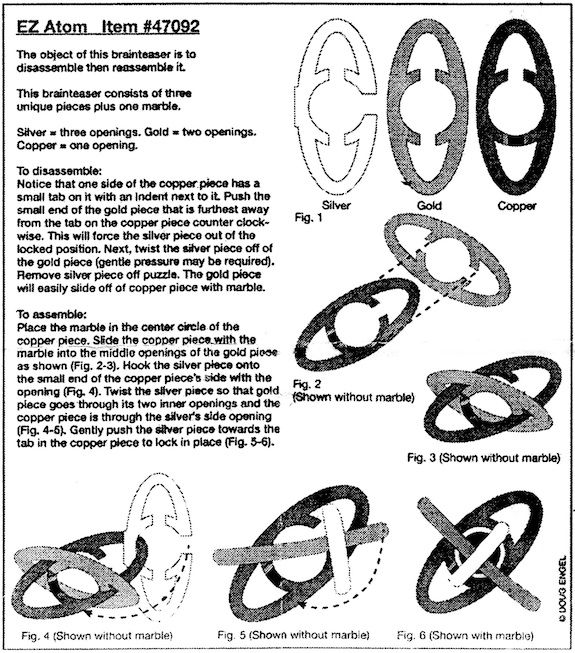
Made in China, 2011.
(three metal pieces and a glass ball, each piece is 3.2" long)

Purchased from Bits And Pieces, 2008.
(4 metal pieces, 2.5 inches square by 1/2 inch thick, with two page solution sheet)
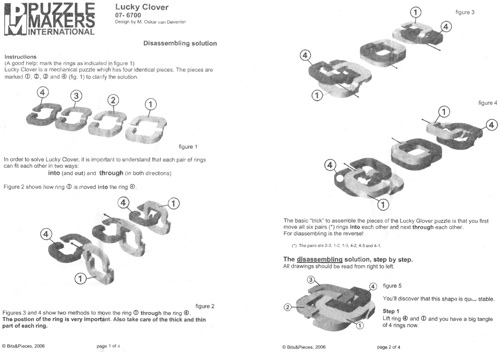


Old design, this one made by J. A. Storer, circa 1990.
(two brass pieces, one with nylon cord attached, 3/4 inch diameter, 3 inches long)
The task is to separate the loop (attached to the ball) from the brass rod. This is a basic example of an entangled loop puzzle (e.g., see Coffin's Puzzle Craft book). To solve, pass the end of the loop through the holes, arond the ball, and back through the holes.

Copyright James A. Storer 2009; U.S. patent 8,393,623 March 2013.
(Cherry with nylon cord, 1.5 inches square by 19.5 inches long)
A cord with knots is attached to one end; thread it so that no knots show. Here are views of the solution, where the rope visits the holes in the order 4, 5, 1, 2, 7, 3, 6, 8, 11, 9, 10, 12:



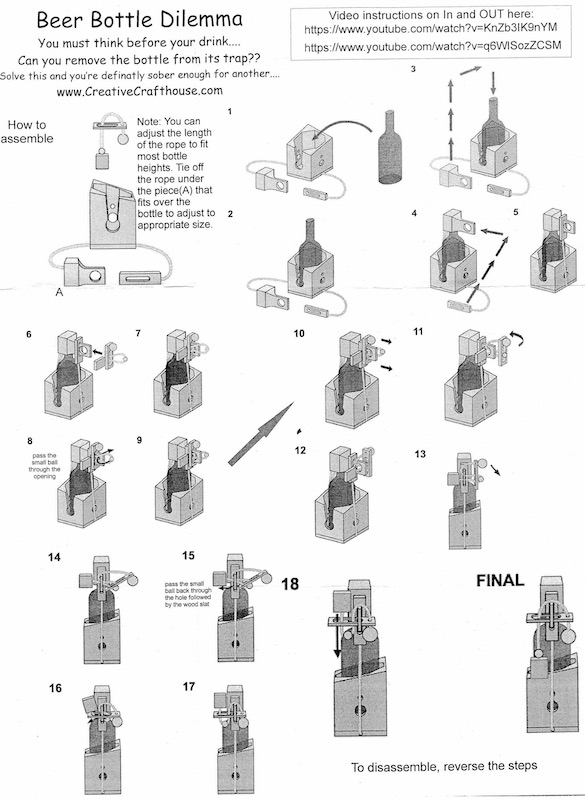
Creative Craft House, "Think Before You Drink", 2018.
(wood + standard beer bottle, 9.75" high with 3.25" square base; top assembly is 5" wide)
Manipulate the string puzzle in order to remove the bottle.

There are many other types of puzzles that have not been addressed here, of which I have a few. Most notably are dexterity puzzles (tilting to roll balls into positions, etc.), novelty and trick puzzles (getting something apart by shaking to move a secret pin, etc.), and puzzle boxes, which can be a combination of art, trick moves, difficult burr-like assemblies, etc.



a.k.a. Take It Apart
Patented by J. Boyle 1939.
(10 wood pieces and a penny, 3.25 inches sqaure by 11/16 inches thick)
The one on the top left says "PAT. PEND" on both the box and the puzzle, and the one on the top right shows the patent number on the puzzle. This puzzle was made for many years; J. A. Storer played with the third one above as a child in the 1960's. One must shake the internal pegs to a position that allows disassembly with a twist:

Further Reading
Boyle Patent, from: www.uspto.gov - patent no. 2,181,116

Designed by Charles Perry, 1989.
(three plastic pieces and 3 brass rods, 2 inches)
Separate the three plastic pieces from the three brass rods. Charles Perry is a well known architect and sculptor who has also designed some puzzles. The Charles O. Perry Puzzle Page shows a number of puzzles, including the Double Puzzle Page with a diagram of how it goes together:
Further Reading
Charles O. Perry Puzzle Page, from: http://www.charlesperry.com/puzzles
Double Puzzle Page, from: http://www.charlesperry.com/puzzles/double-puzzle

Purchased circa 1995.
(aluminum, 3.75 inches)
This puzzle at first appears to be made of two pieces, the post and the turret, that can wiggle a bit but won't come apart. However, the surface inside the turret can be pushed down against a spring. By holding the puzzle upside-down, and pushing in, the surface can spin until a brass pin inside can drop down and allow the turret to be unscrewed. Inside is a pawn:


Unknown original name ond manufacture; this one purchased circa 2000.
(wood with metal ball and bolt, 2.3 by 3.9 by 2.5 inches high;
object is to remove the ball)

a.k.a. Bougie, Get Charged
Available from a number of sources in 2013,
including Bits & Pieces and Puzzle Master,
who credit the design to Jean Claude Constantin.
(wood, metal pins, and spark plug, 3.75" x 2.2" x 1.1")
One of the metal rods is tight, whereas the other one wiggles. Position the puzzle as shown on the left below, so that the rod that wiggles is facing forward. Notice that if you look carefully, the hole that the rod goes into on the right is larger than the left. The puzzle will come apart by pushing the rod to the right, having the left end of the rod come out, and then angling the rod out of the frame (allowed by the larger hole on the right). While applying pressure on the front rod pushing it to the left, bang the puzzle hard down on a table; this causes a piece hidden in the right side to drop down, allowing the rod to be pushed further into the right and the left end to come out. The puzzle apart is shown on the right below.



Purchased circa 1995.
(aluminum and brass, 3 inches;
the object is to manipulate the post out of the cage)



Hanayama Cast Puzzle, purchased from Amazon.com, 2018.
(metal, 5 pieces, 1+7/8 inches long, nut heads are 1 inch between faces)
The little nut is not important to the puzzle; it is just something to store inside. When apart, both big nuts will thread all the way onto the two pieces. But to take the puzzle apart, the two pieces must slide apart when the missing threads on the big nuts line up exactly. There are some false seams so that the body appears to have 6 equal sections, when there are really only 4 sections. The puzzle is made quite difficult because it cannot slide apart all at once. irst things have to be lined up exactly to slide a bit and then exactly another way to slide further. After two such steps the nuts come apart enough to get the little nut out, but two more steps are need to get the pieces all the way apart. One approach is to start with the big nuts close to each end for the first two steps, and then closer to the middle for the next two steps; for each step, hold one end leaving the assembly hanging down and gently turn a nut to feel a slight release.

Made by Binary Arts, 2002.
(metal, 6.5 inches)
The car, with two pegs extending out the bottom, must be manipulated to travel between cities.

Hasbro Industries, 1972.
(plastic ball on stand with screws, 4.5 inches)
Put in all the screws. Here is what is on the side of the box:




R. Journet & Co. LTD London, sold by Abercrombie & Fitch, NY, circa 1930's?
(two cardboard storage boxes 5.5" x 8.5" x 4.5",
14 puzzles 4"x5"x3/4", 1 puzzle 4"x5"x15/16", 7 puzzles 4.25"x3.25"x11/16";
all have the same text on the back as shown on the right above,
except for different number in the lower right corner;
all puzzles are paper covered wood frame with glass top)

Further Reading
Rob's Puzzles Dexterity Page,, from: http://home.comcast.net/~stegmann/dexterity.htm
Wikipedia AF Page,, from: http://en.wikipedia.org/wiki/Abercrombie_&_Fitch
(The "Little Patients" Puzzle)


Made by R. Journet for The Infant's Hospital, Vincent Square, London, circa 1930?
(was sold with a cardboard cover showing the title The "Little Patients" Puzzle;
wood box with glass top, 4" x 5" x 1"; directions on the box bottom; see also
Infants' Hospital Puzzle, Dad's Puzzler - Exchange Version / Infants Hospital,
Infants' Hospital - The Magic Line, Infants' Hospital Jigsaw Puzzle)
Box must be manipulated so that little capsules each with a steel ball inside must be placed to stand upright in the holes (in the photo, a steel ball can be seen that has come out of a capsule with a worn out end). For information about R. Journet, see the Abercrombie & Fitch Dexterity Puzzles.

Copyright 1941.
(metal with clear top, 3.5 by 2.5 by 1/2 inch)
The goal is to get the six hoops onto Elsie's horns by shaking and tilting the puzzle. The copyright information is written along the bottom of the puzzle inside:



Copyright Reiss Games Inc., 1976.
(plastic, 3 inches square by 1.25 inches high)


Loncraine Broxton, 1998.
(plastic, 3.25 inches square by 11/16 inch high)

Copyright 1988, Quebarts Ltd., Trolbourne Ltd. Greenwich, England;
Patent Pending No. 8901362;
made by Binary Arts / ThinkFun late 1980's.
(metal springs and plastic, 6.5 inches)
Twist, tilt, and shake to get the six balls (2 red, 2 blue, and 2 yellow) to their proper ends. Although mainly a dexterity puzzle, it does take a little logic to route the balls, where it may be necessary to temporarily send a ball to the wrong location before sending it to its destination.



Designed by Michael McGinnis, Brian Clemens, and Dan Klitsner,
manufactured by Busy Life LLC and distributed by Spin Master LTD,
purchased from Amazon.com 2014.
(plastic, left - Original 6.5" diameter, right - Epic 7" diameter, bottom Twist - 6.5" diameter)
Fun 3D takes on the classic ball in the maze game.


Purchased by J. A. Storer in Costa Rica, 2003.
(wood, 8.5 by 5 by 2.4 inches)


Heartwood Creations, 1999.
(wood, 5.5 by 3.75 by 1.5 inches)

Designed and made by Stewart Coffin, 2014.
(wood, 3" face to face, both outer and inner puzzles are signed;
the inner puzzle is a variation of the Garnet;
one of 4 puzzles purchased during a visit with the designer in 2014)
Here is what the designer says in the directions that came with the puzzle:"Design X-48. This is a continuation of Double Play, begun with X-40, in which a Garnet is enclosed by a Scrambled Scorpius. Here the Super-Scrambled Version is used. The axis for the first step of disassembly coincides with the axis of symmetry of the light colored wood (maple). It is also marked by three pencil dots. No force or tools are required, just squeezing in the right places. Woods are maple, poplar, rosewood, and chakta. Joints are doweled. The Garnet is a new version, encountered here for the first time, and identified as the Double C, Three-Block Key. Woods are maple, poplar, kauri, lacewood, rosewood, and bocote. Five made in April, 2014."Because the inner puzzle is hollow, this puzzle can be viewed as a box inside a box. Here are phases of disassembly; numbers in the last photo are an order that pieces are removed from the inner puzzle (a steeper cut on an inside edge allows piece 3 to come out):







Designed and made by Robert Yarger, 2004.
(Oak exterior, Maple and Bloodwood mechanism, glass front, 13.75" x 5.5" 2.8")
A beautifully made (non-functional) grandfather clock has a sliding panel on the right side that in combination with sliding the bar on the front allows one to manipulate the hands with the goal to get them both to 12 and sliding the top forward to release the compartment out the bottom. This must be done with the clock on its back because gravity is need in combination with the gear shifting to get the gears to go between moving just one hand or both hands, and the puzzle tends to become a bit of a dexterity puzzle with some shaking and knocking.

Designed Robert Yarger 2002 (Stickman No. 1), and made by him in 2017.
(oak, 4.75 x 4.75 x 8 inches)
According to the maker:The first puzzle designed by artist Robert Yarger. These were limited in edition to just 100 puzzles, but the last 15 copies were not produced until now."Here are photos of the puzzle being solved:









Designed and made by Robert Yarger; purchased from Cubic Dissection 2006.
(Maple, Purpleheart, Wenge, 4.5 by 2.75 by 2.5 inches)
Ends and top pieces slide and levers move to expose either of two compartments.

a.k.a. Stickman No. 27
Designed and made by Robert Yarger, 2014.
(Ambrosia Maple / Redheart / Yellowheart, 6" x 8.25" x 6";
includes a 3.5" x 7.25" black and white booklet
with double sided cover, rear cover that is blank inside,
and 8 double sided internal pages.)
This puzzle is all about the key and lock. Disassembly begins by taking them apart into pieces that are used in other steps.
The following pages show the booklet that was sold with the puzzle with some notes at the end. Little or no force is necessary for any of the steps, but some steps do require some amount of force, and humidity could cause more resistance. Unless you are very experienced with puzzle boxes, it may be better to just appreciate the art and follow the directions the first time you disassemble it; otherwise, you may end up applying too much force when exploring possible move options, and possibly damage the puzzle.
DisassemblyAll steps:Reassembly NotesThe legs are firm when the puzzle is fully solved, but may be loose during disassembly. The puzzle came with a note that no attempt should ever be made to rotate any of the legs.Steps 1 & 2:The booklet says left knob but the figure shows turning the right knob. The knobs seem to spin and do nothing, but if you play with them you can get it so you can feel force on one when turning the other. I've found that the most repeatable way of pulling out the latch is to turn them both counterclockwise until the left one goes all the way back to 1 o'clock and will not turn further. Then the latch lifts up and out.Step 15:If the drawer will not move a full 1/4" as it is supposed to, it may be due to a problem that can arise with shipping it or when it is vibrated in a particular way. A butter knife can be used to fix this problem; here are directions that were emailed to owners:"If the drawer is stuck so it does not want to come out, insert a butter knife so that it is between the top of the drawer and the lifted up end panel of the box. The knife needs to go back at least 3”, and should be inserted on top of the drawer (on the “left” side). Then drag the knife across the top of the drawer to the right. There is an internal peg that will slide and stop against the front face of the box internally. Once done, the drawer should come out as per the instructions, and this step should never again be necessary, unless the puzzle is turned on its back side and vibrated."The puzzle designer sent email to caution the user about not using force:"The puzzle’s internal mechanics can be arranged in such a way that its lower removable compartment can be inserted backwards. In this configuration, (and with enough applied force), one of the hinge straps can then be manually pressed into an unintended locking position. If the compartment is put in backwards, you will eventually realize it and are able to backtrack (that is unless you also manually force hinge latches back into the box). The issue was always the hinge straps. When putting the puzzle back together, you can apply enough force to wedge internal mechanics apart and lock a hinge strap into place manually. This seemed like a logical assumption because that is the way latches on brief cases and suit cases relock. Just don't do this. The latches relock in the same way that they unlock, which is positioning things so they go in freely, then letting the internal mechanics engage them. Be mindful of how the straps eventually come out, so you can put them back in reverse order."


Designed and made by Robert Yarger (Stickman No. 30), 2017.
(leopardwood and walnut, with tamo burl tiles, 7.5 x 4.5 x 4.5 inches)
Here is a description provides by the maker:"This puzzle has a single hidden chamber, which can be accessed only after manipulating its tiles to complete intricate burl patterns on both sides of the box. Aside from the challenge of lining up tiles using little more than their intricate wood grain patterns as a guide, one end of this box also rotates. This allows tiles from one side of the box to be moved and exchanged with the other.
If that were not enough, a few rogue tiles are purposely rotated to be 90 degrees off from being able to match up with anything. A well-hidden trick must be discovered to resolve how to properly orient these tiles to line up with others to complete their patterns. For those who may find this exceptionally challenging, there are subtle clues that can also aid in proper placement of tiles - and of course there is always the solution book.
Finally, once the box is solved, its internal logic bars can be flipped over and re-inserted to create an entirely different puzzle solving process. This secondary solution requires just as much logical deduction as the primary method, but does not necessarily require that the patterns on both sides match.
In some ways this makes things easier, yet the challenge of the secondary method is that it locks certain tiles in place so that they no longer move until neighboring tiles are manipulated into proper positions. Manage to free a tile, and it is possible that its new position will indirectly lock yet another tile in place. The puzzle in this state can still be solved in the original way if desired, but flipping the logic bars adds an alternate secondary solution and provides other challenging components.
Limited in edition to only 50 completed boxes."


Designed and made with a 3D printer by Diniar Namdarian, 2018.
(plastic box 6.9 x 7.9 x 2+3/8 inches, 39 plastic pieces, directions for 30 problems)
A puzzle box where the lid is a 2-layer sliding piece puzzle, where the top layer pieces may poke into the edges of the box, but must avoid stops that can be placed. Problem 1 is to remove the lid from the shipped puzzle; on the right above is the lid off with all ten stops removed. Below on the left is the bottom layer, and the second diagram is the middle layer with the stops placed as shipped. The half width projections of corner pieces could just as well be full width and still avoid stops (since stops fully block a row), but can in some cases allow a closer fit to the cross (which has angled inside corners to keep out a full 1x1 tile), as shown in the third diagram below, which is also an example of how the cross may also project into the box side. Different problems may have different stops or no stops; for example, the fourth diagram below shows Problem 2 (same start position as Problem 1) that has no stops.



Here are 12 basic steps to solve the first problem in a total of 55 sliding motions, where each motion pushes a line of one or more tiles in a horizontal or vertical direction:

12
3
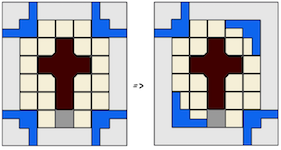
45
6
78
9
1011
12
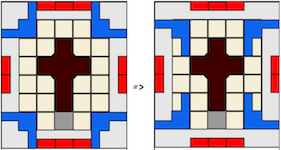
1314
15
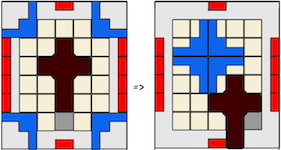
1617
18
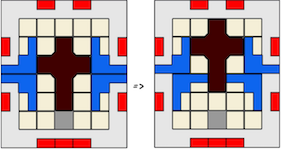
1920
21
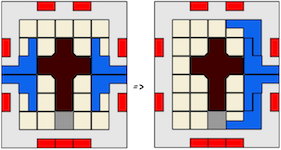
2223
24
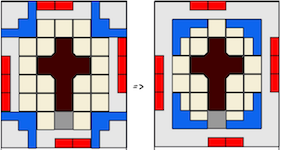
2526
27
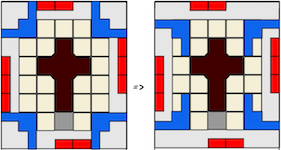
2829
30
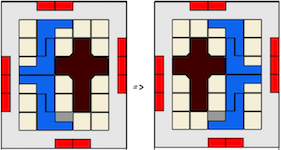

Designed by Tinkercad Modeling.
(Printed on a Monoprice Mini V1 3D printer, from Thingiverse thing 3610958, 2019,
PLA plastic, 2+3/8" high, 2+3/8" wide, 3/8" thick)
Three pieces assemble in a straightforward way to make a heart:

Further Reading
JigsSaw Heart Thingiverse Page,, from: https://www.thingiverse.com/thing:3610958



Chad Valley Co. Ltd., Harborne, England, circa 1920's.
(cardboard box with wood pieces, 5x7 inches;
see also Infants' Hospital Puzzle, Dad's Puzzler - Exchange Version / Infants Hospital, Infants' Hospital - The Magic Line, A Ward Oin The Infants' Hospital,




Old design, this one circa early 1900's?
(wood, 2.25 inches tall, 1.25 inches diameter)
A magic trick, not really a puzzle. J. A. Storer played with this as a child at his grandfather's house in up-state New York.


"Show Boat MONTE CARLO" promotional puzzle, circa 1930's?
(3.6 by 2.25 inch envelope and six cards)

Invented by John Thomas Godfrey, copyright E.S.R. Inc., 1966.
(12" x 14.5" x 1.75" cardboard box, 11.5" high x 12.5" wide plastic board, 15 5/8" marbles)
The first page of the booklet describes how to play the basic game (as well as information about the game and variations such as starting with a different numbers of marbles):Position the top three flippers right, right, left, and position the middle flipper (the "equalizer") to the right.Winning Strategy: Let n denote the current number of marbles waiting to be played, and define:
If you want to go first, position the lowest flipper to the right, and push the trigger in the lower right corner 1, 2, or 3 times to play 1, 2, or 3 marbles.
Then perform these steps for each round of play:The loser is the one who drops the last marble.
- Position the lowest flipper to the left.
- Push the trigger on the lower right once to make Dr. Play, who will then drop 1, 2, or 3 marbles (after done he will leave the lower flipper positioned right.)
- Push the trigger on the lower right 1, 2, or 3 times to play 1,2, or 3 marbles.
state = (n MOD 4) = the remainder when n is divided by 4If Dr. Nim plays when the state = 1, you respond by playing the number of marbles to return the state to 1, and in the final round when only 1 marble is left, he loses. The initial state of 15 marbles is 15 MOD 4 = 3. If Dr. Nim goes first, the position of the center flipper to the right forces him to drop only one marble on the first turn, giving you a chance to play only one marble. Or if you go first, insted of playing just one marble, you can play 2 marbles. Either way, from 13 marbles, continue with a winning strategy that leaves him 9 marbles, then 5, and finally just 1.
The lowest flipper when positioned to the right routes the marble directly to the bottom, but when positioned to the left, routes the marble to the bottom by first rolling over the release lever, which causes another marble to drop.
The booklet calls the center flipper the "equalizer"; once flipped left it stays left. It prevents Dr. Nim from making the correct move of 2 marbles when he goes first (but you can do that if you go first). The booklet says that this is just Dr. Nim being a "true gentleman":
The row of three flippers on the top records the current state of the machine; that is, the current number of marbles MOD 4, which is one of 0, 1, 2, or 3 (the position of the equalizer does not affect state). In the example on the preceding two pages, each step notes the state that remains after that step has completed. For example:
State 0
State 1
State 2
State 3
When the bottom flipper is to the left, and with n marbles waiting to drop, when a marble drops, the state changes from n MOD 4 to (n – 1) MOD 4, and if the resulting state is not 1, the marble is shunted to the right center channel to cause another marble to drop (except when Dr. Nim moves first and the equalizer flipper prevents the marble from making a second marble drop).
Dr. Nim's state transition rule is simple: Each time a marble drops, state 3 goes to state 2, state 2 goes to state 1, state 1 goes to state 0, and state 0 goes to state 3 because:(-1) MOD 4 = (-1 + 0) MOD 4 = (-1 + 4) MOD 4 = (3) MOD 4 = 3When it is his turn, Dr. Nim does not know the current number of marbles. But assuming that the flippers were set correctly at the start (and there have been no mechanical problems like a flipper sticking or two balls dropping at the same time), he always knows the number MOD 4.If it is his turn and state is not 1, he drops the number of marbles to leave a state of 1 (and continue with a winning strategy to win the game).
If it is his turn and state is 1, he drops just one marble, in the hope that you don't know the strategy and make an incorrect decision next round.
Here is the starting position when Dr. Nim goes first:Here is the back of the board. A metal piece folds out so the board will be positioned on a slant, and a long plastic piece along the edge connects the push lever to the ball release:


Wikipedia Page, from: http://en.wikipedia.org/wiki/Dr._Nim
Mad Scientist Page, from: http://www.evilmadscientist.com/2013/dr-nim
Rougetet Article, from: http://hal.archives-ouvertes.fr/hal-01349260/document
Playback Article, from: http://pbgames.wordpress.com/2012/07/08/1940-nimatron
History Computers Article, from: http://history-computer.com/ModernComputer/Relays/Condon.html
Condon Patent, from: www.uspto.gov - patent no. 2,215,54

Games can arguably be viewed as a puzzle to be shared by two or more people ...

Designed by T. Denoul and made by Blue Orange Games 2000.
(Game as purchased had instructions and 3 sets of light and dark 4-nesting cups;
augmented with 5 sets of light and dark top 5-nesting clear cups, J. A. Storer 2005;
wood box and cups where the lid turns over to be the board, 9.5 square)
Board: 4x4 rectangular array.
Pieces: White and black cups ("goblets"), 3 each of 4 different diameters.
Stacks: A stack is a set of one or more nesting cups facing down (largest cup on top).
Start: Board is empty, white and black each have 3 stacks of their cups.
Play: White goes first, players move alternately.A player may move a single cup of their color that is on the board (that may have other cups under it) to an empty square or to cover another stack on the board (of either color).Touch Rule: Players may not touch any stacks with the opponent's color on top, and:
Cups not yet on the board (which must be removed from their stack in order of largest to smallest) may placed on the board in one of two ways: Placed on an empty square.Or, placed to cover an opponents stack that must be positioned in a row, column, or diagonal that contains three opponent stacks.Players may touch a stack on the board with their color on top ONLY when it is their turn, and once touched, that cup MUST be moved to a different square.Win: A player wins when there is a row of 4 stacks (horizontal, vertical, or diagonal) with their color on top; however, if at the end of your turn the opponent has 4 in a row, you lose whether or not you have made 4 in a row.
Draw: The game is a draw if a position is repeated three times.
Goblet Variations
- For a compact travel game, use numbered game chips instead of cups.
- Use cups with white / black tops and clear bodies (so you can see inside a stack).
- Eliminate or modify the touch rule (e.g., top cup can be lifted, but no others).
- Relax the rules for placing a cup that is not yet on the board.
- Start with a different configuration of external stacks (e.g., three stacks of size 5, 4, and 3).
Goblet Moku
- Play on a chess board (ignore the colors of the squares).
- Each player starts with 5 stacks of 5.
- Play is like Goblet, except the 3-in-a-row rule is now a 4-in-a-row rule.
- Win by getting 5 consecutive stacks in a row (horizontally, vertically, or diagonally).
The standard goblet game purchased at the store uses solid pieces so you can't see inside a stack. Clear pieces remove the "memory" component and allow the player to concentrate on the logical component (more fun for some, less for others).
Basic Idea: Cut up different diameters of plastic tubing and plug the tops with dark or light wood. Use clear plastic for clear pieces. Solid pieces can be made with non-clear tubing (hard or impossible to find in small quantity) or by spraying painting clear pieces.
Common types of rigid plastic tubing: Diameters below 1.5" are most common in 1/8" increments with 1/16" thick walls (e.g., 5/8" inside diameter with 3/4" outside diameter).Cast Acrylic: High quality, easy to machine, but may be hard to find in diameters below an inch, and costs more.
Extruded Acrylic: Cheaper than cast, and very clear, but a bit brittle to work with.
Polycarbonate: Similar to the brand name "Lexan". Almost as clear as extruded acrylic, as cheap, a bit more flexible, and a bit less prone to chipping.
CAB: Very cheap, but not as clear (a bit of a yellow tint).
A Set of 5 Goblets:1. 1" long, 1/2" diameter (solid wood).
2. 1+3/8" long, 5/8" I.D., 3/4" O.D., 5/16" thick wood plug in top.
3. 1+3/4" long, 7/8" I.D., 1" O.D., 5/16" thick wood plug in top.
4. 2+1/8" long, 1+1/8" I.D., 1+1/4" O.D., 5/16" thick wood plug in top.
5. 2+1/2" long, 1+3/8" I.D., 1+1/2" O.D., 5/16" thick wood plug in top.

Copyright by xxx, this set made by J. S. Storer 2000.
(11.1" wenge board with 25 cherry 1.2" cubes)
Board and pieces: A 5x5 array of cubes; each cube has an X on one side, an O on the opposite side, and the other four sides are blank.
Starting position: All cubes have a blank side facing up.
Turns: Players X and O alternate moves.
Move: 1. Remove a cube from the outside edge that is blank or has your symbol on it. 2. If the cube is blank, turn it so your symbol is on top. 3. Push the cube back at the other end of the same column or row to cause the cubes in that column or row to slide back into place (so there are two possible moves when a corner cube is removed and three when a side cube is removed):Win: You win when you make a move that causes a row, column, or diagonal to have all five cubes with your symbol on top, with the following two exceptions: 1. If the player fails to announce that 5 in a row has been formed before the opponent moves, it doesn't count (and another move must create 5 in a row before the player can win).
1. If the player fails to announce that 5 in a row has been formed before the opponent moves, it doesn't count (and another move must create 5 in a row before the player can win).
2. If a player causes the opponent to have five in a row, player loses if the opponent announces it.
Further Reading
Similar game in the Obermair Patent, from: www.uspto.gov - patent no. 4,210,337

Copyright by xxx, this set made by J. S. Storer 2000.
(10.5" plexiglass board with wood pieces)
board: A 4 by 4 array of 16 squares.
pieces: Each piece has 4 characteristics: color (light or dark), height (tall or short), shape (square or octagonal ends), texture (smooth ends or hole in the ends).
move: Players move alternately: each move consists of a player selecting a piece and then giving it to the other player to place on an unoccupied square.
win: After placing a piece on the board, a player wins it has formed at least one row of 4 in a row (horizontally, vertically, or diagonally) that are the same for at least one of the four characteristics, and he or she calls "Quarto". If he or she fails to see this, the other player may call Quarto. If both players fail to see a match, then it cannot be used in the future.
variations: Count a 2 by 2 square of pieces with at least on common characteristic a match (so there are 9 more ways to call Quarto). Change the goal to be finding a match with all characteristics different. Require that your move must cause exactly one new match of exactly one characteristic. Etc.

Copyright xxx, this set made by J. A. Storer, 2005.
(x" diameter poker chips glued together; used with a chess board)
Board: An 8 by 8 board (e.g., a chess board where square colors are ignored).
Pieces: 64 identical discs with different colors on opposite sides.
Starting Position:Move: Players move alternately by placing a piece of their color adjacent to a piece of the opponents color (horizontally, vertically, or diagonally) so that at least one outflanking can be performed. An outflanking consists of flipping all all opponent pieces between the piece you placed and another one of your pieces in a given direction (horizontally, vertically, or diagonally). You must move if you can; if no move is possible you forfeit your turn. Once a piece is placed, all pieces that can be flipped, must be flipped. Example: If black places a piece on the square marked x, then three outflankings are performed (one north, one north east, and one east).Win: When it is no longer possible for either player to move, the game ends, and the winner is the one with the largest number of discs showing his or her color.
Example: If black places a piece on the square marked x, then three outflankings are performed (one north, one north east, and one east).Win: When it is no longer possible for either player to move, the game ends, and the winner is the one with the largest number of discs showing his or her color.

a.k.a. Mill, Muhle, Merelles / Merilles, Mulino
Very old game, this set made by J. A. Storer, 1995.
(12.5 by 12.5 by 1/4 inch wood board, 6.75 by 2.25 by 1.5 inch wood box,
1.25 inch white and red poker chips;
king is not used, it is for Tablut on back of board)
Board: Three concentric squares where the midpoints are connected by lines; the intersections are the playing points:Pieces: Nine white and nine black chips.
Play: Players alternately place their chips on a vacant point. When all chips are on the board, the game continues by players alternately moving one of their chips to an adjacent point. Whenever a player forms a row of three chips (horizontal or vertical, but not diagonal), called a mil, an opponent's chip that is not in a mil may be captured (and never returns to the board).
Win: A player wins if the opponent has no legal move or has only two chips left.
--------------------------------
Game variations:
- When not all of a players chips have yet to be placed on the board, the player may choose to make a move instead of placing a chip.
- You may not move a piece to the position it was in the previous turn.
- When capturing, if all of the opponents pieces are in a mil, then any one of them may be captured.
- If two mills are formed by a move, then two opponent pieces may be removed.
- Players may move a chip anywhere when they have only three left.
Five Men's Morris:Each player has 5 chips; don't use the outer ring of the board.Eleven Men's Morris:Each player has 11 chips; add diagonal lines to the board that connect the corners of each ringTwelve Men's Morris:Like 11 Men's Morris but each player gets 12 chips (game is a draw if both players place their all their pieces with out forming mils (filling up all 24 points).
Further reading:
Masters Games Page, from: http://www.mastersgames.com/rules/morris-rules.htm
Bennett's Page, from: http://alumnus.caltech.edu/~leif/games/Morris
Cox-TV Page, from: http://cox-tv.com/games/rules/morris.php
Gamerz Page, from: http://www.gamerz.net/pbmserv/nmm.html
Triad Games Page, from: http://www.tradgames.org.uk/games/Nine-Mens-Morris.htm
BBC Page, from: http://www.bbc.co.uk/dna/h2g2/alabaster/A666209
Classics Technology Center Page, from: http://ablemedia.com/ctcweb/consortium/vamegypt7.html
Gaser Article, from: http://www.msri.org/publications/books/Book29/files/gasser.pdf
Wikipedia Page, from: http://en.wikipedia.org/wiki/Nine_Men's_Morris

Very old game, this set made by J. A. Storer, 1995.
(12.5 by 12.5 by 1/4 inch wood board, 6.75 by 2.25 by 1.5 inch wood box,
1.25 inch white and red poker chips, and a 2.75 inch Chess king;
back of board is a Nine Men's Morris board)
These are the rules described in Murray's History of Board Games:
Pieces: A white King, 8 white pieces, and 16 black pieces.
Board and start position: A 9 by 9 board where the starting position, has the king on the central square, called the Konakis, with eight white pieces surrounding him, and a total of 16 black pieces at the edges:Play: Players move alternately; white moves first. Only the king may move onto the Konakis.
Move: A move consists of moving a piece any number of (unoccupied) squares in the vertical or horizontal direction (i.e., like a rook in Chess).
Capture: A piece is captured and removed from the board when the opponent moves so as to occupy the two adjacent squares in either the horizontal or vertical direction (it is possible to capture up to three pieces on one move. Note that it is the act of moving that causes the capture; a piece may move safely between two opponent pieces.
Win: White wins if the King moves to any square on board perimeter. Black wins if the king is surrounded by black on all four adjacent squares, or on three adjacent squares and the Konakis.
Ludoteka Page, from: http://www.ludoteka.com/tablut-en.html
Wikipedia Page, from: http://en.wikipedia.org/wiki/Tablut
Viking Age Page, from: http://www.vikingage.com/vac/tablut.html
Stmoroky Page, from: http://www.stmoroky.com/GAMES/tablut/tabrules.htm
Passagen Page, from: http://hem.passagen.se/melki9/tablut.htm
Scandinavica Page, from: http://www.scandinavica.com/GAMES/tablut.htm
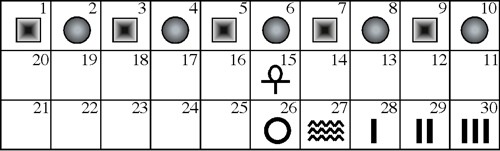
Start: Each player has 5 pieces, initially placed alternating on squares 1 to 10.
Move: Players alternate throwing a set of 4 two sided paddles to move forward:1 white side up = move 1 square and throw againAttack: Landing on an opponent's piece is an "attack", and you exchange places; you may not land on your own pieces.
2 white sides up = move 2 squares
3 white sides up = move 3 squares
4 white sides up = move 4 squares and throw again
4 black sides up = move 6 squares and throw again
Restrictions:Win: You win by removing all of your pieces.
- FIRST MOVE: First throw of the game must move the piece on square 10.
- SAFETY: Squares 15, 26, 28, 29 cannot be attacked.
- DEFENSE: Two or more consecutive opponent pieces cannot be attacked.
- BLOCKADE: Three or more consecutive opponent pieces cannot be passed; however, blockades may not turn corners (10 to 11 or 20 to 21).
- TRAP: Land on 27 and go back to 15 (or the first empty square before it)..
- EXIT: You may not move past 30. A piece on 30 can be removed at the start of your turn if all of your other pieces are out of the first row.
- NO MOVE: If you can't move forward, you must move backward (according to the same rules). If no move is possible your turn ends.
------------------------------
Game variations:
- You must land on square 15 and 26 exactly before moving on.
- 30 is a safety square and/or make up different rules for removing pieces.
- Start with pieces off the board and throw to enter them on to the first row (you cannot land on a square with your piece or one that is part of 2 or more consecutive opponent pieces); count 4 black sides as 5 points, and you can choose to double your throw value.
Senet was played in Egypt over 3,000 years ago. King Tut was buried with 4 Senet boards. The exact rules are not known; scholars have studied old drawings to speculate on the rules.
Rules close to Jequier's Rules have been presented here and are most common (start with 5 pieces each, swap with an opponents piece when you land on it, 2 in a row are safe, 3 in a row are a blockade, etc.). Other proposals for Senet rules include those of Kendall, Tait, and Bell. Kendall has 7 pieces each (starting on squares 1 through 14). Both Bell and Tait start with all of the pieces off the board and throw to enter them on the board. Bell's rules move 10 pieces backwards and winning is by getting them arranged in every other square of the first two rows.
Here are ideas for rule variations, some coming from these other rule sets:
- The game begins by the first player moving from 10 to 11 and then throwing again.
- Designate some or all of squares 15, 26, 28, 29, and 30 as stopping squares, where you must land on them exactly before moving on.
- Different rules for square 27 (e.g., land on square 27 and go back to the lowest numbered empty square, or end your turn and in subsequent turns have to move it before moving another piece).
- Pieces do not have to be out of the first row before you can take a piece off, or alternately, make the lowest square that can have a piece a higher number such as 15 or 21.
- Backward moves may only land on an empty square and / or may pass blockades.
- Limit or eliminate extra throws; can also count 4 blacks as 5 points.
- Start with pieces off the board and move them on according to throws; you can change the rule of an attack to be that it bumps the opponents piece off the board.


Made by J. A Storer, 2005.
(birdseye maple box and wood drawer,
5 rectangular purpleheart pieces, 5 cylindrical plexiglass pieces,
painted mahogany black and white paddles with red handles,
3 x 6 x 15 inches)
Walker's Page, from: http://psion.snigfarp.karoo.net/senet(Includes the rules of Jequier, Kendal, Tait, and Bell.)King Tut House Page, from: http://www.kingtutshop.com/freeinfo/SenetGame.htm
Game Cabinet Page,, from: http://www.gamecabinet.com/history/Senet.html
Humanities Interactive Page, from: http://www.humanities-interactive.org/ancient/tut/senet
Fortune City Page,, from: http://www.fortunecity.com/victorian/lion/193/Senet.html
Master Games Page, from: http://www.mastersgames.com/rules/senet-rules.htm
Terry's Page,, from: http://wesheb.tdonnelly.org/esenet.html
Private Moon Page, from: http://www.privatemoon.com/artists/toys/senet/senet.html
Think Quest Page, from: http://library.thinkquest.org/CR0210200/ancient_egypt/senet.htm
Xmission Page, from: http://www.xmission.com/~psneeley/Shareware/senet.htm
Answers.com Page.pdf, from: http://www.answers.com/topic/senet
SD Museum Of Man Page, from: http://www.museumofman.org/html/lessonplan_senet.pdf
Wikipedia Page, from: http://en.wikipedia.org/wiki/Senet








a.k.a. Nano Backgammon
Invented by J. Pollack, patent applied for, copyright www.nannon.com 2004.
(metal box 2.5 by 3.9 by 3/4 inch, 6 chips, 3 die, board, and directions;
upper set is the 2009 version, lower set is the original 2004 version;
box includes folding board with directions shown above on the back,
and longer directions and information on a double sided 4-panel fould out card)
Pick a set of integers, a set of base integers, and a set of operations, and start your watch to see how many integers you can make from exactly one each of the base integers and the operations. Here are 0 through 50 using the base integers 1, 2, 3, 4 and +, -, *, exponentiation, parentheses:

A variation is to not allow two digits to be placed together to make a two digit number (done above only for some of the numbers 29 or larger); here are some:
A classic problem is to write a program that prints a copy of itself exactly, byte for byte identical (it can be viewed as an abstraction of constructing a machine that manufactures an exact copy of itself). This naive approach is problematic:Make instructions to print the program.The recursion theorem addresses this problem theoretically. In practice, short programs in most any programming language are possible. Here is a short but cryptic self-printing C program:
Add the instructions to print the instructions.
Add the instructions to print the instructions to print the instructions.
etc.In a UNIX terminal window it can be compiled and checked by doing#include; char *x="#include ;%cchar *x=%c%s%c;%cint main(){printf(x,10,34,x,34,10,10);}%c"; int main(){printf(x,10,34,x,34,10,10);} gcc -w; ./a.out > output; diff self.c outputto see that that there are no differences between self.c and output.)
For a practical general approach in your favorite programming language, let START denote whatever is necessary to start a program, and END whatever is needed to end a program. Then a self-printing program could have the form:STARTThis pseudo code essentially prints two versions of the same thing. The first print statement prints the START lines, the for loop prints the lines defining the array, and the second print statement prints the remaining lines.
s[1] := "START"
s[2] := "the remainder of this program after this closing quote"
print s[1]
for i := 1 to 2 do print the string s[i] := ", the string s[i], and the string "
print s[2]
END
To be reasonably readable, START and END may be several lines, making the array s longer, and the two print statements may be for loops to print a number of lines. In pracice, all that may be is needed are assignment statements, for loops, and print statements, where the only significant issue to a particular language may be how to print special characters (quotes inside quotes, etc.).
Read no further!
Write a readable self-printing program in the language of your choice.

*** The text of this program self.c satisfies:
- Fully ANSI compliant and correct. That is, on a UNIX system, no errors or warnings, and no output produced when doing: gcc -ansi -Wall self.c; ./a.out > Output; diff self.c Output
- The only commands used for output are putchar, puts, or printf .
- No additional # statements (does not get any input, does not read or write to a file).
- At most one statement per line.
- No lines have more than 80 characters.
--- 1486 --- Books
 Many books with material on mechanical puzzles have been written over the past century, and before. Two old and well know examples (at the top and the bottom of the pile shown above) are Puzzles Old And New (1893) and Sam Loyd's Cyclopedia Of 5,000 Puzzles, Tricks, and Conundrums (1914).
Many books with material on mechanical puzzles have been written over the past century, and before. Two old and well know examples (at the top and the bottom of the pile shown above) are Puzzles Old And New (1893) and Sam Loyd's Cyclopedia Of 5,000 Puzzles, Tricks, and Conundrums (1914).--- 1487 --- The 1893 Hoffmann Book





Puzzles Old And New
by Professor Hoffmann
pen name for Reverend Angelo John Lewis
(Frederick Warne and Co. London & NY 1893;
7.3 inches by 5.4 inches, hard cover first editions, each 394 pages (scan 1) (scan 2),
some with up to four pages of adds at the end)
The grandfather of puzzle books. It was published in at least the cover colors teal, red, brown, blue, and green, with two different cover styles (the teal and the first of the two reds above are cover style 1, and the others are cover style 2). The books all have identical pages, except that cover style 1 has no date on the title page (although the teal copy above has the inside back binding page signed "M. D. April 24, 1893"), and there are varying numbers of pages of adds at the end. All of the books above, except the teal, have the same light brown patterned end paper inside the covers; the teal has a light green end paper of a different pattern (although the teal version was also made with the same end paper as the others).
The teal and red versions in cover style 1 above both have two pages (one double sided sheet) of adds for magic and puzzles at the end. The red version in cover style 2 above has date 1893 on the title page, and has two pages of adds at the end for conjuring and ventriloquial items. The blue above is like the red except that at the end, preceding the same two pages of adds are two additional pages of adds for other books. The brown and green versions above are just like the red and blue but with no adds at the end.
Each chapter includes solutions. It is interesting to see the variety of puzzles known at this time; Eight Peg ("Four and Four"), the Fifteen Puzzle ("Boss Puzzle"), Cross Keys, 6-Piece Burr ("The Nut"), Chinese Rings ("Cardan's Rings"), Tangram ("Anchor Puzzle"), etc.--- 1488 --- Close Up Views Of The Two Hoffmann Book Cover Styles



--- 1489 --- Hoffmann Books End PaperThe teal book shown on the first page uses the green end paper shown below, and all the others use the brown paper shown below. The teal version was also made with the brown end paper (in fact, the book with brown paper shown below is a different copy of the teal version).


--- 1490 --- Sample Pages From The Hoffmann Book(From the 1893 second cover version.)



--- 1491 --- Sample Pages From The Hoffmann Book Continued







--- 1492 --- Later Editions of the Hoffmann Book
(copyright Frederick Warne and Co. London & NY 1893;
this edition L. E. Hordern and Martin Breese Limited 1988;
7.3 inches by 5.4 inches, hard cover, 394 pages,
each with 2 pages of adds for puzzles at the end;
these adds are the same as the teal first edition shown above)
This 1988 edition has a preface by L. E. Hordern that discusses the books history and gives the authors real name; here is some of what is said on the back of the jacket: "He was able to combine this with a wealth of accurate drawings, from which it must be assumed that he either possessed or had access to the puzzles he was describing. For some 80 years or more (until the advent of modern printing techniques), his book stood alone, head and shoulders above the rest."

(copyright Frederick Warne and Co. London & NY 1893;
this edition Sterling Publishers New Delhi 1997,
7 by 4.75 inches, soft cover, 394 pages,
each with 2 pages of adds for puzzles at the end;
with two contemporary adds at the end for reprints of Hoffmann magic books)
Further reading:
Knuth's index to Hoffmann's book, from: http://sunburn.stanford.edu/~knuth/hoffmann.txt
Puzzle Museum, from: http://puzzlemuseum.com/library/hoffm/hoff-bk.htm--- 1493 --- Hordern's Edition Of The Hoffmann Book

Hoffmann's Puzzles Old And New
by Professor Hoffmann and Edited by L. E. Hordern
(Copyright L. E. Hordern, printed in Great Britain 1993,
8 by 10 inches, 256 pages)
L. E. Hordern has re-set in different type the material from the original 1893 Puzzles Old And New by Prof. Hoffmann (pen name for Reverend Angelo John Lewis), and organized it so the solutions come after the puzzle (instead of at the end of the chapter as in the original book) and photographs of corresponding antique puzzles are intermixed with the pages (e.g., two pages of material from the original book on one page and photographs on the facing page). The original figures are included, but with different numbering, and some but not all errors in the original book have been corrected. Here is text the jacket back:

--- 1494 --- Photos of The Front Matter









--- 1495 --- Het Puzzle-Boek

door Prof. Hoffmann Met 521 teekeningen, circa 1900.
(The Puzzle Book by Prof. Hoffmann With 521 drawings)
(16 pages front matter and 360 pages, 7.5" x 5.4" x 3/4")
A Dutch translation of the 1983 Hoffmann book that has Hoffman chapter 5 omitted ("Word and Letter Puzzles"), so the Hoffmann chapters 6 to 10 are numbered 5 to 9, and there are only 39 problems in chapter 8 (problems 15, 24, 30, 33, 37, 39 of Hoffmann Chapter 9 omitted).--- 1496 --- Hoffmann Posthumous Booksby Professor Hoffmann
pen name for Reverend Angelo John Lewis
(Frederick Warne and Co. London & NY,
undated first editions circa 1925;
each 7.1 inches by 4.9 inches, semi-soft cover)
These three books were published in the 1920's frame, after Professor Hoffmann's death in 1919. Each presents a portion of the original 1893 Puzzles Old And New:
--- 1497 --- Hoffmann's Best Math Book

Professor Hoffmann's Best Math and Logic Puzzles
by Louis Hoffmann
pen name for Reverend Angelo John Lewis
(Dover Publications 2007,
8.5 inches by 5.3 inches, soft cover, 158 pages)
A collection of math and logic puzzles from the 1893 Hoffmann book, Puzzles Old and New.--- 1498 --- Hoffmann Patience Games Book


The Illustrated Book Of Patience Games
Translated and edited by Professor Hoffmann
(Copyright George Routledge & Sons, London 1892,
123 pages hard cover, 8+3/8" x 6+1/8" x 7/8";
a book of solitaire card games by the same author of the classic Hoffman book of puzzles.)--- 1499 --- Hoffmann's Magic Trilogy Booksby Professor Hoffmann
pen name for Reverend Angelo John Lewis

Modern Magic
(David McKay Co., Philadelphia, PA, undated circa 1910, 8 by 6 inches, 563 pages)

More Magic
(David McKay Co., Philadelphia, PA,
undated, circa 1920, 7.9" x 5.75", 457 pages)
Later Magic
(undated, circa 1920)
Called the "Magic Trilogy" in the Findlay and Sawyer book, unlike the 1893 Hoffmann book, they are about magic (but also fun reading for puzzle enthusiasts). Modern Magic is the most published of the three on the left below is the dust cover from a circa 1920's edition and on the right the cover of a 1978 soft-cover edition:


--- 1500 --- Hoffmann Study Book

Professor Hoffmann: A Study
by J. B. Findlay and T. A. Sawyer
(Copyringht Thomas Sawyer 1977,
8.75 inches by 5.8 inches, hard cover, plastic dust jacket, 67 pages,
number 470 of 500 copies printed)
This book focuses on Hoffman's magic books, featuring what he refers to as Hoffmann's magic trilogy, and catalogs the many publications of Hoffmann's books, including Hoffmann's Puzzles Old and New. Puzzles Old and New. The inside covers have reproductions of hand written documents by Hoffmann, and included with the book is a reproduction of a 1881 "Monday Evening Entertainment" flyer featuring Hoffmann. Shown above is the cover and the text from inside the jacket.--- 1501 --- Robert Merry's Books Of Puzzles 1-3
No mechanical puzzles, but fun reading; here is a sample page (from the third book):

Further Reading
Merry's Rhymes and Puzzles pdf, from: http://www.archive.org/details/merrysbookofpuzz00stea--- 1502 --- Merry's Arlington Edition

Hurst and Co., Publishers, NY, circa 1880's.
(hard cover, 7.6" x 5.3" x 1", 300 pages;
hand written on a blank page inside the cover "Merry Christmas from Mamma 1887")--- 1503 --- Excursions Into Puzzledom

By The Late Tom Hood and His Sister,
Strahan And Company Limited, 34 Paternoster Row, London, 1879.
(hard cover, 7.8" x 5.6" x 1", 420 pages with 4 pages of adds at the end)
No mechanical puzzles, but many word problems that make fun reading; here is a sample page:

--- 1504 --- Everybody's Puzzle Book
Everybody's Illustrated Book of Puzzles
(Saxon & Co. Publishers, London, 1890 first edition,
8.75 by 6 inches, 125 pages with three pages of adds at the end)
Below left is the back cover, and right a circa 2008 paperback edition (Kessinger Publishing, 9 by 6 inches, reproduces title page, 125 pages, and the first two pages of the adds at the end).


Further Reading
Scans of the pages, from: http://www.archive.org/stream/everybodysillust00lemoiala
Text of the pages, from: http://www.archive.org/stream/everybodysillust00lemoiala--- 1505 --- Richter Company U.S. Brochure

F. Ad. Richter & Co., American Office, NY, New York.
(soft cover, 8.2" by 5.8", 18 pages)--- 1506 --- Front & Back CoverFront Cover Inside and Page 1

--- 1507 --- Pages 2 - 3Pages 4 - 5

--- 1508 --- Pages 6 - 7Pages 8 - 9

--- 1509 --- Pages 10 - 11Pages 12 - 13

--- 1510 --- Pages 14a - 14bPages 15a - 15b

--- 1511 --- Pages Pages 16 - Inside Of Back Cover
--- 1512 --- New Book Of 200 Puzzles

Wehman Brothers, 126 Park Row, NY, NY, Copyright 1908.
(soft cover, 4.9" x 3.8" x 3/16", 58 pages with 4 pages of adds at the end;
book back advertises other books in the series)
Describes a variety of puzzles, including mechanical puzzles such as 2D packing puzzles, Moving Rings (page 9, "string and Balls") and a 6-piece burr (pages 40-41, "Chinese Cross").
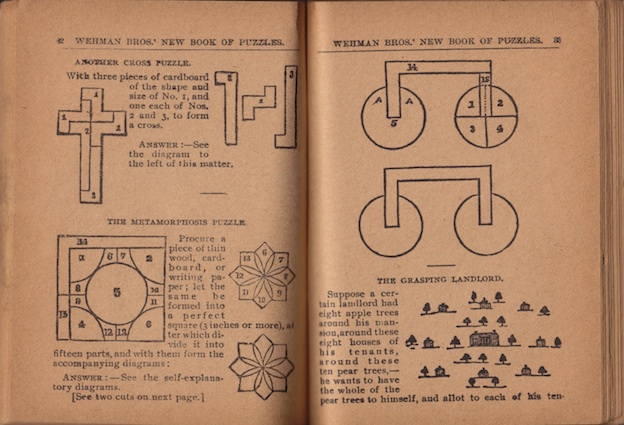
--- 1513 --- Dudeney 1920's BooksDudeney (who lived in England 1847-1930) is famous designer of mathematical puzzles. These books have overlapping content and have been published in many editions. Although the main focus is mathematical puzzles, there is significant material relating to mechanical puzzles and mechanical puzzle design (2-dimensional geometry, broken chessboard, Fifteen puzzle, etc.).
Further reading:
Knuth Strand index, from: http://sunburn.stanford.edu/~knuth/dudeney-strand.txt
Kunth Weekley Dispatch Index, from: http://sunburn.stanford.edu/~knuth/dudeney-twd.txt
Project Gutenberg Text of Dudeney AIM, from: http://www.gutenberg.org/files/16713/16713.txt
Math Forum Dudeney CP, from: http://www.mymathforum.com/books/thecanterburypuzzles--- 1514 --- Dudeney Posthumous Books--- 1515 --- Sam Loyd's 1914 Cyclopedia Of Puzzles

Sam Loyd's Cyclopedia of 500 Puzzles, Tricks & Conundrums With Answers
by Sam Loyd
(left: "FRANKLIN BIGELOW CORPORATION, THE MORNINGSIDE PRESS PUBLISHERS";
right: "LAMB PUBLISHING COMPANY";
both NY, 1914, 11.5" by 8.5" by 1.5", hard cover, 384 pages;
volumes are identical except for the publisher listed on spine and title page;
the black on the spine edges on the right is from a professional repair in 2008)


(2007 edition by Ishi Press International with an Introduction by Sam Sloan,
10.5 inches by 8 inches, soft cover, 384 pages)
A classic book of puzzles of the famous Sam Loyd, compiled by his son after his death (Loyd lived from 1841 to 1911). Although the bulk of this book is devoted to mathematical puzzles, it is fun reading and there is material relating to mechanical puzzles. For example, the Towers of Hanoi puzzle is presented on page 223, and the Fifteen puzzle is presented on page 235.
Further reading:
Knuth's index to Loyd's book, from: http://sunburn.stanford.edu/%7Eknuth/loyd-cyc.txt
Cyclopedia pages or pdf, from Pegg's Math Puzzles Page: http://www.mathpuzzle.com/downloads--- 1516 --- Sam Loyd and His Puzzles



Copyright Barse & Co., New York and Newark NJ, 1928.
(hard cover, 8.75" x 6.7" x 5/8", 122 pages)
Above are shown the table of contents, the preface, and a sample page (page 40). Pages 1 to 4 discuss the Fifteen puzzle and its (at that time) recent popularity. Various puzzles are described on pages 5 to 22, pages 23 to 86 present a selection of Loyd puzzles (essentially a subset of the Loyd Cyclopedia), and pages 87 to 119 give solutions. Pages 120 to 122 are the index.--- 1517 --- Wyatt's 1928 and 1946 Books
These books are a nice early presentation of wood puzzles and their construction, including the Missing T ("Cut-Up T"), Tangram ("Cut-Up Square), a version of Iribako ("Bewitching Cubes"), Fifteen ("Shuffle Puzzle 1"), Dad's Puzzler ("Shuffle Puzzle 2"), a version of the Checkerboard Puzzle, ("Cut-Up Checkerboard), Towers of Hanoi Towers Of Hanoi ("Peg And Disc Puzzle"), Wood Knot ("Three Piece Cross"), simple 6-Piece Burrs, and a number of other burrs. Both books have been printed many times (when Wonders in Wood was published, Puzzles in Wood was in its eighth printing); here are 2007 editions:




Puzzles In Wood and Wonders In Wood by E. M. Wyatt (left: Fox Chapel Publishing 2007, 8.4 by 5.5 inches, paperback, 64 pages;
right: Linden Publishing Co. 2007, 9 by 6 inches, paperback, 76 pages)--- 1518 --- 1929 Johnson Smith Catalog
1929 Johnson Smith & Co. Catalogue
Edited by Tony Goodstone, Introduction by Jean Shepherd
(Chelsea House Publishers, NY & London, 1970
9.5 inches by 6.5 inches, hard cover with box, 768 pages)
A re-printing of the 1929 Johnson Smith & Co. Catalogue of "surprising novelties, puzzles, tricks, jokegoods, useful articles, etc.". Everything from guns to whoopee cushions. Page 754 shows wood puzzles including a 6-piece burr and burr stick. Like the Visual History of the S.S. Adams Co., this book is fun reading about a time past. Here are the two sides of the box:


--- 1519 --- Hirschberg's 1930 Book
Can You Solve It?
A book of Puzzles And Problems
by Arthur Hirschberg
(Hutchinson and Co., London, undated first edition,
7.6 inches by 5.25 inches, hard cover, 288 pages;
handwritten inside the cover is
"Harold Frankland, Xmas, 1930",
and on the back side of the title page it says:
"Made and Printed in Great Britain
The Gainsbourough Press, St. Albans.
Fisher, Knight & Co., Ltd.")
Mainly mathematical puzzles, but it is fun reading with solutions for all problems. There is some material relating to mechanical puzzles. For example, Problem 824 is a smaller 6-peg version of the classic Eight Peg puzzle.--- 1520 --- I-X-L Puzzle Book
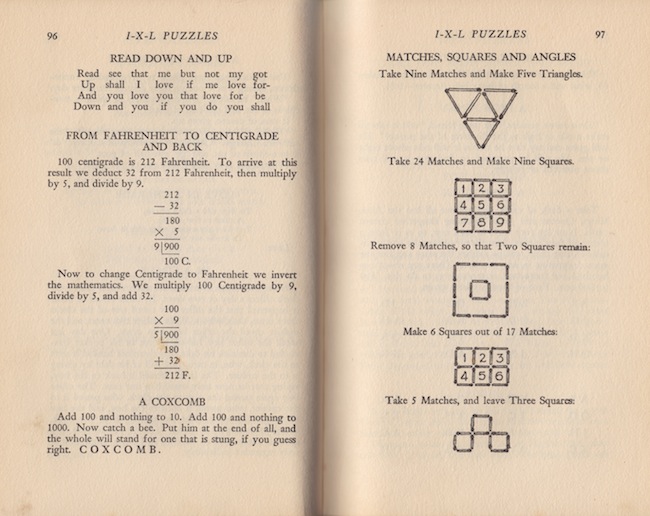
Copyright Henry A. Whit 1938,
Hammond Press, W. B. Conkey Company, Chicago.
(hard cover, 7.5" x 5.25" x 1", 224 Pages;
an assortment of word and math puzzles, many presented with a solution;
sample pages shown above)--- 1521 --- The 1942 Filipiak Book




100 Puzzles How To Make And Solve Them
& Mathematical Puzzles And Other Brain Twisters
by Anthony S. Filipiak
(left: copyright A. S. Barns and Co. 1942, 8.25" x 5.3", hard cover;
middle: copyright Bell Publishing Co. with A. S. Barns Co. 1942, 8.2"x5.8", hard cover;
right: copyright Bell Publishing Co. with A. S. Barns Co. 1942, 1978 printing, 8.2"x5.8", hard cover;
these two bindings of this book have the same 120 pages,
the second has a jacket - the inside of the covers shown above)
A glimpse into 1940 puzzle technology, including sliding piece puzzles and burrs.--- 1522 --- Everythings A Puzzle

Copyright Unicorn Books Inc. 1953, no author listed.
(hard cover, 8.25" x 5.6" x 3/4", 184 pages)
No mechanical puzzles, but many word problems that make fun reading. Begins with 181 pages of "Rebus Puzzles" (sample page below) followed by other word puzzles and quizzes.

--- 1523 --- Bell's History of Board Games

Board and Table Games From Many Civilizations
by R. C. Bell
(Oxford Univerty Press 1960, 1969,
this edition copyright R. C. Bell and Dover Publications 1979,
8.4 inches by 5.4 inches, soft cover, 155 pages)
Presents classic and antique board games (nine men's morris, tablut, etc.).--- 1524 --- Murray's History of Board Games


A History of Board Games Other Than Chess
by H. J. R. Murray
(Hacker Art Books 1978,
9.5 inches by 6.5 inches, hard cover, 267 pages)
Presents classic and antique board games (nine men's morris, tablut, senet, etc.).--- 1525 --- Delft And Botermans Book

Creative Puzzles of the World
Peter Delft and Jack Botermans
(hard cover, 200 pages, Copyright 1978 Harry N. Abrams Inc. NY, NY)--- 1526 --- Winning Ways Books



Winning Ways Volumes 1 and 2
by Elwyn R. Berlekamp, John H. Conway, and Richard K. Guy
(Academic Press 1982, 9.5"x7.25", soft bound, 850 pages total)
A classic two volume study of the mathematics of games, including sliding piece puzzles.--- 1527 --- Hordern's Sliding Puzzle Book

Sliding Piece Puzzles
by L. Edward Hordern
(Oxford University Press 1986,
8.75 inches by 5.75 inches, hard cover, 249 pages)
The quintessential book on sliding block puzzles, including a large appendix of puzzle solutions (Dad's Puzzler, Ma's Puzzle, Neo Black and White, Trap, etc.).--- 1528 --- Slocum and Botermans Books



Puzzles Old & New How to Make and Solve Them
by Jerry Slocum and Jack Botermans
(Plenary Publications 1986,1987, Distributed by U. Washington Press,
10.5 inches by 9 inches, 1986 hardcover & 1987 soft cover, 128 pages)


New Book Of Puzzles 101 Classic and Modern Puzzles to Make and Solve
by Jerry Slocum and Jack Botermans
(W. H. Freeman 1992, 10.4" by 9.4", hard cover, 128 pages)


The Book Of Ingenious Diabolical Puzzles
by Jerry Slocum and Jack Botermans
(Times Books / Random House 1994, 11.1" x 8.75", hard cover, 152 pages)--- 1529 --- Cutler's 6-Piece Burr Books
These two books are the definitive analysis of the standard 6-piece burr. The complete analysis of the 35,657,131,235 possible standard 6-piece burrs that are described was a triumph of computer programming and the power of limited computing resources at that time. With his definition of level (the number of moves to remove the first piece, where consecutive movement of pieces in the same direction counts as a single move), Cutler discovered many interesting facts about the standard 6-piece burr, including a maximum level of 12 (one of the assemblies of Love's Dozen, that there are none of level 11, a number of unique level 10 standard 6-piece burrs (e.g. Computer's Choice Unique 10), and that 5 is the highest level for a standard 6-piece notchable burr with a unique solution (e.g., L5 Notchable). He also found the Programmer's Nightmare that has 102 assemblies where only one can be taken apart, and it requires a legal twist move. These books were followed later by other computer analyses of Cutler's, including of a class of 3-piece burrs (yielding the terrific Gigaburr and Gigaburr-2 puzzles).--- 1530 --- The Mathematics Of Games
by John D. Beasley
(Copyright Oxford University Press, 1989,
8.75 inches by 5.7 inches, hard cover with jacket, 169 pages)
Presents a fun range of topics in game theroy, including material on Rubik's Cube.--- 1531 --- Coffin's Book On Polyhedral DissectionsThe Puzzling World of Polyhedral Dissections




by Stewart T. Coffin
(Oxford U. Press 1990, 8.75" x 5.75", hard cover, 196 pages, signed by the author)


Geometric Puzzle Design
by Stewart T. Coffin
(A. K. Peters 2007, 9 inches by 6 inches, soft cover, 204 pages)
Many of the classic designs of one of the great designers of these type of puzzles. The second book is basically a revised edition of the first, which was published on CD and then made available in 1998 at: http://www.johnrausch.com/PuzzlingWorld/default.htm--- 1532 --- Coffin's Puzzle Craft Books



Puzzle Craft
by Stewart Coffin
(published by Stewart Coffin 1985 - 100 pages and 1992 - 80 pages, soft cover)
The 1992 edition used the same cover as the 1985 edition; the inside of this cover is shown above, along with the prefaces to both editions. These are predecessors to the Oxford U. Press Coffin book, and electronic versions are available on the CD version of that book.--- 1533 --- The Puzzle Archade
The Puzzle Archade
by Jerry Slocum
(Klutz Inc., 1996,
8 inches by 8.75 inches, soft cover ring binding with attached pouch, 48 pages)
A puzzle activities book; here is a view of the back:

--- 1534 --- Gabarchuk's Sliding Block Puzzle Book
Neo Sliding Block Puzzles
by Sehiy Gabarchuk (Copyright 1996, self published, 11.7 inches by 8.3 inches, soft cover, 47 pages)
Page 3 is an introduction, pages 4 - 33 present some of the Gabarchuk puzzles, and pages 35 - 47 present solutions.--- 1535 --- Frederickson's Dissections Book

Dissections Plane & Fancy
by Greg N. Frederickson
(Copyright Cambridge University Press 1997,
9.5 inches by 7.25 inches, hard cover with jacket, 310 pages)
A study of geometric dissections and some of the theory that can be used in geometric puzzle design. A great academic work with a good bibliography. On the back of the jacket a quote from Martin Gardner:"Cutting a geometrical figure into the smallest number of pieces that will rearrange to make a different figure is one of the most elegant and surprising branches of recreational mathematics. No one knows more about this, or is more skilled at breaking old records, than Greg Frederickson. His book will be a classic."--- 1536 --- G4G Tributes To Martin Gardner

The Mathemagician and Pied Puzzler
Elwyn Berlekamp and Tom Rodgers, Editors
(A. K. Peters 1999, 9.25 inches by 6.25 inches, hard cover, 266 pages)


The Puzzlers' Tribute, A Feast For The Mind
David Wolf and Tom Rodgers, Editors
(A. K. Peters 2002, 9.25 inches by 6.25 inches, hard cover, 420 pages)
These books have contributions by participants in the first four "Gatherings for Gardner" (G4G) to honor Martin Gardner (who had the mathematical Games Section in Scientific American for many years starting in 1957). They contain recreational mathematics, including things like sliding piece puzzles and burrs.--- 1537 --- The Follette Puzzle Design Book

New Wood Puzzle Designs
by James W. Follette
(Linden Publishing Co. 2001,
11 by 8.5 inches, soft cover, 96 pages)
Wood puzzle designs include Soma Cube, Pentominoes, Towers Of Hanoi, some string puzzles, and some novelty puzzles.--- 1538 --- Frederickson BooksFollowing on his terrific 1997 book on dissections, here are three more books:


Hinged Dissections: Swinging & Twisting , by Greg N. Frederickson
Cambridge University Press, 2002 (hardcover).


Piano-hinged Dissections: Time to Fold! , by Greg N. Frederickson
A K Peters, 2006 (hardcover, with video on an accompanying CD).


Ernest Irving Freese's Geometric Transformations:
The Man, the Manuscript, the Magnificent Dissections!
by Greg N. Frederickson
World Scientific, 2017 (soft cover; was also sold in hardcover and ebook)--- 1539 --- The Tangram Book

The Tangram Book
by Jerry Slocum
(Sterling Publishing Co. 2003, 10.25 inches by 8.4 inches, hard cover, 192 pages)
A history of this puzzle with photographs of antique ones (including an old Chinese Tangram table set) and diagrams of the many figures that can be made; also published in soft cover:


(Sterling Publishing Co. 2004, 10 inches by 8 inches, soft cover, 192 pages)--- 1540 --- Haubrich's Checkerboard Puzzles

--- 1541 --- The Fifteen Book

The Fifteen Puzzle
by Jerry Slocum and Dic Sonneveld
(published by the Slocum Puzzle Foundation 2006,
10 inches by 8.5 inches, hard cover, 144 pages)
Presents a history of the Fifteen puzzle starting with its high popularity in the 1880's, and includes many photos of antique puzzles.--- 1542 --- A Visual History of The S.S. Adams Co.

Life of The Party
A Visual History of the S. S. Adams Company
Makers of Pranks & Magic For 100 Years
by Kirk Demarais with forward by Chris Ware
(published by S. S. Adams LLC 2006,
12.5 inches by 9.25 inches, hard cover, 198 pages)
Presents a visual history of the S. S. Adams Co. with many photos of products from the Company's 100 year history, including some puzzles. Like the 1929 Johnson Smith Catalog, this is fun reading about a time past.--- 1543 --- The SelfLensch Puzzle Design Book

Wood Logic Puzzles
by James W. Self and Tom Lensch
(Creative Publishing International 2006,
10.8 by 8.25 inches, 126 pages + 1 page adds at end)
Wood puzzle designs include Soma Cube, Half Hour Puzzle, Wood Knot, Towers of Hanoi, and a six piece burr,--- 1544 --- Boardman's Puzzle Projects Book

Puzzle Projects for Woodworkers
by R. C. Boardman
(Linden Publishing Co., 2007, 11 inches by 8.4 inches, soft cover, 95 pages)
A collection of wood puzzle projects, including Blockhead, L5 Notchable Six Piece Burr, and Pandora's Box. Project descriptions include photos, drawings, and solutions.--- 1545 --- The Cube Book

Copyright 2009 Jerry Slocum, Black Dog & Leventhal Publishers.
(soft cover, 8.5" x 8" x 3/8", 142 pages)--- 1546 --- Hess Mathlete Book

All-Star Mathlete Puzzles
by Dick Hess
(Copyright 2009 Sterling Publishing Co., NY;
soft cover, 94 pages, 8.2" x 5.5" x 5/16" thick)--- 1547 --- Diaconis and Graham Book

Magical Mathematics
by Persi Diaconis and Ron Graham
(with Forward by Martin Gardner, Princeton University Press 2012;
9.75" x 8.9" x 3/4", hard cover with jacket, 244 pages)--- 1548 --- Stickman Book

Copyright Robert Yarger; edited by Matthew Dawson 2012.
(softcover book in 9" x 11" x 7/8" puzzle frame)
A catalog of the "Stickman" puzzles designed and made by Robert Yarger, that commemorates the 25th numbered design and 1000th puzzle made. It includes a 5 page history of the Stickman puzzles followed by descriptions of the puzzles, and ending with solution summaries and a table of puzzles produced. The frame around the book is a puzzle itself, which is shown below coming apart (a limited Milestone Edition came with a complex puzzle frame around this frame):

--- 1549 --- Table Of Puzzles Produced Shown On The Last Page
--- 1550 --- The Anchor Puzzle Book
The Anchor Puzzle Book by Jerrry Slocum and Dieter Gebhardt
(hard cover, 152 pages, June 2012)--- 1551 --- Information On the Anchor Puzzle Book Provided By The Publisher
--- 1552 --- Coffin's AP-ART Book
AP-ART
A Compendium Of Geometric Puzzles
by Stewart Coffin
(published by Stewart Coffin 2014 - 228 pages, 11.5" x 8.5" x 9/16")
Loose pages for inclusion in a notebook, of nice color photographs with descriptions, presented in order of the author's revised numbering system, presenting the many geometric wood puzzles he has designed. There is no index; below is the table of contents (there are no page numbers, but they are indicated here in parentheses):Part 1: The Plan (pages 7 - 8)
Part 2: Background (pages 9 - 18)
Part 3: Puzzles in Wood (pages 19 - 174)
Part 4: AP-ART Models (pages 175 - 182)
Appendix A: Polyhedral Building Blocks (pages 183 - 186)
Appendix B: Square Root Type Puzzles (pages 187 - 190)
Appendix C: Interlocking Puzzles (pages 191 - 192)
Appendix D: Polly's Flagstones (pages 193 - 194)
Appendix F: Psychogeometrics (pages 195 - 196)
Appendix F: Rhombticks (pages 197 - 200)
Appendix G: Glossary (pages 201 - 202)
Appendix H: Additional Resources (pages 203 - 204)
Appendix I: Parting Shot (pages 205 - 208)
Appendix J: Old Serial List (pages 209 - 210)
Appendix K: New Serial List (pages 211 - 228)Thumbnail Index
857 TOC entries, for a total of 1463 items (1362 puzzles, 9 games, and 92 books)